单齿破碎参数对水合物切削力影响规律研究❋

王 凡， 王国荣,3,4❋❋， 张亦弛， 李清平钟 林,3,4， 贺湘伟

(1.西南石油大学机电工程学院，四川 成都 610500； 2.西南石油大学 能源装备研究院，四川 成都 610500；3．西南石油大学 石油天然气装备教育部重点实验室，四川 成都 610500；4. 西南石油大学 油气藏地质及开发工程国家重点实验室，四川 成都 610500；5.中海油研究总院有限责任公司，北京 100028；6.株洲时代新材料科技股份有限公司，湖南 株洲 412000)

天然气水合物是一种高密度、高热量、可替代化石能源的理想清洁能源，也被称为“可燃冰”[1]。目前国际上也实现了利用降压法、加热法、置换法或以上几种方法的联合进行试采[2]。但是由于水合物具有埋藏浅、弱胶结等特点，且大部分不具有完整的存储形态，而上述方法更适用于具有一定封闭盖层的水合物的试采。因此周守为等[3]提出了针对于表浅层水合物开采的深水浅层海洋水合物固体流化开采技术，主要通过对水合物进行破碎采掘后密闭运送至水面支持系统，使其变成安全可控的天然气水合物资源。

欧阳义平等[4]利用SPH法建立单齿三维仿真模型，验证了西松裕基于剪切破坏提出的单齿切削力计算模型[5]，同时基于自行创建的单齿切削力估算模型，构造了整个绞吸头轴向力，切向力，法向力的计算模型[6]。伍开松等[7]通过建立破岩效果指标函数，利用ABAQUS进行了PDC单齿破碎水合物的参数优选研究。徐海良等[8-10]通过有限元进行了绞吸式水合物开采的绞吸能力、绞吸头受力和绞吸功率的研究。

虽然已有大量数值方法来仿真研究单齿切削破岩和绞吸头破碎水合物，但均未对影响切削载荷的绞吸式单齿破碎参数以及它们对切削载荷的关系做详细探讨。因此本文利用基于相似原理的水合物替代样进行了矩形齿单齿正交破碎实验，研究了不同几何参数在不同切削深度对刀齿切向力、法向力之间的影响；并基于D-P准则建立了三维单齿正交切削的切向力和法向力解析式，利用实验数据对有限元模拟进行验证，以此开展模拟正交实验，分析各因素对切削比能的影响比重，优选出最佳刀齿几何参数。

1 单齿破碎实验方案

本文采用相似材料法[11]制配水合物替代样，其物性参数均为相关研究[12-16]的中间值。其物性参数如表1所示。采用控制变量法研究前角、刀齿宽度在不同切削深度下对平均切向力FC、平均法向力FN的影响规律。实验采用牛头刨床改装的“单齿线型岩石切削实验台架”，通过电压式三项传感器采集切向力与法向力。切削速度为0.3 m/s，方向与切削刃垂直，后角为5°。研究前角在不同切削深度下对切削力的影响时，刀齿宽度保持20 mm；研究刀齿宽度在不同切削深度下对切削力的影响时，前角保持45°，其破碎参数如表2所示。

表1 水合物替代样的力学参数 Table 1 Mechanical parameters of hydrate substitutes

表2 破碎参数表Table 2 Fragmentation parameter

2 三维解析模型

采用正八面体上的正应力σoct和剪应力τoct表示D-P准则[17]，取被切削块为独立研究对象如图1。其中AA′B′B为剪切面，面ABC和面A′B′C′为剪切侧面，面BB′C′C为被切削带与切削齿前面的接触表面。

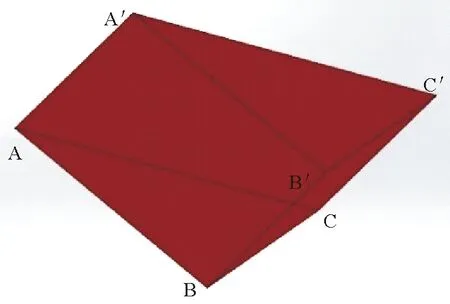
图1 被切削块模型Fig.1 Cut block model

对切削过程作出以下假设：

(1)剪切面AA′B′B和剪切侧面ABC和A′B′C′上的失效符合D-P强度准则。

(2)前切面沿与切削平面成ψ角的平面方向发展成自由平面。

2.1 剪切面上的切削力

切削过程中，剪切面AA/B/B和剪切侧面ABC、A′B′C′上的剪应力τ达到临界剪应力τs时，发生失效破碎。剪切面AA`B`B主要受法向力Fsn和剪切力Fss，刀齿前面主要受法向力Ftn和摩擦力Ftf，如图2所示。

图2 剪切面上的受力情况Fig. 2 Stress on the shear plane

正交切削过程切削速度保持恒定，故根据静力平衡建立如下等式

(1)

其中:χ=π/2+ξ-φ-α;ξ为摩擦角。由于Fss和Fsn位于剪切面上所以满足D-P准则，即

Fss=τoctSs=
τ0Ss+mσoctSs=
τ0Ss+mFns。

(2)

其中Ss为剪切面AA`B`B面积，易知Ss=dW/sinφ。联立1式和2式可解，其中Fn1和Fc1分别为Ft分解至切削方向和竖直方向的力。

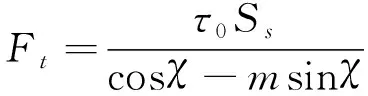
(3)

2.2 剪切侧面上的切削力

剪切侧面ABC、A′B′C′上的剪应力合力Fls和正应力合力Fln同样满足D-P强度准，即

Fls=2τoctSl=2τ0Sl+2mσoctSl。

(4)

其中剪切侧面ABC、A′B′C′面积均为Sl=d2(cotφ+tanα)/2。将剪切面AA`B`B和剪切侧面ABC、A′B′C′上的力进行合成，能够得到刀齿的切向力Fc和法向力Fn。

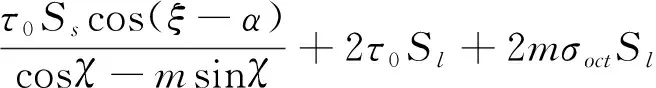
(5)

3 单齿破碎仿真分析

岩石切削过程是一个非线性计算过程，因此本文选用ABAQUS进行搭建模型、调整，并以实验数据进行验证，最后进行正交模拟实验，判断切削深度、刀齿宽度和前角对切削比能的影响顺序，优选出最佳组合。

为方便开展正交模拟实验，对该问题作出如下假设：

(1)单齿的强度和硬度远高于水合物替代样，切削过程中刀齿不发生形变与磨损。

(2)切削过程的切屑对后续切削过程不产生影响。

(3)将水合物看做连续、均质、各项同性材料，忽略温度对水合物的影响。

(4)水合物模型周围以及底部为远场部分。

几何模型采用对称建模；采用线弹、D-P准则、剪切损伤建立材料模型；单元集合的面接触为接触模型；刀齿视为刚体，施加0.3 m/s速度，替代样一侧施加对称载荷，另一侧完全固定，如图3所示。

图3 有限元计算模型Fig. 3 Finite element model

3.1 仿真正交实验方案

结合实际工况与单齿破碎实验数据结论，切削深度舍去2 mm情况。选取L16(45)正交表。正交实验方案如表3、4所示。

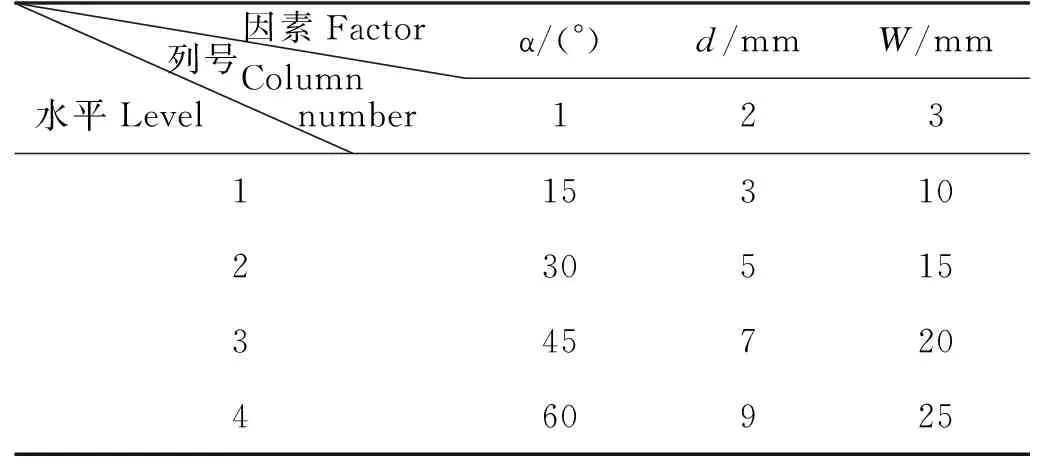
表3 正交模拟实验水平表Table 3 Level of orthogonal simulation experiment

表4 L16(45)正交模拟实验表Table 4 L16(45) Orthogonal simulation experiment

4 结果与讨论

4.1 实验结果与讨论

4.1.1 刀齿宽度对平均载荷的影响 如图4整体而言，切向力、法向力与刀具宽度呈正相关的关系。因为替代样与真实水合物一样存在许多空隙和裂纹。所以当W≤15 mm时，切削载荷受裂隙因素主导，而随刀齿宽度增加的变化趋势并不明显。当W>15 mm时，单位时间破碎量更大，裂纹对平均切削载荷的影响减小，刀齿宽度对平均切削载荷的影响增大。从式5中可得出切向力、法向力与刀齿宽度呈线性关系，基本与图4中各曲线在W>15 mm时的趋势一致。

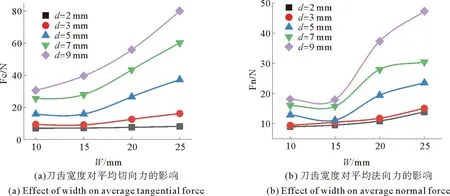
图4 刀齿宽度对平均载荷的影响Fig.4 Effect of tooth width on average load

4.1.2 切削深度对平均载荷的影响 如图5所示，平均切向力与切削深度呈正相关的关系，且随着切削深度的增加，斜率逐渐增大，切削深度的影响更加剧烈。当d≤3 mm时，平均法向力变化随切削深度变化的趋势不明显；当d>3mm时，平均载荷随着切削深度急剧增加，且随刀齿宽度增大，变化更加剧烈。从式5中可看出法向力与切削深度呈一次函数关系，与图5中(b)各曲线在d>3 mm趋势基本一致

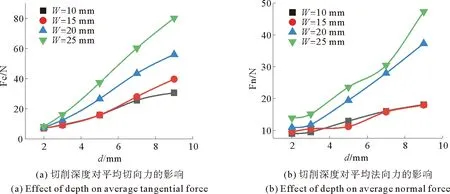
图5 切削深度对平均载荷的影响Fig. 5 Effect of cutting depth on average load

4.1.3 前角对平均载荷的影响 根据岩石切削理论，前角决定着岩石破碎由剪切还是由拉伸主导。如图6所示，随着前角的增加，拉伸破碎逐渐成为替代样切削的主导性机理，切削载荷逐渐下降，呈负相关，与岩石破碎的规律[18]相一致。且随着切削深度的增加，前角对切削载荷的影响逐渐减小。

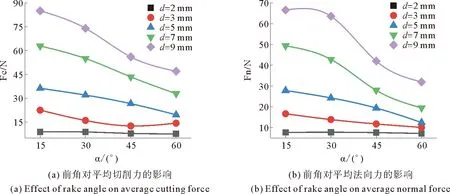
图6 前角对平均载荷的影响Fig. 6 Effect of rake angle on average load

4.2 仿真模型的验证

本文选择α=45°、W=25mm和α=60°、W=20 mm两组刀齿在不同切削深度下的实验数据与模拟实验数据进行对比验证。其中由于模拟采用对称建模，实验数据全部取相应真实数据的一半。

单齿破碎实验数据与模拟实验的对比如图7所示。模拟载荷与切削深度呈现出正相关关系，与实验规律与解析模型规律一致。在α=45°、W=25 mm的情况下，模拟切向力随切削深度的增加与实验值更加接近，分析原因为模拟中的替代样不能表示出真实替代样的空隙，因此在较小切削深度下，实验值比模拟值偏小。但误差都在25%以内，认定在d≥3 mm的工况下，该数值模拟能够良好匹配真实实验的切向力与法向力。

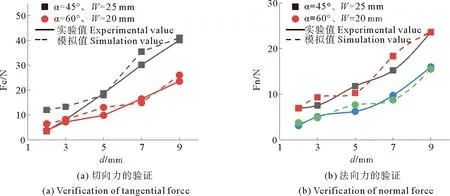
图7 模拟载荷与实验载荷的验证Fig.7 Verification of simulated and experimental loads

4.3 模拟正交实验结果与分析

模拟正交实验结果如表4所示，因为实验指标为切削比能(Specify energy，SPE)只与切向力有关，因此未采集法向力数据。针对SPE分别进行直观分析和方差分析，得出对实验指标影响强弱的相对顺序以及最优组合，最后综合考虑，优化矩形齿几何参数和切削深度。

4.3.1 极差分析 将表4正交模拟实验结果中的SPE进行极差分析，整理数据如表5所示，其中实验综合指标T=3.337 2。从表中可以得出：R1>R2>R3，即前角对切削比能的影响最大，深度其次，刀齿宽度影响最小。本次实验指标代表单位破碎面积上的切向力，表示着破碎的效率，为最小特征值，因此取各因素在不同水平下的最小切削比能所对应的水平。前角取4水平最好，切削深度取2水平最好，刀齿宽度取4水平最好。即最佳参数组合为α=60°、d=5 mm、W=25 mm。

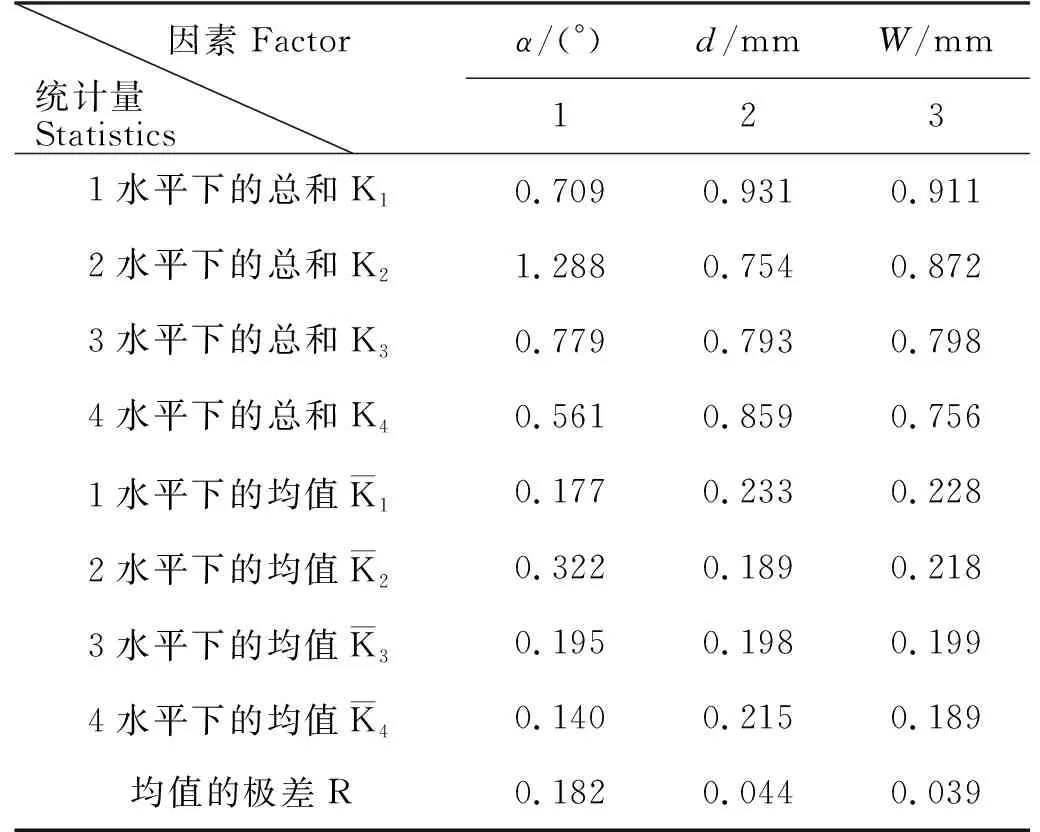
表5 极差分析表Table 5 Range analysis table

4.3.2 方差分析 将表4正交模拟实验结果中的SPE进行方差分析，整理数据如表6所示，查F分布临界值表可得出，前角α有99.5%的概率对于切削比能SPE高度显著，切削深度d和刀齿宽度W对于切削比能SPE基本无影响。结合实际工况和表5所示的极差分析结果，可得出最佳前角α=60°，而切削深度和刀齿宽度对效率基本不影响，故为提高开采量选择最大值，即d=9 mm，W=25 mm。

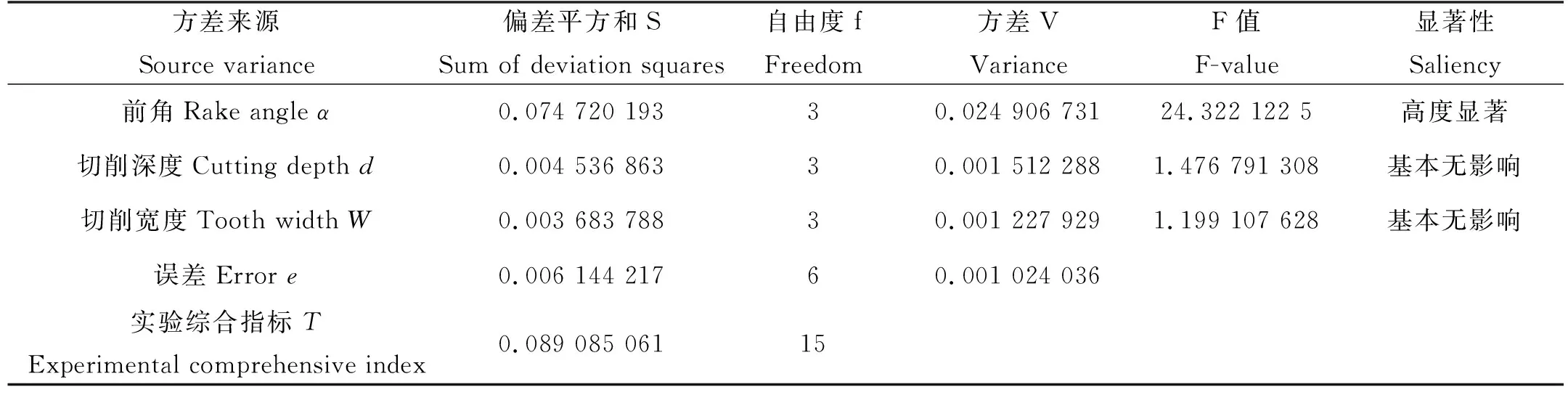
表6 方差分析表Table 6 ANOVA Table

5 结论

(1)对基于相似理论的天然气水合物替代样进行了单齿切削试验，发现切削宽度W、切削深度d均与切削载荷呈正相关，且两者分别在W>15 mm,d>3 mm时，对切削载荷的影响比之前增大。前角α与切削载荷呈负相关，且随前角的增大，对切削载荷影响减小。

(2)基于D-P强度准则建立了三维正交切削的刀齿切向力和法向力解析式。

(3)建立单齿破碎水合物模型，并与试验数据进行对比，发现在切削深度d≥3 mm时，模拟良好，误差在25%内。

(4)基于ABAQUS仿真模型开展正交实验，并进行极差、方差分析，发现前角对切削比能影响显著，而切削深度和刀齿宽度对切削比能基本无影响，得出最优组合为α=60°、d=9 mm、W=25 mm。