对流-扩散方程的hp-局部间断Galerkin有限元方法的最优L∞(H1)误差估计

由同顺

(南开大学数学科学学院,天津300071)

§1 引 言

由于间断Galerkin有限元(DG)方法具有局部守恒性,稳定性,自适应性及高精度等优点,所以近20多年以来,DG方法一直受到人们的广泛重视.DG方法最初由文[1]对于传输方程引入,后来文[2-5]将其拓展到椭圆及抛物问题.文[6]通过引入数值流的方法,把多种DG格式统一起来,给出了DG格式的一致化误差分析.关于DG方法及其综述可参见文献[6-15].

对于对流扩散方程,文[10]提出了局部间断Galerkin有限元(LDG)方法并得到了关于具有常系数线性问题的误差估计.文[16]讨论了非线性对流扩散方程的hp-LDG方法,给出了关于h的最优L2(H1)误差估计以及关于h的次最优L∞(L2)误差估计.文[17]讨论了非线性对流扩散方程的三层隐-显hp-LDG有限元方法,得到了全离散格式的最优L2(H1)误差估计以及次最优L∞(L2)误差估计.据作者所知,关于对流-扩散方程的hp-LDG方法的有关h的最优L∞(H1)误差估计还不多见.本文的目的就是讨论非线性对流扩散方程的hp-LDG方法,使用不同于文[10]的方法,采用文[5-6,12]对于椭圆方程提出的提升算子方法给出了格式的关于h的最优L∞(H1)误差估计.本文的计算结果验证了文中得到的理论结果.关于本文提出的方法应用到其他方程(如：Soblev方程，4阶方程等高阶方程)将在以后讨论.

§2 hp-LDG方法

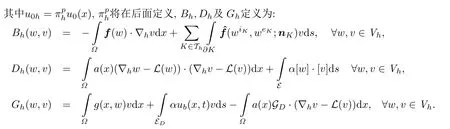
§3 误差估计

§4 数值例子

表 1 ‖u−uh‖L∞(H1)误差阶