基于可接受集的多维风险度量
刘红卫,曾宪福,胡亦均
(1.西藏大学理学院,西藏拉萨850000;2.武汉大学数学与统计学院,湖北武汉430072)
§1 引 言
经典的风险度量VaR由于不满足分散投资能减少风险这一市场基本要求,因此文[1]利用公理化的方法提出了一致风险度量的概念,奠定了公理化方法研究风险度量的基础.在文[1]中提出了与一致风险度量相对应的满足四条公理的可接受集概念,并通过两个定义实现了可接受集和一致风险度量之间的等价刻画.事实上货币具有流动性特征,一致风险度量中的正齐次性在实际金融市场中并不能得到满足.文[2-4]分别独立的推广了一致风险度量,在弱化一致风险度量公理化体系中正齐次性和次可加性的基础上,提出了凸风险度量.
以上文献都是基于一维情况的讨论.近年来,关于多维头寸的风险度量已成为研究的热点.文[5-6]建立了基于数量值角度的多维凸风险度量研究框架,并给出了相应表示定理,并在文中提出了满足四条公理的可接受集概念,将多维数量值的凸风险度量和可接受集联系到了一起.文[7-8]推广了文[5]的结论,在更为一般空间上给出了基于数量值角度的多维现金次可加和现金可加风险度量表示定理.以上文献的结论主要是从风险度量的公理化角度对风险进行研究,并给出相应表示定理.文[9-10]改变了传统公理化研究风险的方法,从可接受集角度出发,提出了单个金融头寸简单准备金和广义准备金的概念,并给出了相应的风险表示定理.
本文将文[9]的结论进行了推广,在一般空间上建立了基于可接受集的多维风险度量研究框架,从准备金和风险对冲角度提出了两个风险度量的概念,进一步给出可接受集,对冲策略,价格函数在满足一定条件下相应的表示定理.
§2 准备知识
设d≥1是一个固定的正整数,对于1≤i≤d,设(Ω,Fi)是一固定的可测空间,(Ω,Fi,P)是一固定的概率空间.用Gi记L∞(Ω,Fi)空间,用Hi记Lp(Ω,Fi,P)空间,1≤p≤∞,1≤i≤d.XdX1×···×Xd,1≤i≤d,Xi为Gi或Hi.当X=(X1,···,Xd)∈Xd时,定义

若Xi是Gi,则定义为,若Xi是Hi,则定义为,则是一个Banach 空间.记

其中当Xi是Gi时,M1,f(Xi)表示M1,f(Ω,Fi),其中M1,f(Ω,Fi)表示在空间(Ω,Fi)上有限可加测度的全体,且在全空间Ω上测度取值为1.当Xi是Hi时,M1,f(Xi)表示M1,f(Ω,Fi,P),其中M1,f(Ω,Fi,P)表示在空间(Ω,Fi,P)上关于P绝对连续的有限可加测度全体,且在全空间Ω上测度取值为1,具体的有
(1)若pi=+∞,则M1,f(Xi)表示M1,f(Ω,Fi,P).
(2)若pi=1,则M1,f(Xi)表示集合{Qi|Qi∈M1,f(Ω,Fi,P),
(3)若1 ∀X=(X1,···,Xd),Y=(Y1,···,Yd),若X≤Y意味着Xi≤Yi,1≤i≤d,X+Y=(X1+Y1,···,Xd+Yd).设0=(0,···,0),1=(1,···,1),ei=(0,···,1,···,0)为单位向量,其中元素1位于第i个位置,下文中使用的ei均指i为任意固定的值. 引理2.1(Fenchel-Moreau定理)[9]设(E,τ)是一个局部凸拓扑向量空间,E∗是E的拓扑对偶空间.f:E→R∪{∞}是一个下半连续的凸函数,且f是适当的(f∞),则f的双共轭f∗∗就是其自身,且有 定义2.1[6]称映射ρ:Xd→R是币值风险度量,若ρ满足如下性质 (1)单调性:对任意满足X≤Y的X,Y∈Xd,有ρ(X)≥ρ(Y). (2)现金可加性:对任意的X∈Xd,m∈R,有ρ(X+mei)=ρ(X)−m,1≤i≤d. 从金融意义上讲,币值风险度量的现金可加性表示在d维头寸X某个位置i上追加m单位的资金1≤i≤d,均可使得头寸X的风险减少m单位的资金. 定义2.2[6]设ρ是币值风险度量且满足凸性,即对任意的λ∈[0,1]和X,Y∈Xd,有 ρ(λX+(1−λ)Y)≤λρ(X)+(1−λ)ρ(Y), 则称ρ为多维凸风险度量.若多维凸风险度量ρ满足正齐次性,即对任意的λ≥0,有ρ(λX)=λρ(X),此时称ρ为多维一致风险度量. 定义2.3[6]称A⊂Xd为可接受集,若满足如下性质 (1)A是闭的. (2)单调性:X,Y∈Xd,若X≥Y,Y∈A,则X∈A. (3)X+mei∈A⇔X+mej∈A,i,j=1,···,d. (4)RdA. 在本文中,对任意的X∈Xd和,使用如下约定符号 定义3.1设A为一个可接受集,定义映射ρA:Xd→R为 称映射ρA是由A诱导出的多维简单风险度量. 从定义3.1来看,简单风险度量的金融含义就是要使风险头寸X变的可以接受时,在d维X的某个分量i上所需要追加的最少资金量.从准备金角度来看ρA(X)就表示头寸X的准备金. 当多维头寸X=(X1,···,Xd)退化到一维情况时,式(3.1)的形式与[1,3]给出ρA的形式是一致的. 性质3.1设A是可接受集,则多维简单风险度量ρA有如下性质: (1)ρA是币值风险度量. (2)若A是凸集,则ρA是多维凸风险度量. (3)若A是凸锥,则ρA是多维一致风险度量. 证(1)现金可加性:对任意的X∈Xd,a,m,b∈R,有 单调性:对任意满足X≤Y的X,Y∈Xd,1≤i≤d,有 {m1∈R|X+m1ei∈A}⊆{m2∈R|Y+m2ei∈A}, 因此就有 inf{m1∈R|X+m1ei∈A}≥inf{m2∈R|Y+m2ei∈A}. 即ρA(X)≥ρA(Y).故ρA是币值风险度量. (2)由(1)知ρA是币值风险度量,下证ρA满足凸性. 对任意的X,Y∈Xd,m,n∈R,1≤i≤d,使得X+mei∈A,Y+nei∈A.对任意的λ∈[0,1],由A的凸性可知 λ(X+mei)+(1−λ)(Y+nei)∈A. 由于ρA满足现金可加性,于是就有 即ρA(λX+(1−λ)Y)≤λρ(X)+(1−λ)ρ(Y),因此ρA是多维凸风险度量. (3)A是凸集,由(2)知ρ是多维凸风险度量. 又因为A是锥,对于任意的λ≥0,有λX∈A,于是就有 由定义2.2可知,ρA是多维一致风险度量.命题得证. 设ρ是币值风险度量,则可由ρ诱导出一个可接受集 对于可接受集Aρ,由定义3.1可得 本小节下文在不引起混淆的情况下,用A来表示Aρ.由于ρ是币值风险度量,满足单调性和现金可加性,于是显然有如下性质成立. 性质3.2设A满足(3.2)式,则有 (1)A满足单调性. (2)若ρ满足凸性,则A是凸集. (3)若ρ满足正齐次性,则A是正极锥. 性质3.3设ρA是定义在Xd上的币值风险度量,则ρA关于范数是Lipschitz连续的. 证对任意的X,Y∈Xd,有 定理3.1设ρA是下半连续的多维简单风险度量.如果可接受集A是凸的,则ρA是多维凸风险度量,且ρA可以表示为如下形式 证由性质3.1(1)和(2)可知,ρA满足单调性,现金可加性和凸性.由定义2.2知多维简单风险度量ρA是多维凸风险度量.ρA是下半连续的,由引理2.1可得 定义3.2设A是可接受集,对任意的X,Y∈Xd和C⊂Xd,价格函数v:C→R,定义映射ρ(A,C,v):Xd→R为 称映射ρ(A,C,v)为由A诱导的多维广义风险度量. 对任意的m∈R,若Y=mei∈C,v(mei)=m,则广义准备金就退化到了如下形式 式(3.5)与[6]所定义的ρA是一致的. 式(3.4)的各个符号有如下的金融解释,可接受集A是符合监管机构或投资机构风险管理要求的集合,C为可交易的风险资产或是能采取的对冲策略集合,v是风险资产的价格或是采取某一对冲策略时的费用,称为价格函数.ρ(A,C,v)表示采用策略或交易风险资产Y来对冲X风险头寸时的最小费用. 性质3.4设映射ρ(A,C,v):Xd→R是多维广义风险度量,则有 (1)若v是凸映射,并且A和C是凸集,则ρ(A,C,v)是凸映射. (2)若A是单调的,则ρ(A,C,v)是单调的,即对任意的满足X≥Y的X,Y∈Xd,有 ρ(A,C,v)(X)≤ρ(A,C,v)(Y). (3)若A和C是正极锥,且v是正齐次的映射,即对任意的λ>0,X∈Xd,有v(λx)=λv(X).则ρ(A,C,v)是正齐次的映射. 证(1)对任意的X1,X2∈Xd,λ∈[0,1],Y1,Y2∈C,使得X1+Y1,X2+Y2∈A, 有A和C的凸性可得 Y=λY1+(1−λ)Y2,Y+λX1+(1−λ)X2∈A 由于v是凸的,则有 所以ρ(A,C,v)是凸映射. (2)对任意的X1,X2∈Xd,Y∈C,且X1≥X2,则有X1+Y≥X2+Y.由A的单调性可知,{Y|X1+Y∈A}⊇{Y|X2+Y∈A},因此 (3)对任意的Z∈A,Y∈C,λ≥0,由于A和C是正极锥,则λZ∈A,λY∈C,因此 多维广义风险度量ρ(A,C,v)与因素A,C,v有关,性质3.4(1)表明,在v是凸映射,且A和C是凸集时,ρ(A,C,v)仅是一凸映射,这与性质3.1(2)是不同的,原因在于现金可加性未必成立.以下给出多维广义风险度量ρ(A,C,v)现金可加的定义. 定义3.3设C⊂Xd,Z∈C,v:C→R,称多维广义风险度量ρA,C,v:Xd→R关于(C,v)是现金可加的,若满足 对任意的Z=(Z1,···,Zd)∈C,如果则式(3.6)变为ρ(A,C,v)(X+Z)=这与文献[7]中投资组合凸风险度量的平移不变性质是等价的.如果Ymei∈C,m∈R时,式(3.6)变为ρ(A,C,v)(X+mei)=ρ(A,C,v)(X)−m,这与Rüchendorf多维风险度量定义中的现金可加性是等价的.当多维向量X=(X1,···,Xd)退化成一维情况时,式(3.6)变为ρ(A,C,v)(X+m)=ρ(A,C,v)(X)−m,这与文献[1,3]中的平移不变性是一致的.式(3.6)表明,如果在多维头寸X上交易资产Z,可以使得风险头寸X的风险恰好减少Z的价格v(Z). 性质3.5设线性子空间C⊂Xd,v是C上的线性映射,则广义风险度量ρ(A,C,v)满足现金可加性. 证对任意的X∈Xd,若Z∈C,Y∈C,则Y−Z∈C. 性质3.6设ρ(A,C,v)是定义在Xd上的多维广义风险度量,满足现金可加性,且价格函数v关于范数k·k是Lipschitz连续,则ρ(A,C,v)关于范数是Lipschitz连续的. 证对任意的X,Y∈Xd,有 下面讨论集合Aρ(A,C,v)在一定条件为可接受集. 性质3.7设Aρ(A,C,v)满足(3.7)式,则有 (1)若ρ(A,C,v)满足单调性,则Aρ(A,C,v)满足单调性. (2) 若ρ(A,C,v)满足凸性,则Aρ(A,C,v)是凸集. (3)若ρ(A,C,v)满足正齐次性,则Aρ(A,C,v)是正极锥. 证(1)对所有满足X≤Y,且X∈Aρ(A,C,v),由ρ(A,C,v)的单调性知 故有Y∈Aρ(A,C,v),因此Aρ(A,C,v)满足单调性. (2)对所有的X,Y∈Aρ(A,C,v)和任意的λ∈[0,1],由ρ(A,C,v)的凸性可知 ρ(A,C,v)(λX+(1− λ)Y)≤λρ(A,C,v)(X)+(1−λ)ρ(A,C,v)(Y)≤0. 故有λX+(1−λ)Y∈Aρ(A,C,v),因此Aρ(A,C,v)是凸集. (3)对所有的X∈Aρ(A,C,v)和任意的λ≥0有 ρ(A,C,v)(λX)=λρ(A,C,v)(X)≤0, 故有λX∈Aρ(A,C,v),因此Aρ(A,C,v)是正极锥. 当ρ(A,C,v)满足单调性,正则性,且价格函数v是Lipschitz连续时,满足(3.7)式的Aρ(A,C,v)是可接受集.在不引起混淆的情况下,本小节下文使用Aρ来替代满足(3.7)式的可接受集Aρ(A,C,v). 对于可接受集Aρ,根据定义3.2可知,多维广义风险度量ρAρ,C,v可以记为如下形式 由(3.7)式和(3.8)式易知ρ(Aρ,C,v)=ρ(A,C,v). 定理3.2设ρ(A,C,v)是定义在Xd上下半连续的广义准风险度量.可接受集Aρ(A,C,v)是单调的,凸的,C⊂Xd是一个凸的线性空间,v:C→R是一凸线性映射,则ρ(A,C,v)为多维凸风险度量,且有如下的表示形式 证 根据性质3.4和3.5可知,ρ(A,C,v)满足单调性,凸性现和金可加性.ρ(A,C,v)满足正则性. 定理3.2表明,ρAC,v的惩罚函数可以分解为一个关于可接受集Aρ的惩罚函数,一个关于对冲策略集C和价格v的惩罚函数.当C∈R,且v是恒等映射时,αC,v(Q)=0.此时,惩罚函数,这就退化到定理3.1的表示形式. 实例1考虑一个多维现金可加风险度量ρA:Xd→R,其可接受集定义为 实例2考虑一个多维的效用函数,设其中γ>0,定义下面的可接受集: 实例3考虑一个二维的效用函数,令 本文改变了传统公理化研究风险度量的方法,从可接受集角度出发,建立了一般空间上两种多维风险度量的研究框架,并利用Fenchel-Moreau定理等给出了相应的表示定理,推广了Frittelli M和Scandolo G(2006)的结论.
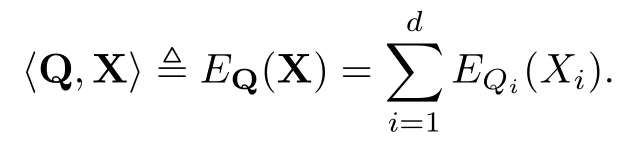
§3 主要结论
3.1 多维简单风险度量





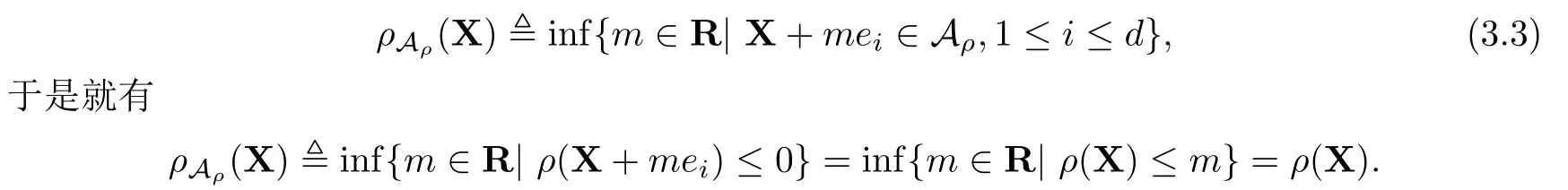


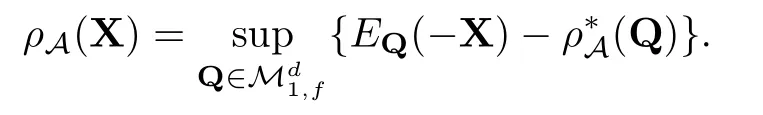
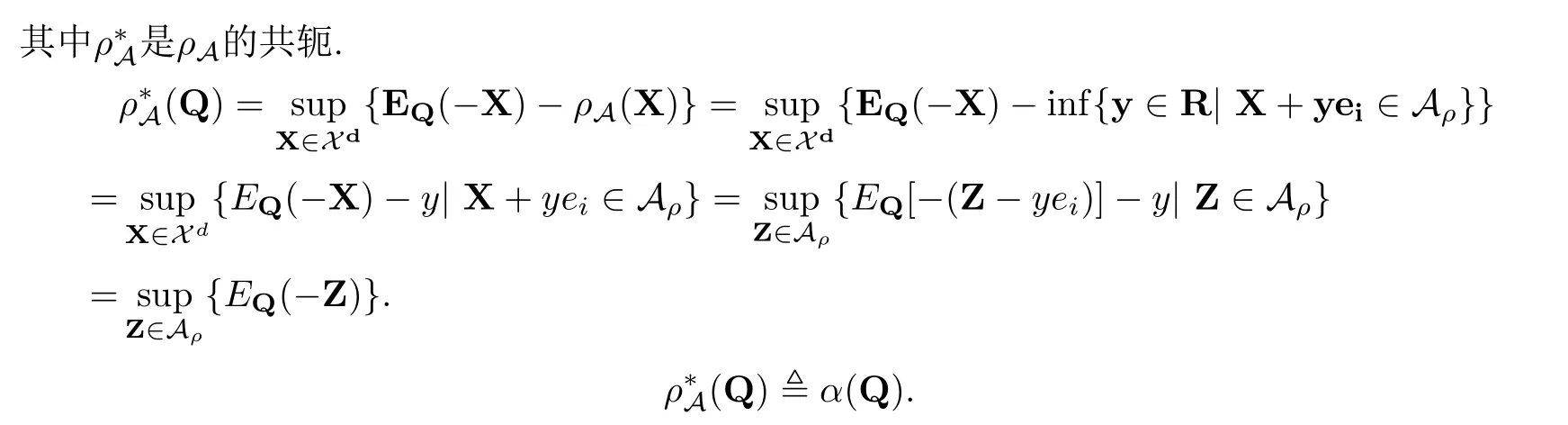
3.2 多维广义风险度量


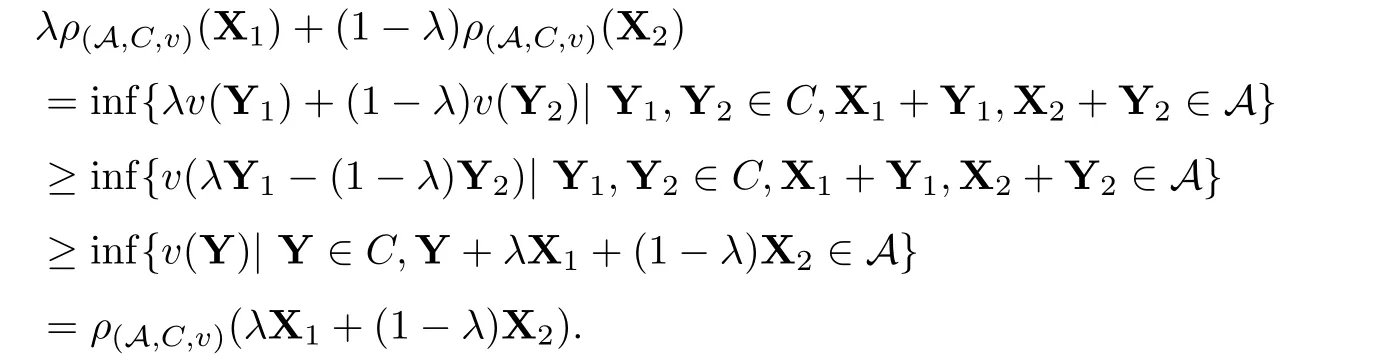



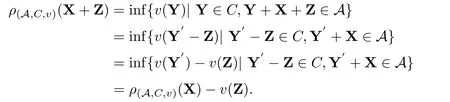

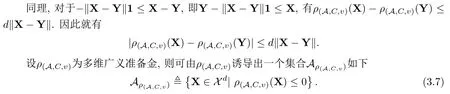







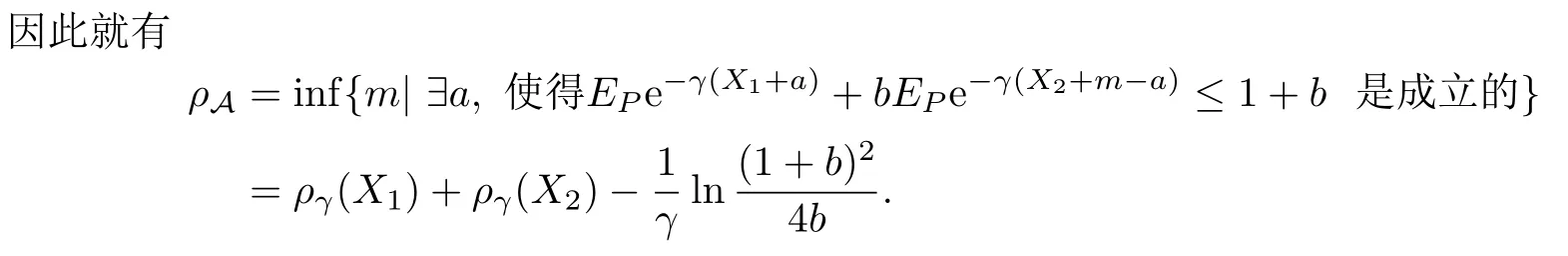
§4 小结

