一类时间相依复合更新风险模型损失过程的尾概率渐近估计
唐风琴,丁文文
(淮北师范大学数学科学学院,安徽淮北235000)
§1 引 言
文献[1]介绍了一类复合更新风险模型,具体如下:

在假设A-C下,文献[1]假设索赔额服从宽正则尾分布,得到了模型(1)的精细大偏差.在文献[1]的基础上,文献[2]考虑了一致变化尾分布下模型(1)的精细大偏差.模型中变量之间独立性假设仅仅为了计算的简便,是不符合实际需要的.文献[3]假设模型(1)中的索赔次数之间存在相依结构并考虑了该模型的精细大偏差.文献[4]考虑了具有相依索赔额的复合更新风险模型,假设事故发生时间间隔之间也是不独立的,得到了该模型的精细大偏差.文献[5]在Zn=1,n≥1情形下得到了时间相依风险模型的大偏差,所谓时间相依即索赔到达时刻与索赔额之间具有相依结构.在此基础上,本文在模型(1)中考虑了单次事故引起的索赔次数与索赔时间间隔之间具有相依结构,讨论模型(1)的精细大偏差及有限时破产概率的渐近估计.除了假设A-C,还需要以下假设:

§2 预备知识
首先介绍重尾分布.设X为一非负随机变量,分布函数为F(x).

文献[8]介绍了一类相依结构.
定义2.1随机变量Y1,Y2,...称为宽上象限相依(WUOD),若对任意的m≥1,x1,x2...,存在非负实函数{gU(m);m≥1}成立

注2.1对任意的m≥1,若gU(m)=M>0,则称Y1,Y2,...为广义负上限相依(extended negative upper orthant dependent(ENUOD)).若M=1,则称Y1,Y2,...为负上限相依(negative upper orthant dependent(NUOD)).详见参考文献[9–11].
下面给出本文的主要结论,其中定理2.2给出了模型(1)的大偏差结果,定理2.3给出了模型(1)有限时破产概率的渐近估计.
定理2.1在假设B-D下,考虑随机和.假设对任意的0<α<1,成立

那么对任意的γ>0,当x≥γm,m→∞时一致成立
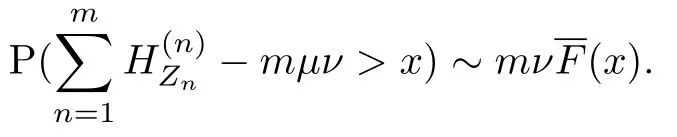
条件(3)详见文献[12].
定理2.2在假设A-E和条件(3)下考虑复合更新模型(1).∀γ>0,当x≥γλ(t),t→∞时一致成立

定理2.3在假设A-E和条件(3)下考虑复合更新模型(1).当0 首先给出证明中需要用到的引理.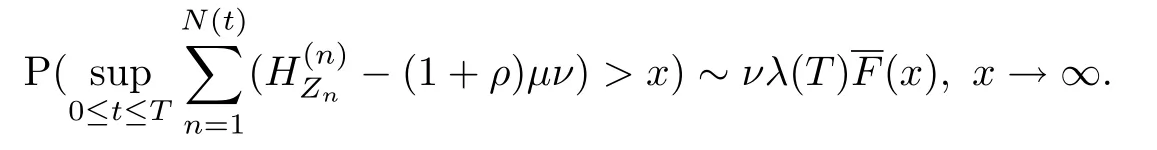
§3 主要结论的证明







