四元Heisenberg群上的Twistor-变换与Penrose-积分公式

任光震

(浙江大学数学科学学院,浙江杭州310027)

§1 引 言

自上世纪下半叶以来,Twistor理论取得了丰富的成果和长足的进展.Twistor理论是由Penrose在研究四维时空中的场方程引入的.具体地,首先给出闵科夫斯基空间与三维复射影空间CP3的一种对应,该对应即为著名的Twistor变换,借助该变换可以将闵科夫斯基空间上的很多场方程的解表示为CP3中某类开子集上的齐次全纯函数的轨道积分,该积分就是著名的Penrose-积分公式.Penrose积分公式具有广泛的应用,例如在某些复空间或四元数空间上,相应的Penrose型积分公式即为Cauchy-Fueter方程的解(见[1]-[8]).Baston和Eastwood用复几何和表示论将Twistor变换推广到一般的G/P空间上,其中G为半单李群,P为其抛物子群(见[9]).本文从表示论的角度研究四元Heisenberg群上的Twistor理论.并考虑四元Heisenberg群上的切向k-Cauchy-Fueter方程(见[10]-[13]),给出其解即为四元Heisenberg群上的Penrose型积分公式.

§2介绍了李代数sp(2n+4,C)中的抛物子代数.利用[14]的方法给出了李群Sp(2n+4,C)关于各抛物子群陪集的坐标卡.§3通过介绍各抛物子代数及相关Dynkin-图的双纤维化,给出各抛物子群陪集的双纤维化,进而得到四元Heisenberg群上的Twistor变换.§4给出了四元Heisenberg群上的Penrose型积分公式,证明了该积分公式可以给出很多非平凡的k-CF函数.

§2 预备知识

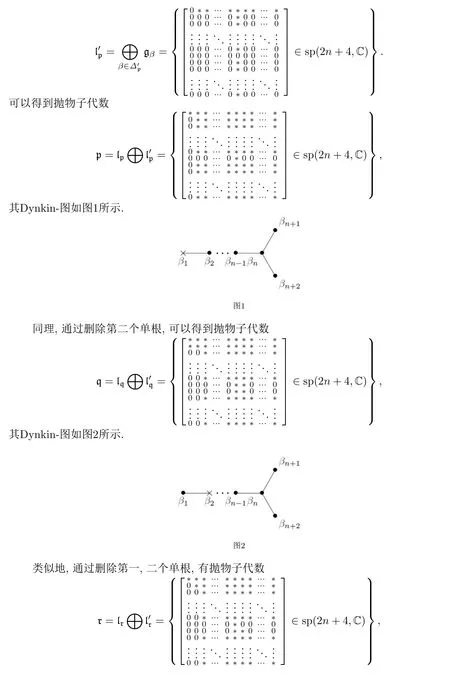
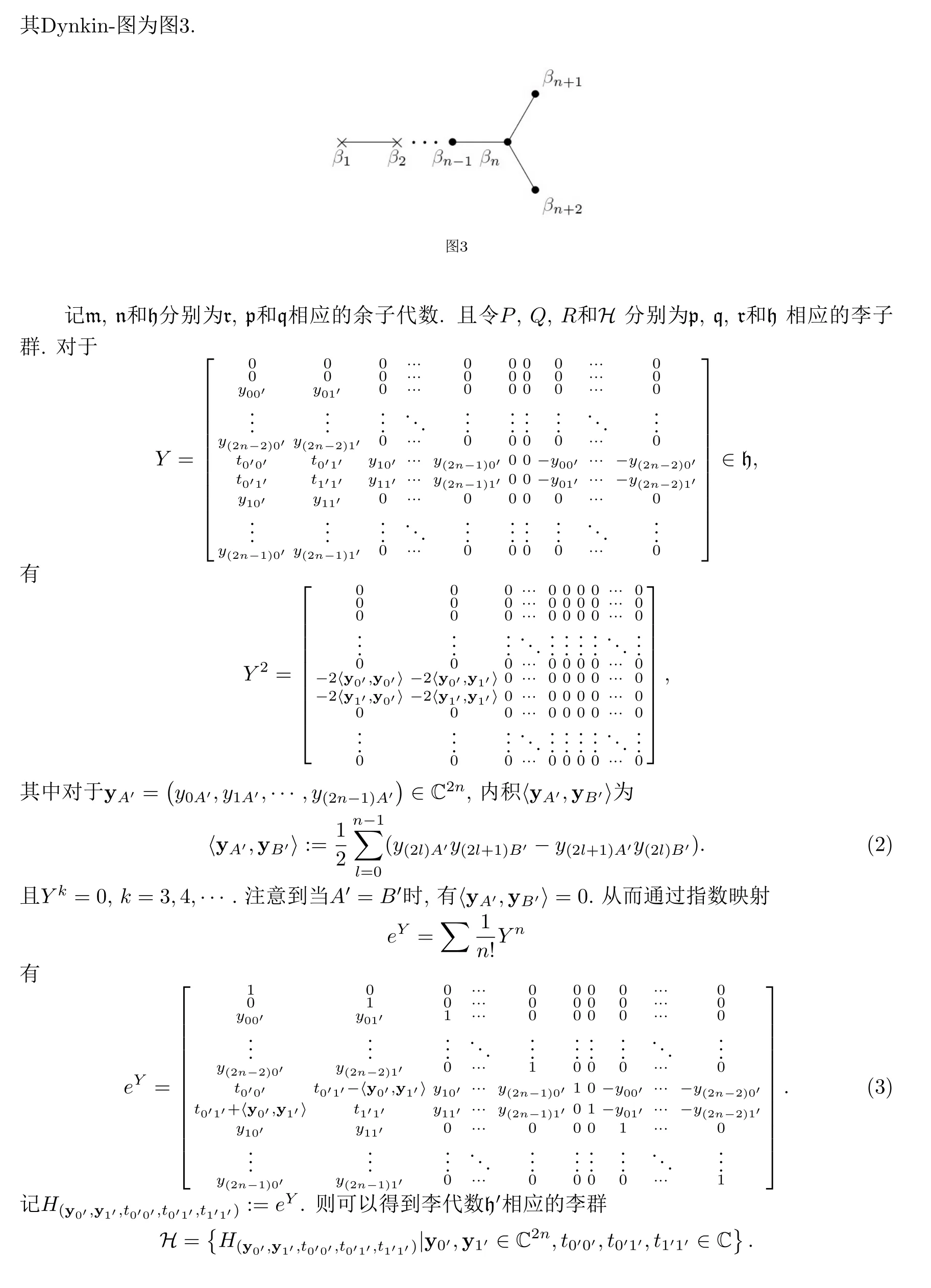
§3 Twistor-变换

本节将借助sp(2n+4,C)中抛物子代数的的双纤维化(如图4所示),

图4

§4 Penrose-积分公式和四元k-CF多项式