基于局部均值分解和迭代随机森林的脑电分类
秦喜文,郭 宇,董小刚,郭佳静,袁 迪
(长春工业大学 a.数学与统计学院;b.研究生院,长春 130012)
0 引 言
癫痫是短暂和意外的脑电紊乱,是一种因脑部损伤而严重影响人类健康的脑部疾病。癫痫发作的迹象不仅可在癫痫患者的大脑中找到,也可在正常人的大脑中找到[1]。脑电信号是非线性、非平稳的时序信号,可通过头皮或颅内电极上的传感器检测,这些信号是神经元膜电位非常丰富的外部表现[2]。准确评估、术前评估、癫痫预防以及紧急警报都依赖于癫痫发作的快速检测。医生可通过监测脑电信号评估大脑的状态。因此,脑电信号在癫痫发作的检测和鉴别中起着重要作用。传统的癫痫检测方法是神经学专家对长期脑电图记录的目视扫描。然而,这是一项耗时的任务,并且由于大量的脑电图数据和不同神经学专家的临床判断标准不同,诊断可能不准确[3]。因此,开发智能型癫痫自动检测系统显得尤为迫切,具有重要的实际意义。
1875年,英国医生Caton[4]发现动物大脑存在电活动现象。 1934年,经Adrian等[5]证实,人类的脑电信号获得了世界各界的认同。在此之后,众多学者开始对脑电图进行相关研究,并把这部分知识应用于药理学、生物学和医学等诸多领域。Das等[6]从经验模态分解和离散小波变换两方面对局灶性和非局灶性脑电图进行了综合分析。Li等[7]提出了一种基于经验模态分解和支持向量机的癫痫发作期脑电特征提取和模式识别方法。还有一些学者将时频分析与机器学习相结合识别诊断脑电信号,Zhuang等[8]给出了一种基于经验模态分解(EMD:Empirical Mode Decomposition)的特征提取和脑电信号识别方法;Chen等[9]提出了一种利用经验模态分解和近似熵的脑电特征提取方法,设计了一种将深度信念网络与支持向量机相结合的分类方法,提取特征向量,识别出人类快乐、平静、悲伤和恐惧4种主要情绪;陆苗等[10]利用改进的经验模态分解处理脑电信号,用所得固有模态函数(IMF:Intrinsic Mode Function)求取能量熵等特征值提高分类精度;韩敏等[11]针对单一极限学习机在癫痫脑电信号研究中分类结果不稳定、泛化能力差的缺陷,提出一种基于互信息的AdaBoost极限学习机分类算法。随着计算机科学技术的不断发展,脑电信号的分析方法层出不穷,越来越多样化,陆续出现了非线性分析法[12]、时频分析法[13-14]、高阶谱分析法[15]等系列现代化分析方法[16]。笔者针对非平稳、非线性的脑电信号,提出一种基于局部均值分解和迭代随机森林相结合的脑电信号分类方法。利用局部均值分解,将脑电信号分解成若干个乘积函数分量和一个残余分量,然后对分解后的所有分量进行特征提取,最后使用随机森林和迭代随机森林等方法进行分类。
1 算法描述
1.1 局部均值分解
局部均值分解(LMD:Local Mean Decomposition)方法可逐步地将调频信号与调幅包络信号分离。通过平滑处理原始信号,将平滑后的信号从原始信号中减去,然后对包络函数进行估计,对结果进行幅度解调实现分离。通过使用由原始信号的连续极值之间的时间延迟加权的移动平均可获得包络估计和原始信号的平滑版本。如果得到的信号不具有平坦包络,则重复该过程,直到获得具有平坦包络的调频信号。然后,从调频信号中计算瞬时频率,将所有包络估计函数相乘得最终包络,将该包络乘以频率调制信号以形成乘积函数,从原始信号中减去该乘积函数,对得到的信号重复整个过程,以产生具有相关包络和瞬时频率的第2乘积函数。继续该分解,直到剩余信号不再包含振荡,得到一个单调函数为止。
LMD算法步骤如下[17]。
1)从原信号中记录全部局部极值点ni,对信号中相邻的2个局部极值点取均值
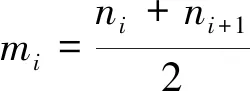
(1)
将所有局部均值mi用直线串联起来,然后利用滑动平均法对局部均值线段进行平滑处理,得局部均值函数m11(t)。
2)利用局部均值点,求出俩相邻极值点之间的包络估计值
ai=|ni-ni+1|/2
(2)
将全部相邻2个包络估计值ai用直线连接,然后采用滑动平均方法进行平滑处理,得包络估计函数a11(t)。
3)将局部均值函数m11(t)从原信号x(t)中剔除,得
h11(t)=x(t)-m11(t)
(3)
4)对h11(t)进行解调,用h11(t)除以包络估计函数a11(t),得
s11(t)=h11(t)/a11(t)
(4)
计算s11(t)的包络估计函数a12(t),若a12(t)≠1,说明s11(t)并不是一个纯调频信号,将重复上述解调过程,直到使s1n(t)成为一个纯调频信号为止,即-1≤S1n(t)≤1,且其包络函数a1(n+1)(t)=1,有

(5)
其中

(6)
迭代终止条件为

(7)
a1n(t)≈1
(8)
5)在上述迭代过程中,将求得的所有包络估计函数相乘,得包络信号
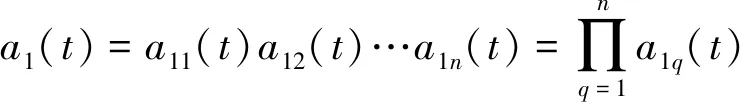
(9)
6)用包络信号a1(t)和纯调频信号s1n(t)相乘,可得原信号的乘积函数(PF:Product Function)
P1(t)=a1(t)s1n(t)
(10)
7)将一个分量P1(t)从原信号x(t)中剔除,获得一个全新的信号u1(t),再将u1(t)作为原始数据重复上述步骤,循环k次,直到uk为一个单调函数为止

(11)
所有的乘积函数分量和uk重组,可求出原始信号

(12)
这说明LMD分解没有造成原信号的丢失。
1.2 特征提取
对局部均值分解后得到的各阶乘积函数提取重要特征,其中包括均值、标准差等一系列简单统计量,以及能量熵和信息熵。
1.2.1 变异系数
变异系数(CV:Coefficient of Variation)是衡量资料中各观测值变异程度的统计量,为标准差与平均数的比值
C=σ/μ
(13)
其中
其中l为数据长度,即分解后的乘积函数长度。
1.2.2 波动指数
波动指数是描述信号波动幅度大小的一个统计量,在实验中可见癫痫发作间期信号的波动剧烈程度小于发作期,且相对稳定。其定义为

(14)
1.2.3 能量熵
在不同状态下,脑电振动信号的频率分布会发生变化,故癫痫发作期与发作间期脑电信号的能量也会发生变化。一般情况下,发作间期脑电信号中的能量分布是均匀的、不确定的,因而大于癫痫发作期脑电信号。因此可用LMD能量熵判断患者是否处于癫痫状态。
乘积函数分量的能量熵通过以下步骤计算[18]。首先,计算第i个PF的能量
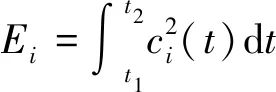
(15)
其中t1和t2分别为信号开始和结束时间。之后计算整个PF的能量
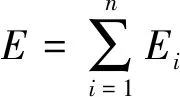
(16)
最后,定义整个PF的能量熵为

(17)
1.2.4 信息熵
信息熵是一个数学的抽象概念,是为了消除数据不确定性的度量。癫痫发作期信号的信息熵通常比发作间期的信息熵低。其定义为
H(x)=E[I(x)]=E[log2(1/p(xi))]=-∑p(xi)log2(p(xi)),i=1,…,n
(18)
其中x表示随机变量,与之相对应的是所有可能输出的集合,定义为符号集;p(x)表示输出概率函数。变量的不确定性越大,熵也就越大。
利用LMD分解波恩癫痫研究中心数据库中癫痫发作间期与发作期数据,计算分解后乘积函数的特征值。
1.3 迭代随机森林
迭代随机森林(iRF:iterative Random Forest)在随机森林的基础上通过对选定的特征进行迭代重新赋权(iterative re-weighting),得到一个带有特征权重的随机森林,然后将泛化的随机交叉树作用于带有特征权重的随机森林上,识别特征的高阶交互作用,保证其具有较高的预测能力。迭代随机森林的具体工作流程如下[18]。
1)对随机森林进行迭代重新赋权,给定迭代次数K,在数据集D上,通过迭代生成K个具有特征权重的随机森林,记为RF(ωk),k=1,…,K。初始权重k=1时,ω=(1/p,…,1/p),并计算p个特征的重要性,即基尼纯度的平均减少,记为υ(1)=(υ1,…,υp)。令ω(k)=υ(k-1),即用随机森林特征的重要性作为其权重。
2)将泛化的随机交叉树作用于RF(ωK),产生一组交叉作用集S。
3)计算Bagged稳定得分,使用“外层”(out layer)自助法,以评价重现交叉作用的稳定性。生成自助抽样数据集D(b),b=1,…,B,在D(b)上拟合随机森林RF(ωK),并且使用泛化随机交叉树识别交互作用集S(b),给出交叉作用集S的稳定分数公式

(19)
2 实验结果
2.1 脑电信号分解
实验数据取自德国波恩大学癫痫研究中心数据库。该数据库是目前癫痫脑电信号研究最为普遍采用的脑电数据库,其中包含5个子集,分别标号为A、B、C、D、E。每个子集包含100个实验样本,每个样本采样时间为23.6 s、频率为173.61 Hz,每个样本信号包含4 097个样本点。笔者选取数据库中数据集D和数据集E,分为癫痫发作间期和发作期进行分析。图1给出了发作间期与发作期的原始癫痫脑电信号。

a 癫痫发作间期 b 癫痫发作期
图1a为一组癫痫发作间期的脑电信号样本,可见其信号波动程度较大,但具有一定的规律性。图1b为一组癫痫发作期的脑电信号样本,可见该信号波幅较小,且不稳定。由图1可知,两种脑电信号在波动幅度和稳定性方面具有明显差异。
图2和图3给出了LMD分解后癫痫发作期和发作间期的脑电信号PF分量。癫痫发作间期脑电信号经LMD分解后得到4个乘积函数和1个残余分量(见图2);癫痫发作期脑电信号经LMD分解后得到4个乘积函数和1个残余分量(见图3)。
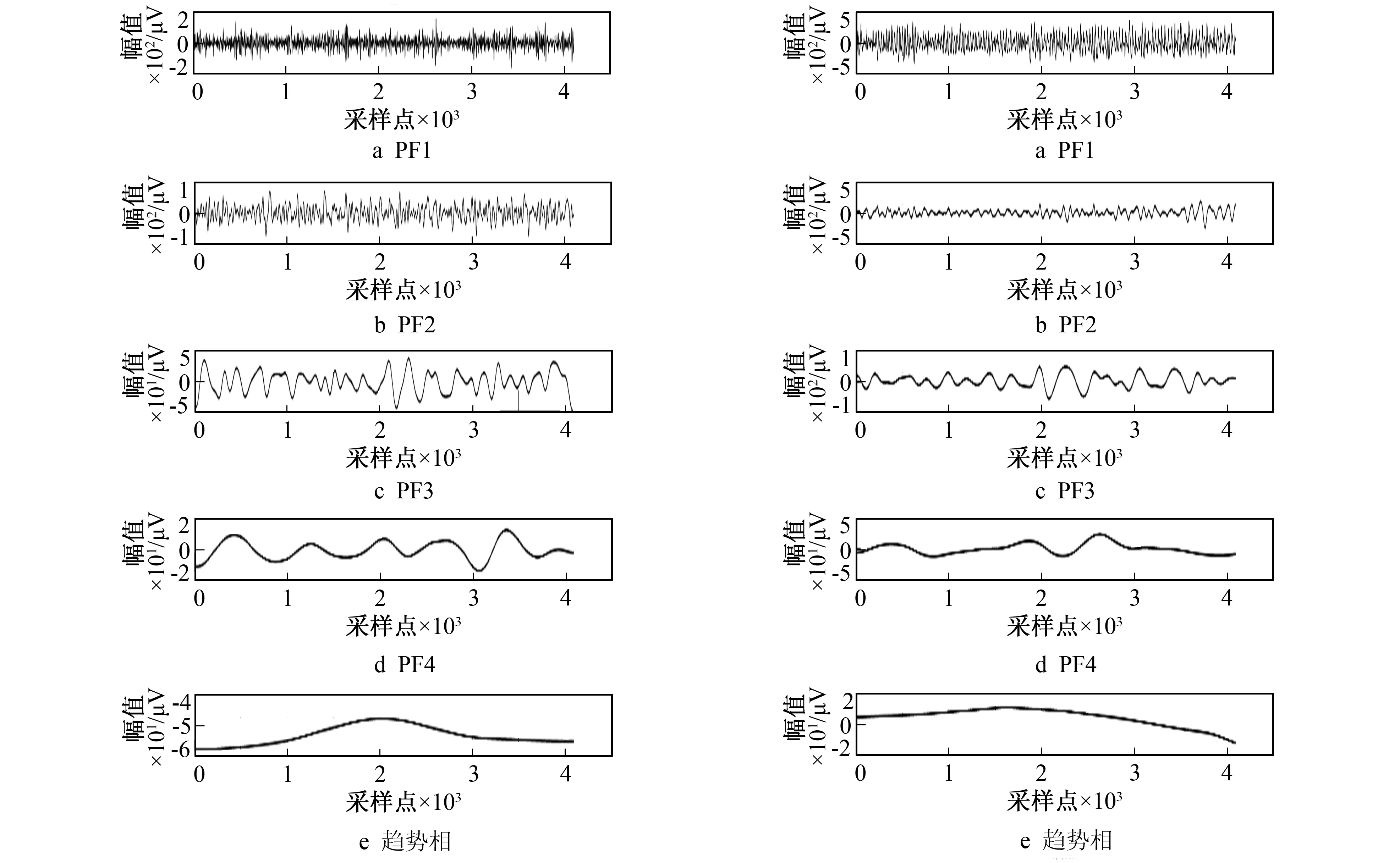
图2 发作间期EEG分解后的PF分量 图3 发作期EEG分解后的PF分量Fig.2 PF of EEG after decomposition in interictal period Fig.3 PF of EEG after decomposition in ictal period
2.2 脑电信号特征提取
对癫痫脑电信号发作间期和发作期的200个样本信号,经过局部均值分解后提取所有乘积函数的特征向量。表1为癫痫脑电信号发作间期的特征样本,表2为癫痫脑电信号发作期的特征样本。

表1 癫痫脑电信号发作间期特征样本

表2 癫痫脑电信号发作期特征样本
2.3 癫痫脑电信号分类结果
笔者分别选取支持向量机、随机森林及迭代随机森林3种机器学习方法对局部均值分解后所求特征向量进行分类,并比较分类结果(见表3)。实验样本共1 284个,选取900个作为训练集,另外384个作为测试集,结果表明,LMD与迭代随机森林相结合的算法对癫痫发作间期和发作期EEG的乘积函数分类效果最佳,正确识别率为98.177%。

表3 癫痫脑电信号分类结果比较
3 讨 论
在临床医学上,癫痫脑电信号的自动检测和分类有着重要意义。Zhang等[19]提出了一种基于LMD和SVM结合的脑电信号分类方法,证明了在诊断脑电信号方面,脑电信号自适应分解与机器学习相结合的全新算法具有可行性和有效性。
在处理非平稳和非线性信号时,LMD相对于其他时频分析方法具有很多优势。LMD采用平滑处理的方法形成局部均值函数和局部包络函数,这既保持了EMD分解的优势,又可避免像EMD分解中采用3次样条函数形成上下包络时产生的过包络、欠包络现象,此外LMD端点效应的扩散程度远小于EMD。此方法除了分解脑电信号,还可应用于其他领域,如机械故障、金融股市和环境质量等。在目前众多分类算法中,iRF不仅具有和RF一样的抗噪音和抗干扰能力,且经过多次迭代赋权,可充分利用每棵树的分类能力,使整体分类效果得到提升。
通过对德国波恩大学癫痫研究中心的脑电数据进行实验分析,将局部均值分解方法的自适应分解特性与迭代随机森林的多次赋权相结合,使LMD-iRF算法分类结果的准确率高于LMD-SVM和LMD-RF算法。此方法不仅可用于生物医学信号分析处理,还可应用在环境监测、机械故障诊断和金融分析等领域,是一种具有较高精度的分类算法。
4 结 语
笔者利用局部均值分解处理癫痫脑电信号,并对分解的信号进行特征提取,再对所提取特征使用迭代随机森林方法进行分类,完成对癫痫脑电信号的自动检测。实验结果表明,该方法可对癫痫发作期和发作间期的脑信号准确分类,分类准确度高达98.177%,为癫痫的快速准确检测奠定了良好的基础。

