无线电监测中调制信号特征提取算法
李 琳
(青海省无线电管理办公室 海南管理处,青海 海南藏族自治州 813000)
0 引 言
无线电监测是指在无线电管理领域中综合运用各种手段对无线电信号进行检测、搜索和拦截等,并以此为基础对获取的无线电信号进行识别、分析和分解操作,提取无线电信号中的技术参数以及特征的手段。分析信号调制模式,即在当前阶段无法得知信号调制方式的情况下,根据已有的技术手段识别无线电信号调制方式,通过计算与研究得出无线电信号的调制方式。由于对无线电信号调制方式的识别是信号处理领域的重要研究内容,同样也是该领域的研究热点与难点,更是促进无线电信号研究领域发展的基础。
当前无线电信号调制方式识别能应用在无线电信号监测、信号识别和信号认证等多个领域[1]。虽然信号调制识别在理论上取得了重大突破,但是在其实际应用中,由于无线电信号监测环境十分复杂,噪声干扰较大,对无线电信号调制方式的识别造成极大困难,更无法提取到信号调制特征。排除外界干扰因素,在无线电监测过程中准确分析出信号调制方式,提高信号识别率,已然成为信号调制方式识别过程中亟需解决的问题[2-3]。
基于上述分析,笔者重点研究无线电监测中信号调制方式识别算法。构建无线电监测调制信号的数学模型,采用小波变换对调制信号进行降噪处理,结合零中心归一化瞬时幅度之谱密度最大特征提取算法与核判别分析算法,对调制信号进行逐层提取,从而实现各类调制信号的完整分类与提取。
1 无线电监测调制信号的分类
1.1 模拟调制信号
1.1.1 幅度调制信号
采用幅度调制方式得到幅度调制信号,其过程如下式
s(t)=Ac[1+m(t)]cos(2πfct+θc)
(1)
表示。s(f)为刻画幅度调制的程度,可以定义调幅信号的幅度调制指数概念

(2)
根据式(2),得到AM信号的频谱表达式为

(3)
其中M(f)为调制信号m(t)的傅里叶变换,δ(f)为狄拉克函数[4]。由于高频信号受周边环境的影响很大,因此在调幅信号传输过程中可能会出现丢失情况。
1.1.2 抑制载波调制信号
抑制载波调幅信号可表示为
s(t)=m(t)cos 2πfct
(4)
相应的频谱变换式为

(5)
分析式(4)与式(5)可知,s(t)为频率变换后的调制信号,因此该信号中并不具有频谱成分[5]。由式(5)获取单边带幅度调制,计算过程如下

(5)
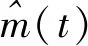
1.1.3 角度调节信号
单位时间内调节信号的次数为

(6)
其中kf表示调频波频率摆动的振幅值,具体表达如下
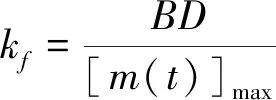
(7)
其中B表示频率摆动的振幅值,D表示最大频偏与调节信号频率的比值。
载频在任何时刻的状态相较于标准状态的偏差值随调节信号的变化值成相关性变化的调节形式,即相位调节
s(t)=[cos 2πfct+kpm(t)]
(8)
其中kp为相位偏移系数。
1.2 数字调节信号
现阶段信息交流设备大多数选用数字调节的方法,较传统调节方法有更多的优点。根据调节方法的特点,通常划分为振幅键控,频率转换键控以及相位转换键控3种。
1.2.1 振幅键控信号
振幅调节信号表达式如下

(9)
其中an表示在时间nTs 数字调节分为多进制调节和二进制调节,其中多进制调节的特征如下:在码元速率相同的条件下,可提高传信率,使系统频带利用率增大。在速率相同条件下,可以降低码元速率。单位时间内数据传输的效率相同时,通过提高各个码元的功能,减轻码元互相干扰的情况[6]。 信号调节的方式之一是把一个周期函数经过傅里叶变换,放在以横轴是频率,纵轴是功率的坐标系上,实现二进制以及多进制信号的解析。 通过以上分析可知,调节信号可以划分为连续谱与离散谱。其中连续谱是指频率在一定范围内由连续成分组成的谱,离散谱是由一系列离散数值的成分所构成的频谱。其中2ASK是通过信号有无进行调制的,4ASK振幅键控信号的特点是在二进制与四进制信号下,将不同频率的振幅最高点连结的曲线,会与瞬时幅值大致相同,同时在码元数值变化的地方幅值变化更加明显,这种特点可辨别调节信号的类型[7]。 1.2.2 频率转换键控信号 频率转换键控是利用两个不同频率F1和F2的振荡源代替信号1和0,传输数据信息控制载频。以2FSK调制信号为例,其相应的频谱为 由式(10)可知,2FSK信号也可以划分为连续谱与离散谱,连续谱是通过双边谱累加得到的,离散谱通常放在载波处。当出现载波差值很小的情况时,例如低于fs,则连续谱会有单峰现象,随着载波差值的不断增加,最终出现双峰。 1.2.3 相位转换键控信号 相位转换键控是一种用载波相位表示输入信号信息的调制技术,其表达方式如下 (11) 其中参量φn是根据随机变量取值的概率规律,从Φ={φ1,…,φM-1}中选值,Δφ表示邻近相位的差值。将调节信号m(t)与载频相乘,获得不同条件下相位转换键控信号。多进制相位转换键控信号的频谱使用效果好、安全性强,是一种良好的数字调节信号。 对2PSK信号进行研究,其功率谱表达式如下 通过式(12)得到,当用一个正的或负的振幅表示其一种状态,接地表示另一状态的数字信号发生等概率现象时,不会产生离散谱。 无线电传输时调制信号将受到周边环境噪声的干扰。对于无线电监测,其重要任务就是要消除周边环境噪声及人为噪声对调制信号传输的影响,在恶劣条件下仍然可以为信号传输与识别的有效性提供保障。在干扰环境中调试信号的表达式如下 (13) 在通常情况下,为使产生的调制信号具有一定的信噪比,需要在调制信号中增加适合的高斯白噪声。信噪比是指在时间意义上的数字调制信号s(t)与高斯白噪声n(t)平均功率的比值,计算公式如下 RSNR=Ps/Pn (14) 在模拟调制信号传输过程中,噪声分离不仅面临的挑战巨大,同时还会随着信号的放大及传输对无线通信造成严重影响,使通信质量下降。在数字通信过程中,信号所携带的信息与脉冲密切相关,只要造成干扰低于设计阈值,在通信信号接收端通过判定信号中是否含有脉冲,就可以保证信号传输的有效性,从而提高无线通信的可靠程度。 在信号处理领域最为常见的信号处理方式是傅里叶变换,而笔者选择小波变换作为无线电信号处理方法,其原因在于调制信号是一种非平稳信号,这类信号的局部性能描述必须以频域与时域信息为基础,才会对调制信号进行精准描述。傅里叶变换在信号处理过程中更为注重全局性[8]。以多分辨率理论为基础,利用小波变换对无线电监测信号进行处理,将其转换为不同子频带集合。对无线电监测信号的高低频处理在不同的子频带分量得以体现。基于上述分析可知,小波变换最大的优势在于将时域信号转换为多个子频带分量总和[9]。正是这种时域信号表达方式上的转变,利用小波分解能使时域信号分解取得重大突破,广泛应用于无线电信号处理领域。 在无线电监测过程中,将任一信号设为s(t)∈L2(R),利用小波变换将其分解为级数形式 (15) 在连续小波变换的情况下,可以将式(15)转换为以下形式 (16) 其中小波系数用cj,k描述,ψj,k(t)表示利用小波变换时域信号进行处理的小波函数。小波变换的基函数为 ψj,k(t)=2j/2ψ(2jt-k) (17) 其中母小波函数用ψ(t)表示,j表示尺度参数,k代表平移系数,则ψ(t)满足下列条件 (18) 其中ψj,k函数的包络与j关系如下:当j>1时,ψj,k函数拉伸,使窗口时宽增加,频率带宽减小;当j<1时,该函数收缩,使窗口时宽减小,频率带宽增大。 在实际应用中,一般情况下将中心频率近似表示为小波频谱能量最多的频率值,将j的取值设置在合理的范围内,可以合理控制信号分辨率。笔者以Haar小波系及Bior小波系为基础选择小波基。 1)Harr小波基函数。Harr小波基函数是最先具有紧支撑集的正小波函数,且使用原理简单,具有非连续性,其表示如下 (19) (20) 2.2.1 基于小波变换的调制信号降噪处理 在对无线电信号监测过程中,特别是在恶劣的环境中,信号发射端在发射信号时将不可避免在其中掺杂有较多的噪声信号,导致在信号接收过程中存在较多干扰,为无线电信号监测过程中的信号调制识别造成了许多困难。所以为提升算法的稳定性,必需先对接收端的信号进行降噪处理。 选取小波去噪系数阈值与噪声信号能量相关,例如在高信噪比的情况下,由于噪声信号所蕴含的能量较小,因此只要选择较小的小波阈值就能实现信号去噪,而在低信噪比的情况下采取的手段则与之相反,在实际应用中阈值的选择可以采用迭代的方式。 2.2.2 小波变换的模极大值算法 在利用小波变换方法处理数字调制信号后,信号幅度与码元相位、频率以及幅度密切相关,其中小波变换的幅值在码元交界处有明显变化,在数字信号调制前后的相位或是幅度之差较大的情况下,就会使码元的变化出现峰值,最后出现周期性边界。数字调制信号经过多次小波分解,随着小波层数的增加,周期性边界与边界突变特征也随之增加,利用这种特性进行数学调制信号与模拟调制信号的划分。对模拟调制信号,其信号幅值并不会出现非连续性变化,但小波变换系数会出现周期性变化,基于这一特点利用小波变化方法分辨模拟调制信号和数字调制信号。 通常在达到一定边界的情况下,才会出现调制信号突变的情况,基于这一特性,设边界条件的阈值M≥0,因此调制信号边界点的产生基于下列条件 1)|cj,k(t0)|≥M; 2)|cj,k(t0)|t0为局部极大值点。 根据分解水平j完成调制信号特征提取 (21) 训练步骤如下: 2)设计边界阈值M,实验样本数据t=1,2,…,T,t满足下列条件: 2.2.3 零中心归一化瞬时振幅之谱密度最大值特征提取算法 通过上述对不同种类调节信号的分析中得到,载波的振幅按照所需传送信号的变化规律而变化,所以会有鲜明的包络现象;但频率保持不变,其幅值不会被影响,所以能当作恒定包络值。因此按照信号的该特点,结合统计方法的性能可区别不同种类的信号。 利用零中心归一化瞬时幅度的谱密度最大值算法进一步获取特征值,公式如下 (22) (23) 区分调节信号的类型。模拟调节信号能分辨出模拟信号所属种类,对数字调节信号,只有ASK信号振幅会受调节的干扰,调相和调频信号都不会发生振幅的改变,换言之,通过谱密度最大值特征方法能分辨出是否为数字调节信号。 2.2.4 基于核判别分析的调节信号特征提取算法 调节形式通过被识别物品和识别装置之间的接近活动,可以自动获取被识别物品的相关信息,这是无线电监测的主要技术手段,通过这种方法分辨出调节形式的类型,是目前较为流行的方法。支持向量机是一种为调节形式提供理论知识的方法,具备完整详细的统计学知识点,对各类数据的解析也具备良好性能。由于支持向量机要经过二次规划过程,导致工作效率降低。核判别辨析算法是核函数和线性Fisher辨别方法相互融合得到的新方法,进一步,假定输入信息数据的数量是n,然后需要对其进行分类,设第i个信息数据为ni。假定空间F内的全部信息数据都选取平均数,φ代表输入空间至特征空间的投影,如果x表示初始特征向量,则φ(x)能当成空间F的输入信息数据。则F空间内求解FDA可转换成寻找最为合适的映射角度w,就是最终目标函数,其公式如下 (24) 其中类内散度矩阵表达式如下 (25) 类间散度矩阵为 (26) 由于对式(24)进行求解的过程较为复杂繁琐,为此通常将其转变成相对更加便于计算和处理的问题。结合再生核理论能明确,在F空间内的所有解w*均为F空间内的数据线性张成,因此有 (27) 其中系数αi为不同样本的权重系数,因此有 (28) 式(28)整理为特征值方程 Mα=λNα (29) 设定最大特征值为λ,相应特征向量为α*。明确α*数值后对数据x在w*上的映射值进行求解,公式为 (30) 于是KFDA的决策函数为 (31) 其中b0表示决策阈值,通常利用L1软边界的SVM值获取。 在KFDA研究算法中,关键步骤是合理地选取核函数,现阶段核函数类型通常为有线性、多项式和高斯径向核函数等。笔者选用第3种方式,如下所示 (32) 其中σ2表示核函数选取数值,x表示核宽度,σ2取值的不同会导致分类结果不同,所以能利用交叉验证方式明确核宽度。 1)初始参数可以划分成训练参数,验证参数和测试参数3种类型。 3)训练公式内的所有参数值,再通过验证参数评判其性能。 4)选取综合性能最好的参数值构建相应序列。 运用核分析算法的过程中,初始参数不能选择最初的信号,因为其信息量较多,同时容易受其他因素的影响,导致KFDA准确性降低。笔者方法利用小波变换收集并整理数据,其中数字偏大的小波系数能保存初始信号的较多数据,所以能更好地保存信息作为初始数据。或将小波系数的高阶统计量设置为测试参数,此方式的优点为其高阶累积量不易受噪声的影响,可以更好地表示初始信号数据。 核判别分析方法的原理为通过判断类间散度判别所属类别。若将数据集划分成3种及以上类别,则需要在此之前修改与完善核判别分析法,通过分解重构算法把多种问题划分成几个二类分类子问题。通过以上分析可知,对数据集进行分解前,要选取最基本的二叉树方式,通常利用此方式进行分解时要遵守由大类数据集到小类数据集的基本要求。 目前调制信号识别方法是电监测领域中的主要研究方向,人们提出了许多思路和方法。通信技术的不断完善,使信号调制种类更加丰富与繁琐,其频带资源也随之减少,导致更加难以实现对调制算法分类器的设计,不仅要提高方法在信噪比方面的准确度,还要降低方法支出成本,以上情况均为需要考虑的重点问题。 笔者研究了目前调制信号类别方法的优势和不足,通过效果较好的小波分析方法,以及核判别方法,较好地实现了利用统计特征算法提取信号的分类特征。同时笔者还将重点放在噪声环境影响下的特征信号提取,引入小波变换方法提升识别的准确度。实验结果证明了所提方法在低信噪比环境下,依然可以实现理想的分类效果,能够实现信号的监测与识别,并及时定位其所在位置,以上均为日后需要研究的重点内容。
1.3 噪声对调制信号的影响
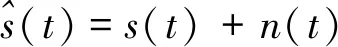
2 调制信号特征提取算法
2.1 小波变换的降噪预处理算法
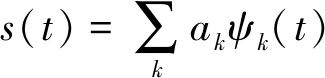





2.2 调制信号的特征提取

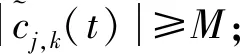

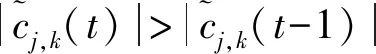








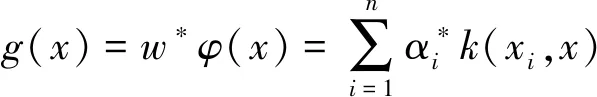



3 结 语

