基于忆阻脉冲耦合神经网络的图像去噪

高宏宇,黄文丽,董宏丽,李佳慧

(东北石油大学 a.电气信息工程学院；b.黑龙江省网络化与智能控制重点实验室,黑龙江 大庆 163318)

0 引 言

在电子工程领域存在4种基本量：电压(v)、电流(i)、电荷(q)和磁通量(φ),以及3种基本电路元器件：电阻R、电感L和电容C。1971年,Chua[1]基于对电路的逻辑性与完整性的理论探索,在理论层面提出了忆阻元件,证明其具有R、C、L等电路元件所不具备的电气特性,并将其命名为电路中第4种基本元件。2008年,HP团队表示其已制造出以纳米环境为前提的半导体材料,即忆阻器实体物件[2]。忆阻元件的记忆属性与纳米级尺寸有望对整个电路理论的变革产生推动作用,并将对计算机、存储器等行业的进一步发展发挥重大作用。为充分发挥忆阻元器件优势,可选用恰当信息处理模式与其结合。例如,将忆阻元件与人工神经网络结合,用其替换原来神经网络的突触更新部分,以获得更好的应用效果。

脉冲耦合神经网络(PCNN：Pulse Coupled Neural Networks)区别于传统的人工神经网络[3],目前已广泛用于图像分割[4-5]、图像去噪[6-7]、图像融合[8]和图像边缘检测[9]等研究领域。笔者把忆阻元件和传统PCNN模型相结合,利用忆阻元件并联的电路关系模拟神经元之间的连接强度,使神经元间连接强度处于动态可变状态。将该忆阻脉冲耦合神经网络(M-PCNN:Memristor-Pulse Coupled Neural Networks)用于图像去噪,实现了网络权值自适应调节。Matlab仿真实验表明,笔者提出的方法在图像去噪方面具有优势。

1 忆阻突触

惠普实验室在2008年完整开发出纳米级忆阻器M(Memristor)[2],其忆阻器的物理模型如图1所示。其中D表示约为10 nm二氧化钛薄膜层,W代表掺杂层厚度,其根据输入激励产生变化电场而改变,与流经忆阻器的电荷量q密切相关。输入正向激励,W厚度增加,M阻值变小；反之,M阻值变大。

图1 忆阻器物理模型结构

鉴于忆阻元件内部二氧化钛薄膜离子的移动状态,可将理想型忆阻器模型阻值表示为

R(x)=RON(x)+ROFF(1-x)

(1)

V(t)=R(x)i(t)

(2)

理想状态下,忆阻元件模型的二氧化钛膜内离子移动呈现线性特性。但实际情况中忆阻器为纳米元件,若输入一个较小信号,则忆阻元件内部发出极大电场效应,膜内离子移动呈现非线性特征。边界移动速度表达式为

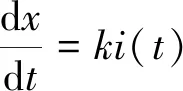
(3)

其中i表示通过忆阻的电流。

为达到效仿这种非线性膜内离子的移动状态,需在式(3)右侧乘以BiolRet窗函数f(x)=1-(x-sgn(-i))2p,得

(4)

图2 I-V滞回曲线

当为忆阻元件两端输入频率f=107Hz的正弦波激励时,忆阻器的V与i关系呈现为过0点的蝴蝶结状滞回曲线(见图2)；若f值继续增加,则曲线会逐渐成为直线,即处于该状态的忆阻器等同于传统模式状态下的线性电阻,该特性证明了此为典型忆阻器模型,且忆阻值表现出开关性质。若脉冲耦合神经网络与忆阻器相联合,需修正与完善PCNN模型。

2 PCNN模型

PCNN模型是以仿效哺乳动物视觉皮层细胞活动为目的的单层神经网络模型[10]。目前,研究人员对PCNN的探索与学习范围不断加大,且其应用于图像处理与模式识别研究均已获得极大进展。PCNN普遍用于处理图像、运动目标识别和通信等研究。PCNN模型[11-12]由Johnson根据Eckhorn模型提出,目前其普遍形式为

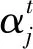
3 M-PCNN模型

传统PCNN模型中神经元间的β数值由人为设置,从而实现数值的改变。参数的固定性会导致图像失真过大或去除噪声不明显,而实际的神经元间连接强度可根据外部输入刺激大小自适应变化。为更有效实现网络的自适应性,笔者在原始PCNN模型上增加忆阻元器件,实现根据输入情况自适应调节神经元间β值,从而使PCNN变为可动态变化的网络,进而实现神经元间β值动态可变。神经元的内部状态由神经元的第N次反馈输入和神经元间连接强度对线性链接输入的影响决定。

笔者选择阈值自适应忆阻器,为其输入矩形波信号,获得阶梯状忆导曲线。若输入激励为0或很小时,忆阻阻值会维持不变状态[13],表明输入恰当的激励电压可使忆阻器维持连接值不变。神经元模型触发周期

(10)

其中τE为阈值的衰减时间常数,VE为输入网络的电压值。

鉴于其与连接强度β值直接影响神经元间点火频率,对网络最后输出结果起决定性作用,因此考虑选用忆阻器并联取代原PCNN模型中的β部分(见图3)。

图3 M-PCNN模型

根据忆阻元件的自身属性可知,忆阻阻值可随输入电流变化而改变。笔者通过将两个忆阻元件反向并联,并考虑掺杂层厚度变化,可推得

(11)

将外输入激励充当忆阻器的控制电压,激励强度影响了忆阻总阻值的改变量,致使β值发生相应的改变。忆阻元件在网络中类似纽带,将神经元之间的连接强度β与外部输入相关联,在维持其他条件不变的情况下,β值与M值变化密切相关。其中β取值根据忆阻函数重新设定。

利用忆阻控制函数f(Mij)表示β值为

β=f(Mij)

(12)

由并联忆阻函数重新表示

(13)

则神经元的触发周期

(14)

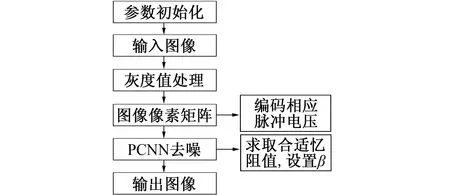
图4 M-PCNN图像去噪流程图

基于以上模型和公式,给出M-PCNN去噪流程如图4所示,该流程图展示的一部分是常规的图像去噪,是输入图像转变为矩阵,直接进行图像去噪处理；另一部分展示的是图像转化为像素矩阵后,矩阵的数值作为相应的脉冲电压,对忆阻器发挥作用,进而影响连接强度对图像做去噪处理。

在图像去噪过程中,传统形式PCNN参数的设定过程比较繁琐,无法有效去除噪声。基于此,笔者提出利用忆阻元件改进PCNN的图像去噪。M-PCNN图像去噪步骤如下：

1)初始化神经元参数,输入测试图像,得该灰度图像矩阵(256×256像素),矩阵中元素为0～255的整数值；

2)利用忆阻元件替换PCNN连接强度部分,图像矩阵中的每个元素对应相应的脉冲个数,并将其编码成相对应的电压脉冲；

3)将脉冲电压输入到忆阻元件中调节控制输入电压,根据忆阻函数求取相应忆阻值,从而取得β值；

4)输出去噪后图像。

4 Matlab仿真结果

4.1 图像去噪效果

用M-PCNN处理添加5%椒盐噪声、30%高斯噪声的Lena图像,并将输出结果与PCNN、中值滤波和均值滤波3种方法的去噪结果进行比较(见图5)。图5a为原始图像,图5d、图5f、图5h和图5j分别为4种方法对椒盐噪声去噪后的输出,图5e、图5g、图5i和图5k分别为4种方法对高斯噪声去噪后的输出。

图5 M-PCNN与PCNN、中值滤波和均值滤波去躁结果比较

从以上Matlab仿真实验可知,M-PCNN去噪效果优于其他3种去噪方法。与中值滤波[14]、均值滤波[15]相比,基于M-PCNN的方法对噪声的滤除效果更佳,不会出现图像大量细节丢失以及失真过大现象。

图6 图像去噪PSNR性能指标

相比传统PCNN,笔者将PCNN模型与忆阻元件相结合构建新网络,可随输入脉冲的变化而不断改变忆阻阻值,以获取神经元间的β值,实现连接强度动态可变,解决了传统PCNN网络的参数不可变问题。从仿真效果可知,基于M-PCNN自适应图像去噪方法对含有椒盐、高斯噪声的图像均实现了有效降噪,提高了图像质量。

4.2 去噪指标分析

为验证所提方法在图像去噪方面的优势,选取峰值信噪比(PSNR：Peak Signalto Noise Ratio)和图像相似度两种指标评估图像去噪效果。峰值信噪比是一种检测图像噪声去除程度的标准。笔者使用折线图直观表现去噪效果(见图6)。结构相似性(SSIM：Structural Similarity)是一种对图像质量评估的全局指标,其测试值位于区间[0,1],值越接近1,则图像质量高。实验数值如表1所示。

表1 SSIM指标

通过应用两种指标评估实验结果可知,处理同一幅含有高斯噪声或椒盐噪声图像时,笔者设计的方法对两种噪声有明显降噪效果,而其他3种方法的降噪效果不够理想。

5 结 语

笔者把忆阻器与传统PCNN相融合,构建了M-PCNN模型,并与PCNN图像去噪方法进行了比较。以经典PCNN模型为基础,增加了并联忆阻器件,实现了连接强度系数的自适应调节,改善了PCNN模型的参数单一不可变性,使PCNN变成一个动态模型,从而提出了神经元间连接强度更新算法,使其更接近生物神经元的特征。同时,该网络比传统PCNN方法更便于参数调节。最后,Matlab仿真验证了M-PCNN用于图像去噪的有效性与实用性。