水利工程建设工程完工概率分析

王 健

(辽宁省朝阳县水利勘测设计队，辽宁 朝阳 122000)

0 引 言

水利工程的工期风险较为突出，且受物资供应、项目资金、技术条件及相关单位等因素的影响，因此有必要科学分析工期风险[1]。近年来，对于水利工程工期风险管理的研究较多，如郭建辉等[2]对水利工程建设进度风险利用AHP-熵值法进行了深入分析；曹吉明等[3]基于工序逻辑关系和风险关联分析，在进度风险评估中提出了以风险链为评价对象的仿真评价法；刘志清等[4]为了对项目进度进行优化，提出了将关联链法利用瓦工概率修正的优化法；黄建文等[5]对网络计划完工概率利用贝叶斯进度网络图进行了计算；闫玉亮等[6]针对心墙堆石坝施工进度风险提出了将BBNs法和ICSRAM方法相耦合的数学模型。然而，现有研究方法并未考虑非关键与关键线路相互转化的可能，仅仅对关键线路的完工概率进行了分析计算。

1 基于PERT和MC法的完工概率模型

采用完工概率分析模型进行工期模拟试验时，应先对各工序持续时间服从的分布进行分析确定，然后对每一工序持续时间运用随机变量抽样技术得到相应的随机数，最后根据网络计划的各工序持续时间确定关键线路和总工期。N次重复试验后，对不同路线在有效模拟中成为关键路线的次数和有效模拟次数进行统计分析，由此确定不同线路在工程项目中的关键度指标，通过对关键线路的方差和线路期望的统计，对规定工期下工程项目的进度风险或完工概率运用概率统计和PERT相关知识进行计算。

1.1 估计工序持续时间分布参数

通常设定工序持续时间在工期风险分析中服从β分布，采用下式作为其密度函数，即：

(1)

其中，a≤x≤b；r>0；s>0。

式中：a、b为决定分布区间的参数；r、s为决定分布形状的参数。

1.2 随机变量抽样

伪随机数μ1、μ2的生成利用Excel中的rand(0,1)函数来实现，针对随机变量的抽样引入MC法中的抽样方式，计算f[a+(b-a)μ1]/f(c)、f[a+(b-a)μ1]和f(c)，为避免复杂Γ函数的计算将β分布的密度函数代入f[a+(b-a)μ1]/f(c)，其表达式有：

f[a+(b-a)μ1]=μ1r-1(1-μ1)s-1/(b-a)

(2)

f(c)=(c-a)r-1(b-c)s-1/(b-a)r+s+1

(3)

通过随机抽样确定每项工作的ti，由此可得到总工期T在网络计划中的一个样本及其对应的关键线路。总工期T的样本空间{Ti}可通过以上步骤的重复计算确定，抽样过程利用Excel计算。

通过比较分析μ2和λ=f[a+(b-a)μ1]/f(c)，若满足λ≥μ2，则t=a+(b-a)μ1；反之则重新抽样生成伪随机数。

1.3 确定路线的关键度指标

将总工期T的样本空间{Ti}按照网络计划中的n条路线划分为n个子区间，通过MC模拟发现各时间段所划分的子区间及其每条线路成为关键线路并不是重合的。设定αi为网络计划中各线路的关键度，其计算式为αi=ni/M，其中ni为M次模拟中子区间i对应路线成为关键线路的次数；M为有效模拟次数，线路工期在N次模拟中不为0的次数即为有效模拟，这也是判别f[a+(b-a)μ1]/f(c)≥μ2成立次数的条件。

1.4 计算工程项目完工概率

采用PERT法中的计算方法为传统的MC法完工概率P计算的常用方法，该方法对完工概率的计算只考虑一条关键线路，计算过程中往往加入路线关键度指标，即：

(4)

若第j个子区间中存在Tp，则上式可简化为：

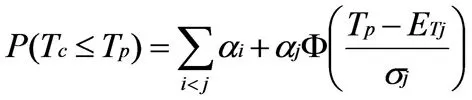
(5)

总体而言，对项目工期风险利用MC法进行分析，其基本流程见图1。

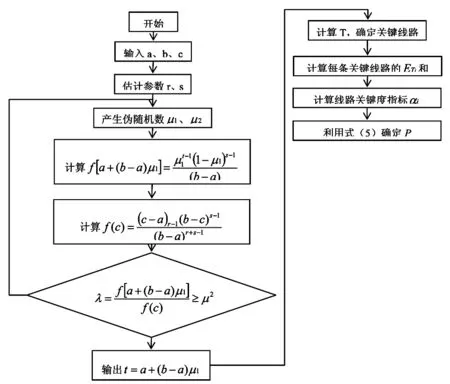
图1 基于MC法的项目工期风险分析图

2 实例分析

图2反映了某水利工程网络进度计划，各道工序在关键线路上的时间参数见表1所示。

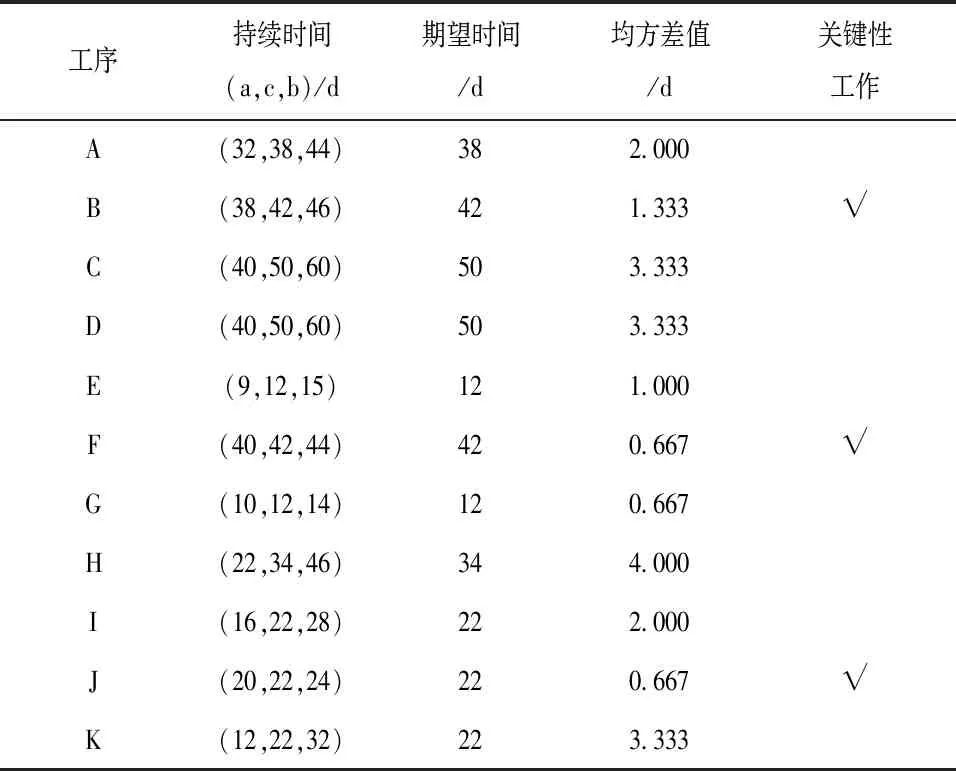
表1 某水利工程各工序方差、期望值、持续时间

图2 进度计划网络

从表1可以看出，B→F→J为关键线路。将各工序持续时间在该工程网络计划中认为服从β分布，则三时估计得到的各工作结果见表1。在满足c=(a+b)/2的条件下，各工序持续时间的β分布参数为r=s=4；设定仿真模拟计算1万次，由此形成μ1、μ2的仿真数。设定f[a+(b-a)μ1]=μ1r-1(1-μ1)s-1/(b-a)，f(c)=(c-a)r-1(b-c)s-1/(b-a)r+s-1，分别计算确定f[a+(b-a)μ1]/f(c)、f(c)和f[a+(b-a)μ1]；然后根据以上计算结果对λ=f[a+(b-a)μ1]做出判别，与此同时完成各工序持续时间tij的输出，模拟结果见表2。

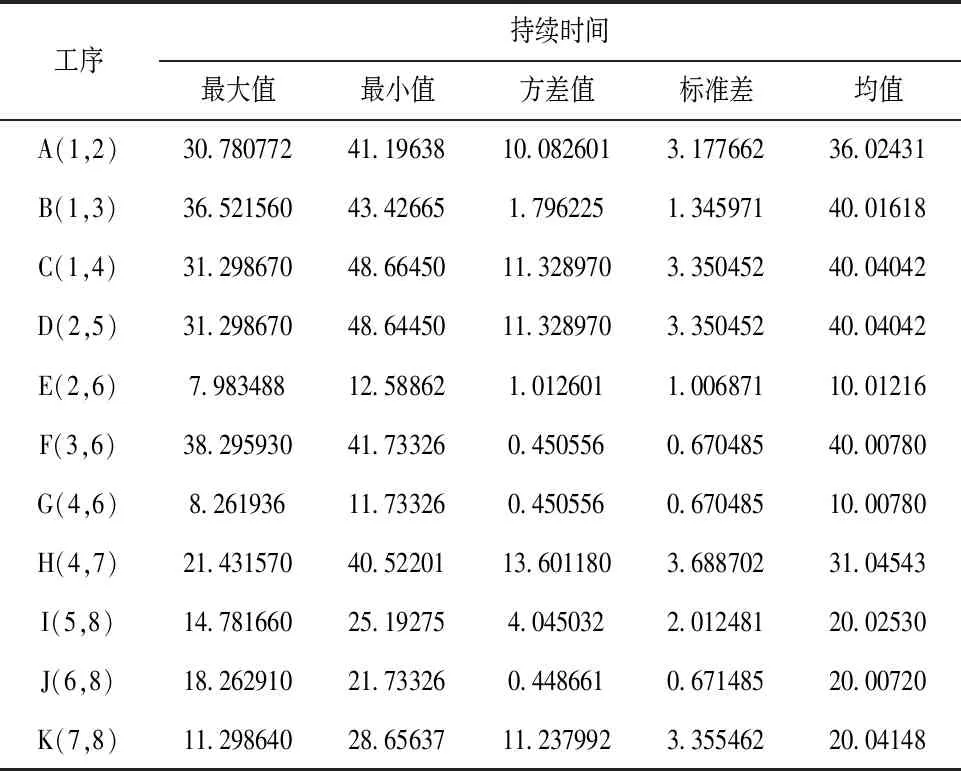
表2 各工序持续时间模拟

可能成为关键路线的路线按照总工期的样本空间Ti计算确定，然后对关键路线的次数及这些路线总工期的方差、均值、最大和最小值进行计算，从而得到管家度指标。该水利工程共有5条路线，经1万次模拟后网络计划模拟结果见表3。

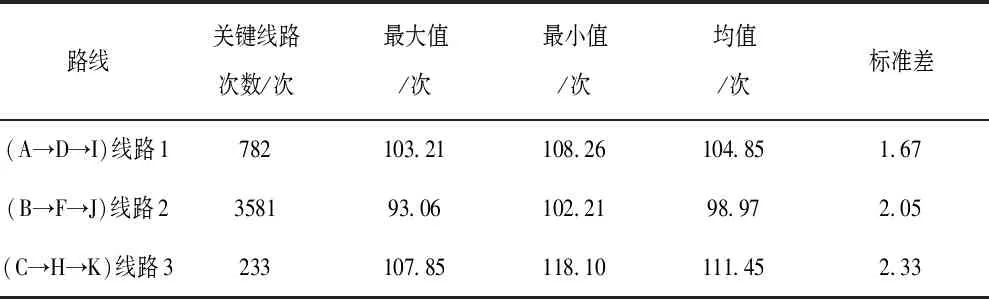
表3 模拟结果

从表3可以看出，有效模拟次数M在1万次模拟中共有4596次，可能成为关键线路的只有A→D→I、B→F→J、C→H→K这三条线路，线路1、2、3为关键线路的次数分别为782、3581、233次，所以计算确定α1、α2和α3值依次为0.17、0.78、0.05。根据其他路线可能成为关键线路的情况以及该工程的计划工期为110d，根据计算公式(5)和MC模型可计算确定：

3 结 论

1)工程实例表明，较传统的MC法文中提出的工期风险分析模型更加贴合实际情况，该方法考虑了关键线路和多条关键线路相互转化的可能，在实践工程中具有较强的适用性和应用价值。

2)相对于计划工期线路5的工期均值偏大，而完工概率在只考虑线路3时有所降低，所以在工期控制过程中要对线路3、5作为重点把控对象。另外，采用Excel软件中自带的函数模拟计算MC法工期计算，在计算过程中因未编制通用程序，因此计算过程略微复杂，未来需要进一步深入研究通用程序的编制。