基于场次临界雨量的小流域山洪灾害多元线性回归动态预警模型研究

王 庆

(凌源市水利工程质量监督站，辽宁 凌源 122500)

1 流域概况

三岔河位于辽宁大连庄河市境内，是庄河市境内的重要河流，发源于西部潘家庄与三东村交界处的南大山，向东南流经该市的三个乡镇，最终注入黄海，全长18.7km，流域面积64.3km2。三岔河属于中温带大陆性季风气候，夏季高温多雨，冬季寒冷漫长。由于研究区位于我国东北地区辽东半岛的东侧迎风坡，因此气候湿润降雨量较大，根据庄河市水利部门的统计资料，当地的多年平均降雨量为974mm。同时，受到气候特点的影响，降雨主要集中于夏季，且多短时暴雨等强降雨天气过程，极易发生流域性暴雨山洪灾害。例如，2017年8月4日庄河市遭遇暴雨袭击，过程降雨量最高达99.1mm，造成流域内山洪暴发，三岔河干流和支流水位暴涨，大量农田被毁，村庄被淹[1]。因此，进行三岔河流域山洪预警研究具有十分重要的意义和价值。

2 小流域山洪灾害场次临界雨量计算

2.1 场次临界雨量的计算方法

山洪灾害是地形地貌、地层特点以及降雨等多种因素相互作用、相互制约的结果，而降雨无疑是其中最重要、最活跃的因素[2]。因此，一个流域发生可能导致山洪灾害发生的临界雨量就成为山洪灾害预警的关键因素和依据[3]。目前，关于小流域临界雨量的计算大都属于静态雨量计算，也就是通过成灾水位确定成灾流量，然后对成灾流量进行反推[4]。同时，利用建立的流域水文模型进行产汇流计算，将获得的最大洪峰流量与成灾流量进行对比，如果相差在允许范围内，则假定雨量即为临界雨量。显然，按照上述计算方法进行临界雨量计算，仅对土壤含水量进行概化，而没有考虑下垫面土壤含水量变化的影响，因此容易导致预警精度不足，产生空报和漏报。同时，由于初始雨量的任意假定也会在成雨量计算结果的误差。

针对上述方法的不足，本次研究中将场次临界雨量作为流域山洪动态预警的样本基础，在临界雨量计算过程中，采取前期降雨确定的土壤含水量进行计算，同时，采用实际降雨量作为计算的雨量输入项，使降雨时程分配符合实际情况，有效避免假定雨型对临界雨量的影响。其具体计算流程如下：截取降雨开始到任意时段T的降雨过程，利用李致家等提出的蓄满超渗兼容产流模型进行流域产汇流计算[5]，并根据计算结果对流域洪水过程线进行推求；与流域的山洪预警流量为指标进行判断，如果推求的洪峰流量大于该指标，说明山洪灾害已经发生，则需要对计算时段T进行重新截取计算，直至推求的洪峰流量小于预警流量；在上述条件下，对T+1时段的降雨量进行从小到大赋值，并对洪水过程进行重新计算，如果此时的洪峰流量大于预警流量，则T+1时刻前的降雨量即为临界雨量；不断重复上述计算过程，即可获取不同场次降雨背景下的临界雨量，并将其作为山洪预警研究的基础。

临界雨量及其影响因素的示意图见图1。其中Ⅰ为前期影响雨量，Ⅱ为预警时刻，Ⅲ为预警时刻前1h的雨强，Ⅳ为临界雨量。因此，计算获取的临界雨量为整场雨的临界雨量。

图1 临界雨量及其影响因素的示意图

2.2 研究区场次临界雨量计算结果

研究中选取三岔河流域内的高阳镇为典型研究对象。根据《庄河市山洪灾害调查成果》，该镇位于三岔河出山口位置，同时也是多条支流的交汇处，属于山洪灾害易发区，其成灾水位为43.51m，预警流量为120m3/s。根据三岔河小流域的实测资料，选取20场具有代表性的降雨，并计算出每场降雨的临界雨量，结果见表1。

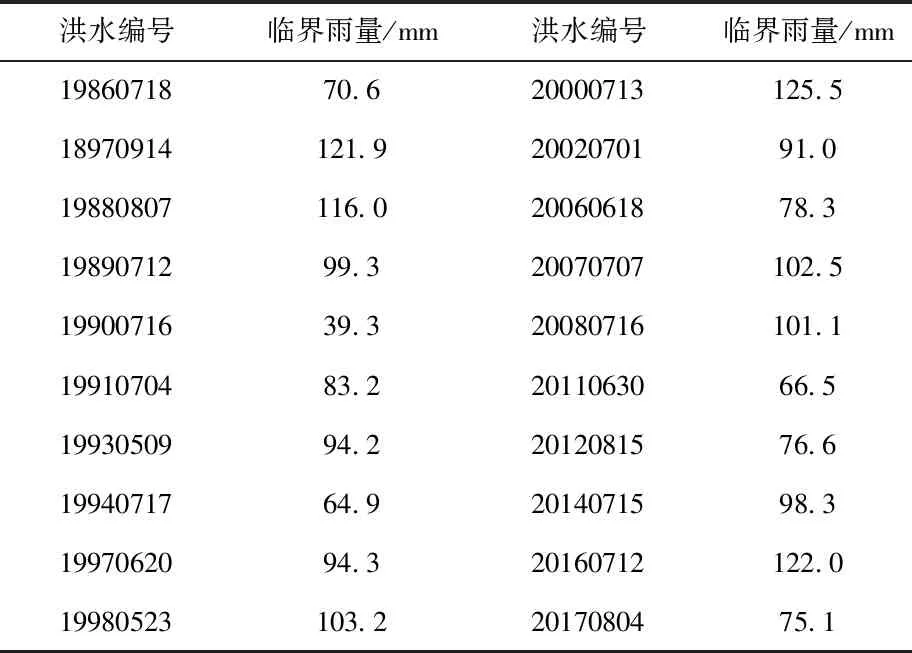
表1 场次临界雨量计算结果

3 山洪灾害动态预警模型

3.1 动态预警数据样本

利用上节计算获取的20场次降雨的临界雨量，分别统计各场次降雨的前期影响雨量、预警时刻前1h雨强以及本场降雨前的降雨量，获得如表2所示的各场次降雨的特征与临界雨量。由表中的结果可知，不同场次的降雨其特征也明显不同，其对应的临界雨量也有所不同。研究中以前14场次降雨作为训练样本，以后六场次降雨为检验样本，构建预警模型。

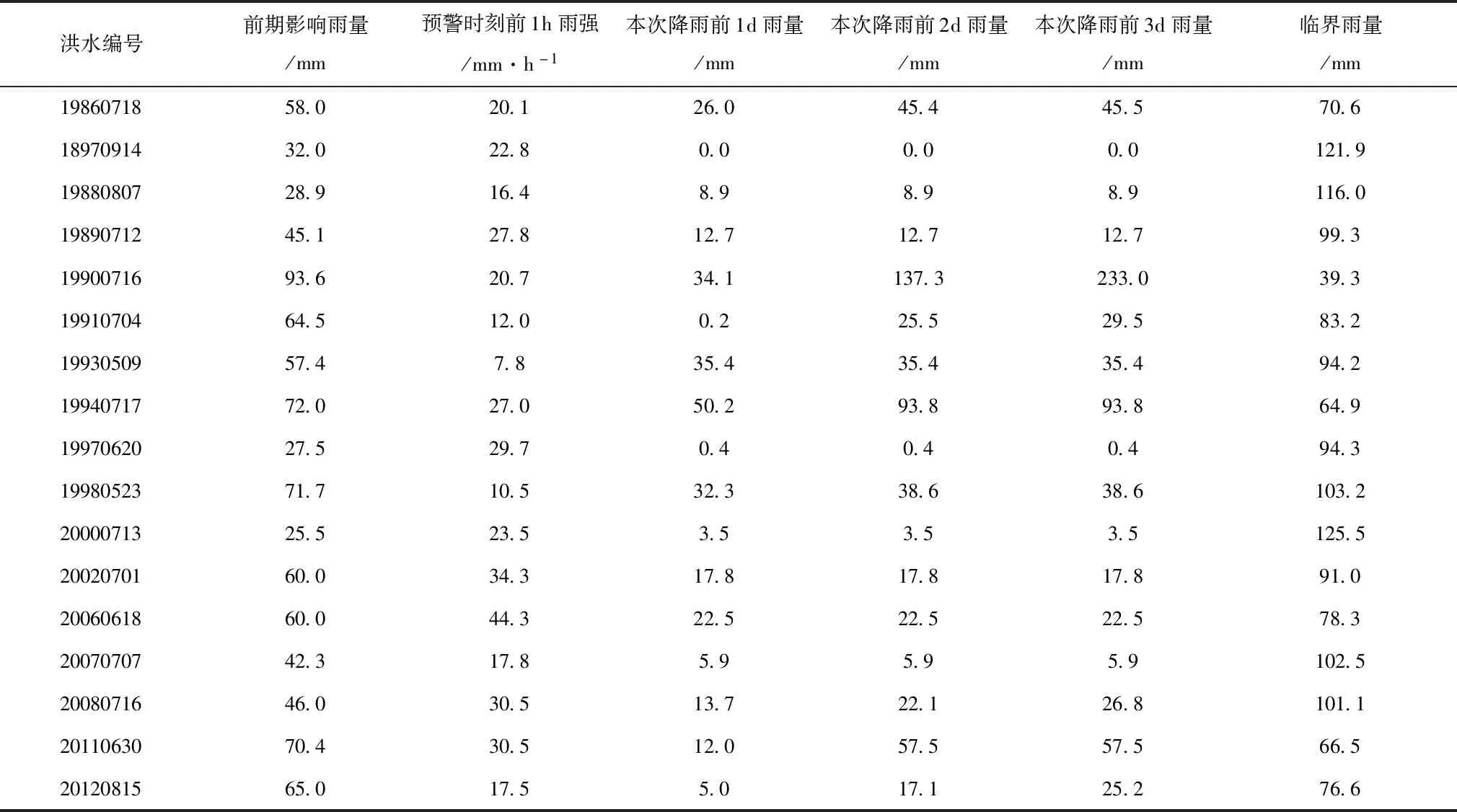
表2 不同影响因素下的临界雨量统计计算结果

续表2 不同影响因素下的临界雨量统计计算结果

3.2 预警模型的构建

多元线性回归模型是一种重要的数理统计方法，主要用于研究一个因变量与多个自变量之间的线性关系[6]。设y为因变量，x为自变量，n组观测值，则有：

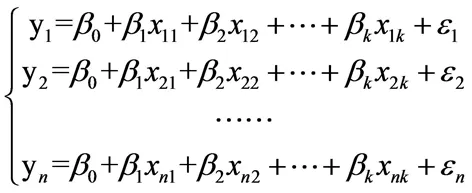
(1)

式中：β0，β1，β2…βk为回归系数，用最小二乘法进行估计，ε1，ε2，…，εn为相互独立的随机误差项。

利用上节获得的数据进行多元线性回归模型的构建，并利用显著性检验、拟合优度等对模型的可应用性进行评价。具体而言，选取表2中前14场次洪水的前期影响雨量、预警时刻前1h雨强、本次降雨前1d、2d和3d的降雨量作为模型的自变量，以场次临界雨量为因变量，利用SPSS软件进行建模计算，获得见表3的建模汇总、表4的显著性检验和表5的回归系数。

表3 多元回归模型汇总表

表4 模型显著性检验结果

表5 多元回归系数结果

由表3中的数据可知，统计量R2为0.976，说明构建的模型具有较高的拟合度，可以解释97.6%的原始数据；由表4中的结果可知，影响因素和临界雨量模型的显著性值为0，小于0.05，说明该模型是显著的[7]。由表5中的系数值可知，多元线性回归方程为：

y=160.506-1.131x1-0.228x2-0.045x3
-0.040x4-0.006x5

(2)

式中：y为临界雨量，mm；x1为前期影响雨量，mm；x2为预警时刻前一小时雨强，mm；x3为本次降雨前1d雨量，mm；x4为本次降雨前2d雨量，mm；x5为本次降雨前3d雨量，mm。

由上式可知，对临界雨量影响最大的是前期影响雨量，也就是前期土壤含水量，预警时刻前的雨强次之。也就是说，土壤越湿润，引发山洪灾害的临界雨量值越小，否则临界雨量值就越大。显然，上述推论也是符合流域产汇流实际情况和规律的。

3.3 预警模型的检验

利用构建的模型对标2中后6场次洪水的临界雨量进行预测计算，结果见表6和图2。从表6的误差计算结果可知，临界雨量的预测误差均在5%以内，从图2可知，模型地拟合结果良好。因此，文章构建的多元回归模型具有较高的预测精度，可以用于研究区的山洪预警。

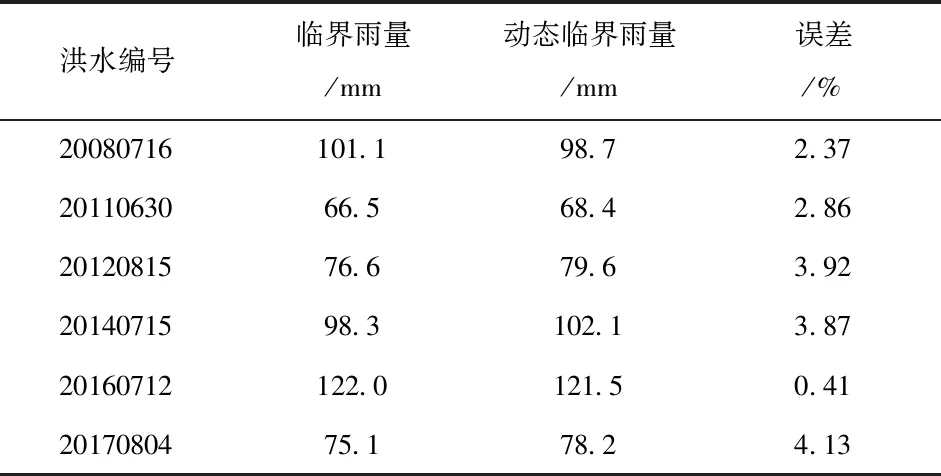
表6 临界雨量的预测结果及误差

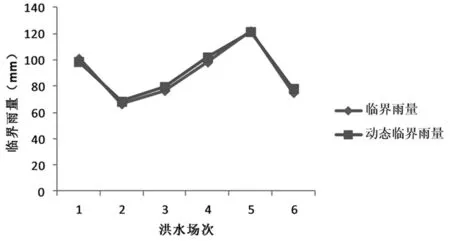
图2 预测样本模拟结果

4 结 语

山洪是山区极为常见的自然灾害，受到特殊气候特征的影响，我国山洪灾害尤为严重。本次研究以辽宁大连庄河市境内的三岔河流域为例，以动态临界雨量计算为基础，构建起山洪灾害动态预警模型，模型的检验结果显示，该模型具有较高的预测精度，可以用于研究区乃至辽东半岛东部地区山洪预警。当然，鉴于临界雨量的不确定性及其对预报预警的影响的复杂性，在后续研究中仍需要在临界雨量的复杂性和不确定性基础上进行临界雨量指标优化，提高模型的预测精度，不断降低山洪灾害预警的空报和漏报率。