土-无柱大跨地铁车站结构地震响应分析
胡双平, 高志宏
(1. 轨道交通工程信息化国家重点实验室(中铁一院), 陕西 西安 710043;2. 陕西省铁道及地下交通工程重点实验室(中铁一院), 陕西 西安 710043)
0 引言
近年来,地铁这一出行方式被越来越多的城市采用,以缓解城市道路交通拥堵问题。地铁车站结构形式也不再局限于传统的有柱岛式地铁车站,多种结构形式逐渐应用于实际地铁建设中,如北京地铁6号线新华大街站采用大跨度Y形钢管柱车站结构[1],青岛地铁保儿站采用无柱拱形结构[2]等。地铁车站作为重要的地下交通枢纽,人流密集,在地震来临时一旦发生结构破坏,将造成严重的人员伤亡及财产损失。
目前,由于无柱大跨地铁车站取消了车站区域的结构柱,能够提高车站的使用空间,保证客流通畅,使车站内部更通透、开阔等,这一结构形式被逐渐采用,学者们也对此作了针对性研究。刘立[3]、林作忠[4]针对国内早期建设的广州地铁2号线无柱地铁车站的结构形式设计难点进行了探讨; 唐小薇等[5]对箱型双层预应力大跨度地铁车站进行了数值分析; 刘明保等[6]、聂永明等[7]以北京地铁亦庄线为工程背景,优选无柱大空间预应力区间结构方案,结果表明所选用的预应力密排框架箱型结构方案安全可靠; 钟波波等[8]采用FLAC3D软件对大跨无柱地铁车站进行了地震响应数值分析; Zhang等[9]建立了水土耦合本构关系; Wang 等[10]采用ANSYS软件,通过改变地震波的入射方向、结构埋深等条件,研究地下结构的响应,得到地震振动方向对地下结构的动力响应有明显影响; Iwatate等[11]、Che等[12]通过1∶30振动台模型试验总结了地下结构在地震作用下的破坏机制,分析得到结构坍塌是由于中柱缺乏抵抗车站顶板破坏后引起剪切变形的承载能力造成的; 车爱兰等[13]进行了相似比为1∶30的模型振动台试验; 季倩倩[14]设计制作了1∶30缩尺比例地铁车站结构模型,进行了国内首次地铁车站结构模拟地震振动台试验,试验结束后地铁车站结构与地铁车站接头结构均未损伤,模型中柱处应变较大; 陈国兴等[15-18]以南京地铁为工程背景,设计并进行了含液化土层的深厚软弱场地基土典型地铁车站振动台试验与区间隧道试验,成功解决了土-地下结构振动台模型试验中土箱的边界效应问题,验证了试验设计的可行性,揭示了地下结构周围土体液化机制,典型地铁车站振动台试验结果表明车站结构中柱应变响应最大,深厚软弱场地基下车站结构侧墙底部应变明显大于顶部应变; 陶连金等[19]以北京地铁为工程背景,进行了大跨度浅埋Y形柱双层地铁车站振动台模型试验,探究其地震响应规律,结果表明埋深增加减小了结构的加速度响应。土-无柱大跨地铁车站相比于传统有柱岛式地铁车站,能够提供宽敞空间,视野开阔,能有效疏导人流,施工速度快以及缩短由于地面大开挖所带来的地上拥堵时间; 但该类结构在地震作用下会受到周围土体、岩体的约束,导致其结构抗震能力较为复杂; 同时,国内外对于地下结构抗震研究理论较少。因此,对于土-无柱大跨地铁车站进行抗震性能研究有深远意义。
本文以南宁地铁5号线金桥站工程为研究对象,对土-无柱大跨地铁车站结构进行振动台试验研究,探究土-无柱大跨地铁车站的地震响应规律及其在地震作用下的薄弱部位。
1 工程概况
1.1 工程背景
本次模拟地震振动台试验以南宁实际项目中的矩形无柱大跨地下地铁车站为工程背景。地铁车站主体段为2层地铁站,采用明挖法施工,总高20.2 m,宽20.2 m; 地下1层净高5.05 m,地下2层净高5.15 m,结构顶板为1.3 m厚的加腋式顶板,中板板厚0.7 m,底板板厚1.4 m; 选取标段总长107 m,两侧有横截面为0.8 m×1.2 m的端部柱,无柱段轴间距长77 m,对此标段进行地震反应规律研究;地铁车站混凝土的强度等级均为C35。地铁车站横截面如图1所示。

图1 矩形无柱大跨地下地铁车站横截面图(单位: mm)
Fig. 1 Cross-section of rectangular column-free large-span underground metro station (unit: mm)
1.2 工程地质条件
根据岩土勘察报告可得地铁车站所选标段的等效剪切波速vse及场地类别,见表1。
表1 矩形结构形式地下地铁车站场地类别判别表
Table 1 Site classification of underground metro station with rectangular structure

试验孔号计算深度d0/m等效剪切波速vse/(m/s)覆盖层厚度/m场地类别JXDX-118.014918.0ⅢJXDX-216.214916.2ⅢJXDX-314.615014.6Ⅱ
由表1可知: 地下地铁车站现场土的计算深度范围内等效剪切波速为148~150 m/s,其算术平均值为149 m/s; 现场土类型主要为软弱土—中软土,且场地覆盖层厚度普遍大于15.0 m但小于50.0 m。结合国家标准GB 50011—2010《建筑抗震设计规范》(2016年局部修订版)和GB 50909—2014《城市轨道交通结构抗震设计规范》相关规定,综合判定南宁地区抗震设防烈度为7度,设计基本地震峰值加速度为0.10g,设计地震分组为第1组,场地类别为Ⅲ类。
2 地震振动台试验
2.1 模型相似比设计
根据地震振动台试验中的模型相似理论,本次试验中为了满足结构模型各物理量间的相似关系,并使重力失真较小,需降低模型材料的刚质比。因此,车站结构模型采用立方体抗压强度为6.66 MPa、弹性模量为6 497 MPa的微粒混凝土制作,在车站结构的顶板、中板与底板分别均匀施加配重70、40、60 kg,共170 kg。车站模型结构各物理量的相似比见表2,车站结构模型如图2所示。

表2 车站模型结构的相似比常数

图2 车站结构模型图
2.2 模型土相似比设计
地铁车站模拟地震振动台试验,其由土-地铁车站结构模型2部分组成,由于土体的最大剪切模量是随深度改变的变量,因此在相似比设计时,不能通过模型结构所采用的相似设计方法进行土的相似设计。本文采用徐炳伟[20]提出的依据土卓越周期相似设计模型土,并以此确定其余物理量的相似关系。
在模型土相似设计试验中,模型土体的等效剪切波速相较于原型场地土的等效剪切波速小很多,本文采用在土中掺加锯末的方法来降低土体的刚质比,设计3种锯末与土的质量配合比,分别为1∶3、1∶5与1∶6,采用动三轴试验得到土体的最大剪切模量Gmax。试验结果见表3。

表3 土动三轴试验结果
试验模型土体厚度为1.2 m,根据文献[12]中规定土的等效剪切波速计算方法,得到各配比土的剪切波速: 锯末土1∶3为18.9 m/s,锯末土1∶5为28.3 m/s,锯末土1∶6为42.6 m/s。为了使模型土的等效剪切波速与原型土相近,根据文献[11]进行对比计算,最终确定结构上部0.28 m土采用1∶5配比土,下部0.92 m土采用1∶6配比土。
2.3 传感器布置
本次振动台试验主要观测土-无柱大跨地铁车站结构在地震作用下的响应,振动台试验传感器布设方案如图3所示。模型结构设置1个主观测面,位于结构正中。图3中,Ax表示加速度传感器沿水平震动方向布置,采集模型体系水平震动方向的加速度; Az表示加速度传感器沿竖向震动方向布置,采集模型体系竖直震动方向的加速度。

(a) 模型地表加速度传感器布置图

(b) 模型主观测面传感器布置图

(c) 模型主观测面整体传感器布置图
2.4 加载设备及方案
本次试验在西安建筑科技大学结构工程与抗震教育部重点实验室进行,采用美国MTS公司生产的4 m×4 m三维6自由度地震模拟振动台,频率为0.1~50 Hz,最大负荷为20 t,单向最大加速度为±1.5g。本试验根据金桥站所在场地特性采用SIMQKE_GR拟合一条满足原场地特性的南宁人工波,天然地震波最后确定选用El Centro波与汶川武都波。各波的地震波时程曲线及傅里叶谱如图4所示。



在确定试验选用地震波后,按主要周期点处各向地震波反应谱谱值加权求和的大小顺序确定地震波输入的先后顺序。依照该方法确定地震波的输入顺序为: 首先为南宁人工波,其次为El Centro波,最后为汶川武都波。试验的加载工况见表4。

表4 地铁车站振动台试验加载工况
3 振动台试验结果分析
3.1 土-地铁车站振动台试验边界效应验证
土-地铁车站振动台试验选用刚性模型箱为模型结构体系提供约束。为尽量还原原型结构在地震作用下的状态,在垂直于振动方向的模型箱箱壁设置了100 mm厚的聚苯乙烯泡沫板,其能减少地震波的反射,较好地还原自由场地震动的输入情况; 在平行于振动方向的两侧模型箱箱壁粘贴聚氯乙烯塑料薄膜并刷涂润滑油,以减少振动方向上的摩擦。
为验证这一处理方法的效果,在工况1下,振动台台面先后输入南宁人工波、El Centro波与汶川武都波,得到模型地基表面平行振动方向测点Ax1、Ax2、Ax3和Ax4的地震加速度时程曲线与傅里叶谱。从中可以看出,模型土体不同位置处的加速度传感器在同一地震波作用下记录的加速度时程曲线十分相似,各测点达到峰值加速度的时间也基本一致。同时,对比各测点加速度反应傅里叶谱,结果表明不同测点在同一地震波作用下的傅里叶谱频谱组成分与谱值接近,说明垂直于振动方向模型箱箱壁所设置的聚苯乙烯泡沫板能消除边界上波的反射与散射,其效果比较理想。
引入相对误差与边界效应指数的概念以定量描述各测点加速度间的离散程度,并验证模型箱边界的处理效果[21-23]。相对误差与边界效应指数的计算方法如下:
(1)
(2)

(3)
式(1)—(3)中:δx,y为相对误差;Sx,y为标准差;μx,y为边界效应系数;xi为距离模型箱箱壁较远位置处的加速度样本值,以该位置处的加速度值为基准值;X为该处测点的加速度峰值;yi为所研究的其他位置处的加速度样本值;Y为对应测点的加速度峰值。
为验证垂直、平行于振动方向模型箱的边界效应,选用Ax1测点的加速度数据作为基准值,以此计算边界效应的各项指标。表5—6示出工况1下,输入南宁人工波、El Centro波与汶川武都波时边界效应验证指标的具体数值。

表5 模型地基表面垂直于振动方向的边界效应验证指标

表6 模型地基表面平行于振动方向的边界效应验证指标
由表5可知,在任意地震波作用下,分析边界效应系数这一验证指标可以看出,距离基准值位置越远,其边界效应系数越大,表现出的总体规律为μ1,4>μ1,3>μ1,2,且边界效应系数均小于10%。有研究表明: 当边界系数小于10%时,模型箱较好地消除了边界处地震波散射与反射。因此,本次试验中垂直于振动方向的模型箱边界具有较好的处理效果。由表6可知,这一规律与验证平行于振动方向上边界效应时得到的规律基本一致。
3.2 模型地基地震响应
3.2.1 输入单向水平地震动
模型地基在水平向地震动作用下峰值加速度随埋深变化如图5所示。由图5可知,在输入加速度峰值较小时,模型地基加速度响应随埋深变化较小; 当输入峰值加速度逐渐增大时,模型地基的加速度响应随埋深变化增大。且下部土层测点Ax31与Ax32之间的加速度变化幅度小于上部土层测点Ax31与Ax3之间的加速度变化幅度。造成这一现象的原因是试验中上部土层选用的试验用土弹性模量低,土层较软,下部土层弹性模量高,土层较硬,上部较软土的地震加速度响应相比于下部较硬土的加速度响应剧烈。

(a) 南宁人工波(b) El Centro波 (c) 汶川武都波
图5 模型地基在水平向地震动作用下峰值加速度随埋深变化图
Fig. 5 Variation of peak acceleration with burial depth of model foundation under horizontal seismic action
3.2.2 输入不同竖向地震动
模型地基全竖向地震动作用下峰值加速度随埋深变化如图6所示。由图6可知,在输入竖向地震加速度峰值较小时,模型地基的竖向加速度响应受埋深影响小; 随着输入竖向地震峰值加速度的增大,模型地基的加速度响应受埋深影响增大,测点间的加速度增长明显大于输入峰值加速度较小时。在南宁人工波与El Centro波作用下,输入不同强度地震时,加速度响应随埋深大致成线性变化; 在汶川武都波作用下,输入峰值加速度较小时,模型地基的加速度响应随埋深大致成线性变化,输入峰值加速度增大后,模型地基表面的放大作用增大,出现明显的折线变化。

(a) 南宁人工波(b) El Centro波 (c) 汶川武都波
图6 模型地基在竖向地震动作用下峰值加速度随埋深变化图
Fig. 6 Variation of peak acceleration with burial depth of model foundation under transverse seismic action
3.3 模型地铁车站结构地震响应
水平向地震作用下,输入不同强度等级的南宁人工波、El Centro波与汶川武都波时,地铁车站结构模型的加速度放大系数随结构高度的变化如图7所示。由图7可知,地铁车站结构模型各处的峰值加速度响应随结构高度的增加而增大,底板最小,中板居中,顶板最大。对于南宁人工波与汶川武都波,随着输入峰值加速度的增加,结构的放大效应呈减小趋势,而在El Centro波作用下的峰值加速度放大系数随输入峰值加速度的增加而增大。在水平向南宁人工波与汶川武都波作用下,车站模型结构的放大系数随输入峰值加速度的增加而有所减小,是由于结构模型在试验过程中逐渐产生损伤,刚度降低,变形能力增强,耗能能力增强,使得其加速度放大系数有所降低。综合土中加速度放大效应所得到的结果可知,土体在南宁人工波与汶川武都波作用下的放大效应也随高度的增加有所降低,考虑结构地震作用是由模型地基传递到地铁车站结构模型,这也是导致这一现象产生的原因之一。在水平向El Centro波作用下,结构模型各处的加速度响应随输入峰值加速度的增加而增大,产生这一现象的原因是: 结构刚度减小,结构整体变柔,此时模型地基的加速度放大效应随埋深减小而增大,致使其对模型结构的作用有所增大,导致结构峰值加速度响应增大,放大系数随结构高度的升高而增大。

(a) 南宁人工波(b) El Centro波 (c) 汶川武都波
图7 车站结构模型在水平向地震动下峰值加速度放大系数随结构高度变化图
Fig. 7 Variation of peak acceleration amplification factor of station structural model with structural height under horizontal seismic action
竖向地震作用下地铁车站结构底板与中板的放大系数如图8所示。由图8可知,除工况2下输入El Centro波时车站模型结构中板的峰值加速度相对于底板有所增大外,其余各工况下模型中板的加速度响应放大系数均小于1,相对于底板的加速度峰值均有所减小。随着输入峰值加速度的增大,中板峰值加速度放大系数相比于输入峰值加速度较小时有所降低,其中南宁人工波作用下中板的峰值加速度放大系数由0.972降至0.830,汶川武都波作用下中板的峰值加速度放大系数由0.882降至0.831。车站结构模型在竖向地震作用下易与土层产生脱开现象,此时模型结构与模型地基无法保持协同作用,模型的加速度响应受自身质量分布与刚度分布影响较大。

(a) 南宁人工波(b) El Centro波 (c) 汶川武都波
图8 车站结构模型在竖直向地震动下峰值加速度的放大系数
Fig. 8 Variation of peak acceleration amplification factor of station structural model with structural height under vertical seismic action
4 振动台试验震后现象
试验结束后模型地基与模型结构的震后损害如图9所示。在试验过程中,模型地基未产生大规模损坏,仅产生局部破坏。试验后将车站结构模型取出,模型车站结构也未产生较大幅度震害,在顶板与侧墙处、中板加腋处产生较多细微裂纹。

(a) 模型地基局部

(b) 顶板侧墙连接处
5 有限元数值分析
采用ABAQUS建立土-无柱大跨地铁车站三维空间有限元数值分析模型,主要采用三维实体单元对土-地铁车站结构振动台试验模型中的各组成部分进行离散。其中,聚苯乙烯泡沫板与模型地基选用三维六面体实体缩减积分单元C3D8R离散,地铁车站结构模型选用三维六面体实体全积分单元C3D8离散,钢筋选用三维两节点桁架单元T3D2离散。网格划分后的有限元模型如图10所示。
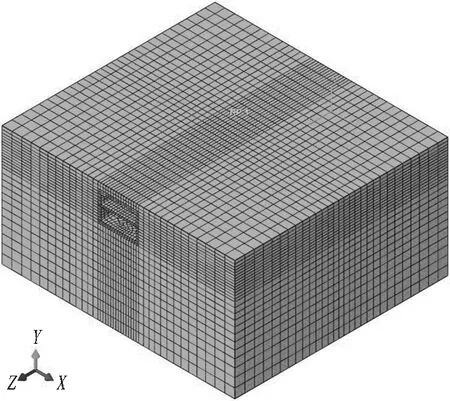
图10 土-地铁车站振动台试验有限元网格划分
Fig. 10 Finite element mesh generation of soil-metro station vibration platform test
5.1 数值模拟结果与振动台试验结果对比分析
在有限元模型中提取对应于测点Ax3、Ax31、Ax32、Ax11、Ax12、Ax13位置处节点的水平加速度响应数据。当输入水平向El Centro波时,数值分析与振动台试验的加速度时程曲线对比如图11所示。
由图11可知,模型体系各位置处有限元数值分析得到的加速度时程曲线与试验记录的加速度时程曲线基本一致。为了定量对比有限元数值模拟与试验结果,采用峰值加速度的差值及差值百分比对误差进行衡量。数值模拟与振动台试验各测点峰值加速度对比见表7。

(a) Ax3 (b) Ax31 (c) Ax32

(c) Ax11 (d) Ax12 (e) Ax13
图11 水平El Centro波作用下数值模拟与试验结果对比
Fig. 11 Comparison between numerical simulation and test results under action of horizontal El Centro wave
表7 水平地震作用下数值模拟与试验结果对比
Table 7 Comparison of numerical simulation and test results under horizontal seismic action

工况测点位置试验结果/(×g)数值分析结果/(×g)差值/(×g)百分比/%E1Ax3埋深0 m0.4450.3830.06213.9Ax31埋深0.4 m0.1760.1780.0021.3Ax32埋深0.8 m0.1470.1410.0064.0Ax11结构顶板0.3680.3300.03810.4Ax12结构中板0.3380.3110.0278.1Ax13结构底板0.2890.2630.0269.0
由表7可知,当输入不同强度的水平向El Centro波时,模型地基与车站结构模型的加速度响应均表现为试验结果大于数值模拟结果,且随着输入峰值加速度的增大,其差值百分比也随之增大。在E1工况下,模型地基试验峰值加速度与数值模拟峰值加速度差值百分比最大值为13.9%,车站模型结构试验峰值加速度与数值模拟峰值加速度差值百分比最大值为10.4%; 当输入峰值加速度较小时,试验结果与数值模拟结果吻合较好,输入峰值加速度增大后,试验结果与数值模拟结果的差值逐渐增大,但最大误差控制在20%左右,数值模拟精度较好。
5.2 模型体系应力响应数值分析
由有限元数值模拟结果与振动台试验结果对比可知,数值分析结果能较为准确地反映振动台试验在地震作用下的地震响应。下面对土-地铁车站结构模型体系在0.169g水平向El Centro波作用下的应力响应进行具体分析。
在0.169g水平向El Centro波作用下,车站模型结构侧墙顶部与底部产生最大相对水平位移时,车站模型结构的应力云图如图12所示。

图12 水平El Centro波0.169g作用下车站结构模型应力云图
Fig. 12 Stress nephogram of station structure model under action of horizontal El Centro wave 0.169g
由图12可知,在输入水平向0.169g峰值加速度时,车站结构模型底板与侧墙交接处、中板与侧墙交接处以及顶板与侧墙交接处的应力集中效应明显,应力值较大。为定量分析车站结构模型在地震作用下的应力响应规律,在车站结构模型侧墙上布置监测点如图13所示。经有限元数值计算,提取侧墙各监测点及板中应力幅值见表8—11。

图13 应力监测点布置图

表8 监测点应力幅值

表9 顶板应力幅值
由表8侧墙应力幅值可知,在El Centro波作用下,顶板与侧墙连接部位以及底板与侧墙连接部位应力响应较大,应力幅值最大处出现在与底板连接的侧墙位置。同时,由表9—10各板中应力幅值分布可知,顶板与中板板中应力幅值较小,在加腋处应力幅值较大,底板在加腋处与板中应力幅值均较大。分析对比车站结构模型各处的峰值应力响应可知,顶板与侧墙连接处及其附近侧墙、底板与侧墙连接处及其附近侧墙、中板加腋处、底板加腋处和底板板中是车站结构的薄弱部位。

表10 中板应力幅值

表11 底板应力幅值
6 结论与讨论
本文以南宁地铁5号线金桥站为工程背景,依据相似理论设计了土-无柱大跨地铁车站结构振动台试验模型,进行了模拟地震振动台试验,并对试验结果进行对比分析。得到主要结论如下:
1)模型箱边界处理上,模型土体不同位置处的加速度传感器在同一地震波作用下记录的加速度时程曲线十分相似,各测点达到峰值加速度的时间也基本一致; 不同测点在同一地震波作用下的傅里叶谱频谱组成分与谱值接近。模型箱箱壁所设置的聚苯乙烯泡沫板边界能消除边界上波的反射与散射,其效果比较理想。
2)对于模型地基,在水平地震与竖向地震作用下,当输入峰值加速度增大后,各测点处的加速度响应均有所增大,且均表现为埋深深处峰值加速度小,埋深浅处峰值加速度大; 在水平地震作用下,较软土层的加速度放大效应明显大于较硬土层的加速度放大效应; 且地基加速度放大效应对地震波有明显的选择性,在竖向地震作用下,试验土体分层对模型地基的加速度放大效应影响小,不同地震波作用对模型地基的加速度响应影响较大,峰值加速度增长对模型地基的放大系数影响较大。
3)水平向地震作用下,地铁车站结构模型各处的峰值加速度响应随结构高度的增加而增大,底板最小,中板居中,顶板最大。对于南宁人工波与汶川武都波,随着输入峰值加速度的增大,结构的放大效应呈减小趋势,而在El Centro波作用下的峰值加速度放大系数随输入峰值加速度的增加而增大,在竖向地震作用下表现为底板的峰值加速度响应大于中板的峰值加速度响应,当峰值加速度较小时,不同地震波作用下中板的放大效应差异明显,随着输入峰值加速度的增加,不同地震波对结构中板加速度放大效应影响较小。
4)震害观测表明: 模型地基发生局部破坏,车站结构模型在顶板与侧墙处、中板加腋处产生较多细微裂纹。
目前仅针对南宁地区金桥站进行振动台试验,后续应继续对无柱大跨地铁车站结构在不同地质条件下的地震响应进行深入研究。

