等效断面支护原理与其应用
郑建伟,鞠文君,张 镇,吴建星,卢志国,伊 康,3,周逸群
(1.煤炭科学研究总院 开采研究分院,北京 100013;2.天地科技股份有限公司 开采设计事业部,北京 100013;3.中国矿业大学(北京) 能源与矿业学院,北京 100083)
随着煤炭资源呈现出“由东向西、由浅入深”的开发态势,井下工作环境恶化,巷道破坏失稳等灾害频发[1-2]。针对巷道围岩的支护问题大量学者已经开展了深入研究,经典的能量支护理论[3]、塌落拱理论[4]等研究成果的提出在一定的程度上较好的解决了部分巷道的支护问题;悬吊理论[4]属于锚杆被动支护的理论性解释,同时在巷道围岩表面施加的U型棚等也都属于被动支护的范畴;加固拱理论和组合梁理论[4]认为锚杆可以促进一定范围内围岩形成共同承载结构;围岩强化理论[4]则一定程度上可以认为是对特定围岩的物理力学特性的优化;松动圈理论[5]认为巷道围岩受应力重新分布出现(类)圈状的围岩松动范围;轴变论[6-8]借助弹性理论阐明了冒落拱的存在和演变,且明确了巷道轴比和围岩稳定性之间的关系;文献[9]从锚杆支护构件的受力及相互之间匹配的角度进行研究提出了“三高一低”的支护理念;关键块体失稳理论[10]强调巷道破坏失稳为渐近发展的过程;蝶形破坏理论[11]借助弹性力学分析并强调了巷道围岩在侧向不等压条件下的受力破坏特征;文献[12-13]提出并分析了极限自稳平衡拱模型;文献[14]分析了矩形巷道顶板的受力特征,提出了巷道等强梁支护理念。
不同阶段相应巷道支护理论的提出代表并指导了行业内巷道支护技术发展,为巷道围岩稳定性控制技术的发展起到了卓越的作用。近年来随着开采环境的复杂化,巷道灾害呈现出多种灾害耦合的链式群发特征[15-17],研究人员越来越重视人工支护与巷道围岩的自承载结构之间的协同支护效应,通过采取不同的支护方法来促进巷道围岩发挥支承能力,但是针对巷道围岩自承载能力的实现机理尚未取得统一的认识。笔者在加固拱理论基础上,结合巷道围岩自组织平衡过程中巷道断面轴比的演变特征,提出等效断面支护原理,借助弹性力学对巷道围岩进行建模来分析了等效断面的受力响应特征,得到巷道所在区域内侧压系数(侧向应力与垂直应力的比值,λ)与巷道围岩内部形成的等效断面的轴比(k)之间的理论关系,且在等效断面支护原理的基础上对现有的支护方法进行了重新解构,对复杂地质及应力环境下的巷道支护设计提出新的设想。
1 等效断面支护原理提出
井工巷道是开凿在地层中的具有一定功能性的开挖空间,巷道开挖后围岩中赋存的自然应力场的平衡态遭到破坏。当巷道局部位置承受的应力超过围岩煤岩体的强度极限便会发生变形破坏,在此渐进的破坏过程中巷道的轴比发生变化,反作用于巷道围岩的应力场分布,最终使巷道围岩处于较为均匀的低位应力环境中,直至巷道破坏不再继续发展,此时巷道的轴比称之为该地质及应力环境下的最佳轴比,这一互馈过程便称之为巷道围岩的自稳(自组织平衡)过程,不进行支护的巷道自稳(自组织平衡)过程中巷道围岩破坏演化过程如图1所示,图1所示的矩形巷道在外部载荷作用下端角(a区域)会出现应力集中而首先出现破坏,然后b区域、c区域、d区域依次发生破坏[18],直到巷道边界(最佳轴比)上的应力不超过围岩的极限强度则破坏停止。因此,在巷道几何断面设计的过程中,如果可以采用最佳轴比的断面,则理论上可以最大限度的发挥巷道围岩的结构承载能力,优化巷道围岩的受力环境。但是,在实际的巷道断面设计过程中需要综合考虑施工难易程度、巷道内设备最大尺寸和巷道用途等多种影响因素,巷道断面的几何形态必须进行一定的妥协,从而导致上述不均匀的较大应力场局部分布特征的出现。
当巷道不进行人工支护时,巷道围岩在一定的条件下经过应力重新分布的作用而逐渐改变轴比达到暂时的平衡态,最终因岩体自身物理属性与外部应力环境的不同而闭合或者长时间处于稳定状态;当采取人工支护系统对巷道进行维护时,人为对巷道围岩施加的支护应力在巷道煤岩体内部扩散会形成一定的应力承载结构,该应力承载结构中煤岩体处于三向受力状态,可以承受较高的外部载荷,而使应力承载结构内部的围岩煤岩体处于低位应力环境中。因此,本文在上述围岩自稳过程中的轴变分析(轴变论)和围岩内部的应力承载结构(加固拱)的基础上提出巷道围岩的等效断面支护原理,即将真实承受外部载荷作用的承载结构的剖面中心线构成的曲面称之为等效断面。文献[8-10]认为在外部双向载荷作用下,巷道破坏后且自稳情况下最终的几何形态可以用具有一定轴比(此时称为最佳轴比)的“椭圆”或者“类似椭圆”来进行刻画,也说明具有最佳轴比的“椭圆状”断面具有良好的稳定性,且给出了对应的物理模型实验的说明。结合上述分析,当等效断面的轴比接近巷道在该地质、应力场环境条件下的最佳轴比时,则充分利用了围岩的结构承载能力,因此可进一步明确巷道合理支护的目的是促使围岩内部形成具有最佳轴比的椭圆状承载结构(等效断面)来承担大部分外部载荷,同时使得椭圆状承载结构上承受的应力基本相等。承载结构的外边界极限为巷道断面上顶底板或者两帮锚杆锚固最大距离构成的椭圆拟合线,内边界极限为巷道断面最小外接椭圆包络线,巷道真实断面称之为内断面,巷道围岩等效断面如图2所示。
2 等效断面支护原理分析
由上述分析可知椭圆形巷道在一定的侧压系数(λ)条件下具有良好的稳定性,因此可以借助解析方法对巷道围岩进行建模,分析巷道围岩内部形成的等效断面(应力椭圆)的受力响应特征,得到一定应力条件下椭圆的最佳轴比(椭圆边界切向应力最小)。首先对巷道围岩进行理想化处理,简化巷道围岩煤岩体的边界条件且认为围岩符合弹性力学的5个基本假设,虽然该解析方法不能直接用来解决具体的工程问题,但可以获得一些有益的认识,对于现场工作的指导有一定的借鉴作用。巷道围岩应力椭圆(等效断面)受力如图3所示。图中ξ0为应力椭圆中心至其边界的距离;θ为研究点与应力椭圆长轴的方向角;σθ(ξ0)为椭圆边界上任一点的切向应力;P0为应力椭圆(等效断面)所承受的垂直应力;λP0为应力椭圆(等效断面)所承受的水平主应力;λ为侧向应力系数,表示水平主应力与垂直应力的比值;A,A′分别为与纵轴的上交点和下交点;B,B′分别为与横轴的右交点和左交点。
借助复变函数和极坐标分析给出了巷道在双向载荷条件下形成的应力椭圆(等效断面)边界上各点的切向应力表达如式(1)[19-20]所示:
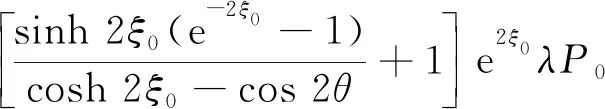
(1)
借助双曲函数、三角函数和指数函数的辅助等式改写式(1)得到
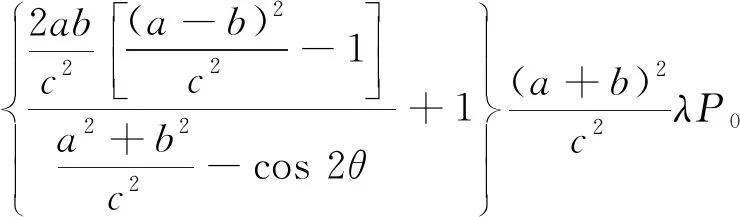
(2)
式中,a为椭圆的长轴的一半;b为椭圆的短轴的一半;c为椭圆的焦距的一半,且c2=a2-b2,将c2=a2-b2代入式(2),可得

(3)
设a=kb,其中k为应力椭圆的轴比(k>0且k≠1),可以得到应力椭圆边界上切向应力表达方程,且可以将σθ(ξ0)看作是关于θ(θ∈[0,2π])的函数,如式(4)所示:
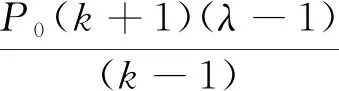
(4)
式(4)两边对θ求导,得出当θ=0,π/2,π,3π/2时σθ(ξ0)可以取极值,即应力椭圆与横轴和纵轴的交点为极值点。因此分别将θ=0,π和θ=π/2,3π/2代入式(4),得出应力椭圆在横轴和纵轴的应力极值σθ(ξ0)(-)和σθ(ξ0)(⊥)分别为
σθ(ξ0)(-)=(2k+1-λ)P0
(5)
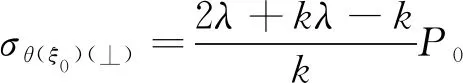
(6)
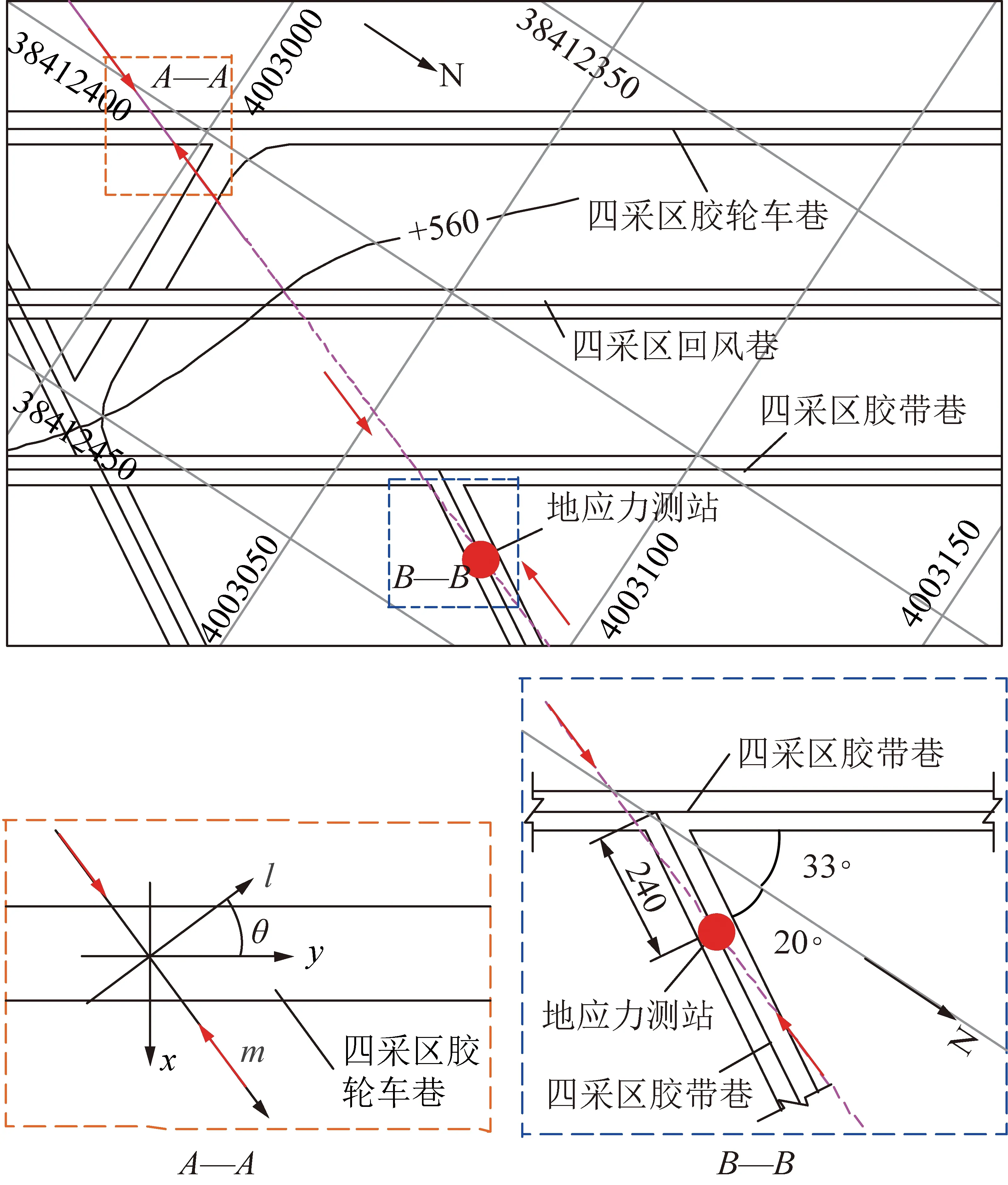
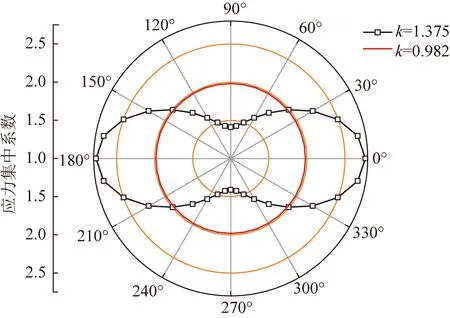
结合图3和式(5),(6),认为当λ>2k+1,应力椭圆边界上切向应力极值点位于纵轴的A点和A′点且均为压应力,横轴的B点和B′点均为拉应力;当k<λ<2k+1,应力椭圆边界上切向应力极值点位于纵轴的A点和A′点且均为压应力,横轴的B点和B′点均为压应力;当k/(2+k)<λ 不同侧向应力系数条件下定常轴比应力椭圆边界上切向应力系数分布特征如图4所示,其中侧向应力系数λ选择旨在定性描述定轴比的应力椭圆在不同应力条件下的演变趋势,假设k=2,分别取λ=0.1,0.3,0.5,0.8,1.8,2,3,4,5,6,8。分析图4可知,当轴比一定的情况下,随着侧向应力系数的增加,巷道顶底板围岩煤岩体由拉破坏转变为压破坏,巷道两帮围岩煤岩体由压破坏转变为拉破坏。 图4 等轴比不同侧向应力系数条件下的应力椭圆边界 应力集中系数分布特征Fig.4 Distribution characteristics of stress concentration coeff-icients in stress elliptic boundary under different stress conditions 煤岩体的抗压强度远大于抗拉强度,令巷道围岩煤岩体的抗拉强度为R,现仅针对纵轴来进行分析,当应力椭圆纵轴的A点和A′点的切向应力σθ(ξ0)(⊥)低于煤岩体的抗拉强度R时,纵轴端部不出现拉破坏,可称之为弱拉应力状态(Ⅱ),如下式 (7) (8) 当应力椭圆纵轴的A点和A′点的切向应力σθ(ξ0)(⊥)=0,可得式(9),即称之为零应力状态(Ⅲ),分析式(9)可知λ=k/(2+k)。 2λ+kλ-k=0 (9) 综合分析应力椭圆纵轴的A点和A′点的3种受力状态:等应力(Ⅰ)、弱拉应力(Ⅱ)和零应力(Ⅲ),在巷道应力优化过程中,应降低巷道围岩所承受的应力等级且避免拉应力出现。基于上述理论分析零应力(Ⅲ)状态实现的条件苛刻(巷道高度远大于其宽度),且为了满足避免拉应力出现的情况,可以认为应力椭圆的理想受力状态为等应力状态(Ⅰ)。 等效断面支护原理是在加固拱理论强调的围岩内部应力拱形承载结构的基础上,借鉴了轴变论分析的巷道围岩自组织平衡过程中巷道断面轴比的演变特征而形成的。本文的研究明确了人工支护的目的是促使围岩内部形成具有一定轴比的“椭圆状”自承载结构,结合上述椭圆最佳轴比的力学分析式(5),(6)给出了合理支护的标准,即促使巷道围岩内部形成的等效断面(应力椭圆)的轴比(k)与巷道所在地质区域内水平主应力与垂直应力的比值(λ)接近或者相等。巷道等效断面支护原理阐明了人工支护促使围岩发挥自承载能力的途径,对于现有支护理念中强调的内容给予新的解释。人工支护的目的在于减少巷道轴变围岩的破坏范围,形成或者增强与侧压系数相匹配的完整的等效断面。可以从以下4个方面来促进等效断面的实现: (1)将巷道所在区域地应力场条件下椭圆的最佳轴比(k=λ)作为确定巷道断面的几何形态和尺寸的考量指标,综合现场工程的实际需要来对内断面的几何形态和轴比进行决策,即在保证巷道功能性的基础上进行巷道断面的尺寸设计时,尽量将巷道断面的内切椭圆的轴比设计为巷道所在区域地应力场条件下椭圆的最佳轴比(k=λ),最大限度利用围岩的自承载能力,保证巷道边界围岩处于较小的应力状态。 (2)在锚杆支护技术中高度重视锚杆(索)预紧力的施加等级,促使锚杆索为巷道围岩提供主动支护力。锚杆预应力场是锚杆杆体端部的螺母扭矩在巷道围岩内部转化形成的,预应力场的范围以及大小与巷道围岩煤岩体的力学性质、螺母扭矩、转化系数、锚杆长度、锚杆间排距有直接关系。通过预紧力等级和其他匹配构件之间的配合,一方面使围岩承受较强的侧向应力而能够提供更高的承载能力,一方面在巷道围岩内形成更合理的预紧力扩散范围,有利于锚杆间应力扩散范围的连接和叠加而形成等效断面;巷道内断面端角部位因端面产生的边界应力的存在而需要补打锚杆(索)来维持顶板与两帮的应力扩散范围的联通,形成完整的应力椭圆;控制巷道断面上锚杆(索)的长度和间排距来调整等效断面的轴比(k),使等效断面呈现出等应力的受力状态(k=λ),如当k<λ时,由式(5),(6)可知,相对于Y,Y′点,X,X′点易出现拉应力,因此可以通过加强两帮的预紧力等级以及增加帮锚杆的长度来实现巷道围岩帮部的应力椭圆的实现,具体的锚杆长度和预紧力等级需根据具体情况来决定。 (3)当巷道处于围岩破碎环境中,在巷道掘进过程中要及时一次支护,后续进行注浆加固,然后再次对围岩施加预紧力;注浆措施可以起到对围岩煤岩体物理改性的目的,增强巷道围岩的强度和完整度,降低锚杆预紧力的损失,有利于预紧力在围岩中的扩散,为巷道围岩范围内的预应力结构的形成提供基础条件;再次施加预紧力是对锚杆因巷道围岩变形而丧失的预紧力的补偿,保证锚杆在围岩内部应力扩散范围的形成,有利于巷道围岩内部椭圆状应力承载结构的重构。 (4)当巷道处于应力较大且特殊地质条件下需要采取全断面支护,封闭式的全断面支护有利于促使巷道围岩内部形成完整的应力椭圆承载结构(等效断面),重视对底板的支护,保证巷道顶板-两帮-底板形成闭环式的应力扩散范围,促使完整的应力椭圆承载结构的形成防止局部区域承载能力不足而导致应力释放出现大的巷道变形。 以山西某矿四采区胶轮车巷为研究对象,该四采区胶轮车巷净断面宽度为5.50 m,高4.00 m,四采区胶轮车巷原支护设计采用“锚杆+锚索+金属网+钢筋梯子梁+喷混凝土”的支护方法来维护巷道稳定。原支护设计方案中顶板锚杆(MSGLW-335/22×2 400)间排距为800 mm×800 mm,帮锚杆(MSGLW-335/22×2 400)间排距为1 000 mm×800 mm,锚索(SKP-18.9×8 300)布置方式为三花布置,金属网采用φ10铁丝编制的经纬网(50 mm×50 mm),钢筋梯子梁(φ14 mm钢筋)宽60 mm顶板及两帮覆盖,顶板及两帮喷射混凝土厚度为150 mm,铺底厚度为300 mm,混凝土强度为C25。但是在原支护设计中没有强调锚杆和锚索预紧力的施加等级,只是采用端头锚固式进行安装,且锚杆及锚索配套采用的托板为低强度普通托板。掘进过程中该研究巷道整体变形量较大,其中巷道发生大量帮臌和顶板小网兜现象。 在研究巷道附近的四采区胶带巷布置地应力测量系统过程中,四采区胶带巷与四采区胶轮车巷的相对关系及监测结果如图5所示,监测结果显示该区域最大水平主应力为9.04 MPa,最小水平主应力为5.22 MPa,垂直应力为8.40 MPa,且最大水平主应力与采区胶带巷夹角为NE20°,与四采区胶轮车巷的夹角为53°。坐标转换[21]如式(10),(11),且σm为旧坐标系下最大水平主应力;σl为旧坐标系下最小主应力;σml为旧坐标系下切应力且σml=0;σx为新坐标系下最大水平主应力;σy为新坐标系下最小水平主应力;θ为坐标系的偏转角度。将地应力的测量结果代入式(10),(11)可得到作用在四采区胶轮车巷两侧的应力分别为σx=8.25 MPa,σy=6.01 MPa,则四采区胶轮车巷的侧向应力系数为λ=0.982。 σmlsin 2θ (10) σmlsin 2θ (11) 图5 地应力测站布置及最大水平主应力方向示意Fig.5 Location of rock stress station and the direction of maximum horizontal principal stress 依据等效断面支护原理分析:该支护设计中未强调锚杆锚索的预紧力等级,因此锚杆、锚索在支护系统中是被动支护的作用,可以认为研究巷道断面设计的轴比k=1.375,大于该区域的侧向应力系数(λ=0.982)。将λ=0.982和k=1.375,k1=0.982代入式(5)和(6),将四采区胶轮车巷的矩形断面抽象为椭圆形来进行分析,得到不同轴比的巷道边界上应力分布如图6所示。分析图6可知,当k=1.375,λ=0.982时,从巷道的整体受力来分析,巷道断面的长轴方向(巷道两帮方向)垂直于巷道围岩的最大主应力方向(垂直应力法施载方向),则巷道的两帮(长轴方向)会产生较大的应力集中系数,形成高度集中应力,同时巷道顶底板的应力集中系数相对较小;从支护角度分析,该支护设计并非最优设计,人为支护系统在支护过程中主要承担被动支护的作用,承载结构(等效断面)轴比大于侧向应力系数,该设计条件下巷道两帮存在发生较大变形的可能性;原设计在顶板布置锚杆和锚索来控制顶板围岩塑性区的离层,当顶板出现离层时,锚杆和锚索会对顶板施加被动作用力,维护顶板的稳定性,此时顶板锚杆受力较大;同理巷道两帮锚杆也会被动向巷道两帮围岩施加作用力,但是帮部锚杆间排距比顶板锚杆间排距大,所提供的作用力较小,不能较好的控制帮部的变形,所以会出现较大的帮臌。巷道实际变形特征如前所述为“少顶板下沉、多帮臌”,与上述理论分析基本一致。 图6 胶轮车巷断面边界应力集中系数分布Fig.6 Distribution characteristics of stress concentration coefficients in rubber tires roadway 如等效断面支护原理所述,建议在支护过程中对锚杆及锚索施加足够的预紧力,使锚杆锚索转变为主动支护,加强对巷道两帮的支护,将帮部锚杆间排距调整为800 mm×800 mm,且安装具有良好匹配性的高强度托板(有利于预紧力在围岩中转化为预应力),使得托板、钢筋梯子梁和金属网等配件之间协调作用,一方面促进单根锚杆在围岩内部形成良好的应力扩散范围,一方面使支护系统更好的形成整体,有利于多锚杆预应力扩散范围间相互叠加而在围岩内部形成等效断面。通过调整锚杆布置位置(巷道端角处补打高预紧力等级的锚杆)和预紧力等级来促使围岩内部形成的等效断面的轴比(k)与该区域内围岩侧向应力系数(λ=0.982)相等或者接近,使得巷道围岩煤岩体承受的外部载荷均匀分布,对巷道的维护起到了有益的作用。 (1)在加固拱理论强调的围岩内部应力承载结构的基础上,综合轴变论得出的巷道围岩自组织平衡过程中巷道断面轴比的演变特征,提出等效断面支护原理。 (2)等效断面支护原理认为人工支护的目的是促使围岩内部形成具有一定轴比的“椭圆状”自承载结构,且将真实起到承载作用的“椭圆状”承载结构称之为等效断面;合理支护的标准是促使巷道围岩内部形成的等效断面(应力椭圆)的轴比(k)与巷道所在地质区域内水平主应力与垂直应力的比值(λ)接近或者相等。 (3)轴比一定的情况下,随着侧向应力系数的增加,巷道顶底板煤岩体由拉破坏转变为压破坏,巷道两帮煤岩体由压破坏转变为拉破坏。 (4)等效断面支护原理可以为现有的支护措施的解释提供新的视角,从理论上进行补充说明,从支护方法选择、巷道内断面设计等方面都有一定的启发:① 在保证巷道功能性的基础上尽量将巷道断面的内切椭圆的轴比设计为巷道所在区域地应力场条件下椭圆的最佳轴比(k=λ);② 高度重视锚杆(索)预紧力的施加等级,在巷道内断面端角部位补打锚杆来维持顶板与两帮的应力扩散范围的联通,形成完整的应力椭圆;③ 围岩破碎条件下的巷道在掘进过程中要及时一次支护,后续进行注浆加固,然后再次对围岩施加预紧力;④ 巷道处于应力较大且特殊地质条件下采取全断面支护,封闭式的全断面支护有利于促使巷道围岩内部形成完整的应力椭圆承载结构(等效断面)。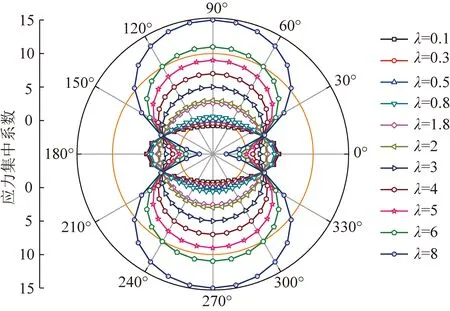
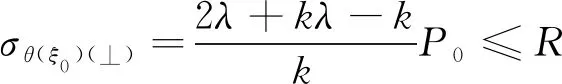
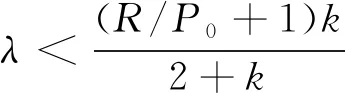
3 等效断面支护原理启发
4 等效断面支护原理应用
5 结 论

