基于锚固力学效应巷道围岩稳定性分析
陈登国,高召宁,赵光明,李顺顺,赵呈星
(1.安徽理工大学 深部煤矿采动响应与灾害防控国家重点实验室,安徽 淮南 232001;2.安徽理工大学 煤矿安全高效开采省部共建教育部重点实验室,安徽 淮南 232001)
当巷道开挖后,围岩初始应力平衡状态发生破坏,在巷道围岩应力重新分布作用下,靠近巷道表面围岩开始进入塑性破坏状态,巷道围岩表面位移也将增大。如果不及时采取有效的支护措施,巷道将会发生变形失稳[1-4]。国内外众多学者对巷道围岩应力分布进行了相关研究,文献[5]把巷道围岩划分为弹性区及塑性区,运用R.Fenner公式对巷道围岩应力分布进行求解,之后KASTNER H对R.Fenner公式作了重要修正。文献[6-8]考虑围岩软化、扩容特性得到了围岩弹性塑性解并对巷道围岩的稳定性进行了分析。而锚杆作为煤矿巷道支护中一种重要的支护结构,众多学者也对在锚杆支护下的巷道围岩稳定性控制做出了许多的研究分析,并取得大量研究成果。文献[9-10]采用现场工程实验、微观结构识别等研究手段得出支护体与围岩在力学特性上的不耦合是造成巷道失稳的主要原因;文献[11-12]通过数值模拟试验建立了考虑初期支护安全性的围岩稳定评价新方法;文献[13]通过数值模拟来验证提高锚杆预紧力对巷道围岩稳定性的作用机理;文献[14]由锚杆与围岩之间的力学效应,采用均匀化方法推导了锚杆支护作用下圆形巷道复合岩体围岩应力分布解析式,并分析了围岩与锚杆的耦合关系;文献[15]通过围岩稳定性评价方法建立了深部围岩与加固体力学分析模型,将锚杆与锚固范围内的围岩形成的复合体等效为共同支护体;文献[16]通过对围岩弹塑性介质中全长锚固锚杆的锚固界面应力分布和变化特征进行分析,揭示了巷道开挖初期支护结构的力学效应对巷道围岩稳定性的影响;文献[17]对预应力锚杆支护机理进行分析,提出通过对锚杆施加高预紧力的方法,提高围岩自身强度,使锚杆与围岩形成自承载结构来维持巷道的稳定性;文献[18]提出了“锚固复合承载体”概念,并推导出锚固复合承载体强度的计算方法。
综上所述,对于现有锚杆与围岩耦合作用的分析通常是将锚杆支护阻力均匀作用于巷道表面,但对于巷道深部围岩来讲,锚杆与巷道深部围岩相互耦合作用会形成承载体,锚杆与锚固范围内的围岩共同维持巷道稳定。为此,笔者在已有研究成果的基础上,基于Mohr-Coulomb准则,在围岩处于极限平衡状态条件下,结合两线段力学模型,研究锚杆支护巷道的力学特性。通过考虑锚杆施加的预紧力结合平衡微分方程计算出锚固承载层范围内的切向应力,并根据静力平衡方程得出围岩在锚固承载层范围内等效支护力的表达式。在该基础上建立了锚杆支护作用下圆形巷道塑性区半径及巷道围岩位移解析解,并对锚杆支护前后圆形巷道的塑性区半径和围岩位移进行了比较,在考虑锚固承载层的条件下分析了锚杆长度、预紧力,间排距对巷道围岩稳定性的影响。
1 巷道围岩力学模型
1.1 巷道围岩受力模型
为便于分析,现假设巷道处于原岩应力为p0的均匀应力场下,巷道围岩为均质各向同性的连续介质,巷道半径为r0,巷道塑性区半径为rp。为分析巷道围岩应力分布及力学特征,巷道围岩应满足以下力学假定[19]:
Mohr-Coulomb屈服准则:

(1)
轴对称条件下的平衡微分方程:
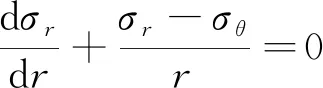
(2)
式中,σθ为围岩的切向应力,MPa;σr为围岩的径向应力,MPa;φ为围岩的内摩擦角,(°);r为距巷道中心的距离,m;c为围岩的黏聚力,MPa。
几何方程:
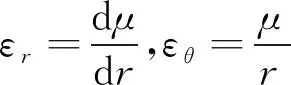
(3)
平面应变问题的本构方程:

(4)
式中,εθ为围岩的切向应变;εr为围岩的径向应变;E为围岩的弹性模量,GPa;ν为泊松比。
对于弹性区(r=rp)围岩的应力
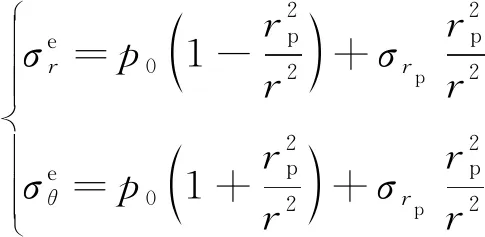
(5)

对于修正的Fenner解在弹塑性交界面(r=rp)时塑性区应力为
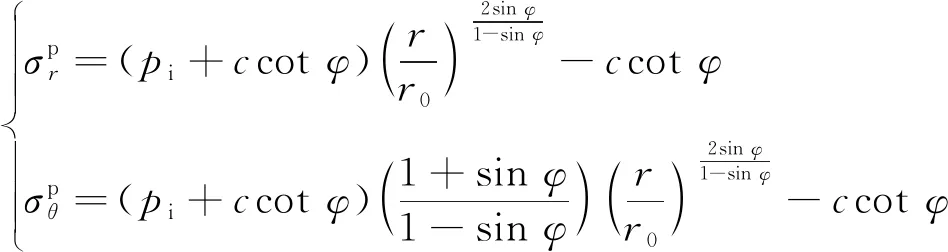
(6)

根据Fenner解的结果:

(7)
巷道开挖后,围岩位移可以表示为

(8)
当r=r0时,巷道壁的位移为

(9)
式中,rp为塑性区的半径,m;G为围岩的剪切模量,GPa;u0(r)为巷道围岩表面位移,mm。
1.2 锚固承载层等效强度参数
为了控制巷道围岩稳定性,常采用锚杆对巷道进行支护。锚杆支护后,锚杆自身不仅能够有效的提高巷道围岩的稳定性,而且由于锚杆与巷道围岩的耦合作用,巷道围岩的自承能力能够得到充分发挥。巷道在锚杆支护下的力学模型如图1所示。图中,lθ为锚杆环向间距;lr为巷道轴向锚杆排距;rm为锚杆横截面半径。本文将锚杆与围岩耦合作用形成的锚固承载层看成均匀的复合岩体,并将黏聚力、内摩擦角、弹性模量作为基本随机变量,由于锚杆与围岩耦合作用下,锚固承载层范围内黏聚力、内摩擦角、弹性模量都将增大,通过参数等效公式并引入锚杆密度因子便可计算得到等效后的复合岩体材料参数[20-21]。
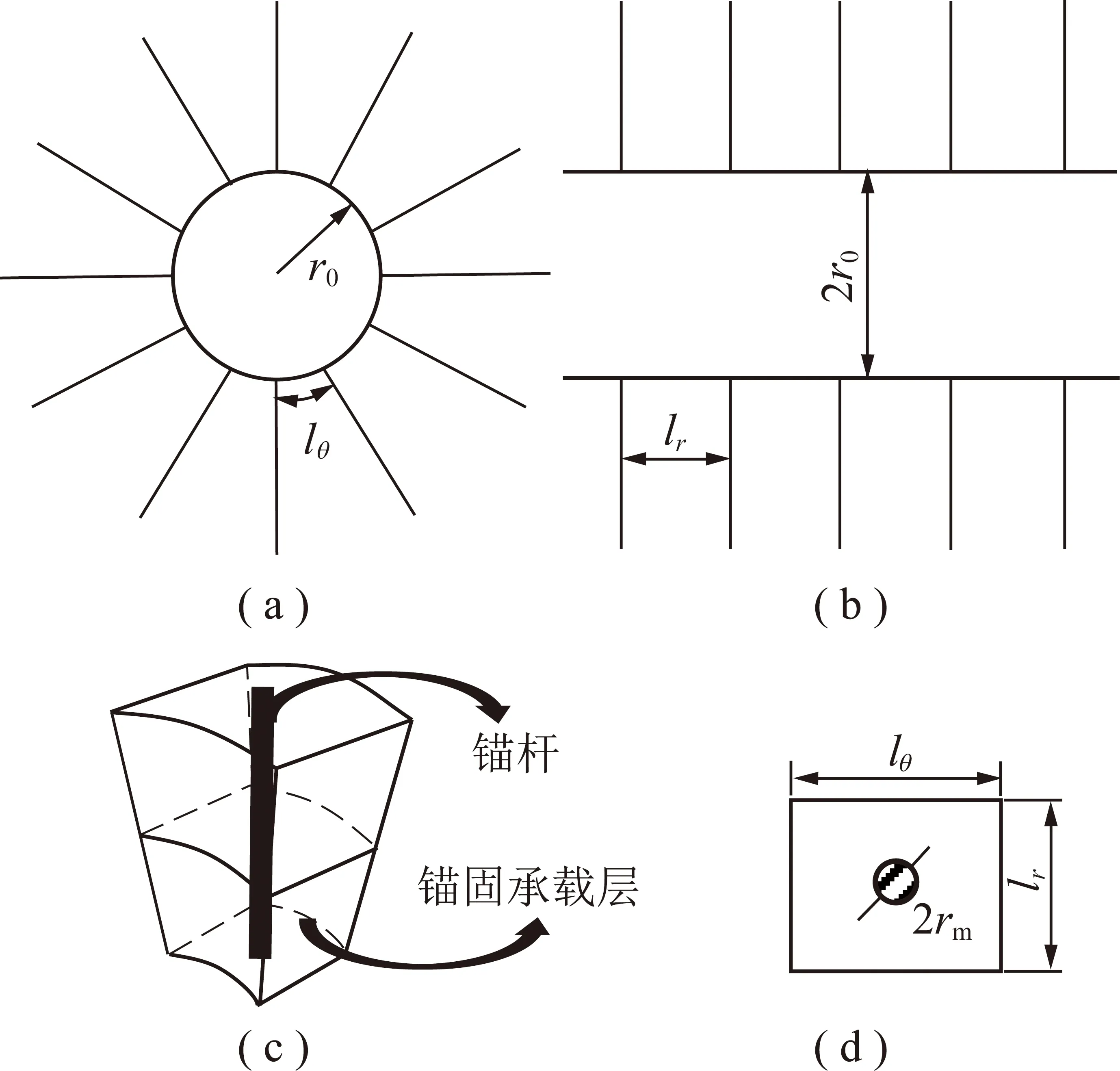
图1 锚杆支护示意Fig.1 Bolt support schematic diagram
锚固承载层的弹性模量是由岩石的弹性模量和锚杆的弹性模量共同影响的,结合图1(c),(d),根据截面积所占比重可以得到锚固承载层范围内的弹性模量:

(10)
即

(11)
式中,E*为锚固承载层等效弹性模量;Eb为锚杆弹性模量。


(12)
式中,f为屈服轨迹梯度;f*为锚固承载层作用下的屈服轨迹梯度;φ*为锚固承载层范围内的黏聚力,MPa。

图2 主应力坐标系中的屈服轨迹Fig.2 Yield locus in principal stress space
影响锚固承载层的强度主要包括锚杆及围岩参数等,其中锚杆参数包括锚杆间排距、锚杆长度L、锚杆横截面半径等参数,围岩参数包括黏聚力,内摩擦角,弹性模量等,这些参数共同影响锚固承载层的强度。考虑锚杆间排距对结构体强度的影响,定义锚杆密度因子α[20]为

(13)
式中,μ为锚杆和岩石之间的摩阻系数,与锚杆表面的粗糙程度有关,使用非螺纹锚杆时,取tan(φ/2),使用螺纹锚杆时,取tanφ。
根据锚杆密度因子的定义,得出巷道支护前后屈服轨迹的关系为
f*=(1+α)f
(14)
屈服轨迹在主应力轴上的单轴抗压强度σc为

(15)
屈服轨迹截距在巷道支护前后的关系[23]表达式为

(16)
结合主应力坐标系中的屈服轨迹(图2)并借助反三角公式得到锚杆支护后锚固承载层的等效摩擦角φ*和等效黏聚力c*分别为
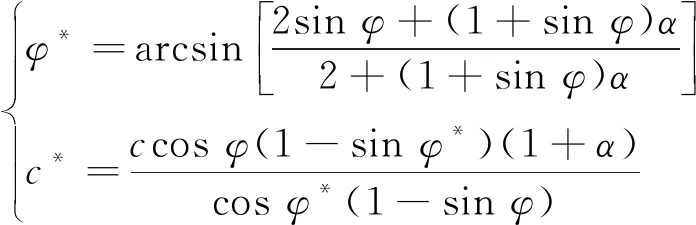
(17)
2 锚固承载层等效力学分析
2.1 锚固承载层等效支护力
相关研究表明[24],在静水压力状态下的水平圆形巷道,当巷道埋深大于或等于20倍巷道半径,此时可忽略巷道影响范围内岩石的重力。当巷道开挖后围岩会发生一定的变形,通常采用锚杆支护提高围岩稳定性。在对巷道围岩进行有规律的锚杆群布置时,通过对围岩的挤压和黏结作用,巷道围岩与锚杆会形成一个承载环。在巷道中的锚杆群布置支护作用下,相邻锚杆之间会形成一个六边形的压密区,由于锚杆之间形成的压密区相互连接,会形成一个连续、稳定的均匀压缩带[18]。压缩带附近的岩体在锚杆支护与预应力作用下处于三向受压状态,围岩强度得到较大提升,从而形成能承受一定荷载的稳定结构,即锚固承载层。锚固承载层受力示意图及其力学模型分别如图3,4所示,其中,pi为围岩均布力下的初始支护力,MPa;r1为围岩弹性区到巷道中心的距离,m。
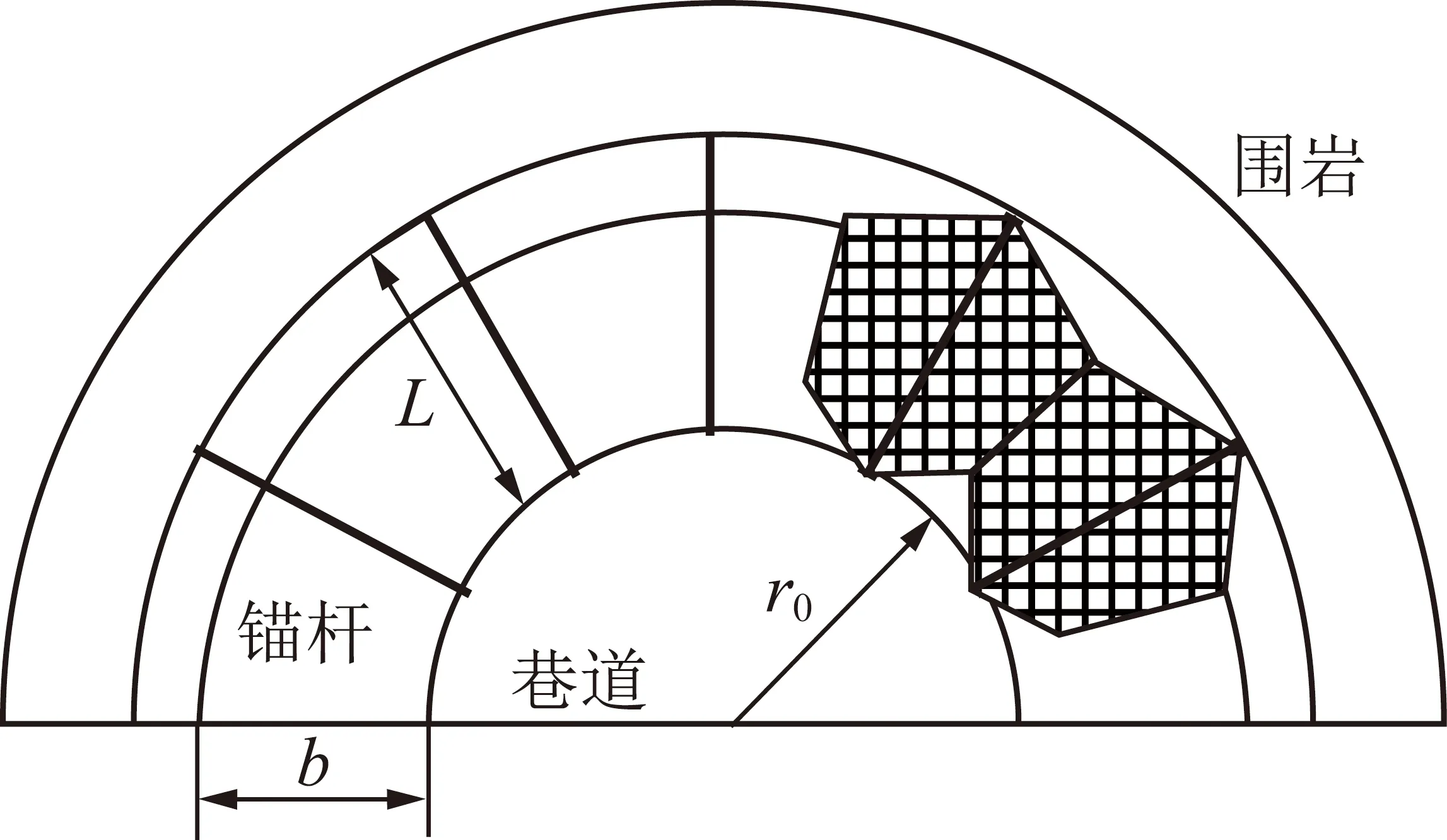
图3 锚固承载层受力Fig.3 Force diagram of anchorage bearing layer
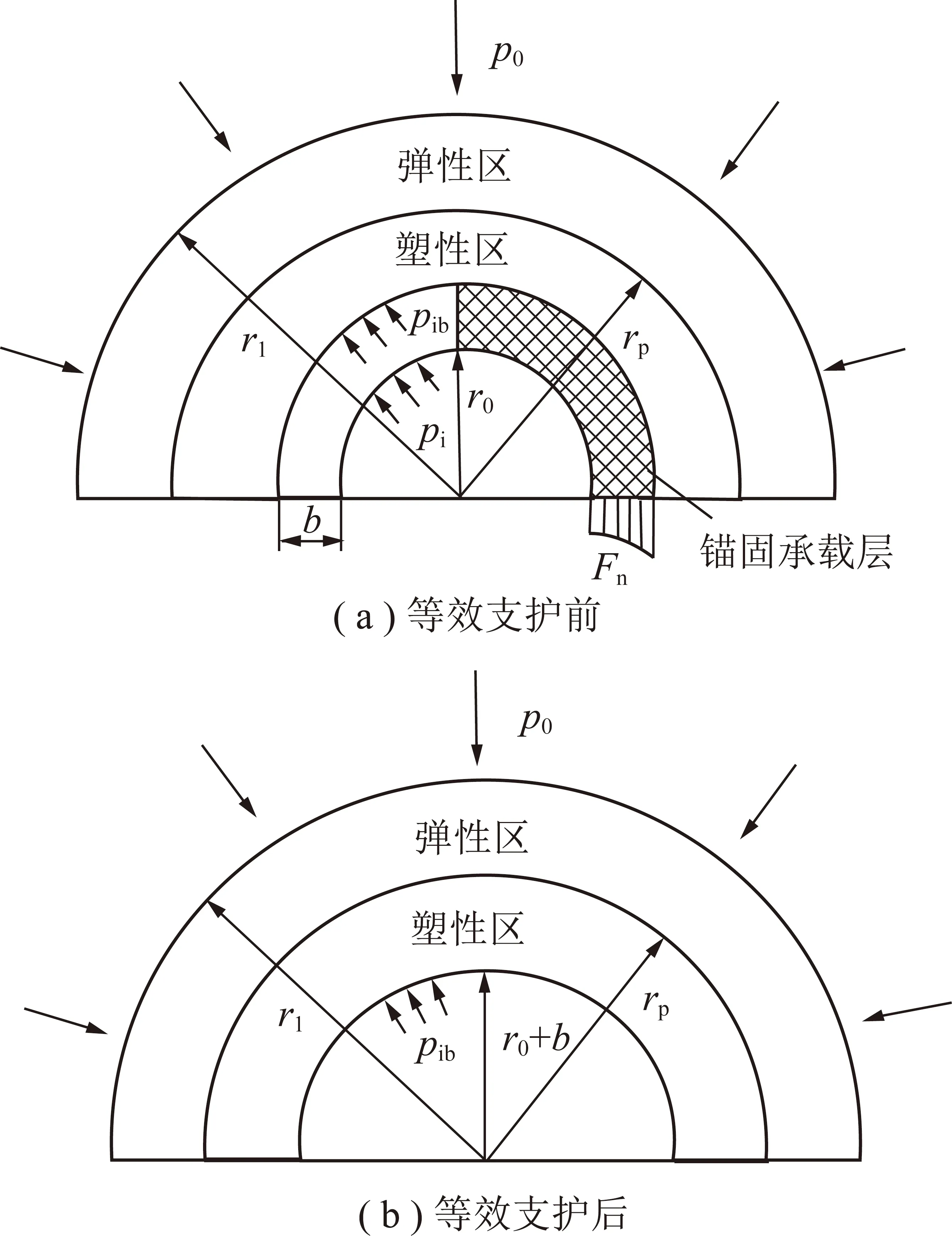
图4 锚固承载层力学模型Fig.4 Mechanical model of anchorage bearing layer
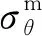

(18)
假设锚固承载层在外载荷作用下处于极限平衡状态,根据Mohr-Coulomb准则并结合锚固承载层沿巷道表面垂直方向上的静力平衡方程,可推导出锚固承载层外边界所能提供的支护强度[13],即锚固承载层等效支护力pib的计算公式:

(19)
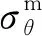

(20)
半横截面锚杆的根数N为

(21)
锚杆支护强度计算公式:
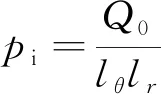
(22)
式中,Q0为锚杆的预紧力,kN。
2.2 锚固承载层的体积力模型及应力分析
本文假设锚杆完全处于巷道围岩塑性区,将对全长锚固锚杆施加的预紧力看成容重f(r),并假定其在围岩中均匀分布,全长锚固锚杆在巷道断面上呈轴对称分布,塑性区范围内锚杆受力示意图如图5所示,其中,Q(r)为锚杆轴向力,kN。

图5 锚杆受力示意Fig.5 Bolt stress diagram
对全长锚固锚杆施加的预紧力为Q0,取锚杆上一微段的厚度dr的单元体,假设锚杆与围岩之间是一个整体且没有产生相对滑移,锚杆预紧力Q0沿锚杆长度方向呈线性分布,根据锚杆微单元体的力学[25]平衡条件可得

(23)
式中,Q0(r)为预紧力Q0引起的锚杆轴力,kN。
此微段的容重dFV为

(24)
则在施加预紧力条件下全长锚固锚杆径向容重可表示为
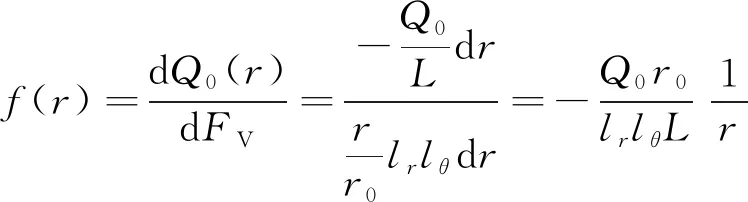
(25)
锚固区范围内围岩应满足:

(26)
由Mohr-Coulomb屈服准则,在极坐标中锚固承载层的切向应力σθ满足:

(27)
联立式(26)可知
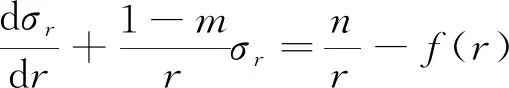
(28)
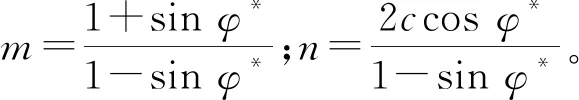
式(28)为一阶线性微分方程,由非齐次线性方程的解可得

(29)
结合边界条件在r=r0时,σr=pi,可得锚固区的应力

(30)
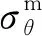
可以求得
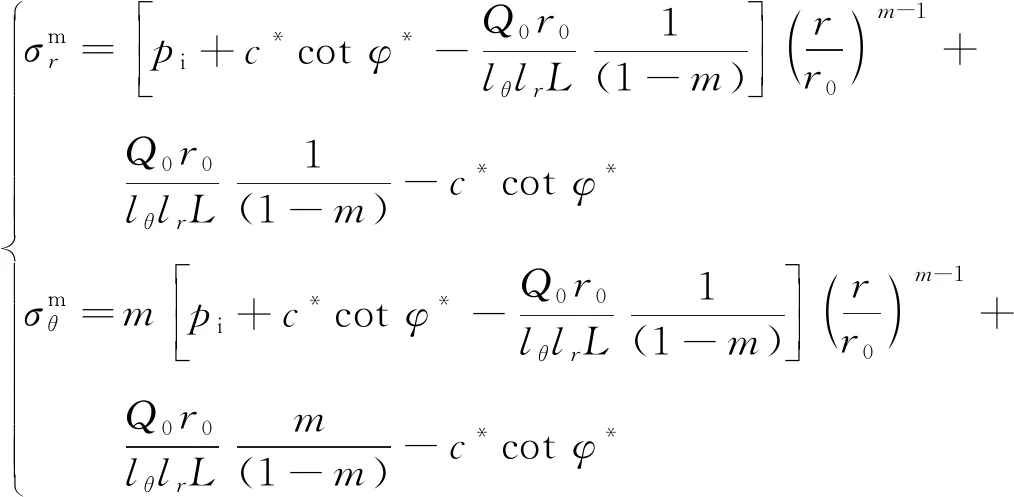
(31)
由式(19)可得

(32)
3 等效巷道力学参数
锚杆和围岩耦合作用下形成的锚固承载层实质上是支撑巷道深处围岩的承载结构,因此可将圆形巷道内的支护阻力pi转化为等效支护力pib,同时巷道半径也由r0转化为r0+b:
(33)
式中,rpib为锚固承载层作用下的塑性区半径,m。

(34)
当r=r0时,巷道围岩表面位移为

(35)
巷道围岩塑性区应力分布可表示为

(36)
4 算例分析
为了进一步研究锚固承载层对巷道围岩稳定性分析的影响,现进行算例分析。假设某圆形巷道埋深532 m,巷道半径r0=3 m,原岩应力p0=12 MPa,弹性模量E=2.6 GPa,泊松比ν=0.3,巷道围岩黏聚力c=0.6 MPa,内摩擦角φ=35°;锚杆直径=32 mm,锚杆长度L=2.2 m,围岩与锚杆间的摩阻系数μ=0.7,lr=800 mm;lθ=800 mm,锚杆预紧力Q0=75 kN,由上述参数代入式(20)可得锚固承载层厚度b约为1.5 m,将上述参数代入式(17)可得锚杆与围岩共同作用下的相关参数见表1,由式(22)可计算出初始支护阻力pi为0.118 MPa。由式(32)可得等效均布力形式下的等效支护力pib。
表1 围岩物理参数
Table 1 Physical parameters of surrounding rock

围岩参数数值锚固承载层参数数值E/GPa2.6E*/GPa2.76c/MPa0.6c*/MPa0.631φ/(°)35φ*/(°)37.5
4.1 锚固参数与锚固承载层厚度的关系
为了分析锚杆预紧力对锚固承载层厚度及等效支护力的影响,现设置锚杆预紧力Q0分别为50,75,100 kN,并结合以上参数代入式(19)可得到不同锚杆预紧力与锚固承载层厚度,等效支护力的关系曲线,如图6(a)所示。由图6(a)可知,在同一锚杆长度和间排距下,当预紧力不同时,随着预紧力的不断增大,所对应的等效支护力明显增加。
为研究锚杆间排距对锚固承载层厚度及等效支护力的影响,现设置锚杆间排距分别为600 mm×600 mm,800 mm×800 mm,1 000 mm×1 000 mm,并结合表1参数代入式(19)得到锚杆间排距与锚固承载层厚度、等效支护力的关系曲线,如图6(b)所示。由图6(b)可知,锚杆间排距也对等效支护力有着明显的影响,随着锚杆间排距的减小,相同的锚固承载层所对应的等效支护力增大。为了分析锚杆长度对锚固承载层厚度及等效支护力的影响,现设置锚杆长度L分别为1 800,2 200,2 600 mm,结合表1参数代入式(19),得到锚杆长度与锚固承载层厚度、等效支护力的关系曲线,如图6(c)所示。由图6(c)可知,锚杆长度直接影响锚固承载层的厚度,锚杆越长,锚固承载层厚度越大,所对应的等效支护力越大,但锚杆长度相较于预紧力以及锚杆间排距对锚固承载层厚度影响较小。由此可知锚杆的预紧力、间排距和长度对围岩稳定性有一定影响,可根据工程实际情况来确定锚杆参数,达到最佳支护效果。
4.2 等效支护力对巷道围岩稳定性的影响
为研究Fenner解与本文解下等效支护力对巷道围岩表面位移的影响,将上述参数代入式(32),(35)可得围岩表面位移与等效支护力的关系曲线,如图7所示。当考虑全长锚固锚杆和围岩耦合作用下形成的锚固承载层时,锚固承载层厚度范围内的等效摩擦角φ*、黏聚力c*以及弹性模量E*相比原参数都会增大,锚固承载层范围内岩体强度明显提高。
由图7可知,等效支护力pib与巷道围岩位移呈负相关,本文解的整体位移量比Fenner解的整体位移量明显减小,从图7中计算可得本文解的巷道表面位移相比于Fenner解下的巷道表面位移减少了39.81%~49.08%,因此在实际锚固支护设计时应当考虑锚固承载层的力学特性,充分发挥锚杆和围岩的耦合作用,提高巷道围岩的承载能力,对巷道的稳定性更加有利。
结合式(33)可得塑性区半径与等效支护力pib的关系曲线,如图8所示。由图8可知,等效支护力pib与塑性区半径关系呈负相关性。在Fenner解下的应力解与本文考虑锚固承载层的应力解相比,由于忽略锚杆和围岩共同作用下形成的锚固承载层,二者塑性区范围的偏差较大。随着等效支护力pib的增加,二者的巷道围岩的塑性区范围都在减小,本文解的塑性区半径相比于Fenner解下的塑性区半径减少了17.71%~20.51%。可以看出锚杆与围岩耦合作用下形成的锚固承载层对于塑性区范围的发育有一定抑制和约束,因此锚固承载层对维护巷道围岩稳定有重要作用。
根据式(5),(36)可得巷道围岩应力分布曲线图,如图9所示。由图9可知:本文解相对于Fenner解巷道围岩的切向应力明显提高,且应力峰值位置向巷道壁发生转移,塑性区范围减小,应力峰值点略有升高。由于锚固承载层的存在,巷道浅部围岩的力学强度明显增强,应力传递受到抑制,在塑性区附近发生应力集中。

图9 巷道围岩应力分布曲线Fig.9 Stress distribution curve of surrounding rock of tunnel
在巷道围岩弹性区内本文解相对于Fenner解的切向应力明显降低,而径向应力始终比Fenner解的径向应力高,随着距巷道距离的增大,逐渐趋于原岩应力。从分析中可知锚固承载层的存在提高了巷道围岩的承载能力,巷道稳定性得到提高。
4.3 锚杆参数对巷道围岩稳定性的影响
为分析锚杆预紧力对巷道围岩位移以及应力的影响,并结合以上参数且锚杆间排距和长度取定值代入式(5),(34),(36)得到锚杆预紧力与巷道围岩位移以及应力关系曲线,如图10所示。由图10可知,随着全长锚固锚杆预紧力的增大,巷道围岩稳定性有着明显提高,同时巷道围岩变形减小,在塑性区内全长锚固锚杆预紧力越大,巷道围岩切向应力明显提高,且应力峰值位置向巷道表面转移,巷道周边围岩的切向应力略有增加。
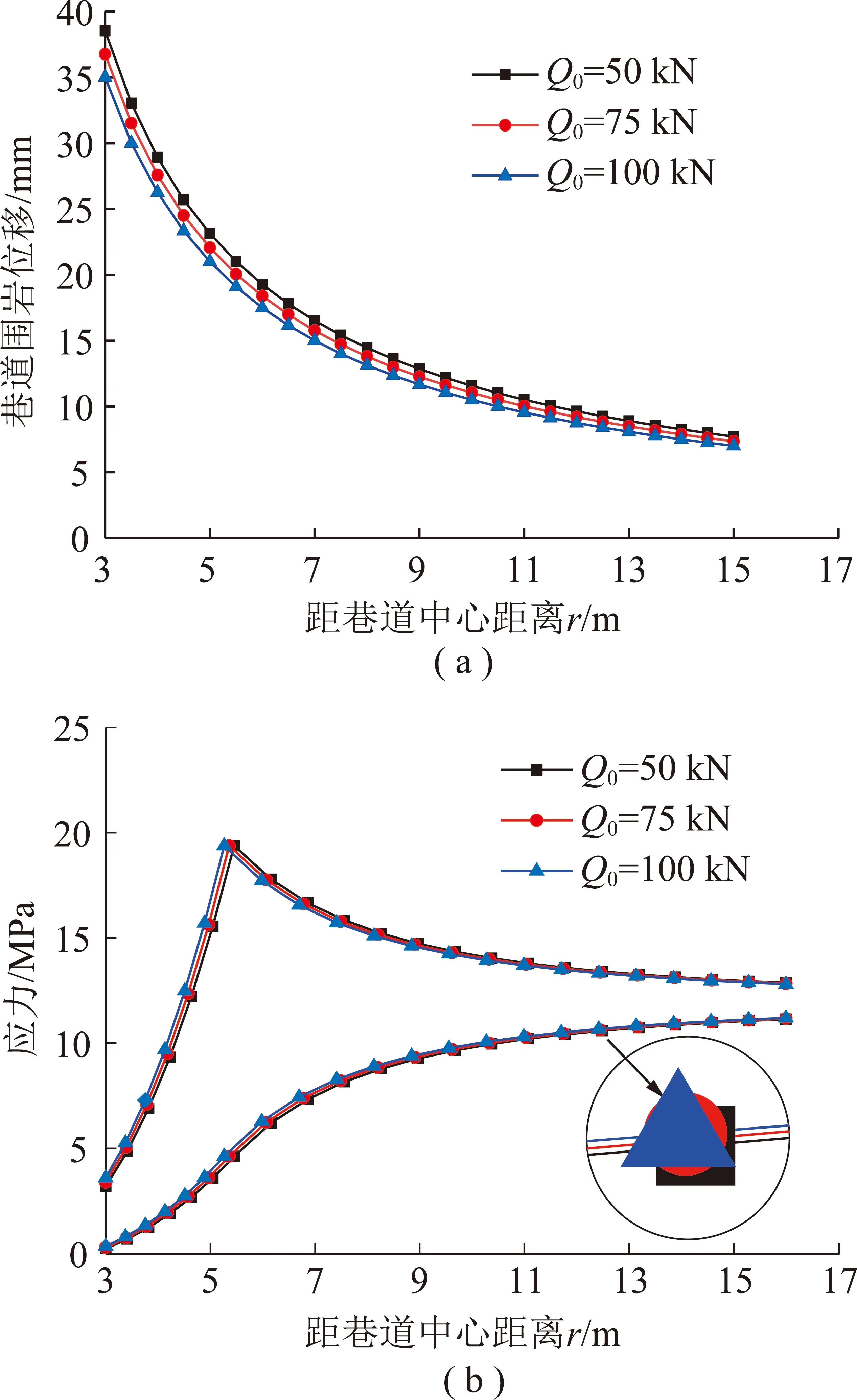
图10 锚杆预紧力对巷道围岩变形和应力的影响Fig.10 Influence of bolt preload on surrounding rock deformation and stress of roadway
为分析锚杆间排距对巷道围岩位移以及应力的影响,并结合以上参数且锚杆预紧力和长度取定值,代入式(5),(34)和(36),得到锚杆间排距与巷道围岩位移以及应力关系曲线,如图11所示。从图11中曲线可以看出,增大锚杆间排距对巷道围岩的稳定性是不利的,距巷道壁相同的距离位移量明显增大,巷道围岩变形明显。从图11中可以看出,在塑性区全长锚固锚杆间排距越小,围岩中切向应力明显提高,应力峰值随着锚杆间排距的减小略有升高,而且向巷道表面转移,巷道周边围岩的切向应力增大。

图11 锚杆间排距对巷道围岩变形和应力的影响Fig.11 Influence of bolt preload on surrounding rock deformation and stress of roadway
为分析锚杆长度对巷道围岩位移以及应力的影响,并结合以上参数且锚杆预紧力和间排距取定值,代入式(5),(34)和(36),得到锚杆长度与巷道围岩位移以及应力关系曲线,如图12所示。图12为锚杆长度对巷道围岩变形和应力的影响曲线,由图12可以分析得出,随着锚杆长度的增大,巷道变形明显减小,增大锚杆长度能够提高巷道围岩的稳定性。由图12可以看出,在塑性区范围内锚杆长度越大,围岩中切向应力明显提高,应力峰值随着锚杆长度减小略有升高,而且向巷道表面发生转移,在巷道周边围岩的切向应力增加。
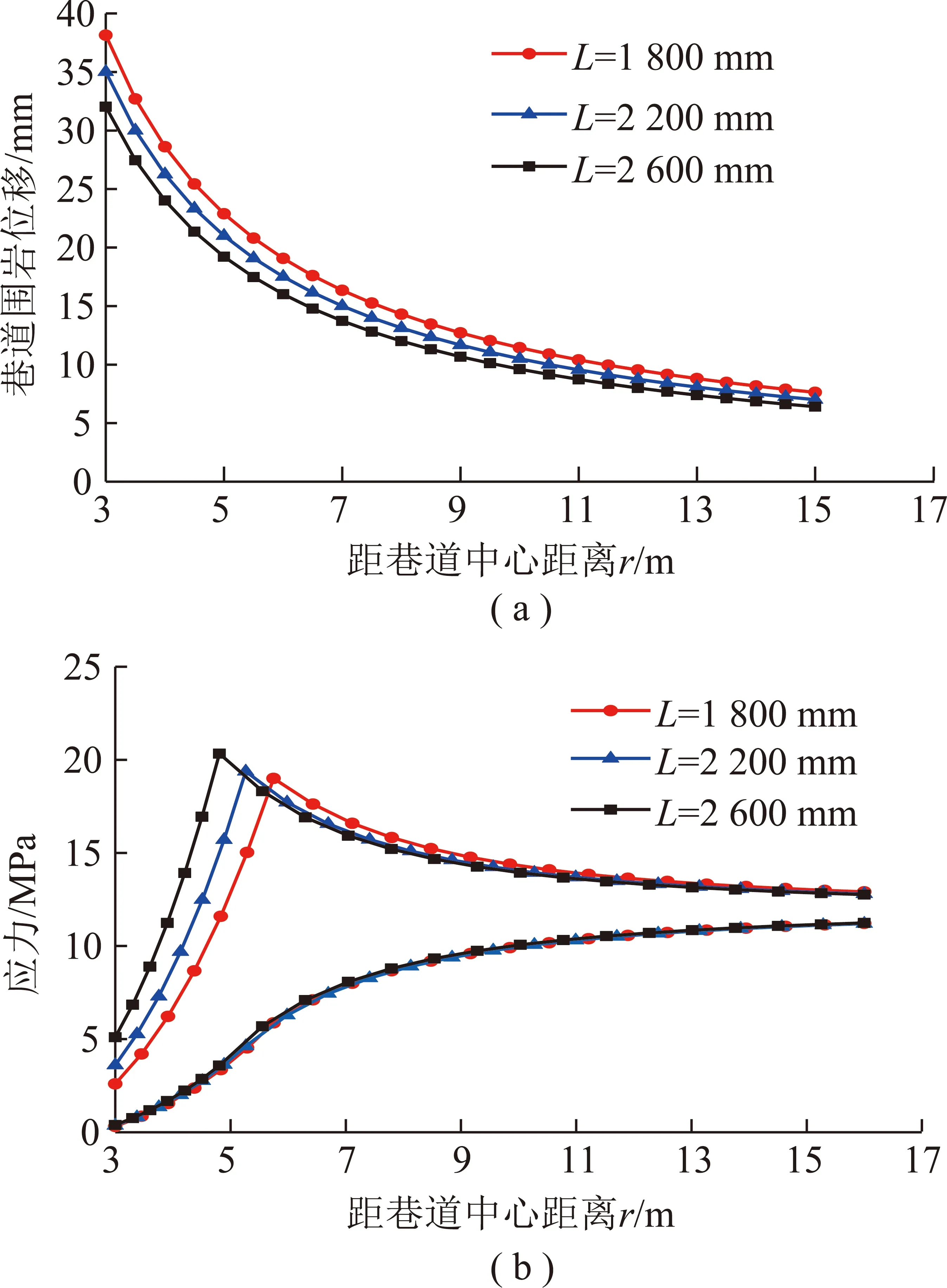
图12 锚杆长度对巷道围岩变形和应力的影响Fig.12 Influence of bolt length on surrounding rock deformation and stress of roadway
从上述分析可知,锚杆支护对巷道围岩起到了一定加固作用,对围岩进行支护后,改善了围岩的力学性能。而锚杆长度、预紧力、间排距对巷道围岩变形、围岩应力有着重要影响,合理的参数可使得围岩整体强度得以提高,抵抗变形破坏的能力明显增强。
5 巷道围岩锚固承载结构数值分析
为了研究锚固承载层对巷道围岩稳定性的影响,同时验证理论分析的合理性,本文采用FLAC3D对巷道围岩承载结构特征及支护作用进行数值模拟研究,边界条件设置上表面为自由表面,其余边界采用法向固定约束。模型尺寸沿X,Y,Z方向为50 m×30 m×50 m,其中X为巷道断面内的水平方向,Y为水平方向,Z为垂直方向,建立如图13所示的数值计算模型。根据锚杆间排距确定每个锚杆所作用的范围,如图1(d)所示。将锚杆施加的预紧力根据式(22),(32)计算每根锚杆的均布力形式下的等效支护力。在不考虑锚杆单元数值模拟计算的工况下,以相同的开挖步序模拟巷道开挖,同时在开挖面上施加锚杆等效均布力,结合锚固力学效应下形成的围岩锚固承载层范围内的参数变化,对锚固承载层结构用柱形壳体网格(cshell)建立模型,并分组,结合表1中的岩体参数进行赋参,计算至收敛即可获取当前开挖工况下的围岩力学状态。

图13 数值计算模型Fig.13 Numerical calculation model
5.1 巷道围岩塑性区数值模拟
从数值模拟的结果(图14)可知Fenner解下模拟的塑性区在5.8~6.2 m,由理论计算结果可知rp=5.98 m,可以看出数值模拟结果与理论结果基本一致。对于本文考虑锚固承载层作用下的塑形区范围,数值模拟结果的范围在4.78~4.91 m,由式(33)计算可知rp=5.08 m,与数值模拟结果相近。
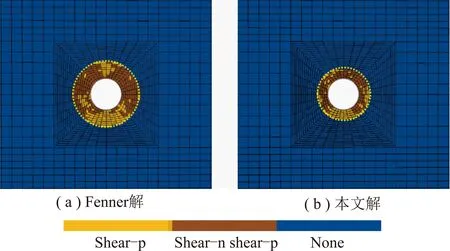
图14 塑性区分布Fig.14 Plastic partition layout
对于本文解在考虑锚固承载层作用时,塑性区范围明显减小,减小了约15.1%。锚固承载层的存在对巷道塑性区范围的发育具有明显抑制作用,巷道围岩强度增强,有利于巷道的维护。

图15 最大主应力云图Fig.15 Cloud diagram of maximum principal stress
5.2 锚固承载层应力结构分析
由图15可知巷道围岩在开挖后切向应力出现了局部集中且应力值较大。对于Fenner解下的切向应力,在巷道周围出现应力集中区域,其大小约为原岩应力的1.5倍。对于本文解下的切向应力相比Fenner解下的应力略有升高,约为原岩应力的1.67倍,且本文解比Fenner解的切向应力影响范围明显缩小,最大主应力主要出现在锚固承载层附近。锚固承载层作为围岩稳定的主要承载体,能够抑制围岩的变形,巷道表面一定范围内切向应力增大。结合理论分析可知,无论是Fenner解还是本文解都与图9中的切向应力以及最大应力出现的范围基本一致,理论分析和数值模拟的结果相近。
6 结 论
(1)基于Mohr-Coulomb准则下两线段力学模型的修正Fenner解,结合考虑锚杆预紧力下的体积力和平衡方程,求出锚固承载层的切向应力,由锚固承载层沿巷道表面垂直方向上的静力平衡方程,推导出锚固承载层内边界所能提供的等效支护力,进一步计算出锚固承载层下的塑性区半径和位移的解析解。
(2)对于锚杆支护时,在锚固承载层作用下的本文解与修正的Fenner解对比分析可知,锚固承载层的存在对巷道塑性区范围和巷道表面位移有着较好的抑制作用,对巷道围岩的稳定性更加有利,结合FLAC3D数值模拟,对理论分析的结果加以验证,得出与理论分析基本一致的结果,因此在实际锚固支护设计中应当考虑锚固承载层的存在。
(3)分析了锚杆长度、间排距、预紧力三者对等效支护力和锚固承载层厚度的影响。从文中分析可知,锚杆支护参数对改善锚固承载层力学强度起到关键作用,分析结果表明:锚杆长度越长、间排距越小,预紧力越大,能够增大等效支护力,减小巷道表面位移,巷道围岩稳定性得以提高,但锚杆长度相较于预紧力以及锚杆间排距对锚固承载层厚度影响较小。

