深井冲击载荷下液压支架底板比压分布特性

谢云跃,孟昭胜,曾庆良,杨春祥,高魁东

(1.山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地，山东 青岛 266590; 2.山东科技大学 山东省土木工程防灾减灾重点实验室，山东 青岛 266590; 3.山东科技大学 机械电子工程学院，山东 青岛 266590; 4.山东师范大学,山东 济南 250014)

液压支架是煤炭井下开采的关键支护装备，其在井下工作时不仅起到支护顶板，维护回采工作面安全作业空间的作用，同时还与工作面采运装备“互支互推”，完成开采工作面的推进工作，因此液压支架的自移性能是保障工作面安全高效生产的重要因素。尤其随着我国煤炭行业逐步向自动化、智能化方向发展，液压支架的自移性能对工作面智能化水平的制约越发明显，而影响液压支架自移性能的关键因素之一就是其底板比压分布特性[1-3]。

液压支架的底板比压分布特性是指液压支架在井下承载过程中其底座由前至后对底板形成的压力分布特性。液压支架的底板比压分布特性对其自移性能具有重要影响，若底座前端比压过大而压碎底板，则会造成支架扎底而无法移架，影响工作面开采进度，威胁作业人员安全[4-5]。随着地球浅部矿产资源的日益枯竭，未来深部资源开采必将成为常态。相对浅部煤层开采，深部开采的高围压条件更容易诱发覆岩冲击来压，而冲击压力来临瞬间，液压支架整体包括底座将承受更高的外载荷，从而导致液压支架易于形成高底板比压，降低支架的支护稳定性及自移性能。因此对冲击载荷作用下液压支架底板比压的分布特性进行研究，对指导深井开采液压支架设计优化及自移性能提升具有重要意义[6-8]。

为研究液压支架在不同工况下的底板比压分布规律，MARCIN WITEKT等[9]通过将液压支架放置于特殊的液压垫实验装置上，测试了3种不同工况下液压支架的底板比压分布状况。徐亚军基于弹性基础梁理论，对液压支架底板比压强度分布进行了理论推导，得出了底板比压变化规律近似成指数函数关系[10-11]。王志等[12]基于双参数地基梁理论建立了液压支架底座与底板互作用模型，得出了底板比压最大区域分布于柱窝下方。王恩鹏等[13]通过试验方法分析了液压支架底板比压特性，指出支架合力作用点是影响支架底板比压的重要因素。然而液压支架为大型支护装备，对其频繁开展试验成本昂贵，现有理论、数值模拟研究在讨论液压支架底板比压分布特性时，又多基于静力条件假定下讨论液压支架的底板比压分布规律(假定底板比压的分布特性曲线、底座的受载位置等)，且底座多被处理为刚性体，忽略了底座承载变形对底板比压的影响[14-16]，不符合实际工况。

基于此，笔者在前人的研究基础上，为更准确获取冲击载荷下深井开采液压支架底板比压分布特性，首先建立了液压支架的多体动力学模型，通过对支架施加不同工况的冲击载荷，获取了冲击载荷工况下液压支架各铰点载荷响应谱。随后建立了液压支架底座的柔性体分析模型，通过将获取的支架铰点载荷响应谱分别施加到底座柔性体模型对应的铰接销轴，分析了不同冲击工况下液压支架底板比压分布规律，完善了深井开采液压支架-围岩强度适应性理论。论文提出的液压支架底板比压数值分析方法，为深井开采液压支架的结构优化及自移性能提升提供新的研究思路。

1 液压支架底座铰点载荷分析

1.1 液压支架数值模型定义

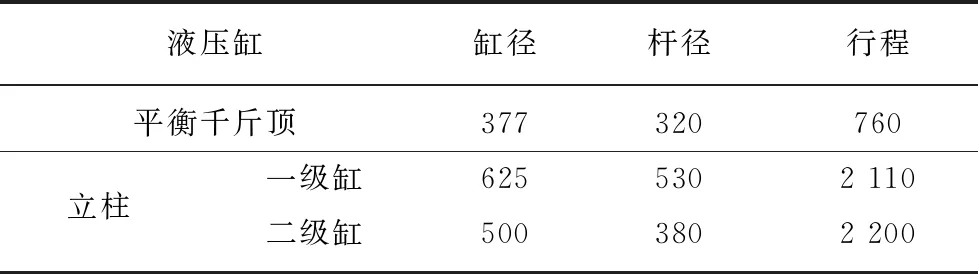
基于现有研究基础，运用多体动力学分析软件ADAMS建立液压支架的刚柔耦合分析模型[17-18]，旨在通过此模型，获取冲击载荷下底座各铰接点(立柱及前后连杆)载荷谱，为后续底板比压分析研究提供载荷依据:其中液压支架的底座与地面固定连接视为刚性体，顶梁、掩护梁、四连杆机构运用Hypermesh处理为柔性体，各构件间连接采用摩擦接触定义(摩擦因数为0.3)。立柱和平衡千斤顶采用弹簧-阻尼系统等效替换(参数见表1)，其刚度计算公式为

(1)

式中，K为等效刚度系数，N/m;A为液压缸有效传力面积，m2;β为乳化液体积弹性模量;L为液压缸有效行程，m。

表1 立柱和平衡千斤顶主要参数
Table 1 Main parameters of props and equilibrium jack

mm

依据式(1)得到平衡千斤顶、立柱一、二级缸的等效刚度系数分别为K1=206 MN/m，K2=204 MN/m，K3=100 MN/m。当立柱一、二级缸同时工作时，将立柱等效为串联弹簧，其刚度系数为K4=K2×K3/(K2+K3)=67.1 MN/m。同时为方便后续结果提取、辨别，约定了支架的左右侧，完成定义的液压支架数值模型如图1所示。

文献[12，16]指出，在对液压支架顶梁远立柱端进行单点加载时，液压支架远未到达其额定载荷时即已出现了变形失效(支架的超前失稳)，此时支架尚未形成较大底板比压。因此依据国家标准规定选取均布加载、两端加载、前方扭转、后方扭转和偏心加载5种典型工况对液压支架进行加载，以获取液压支架在额载失稳范围内承受冲击载荷时底座各铰点载荷谱，其中主动冲击载荷通过垫块施加给支架顶梁(垫块为刚性)，加载垫块布置方式如图2所示。

图2 顶梁加载方式示意Fig.2 Schematic diagram of canopy loading mode

1.2 底座铰点冲击载荷响应谱分析

对图1中的模型进行加载时考虑到支架对顶板的主动初撑作用，将模型载荷分为初撑静载和冲击动载两部分。其中初撑静载在0～3 s内缓慢增加到10 MN，随后维持2 s，以平衡液压支架所承受的初撑载荷，在5.2 s通过STEP函数将11 MN冲击力施加垫块上，以模拟支架受到的冲击动载荷，定义完成的加载曲线如图3所示。分别设置仿真计算时间为10 s，运行仿真得到不同冲击工况下底座各铰点载荷响应谱如图4，5所示。

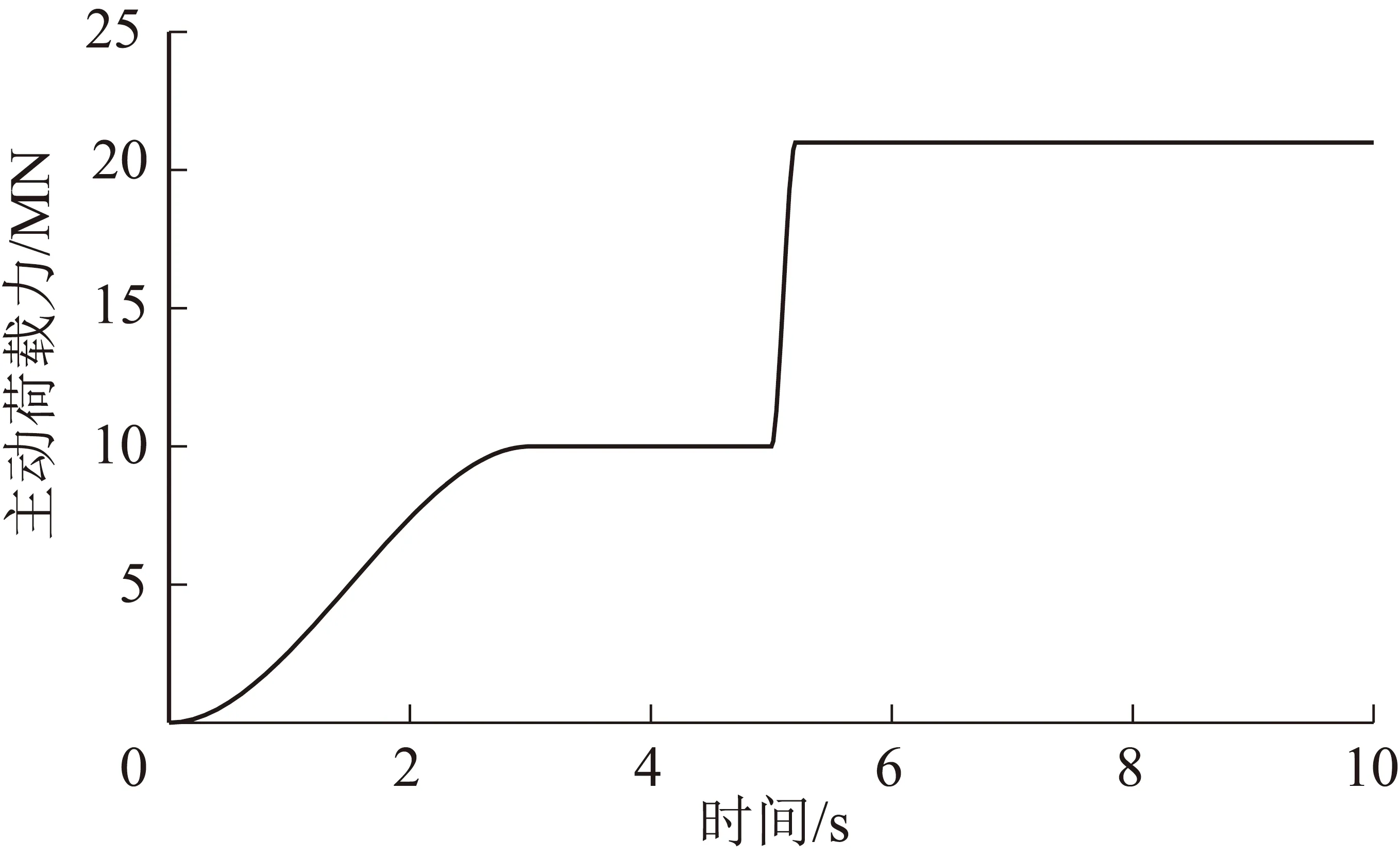
图3 主动加载曲线Fig.3 Active loading curve

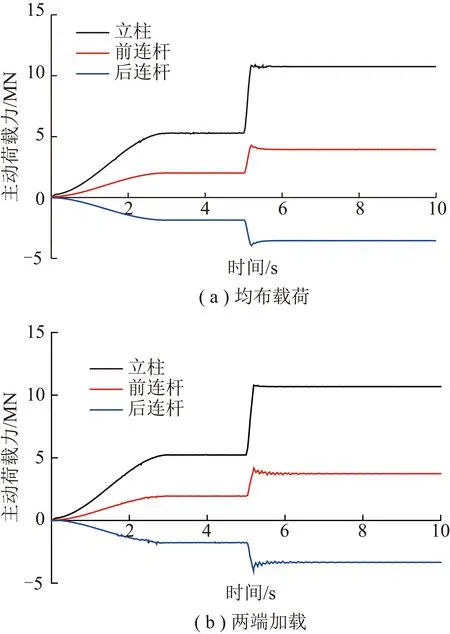
图4 对称承载工况下铰接点载荷曲线Fig.4 Load curves of hinge points under symmetric loading conditions

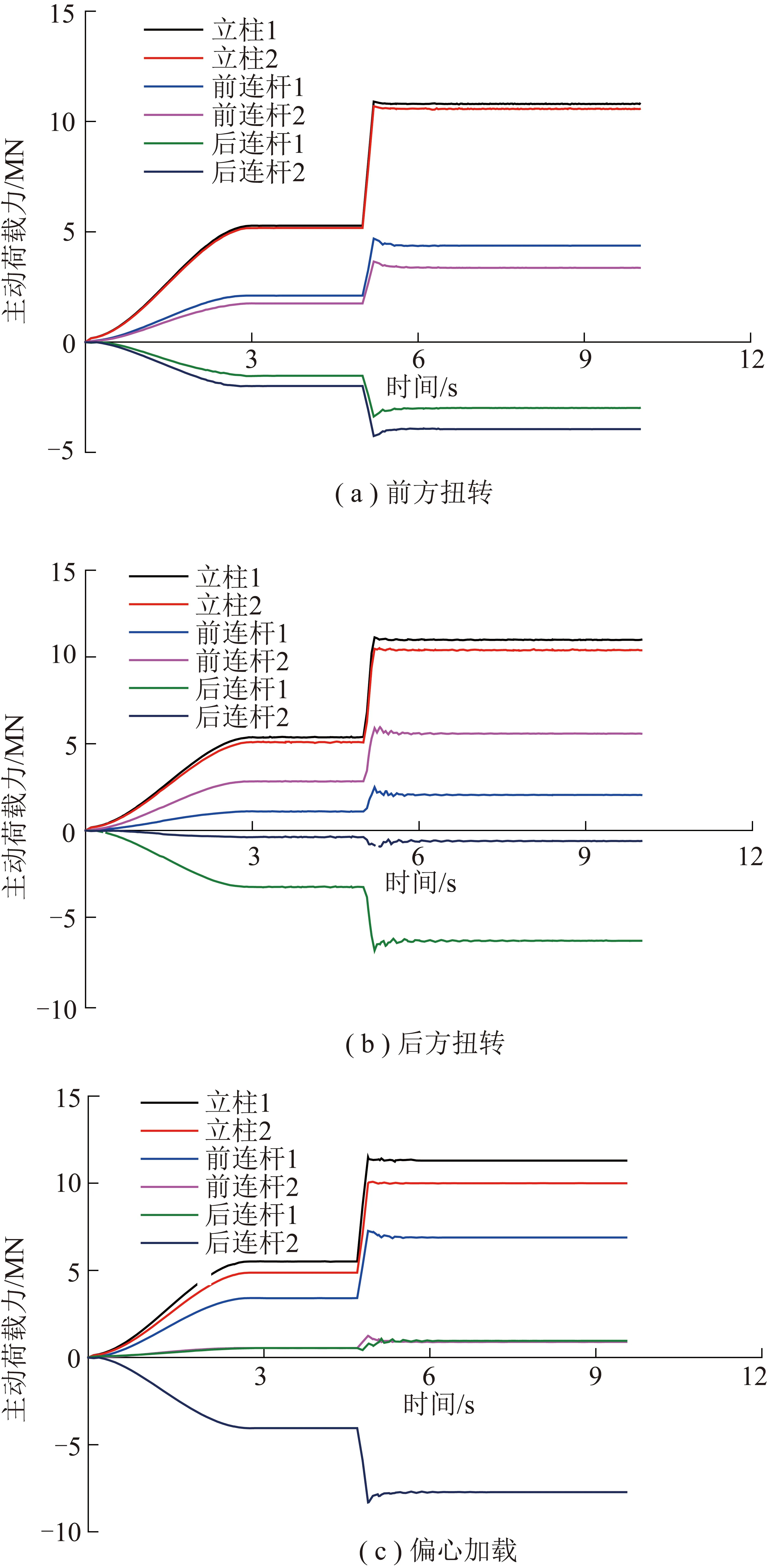
图5 非对称承载工况下铰接点载荷曲线Fig.5 Load curves of hinge points under asymmetric loading conditions

考虑对模型均布加载和两端加载时，支架所承受载荷为对称分布，立柱和前后连杆左右两侧铰接点的受力相同，所以载荷只取一侧。图5中立柱1、前连杆1及后连杆1代表支架左侧铰接点，立柱2、前连杆2和后连杆2代表支架右侧铰接点，各载荷值均取竖直向下方向为正方向。

由图4可知，液压支架在均布载荷和两端加载两种工况下，由于外载荷处于对称分布状态，支架各铰接点载荷的变化趋势基本相同:立柱铰点载荷与前连杆铰点载荷受力方向一致，且与后连杆铰接点受力始终相反;相对均布加载，两端加载工况下，各铰接点在承受冲击载荷时表现的冲击振幅更强(表2);两种工况下，立柱均为液压支架主要承载部件，在21 MN外载作用下，立柱平均承载20 MN，连杆机构平均承载3.5 MN。即液压支架顶梁承受的载荷大部分是通过立柱传递至底座上，仅有小部分载荷通过平衡千斤顶-掩护梁-四连杆系统传递至底座。

液压支架在顶梁前方扭转、后方扭转和偏心扭转3种非对称外载工况下各铰点的载荷响应谱如图5所示。由图5(a)，(b)可知，在前方扭转与后方扭转加载工况下，液压支架前后连杆与底座铰接点受力方向始终相反(各铰点载荷方向与对称加载时各铰点载荷方向保持一致)，且因外载的偏载效应，支架左右两侧铰接点承受的载荷相差极大，后方扭转工况时这一偏载效应尤为剧烈:相较于前方扭转工况，在后方扭转工况下两颗立柱的载荷差由0.2 MN上升到0.6 MN，前连杆载荷差由1 MN上升到3.5 MN，后连杆载荷差更是由0.96 MN上升到5.7 MN(偏载系数均>3)。在偏心加载工况下(图5(c))，由于液压支架只承受单侧偏载力(无对称平衡力)，此时两侧连杆铰点力载荷差进一步扩大，后连杆两侧铰接点受力方向甚至出现反向工况，载荷差达到6.87 MN。表2为支架在冲击载荷出现后各铰点力响应峰值与稳定值的比值关系。相对立柱，前后连杆振动更剧烈，且在后方扭转与偏载工况下，前后连杆振动幅值最高。

2 液压支架底板比压分析

2.1 底板比压分析模型

考虑液压支架实际工作时，来自前序构件的载荷(自顶而下，顶部相对底部为前序)均通过销轴传递至下一构件，因此在建立液压支架底板比压分析模型时，建立包含销轴的底板比压分析模型以模拟液压支架底座的真实载荷传递工况。同时考虑支架底座铰接耳座结构均为箱型结构，销轴与底座的接触方式并非整体接触而是呈环形分布，建立环形加载面SEGMENT进行载荷传递，此外加载面可实现对连杆力载荷角度的模拟，最终建立如图6所示的液压支架底板比压分析模型。其中底座和销轴材料定义为钢:泊松比为0.3，质量密度为7 850 kg/m3，弹性模量为210 GPa，底座与销轴、底板之间采用面-面摩擦接触，摩擦因数设置0.3。底板四周及底部采用固定约束，底板选用砂岩(Mohr-Coulomb模型):质量密度为2 670 kg/m3，剪切模量为2 580 MPa，泊松比为0.17，内摩擦角29°，剪胀角14°，黏聚力3.5 MPa。

表2 各铰接点冲击载荷响应峰值与稳定值的关系
Table 2 Relationship between peak value and stable valueof impact load response of each hinge point

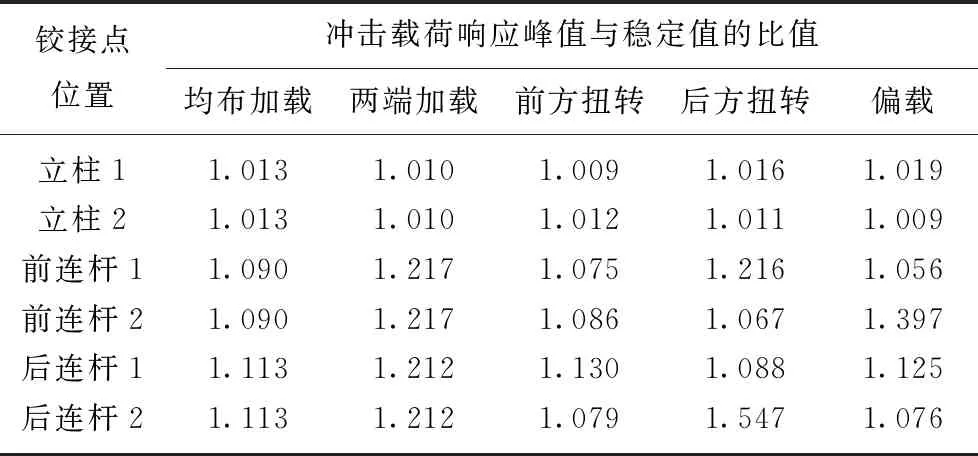
铰接点位置冲击载荷响应峰值与稳定值的比值均布加载两端加载前方扭转后方扭转偏载立柱11.0131.0101.0091.0161.019立柱21.0131.0101.0121.0111.009前连杆11.0901.2171.0751.2161.056前连杆21.0901.2171.0861.0671.397后连杆11.1131.2121.1301.0881.125后连杆21.1131.2121.0791.5471.076

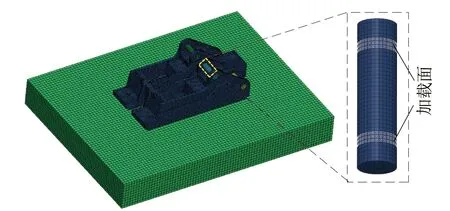
图6 基于LS-DYNA建立的底板比压分析模型Fig.6 Floor specific pressure analysis model in LS-DYNA

2.2 结果及分析

液压支架在承受冲击载荷时，由于外载荷在极短时间内迅速增加，而支架本体尤其是依靠内部封闭乳化液传递动力载荷立柱和平衡千斤顶部分响应速度缓慢，且由于安全阀的泄压滞时效应，立柱及平衡千斤顶内部压力无法及时排出，从而导致立柱及平衡千斤顶刚度剧增(形成类刚体结构)，促使顶板冲击载荷瞬间峰值直接传递至底座，使得底座受力突增、底板比压增大，威胁液压支架的正常使用。在采用LS-DYNA对底板与底座耦合模型进行仿真求解时，为更为详尽地获取液压支架底板比压分布特征，以底座左前端为原点，定义底座长度方向为X方向，宽度方向为Y方向，建立如图7所示的坐标系，并提取图中6条直线所示位置的底板上网格单元的比压值绘制底板比压分布曲面。

图7 底板比压分析结果提取位置示意Fig.7 Extraction position of floor specific pressure analysis results

图8(a)为液压支架承受顶梁均布冲击载荷时的底板比压分布图，此时顶梁上方承受均布载荷，但底座后方仍存在明显的无压区(比压为0的区域)，即此时底座后端已出现翘曲变形，脱离底板。定义图中黑色曲线为“底座与底板分离线”(以下简称分离线)，则分离线后方为无压区，这一现象与波兰学者Marcin Witekt实验结果基本吻合，不同的是Marcin Witekt采用刚性接触实验方式测试支架的底板比压，因此底座前端比压呈近线性分布。而实际上虽然液压支架底座刚度相对底板极大，但由1.2节分析可知，来自顶板的载荷主要由立柱传递至底座(图8(a)中底板所受载荷主要集中在底座柱窝下方区域，柱窝下方比压达到7.5 MPa)，因此底座柱窝处相对底座前端、后端会产生更大变形，反映到底座与底板的耦合模型中时，会表现出如图8(a)所示的底座柱窝处压入底板最深(底座前端比压相对柱窝处较小，约为0.5 MPa)，即此时液压支架整体呈现出前端沉陷-中部压入-后端翘曲的“V型”姿态。同时，由于此时外载荷沿Y方向成对称分布，因此图8(a)中底板比压基本呈左右对称分布，且分离线呈平行于Y轴的直线状。

均布加载工况下液压支架底座应力云图如图9(a)所示。由图9(a)可知，底座在受冲击后发生弯曲变形，其中最大挤压应力主要分布在前连杆与底座铰接点内侧的弧形过渡处以及柱窝处底座内侧筋板，最大应力约为345 MPa。观察底座与底板下接触面，不难发现在均布载荷作用下，底座对底板压力分布较均匀。同时由于柱窝处采用了π型卸压筋板结构，在柱窝正下方处底座未表现出明显的应力集中峰，而是在卸压筋板处形成了分段的小压力峰，大大减小了柱窝处的应力、应变集中水平。

两端加载工况下液压支架底板比压和底座应力分布分别如图8(b)，9(b)所示。由图8(b)，9(b)可知，常相似:底板比压最大处依然为底座两脚的柱窝下方，约为7.4 MPa，略小于均布加载工况;支架底座整体比压基本对称分布，其中底座前端比压仍为0.5 MPa，分离线为平行于Y轴的一条直线。不同的是，由于两端加载时立柱后端载荷比加大(立柱位于顶梁后半段)，进而导致底座前倾量相对减小，因此分离线向后移动至2.2 m处。此时对应底座筋板处应力最大值也由均布加载时的345 MPa减小至304 MPa。从底座比压分布角度出发，由于顶板集中载荷的后移，两端集中承载工况相较于均布承载工况，底座后端将承受更多外载荷，底板稳定性更易控制。

顶梁前方扭转加载工况下液压支架底板比压分布如图8(c)所示。与均布载荷和两端集中加载相比，最明显的差异为此时底板比压不再呈对称分布。虽然前方在扭转工况下，底板比压最大位置依然位于柱窝下方，但因前后加载力制约，柱窝处的最大比压约为7.1 MPa，小于均布载荷(7.5 MPa)和两端加载(7.4 MPa)。从前端比压强度看，加载侧前端底座比压可达0.6 MPa，略高于前述两种对称加载工况(0.5MPa)。同时由于顶梁右前端无载荷平衡后端载荷，此时分离线右端向前方出现了明显的前移，且底座左前侧(加压侧)底板比压明显大于右侧。

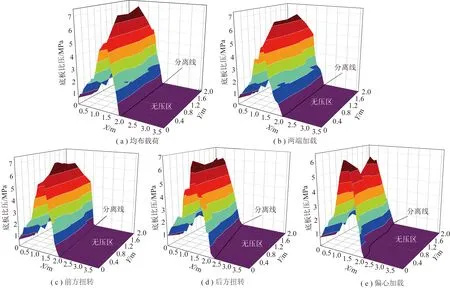
图8 均布载荷工况下底板比压分布Fig.8 Distribution of the floor specific pressure under normal loading conditions

顶梁前方扭转加载工况下液压支架底座应力云图如图9(c)所示。由图9(c)可知，此时底座最大应力仍然分布在前连杆与底座铰接点内侧的弧形过渡处以及柱窝处底座内侧筋板处(最大应力约320 MPa)，大于两端加载工况。同时观察底座下表面应力分布，不难发现加压侧(右脚)应力明显大于自由侧(左脚)。

图8(d)，9(d)为后方扭转工况下底板比压分布图和底座应力云图。由图8(d)，9(d)可知，在顶梁后方扭转工况下，液压支架底板和底座的应力变化相较前3种工况进一步增大，底座最大应力值位置出现在加载侧柱窝的内侧(约658 MPa)。由于顶梁柱窝后方载荷的明显降低，柱窝处底座比压已降至6.85 MPa，而前端比压增加至0.9 MPa，此时分离线基本呈一条倾斜的直线。

观察底座下表面应力分布可知，底座左脚各点应力差距不大，而右脚各点应力却有明显差异且应力明显大于左脚，结合1.2节分析不难发现，由于前后连杆铰接点的力差(前连杆铰点左侧受力较大，后连杆铰点右侧受力较大)，导致底座发生了明显的扭转变形，严重影响了底板比压和底座应力的分布。从数值上看，后方扭转工况下底板比压和底座应力最大值均大于前方扭转，特别是底座应力最大值已达前方扭转工况的2倍(658/320≈2.1)，说明后方扭转工况下支架-底板破坏失稳概率明显大于前方扭转工况。

偏心加载工况下液压支架底板比压及底座应力分布情况如图8(e)，9(e)所示。由图8(e)，9(e)可知，在偏载分布工况下，由于顶梁右侧无外载荷，此时分离线已明显转化为1条“台阶”曲线。此时底座比压值横向波动较大，比压峰值出现在偏载侧柱窝下方(比压峰值6.27 MPa，为5种工况下最小)，而底座最前端下方比压约为0.6 MPa。观察底座下方应力云图，不难发现偏心加载时支架左脚受力主要影响区域为柱窝所在位置，而右脚两侧主筋板及底面都受到影响。底座应力最大值为553 MPa，介于后方扭转及前方扭转工况之间。

分别提取5种工况下液压支架加载侧底座下方(图7中曲线2位置)单元应力峰值与稳定值如图10所示，5种不同加载工况下冲击载荷均引起底板比压产生不同程度的升高，且底板比压响应峰值普遍高于稳态响应值。但总体而言，冲击载荷的出现并未改变底板比压的分布特征:5种不同冲击载荷作用下，支架底板比压均表现出明显的非线性分布，而是呈前端沉陷-后端翘曲姿态(底板破碎前)的“V”型分布，即不同加载工况下底板比压危险区均出现在底座前半部分。因此深井开采液压支架更应注重其底座结构的设计、优化，以降低支架前端比压分布，提升支架的支护稳定性及自移性能。

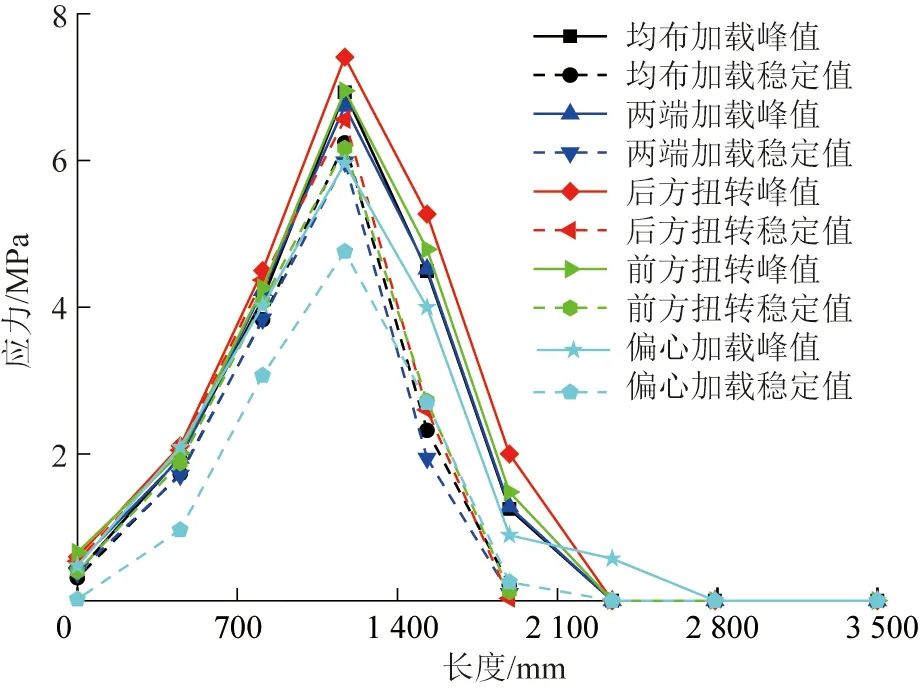
图10 冲击载荷对底板比压的影响Fig.10 Influence of the impact load on the floor specific pressure

3 结 论

(1)冲击载荷来临时，支架各铰接点力响应表现出不同的敏感性，前、后连杆相对立柱振动更剧烈，由于立柱是支架的主要传力承载结构，因此冲击载荷作用前后并未改变支架底板比压的总体分布特征，而主要影响了底板比压峰值。所以深井开采时，频繁、高强度的顶板冲击载荷会恶化液压支架与底板的耦合状态，降低液压支架的稳定性与自移性能。

(2)液压底板比压并非呈简单的线性分布，而是沿底座长度整体呈现出从前至后先增大后减小的“V”型分布规律。虽然支架在深井开采时承受的外载荷多种多样，但底板比压危险区域均出现在底座前半部分。因此深井开采液压支架更应注重其底座结构的设计、优化，以降低支架前端比压分布，提升支架的支护稳定性及自移性能。

(3)不同冲击载荷工况对支架受力和底板比压的影响各不相同，总体而言当冲击外载变化时，支架自身应力变化比底板比压变化更加敏感。在对称冲击载荷作用下，支架应力及底板比压均呈对称分布且变化较小。在非对称冲击载荷作用下，支架应力及底板比压均变化较大，其中后方扭转加载工况下支架前端底板比压达最大值(0.9 MPa)。