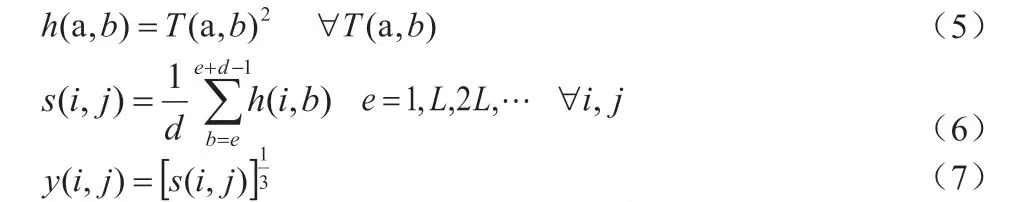基于耳蜗倒谱系数的说话人识别

曾金芳 徐文涛 黄费贞

（湘潭大学物理与光电工程学院 湖南省湘潭市 411105）

说话人识别又叫声纹识别。说话人识别技术以其独特的方便性、经济性、准确性受到 了世人的瞩目，被广泛应用到信息安全领域、通信领域、司法领域和军事领域[1]。说话人识别就是从说话人的一段语音中提取出说话人的个性特征，通过对这些个性特征的分析和识别，从而达到对说话人进行辨认的目的[2]。这些个性特征就是说话人识别重点研究的内容。

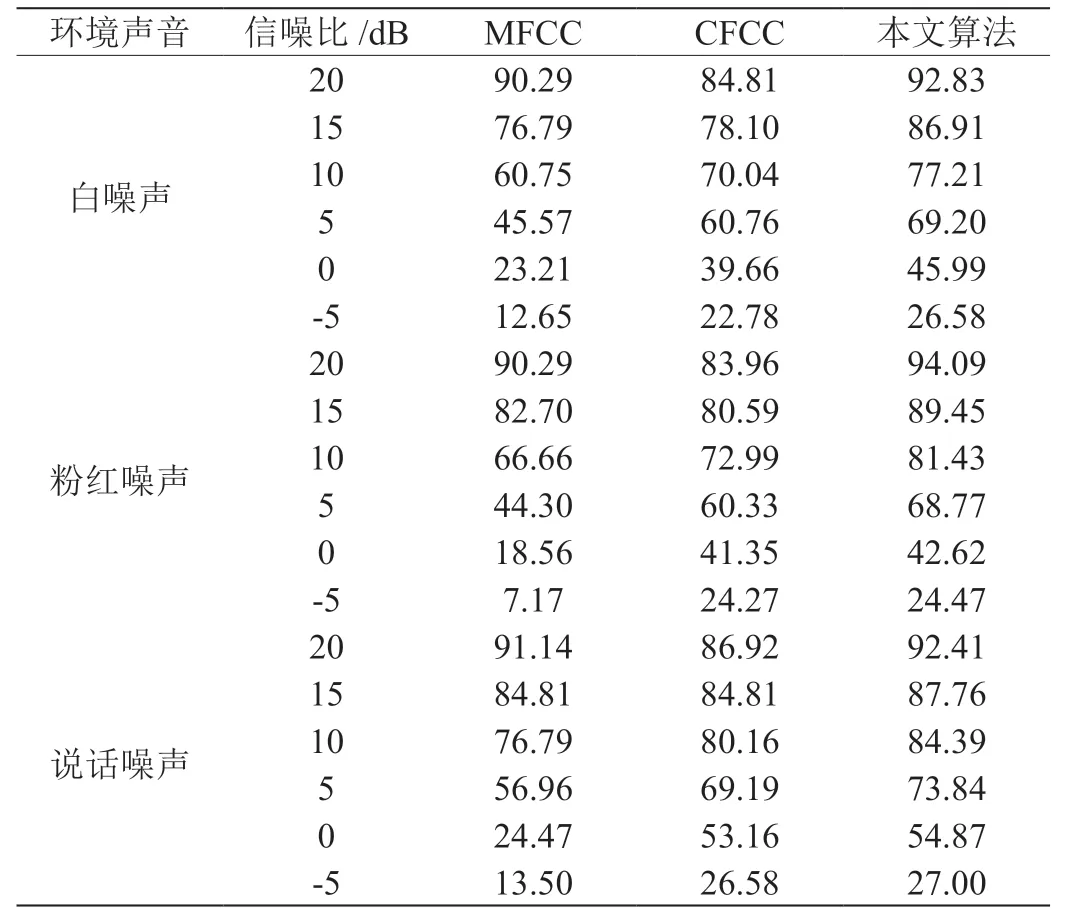
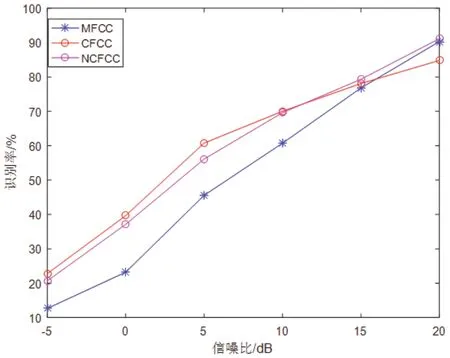
声学特征主要有:线性预测系数(Lin- ear prediction cepstral coefficient, LPC C)、梅尔倒谱系数( Mel frequency cepstral coefficient, MFCC)[3]以及耳蜗倒谱系数(Cochlear filter cepstral coeffi- cients, CFCC)[4]等。最常用的MFCC 是根据人耳结构设计的三角滤波器组进行特征提取的，但在噪声情况下的识别效果急剧下降[5]。CFCC特征提取方法并没有考虑到人耳听觉的神经元动作电位发放率与声音强度的饱和关系特性，而这种关系特性推导出非线性幂函数可以近似于听觉神经元[6]。通过对文献[6]的算法实验分析，发现其非线性幂函数参数调整为1/15 时，在说话人识别方面信噪比较高的情况下有较好的效果。为了提高低信噪比情况下说话人的识别率，本文将语音增强算法的维纳滤波[7]加入前端处理。虽然增加了步骤，但总体上容易实现。

笔者在前人研究的基础上，在说话人识别方面采用能够模拟人耳听觉特性的非线性幂函数提取新的耳蜗倒谱系(New Cochlear filter cepstral coeffici- ents,NCFCC)，验证NCFCC 特征对于CFCC的优势和缺点，然后通过维纳滤波来改进其缺点。

1 CFCC特征参数提取

CFCC 是由贝尔实验室的Li Q 在2011年首次提出的并应用于说话人识别的特征参数[4]。CFCC 特征参数提取方法如图1 所示。

假设f(t)是一个原始的输入语音信号，则耳蜗滤波器变换的函数可以定义为：

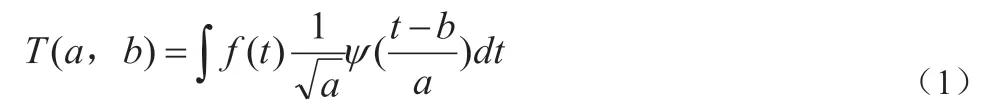
式中：a,b 为实数。

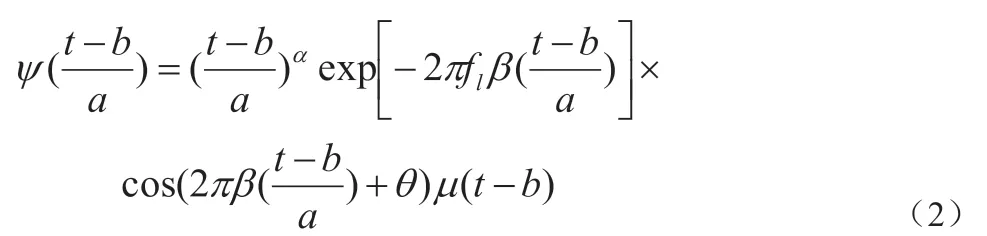
式中：α>0 和β>0，α,β 决定了ψ(t)的频域形状和宽度，α 和β的一般取经验值为α=3、β=0.2。θ 为控制冲激响应的角度，它的取值应该满足积分表达式：

μ(t)为单位步进函数，b 为随时间可变的实数，a 为尺度变量，一般情况下可由滤波器的质心频率fc和最低中心频率fL决定：

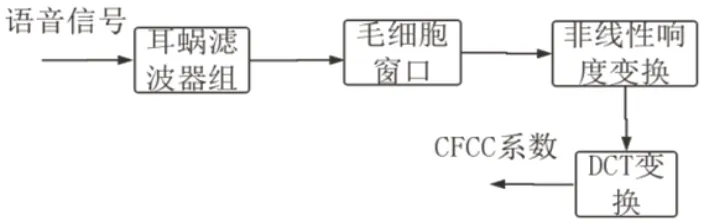
图1：CFCC 特征提取框图

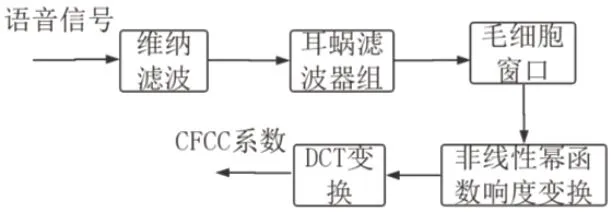
图2：本文特征提取过程

由式（4）可知，a 的取值范围0

式中：d=max{3.5τi, 20ms}, τi表示第i 个子带中心频率的周期，j 为帧数；L 为分帧的帧移。对y(i,j)进行离散余弦变换(DCT)变换从而提取CFCC 特征。

2 非线性幂函数和维纳滤波的特征提取

2.1 非线性幂函数的特征提取

CFCC 作为听觉特征参数，式（7）的提取过程中采用立方根函数来模拟非线性响度变换的过程。虽然立方根可以得到很好的模拟效果，但听觉特性的非线性不一定就是立方根，可以是非线性幂函数或对数函数等。经过试验在高信噪比的环境下立方根的效果不是很理想，而非线性幂函数却有比较好的效果。通过实验非线性幂函数比对数函数和立方根有更好的效果，因此采用NCFCC 来模拟人耳听觉特性。多次实验发现非线性幂函数取1/15 效果最好，其方程可表示为：

2.2 维纳滤波

表1：纯净语音下算法识别率对比

表2：三种噪声情况下算法识别率对比

图3：白噪声环境下识别结果对比

维纳滤波的基本原理是根据全部过去的和当前的观察数据来估计信号的当前值，它的解是以均方误差最小为条件所得到的系统的传递函数Н(w)形式给出的。

设带噪语音信号为：

其中，x(n)表示带噪信号；s(n)表示纯净语音；v(n)表示噪声。则经过维纳滤波器h(n)的输出响应y(n)为：

理论上，y(n)应尽量接近于s(n)，因此y(n)为s(n)的估计值。h(n)的频域为Н(w)：

其中，Ps(w)为x(n)的功率谱密度；Pv(w)为噪声的功率谱密度。本文算法提取过程如图2。

3 实验设计与分析

试验环境是在MATLAB R2016a 平台下完成的。试验过程通过TIMIT 语音库说话人79 人（56 男，23 女）进行试验，每个说话人录制10 段语句，7 段用于模型训练，3 段用于测试。分类器采用高斯混合模型。

3.1 试验一

为了验证NCFCC 算法的有效性及其在噪声环境下的识别性能，分别用NCFCC 算法和CFCC 算法以及MFCC 算法进行比较，噪声采用Noisex- 92 噪声数据库中的白噪声进行噪声环境的仿真实验。纯净环境下实验结果如表1，加噪环境下实验结果如图3。

对表1 和图3 的实验分析，得出NCFCC 算法在高信噪比情况下比CFCC 的识别率好，但低信噪比的情况下识别率略差。而经典算法MFCC 虽然在纯净语音情况下识别率较高，但其鲁棒性相对于CFCC 和NCFCC 来说较差。

3.2 实验二

由于低信噪比情况下NCFCC 算法比CFCC 算法的识别率略低，因此在前端加入维纳滤波器，以提高语音信号的信噪比，从而得到本文算法。本文算法和CFCC 算法以及MFCC 算法在三种噪声情况下对比。实验结果如表2。

通过表2 可以发现本文算法相对于CFCC 算法识别率基本都有明显提高。

4 结语

本文通过改进CFCC 的非线性幂函数，然后在其前端加入维纳滤波器的方法整体上提高了说话人识别率。从上面实验可以发现改进的算法在信噪比高的情况下识别率有所提高，就可以通过语音增强的方式来提高整体的说话人识别率，从而整体上提高算法的抗噪性能。