三角形中一类多元最值问题的处理策略

王国军

(河北省石家庄市第二中学，050000)

解三角形问题既是三角函数和平面向量等数学知识的延伸与应用,也是高考数学中的必考题,综合考查学生利用运用正弦定理、余弦定理、勾股定理和射影定理及面积公式解决问题的能力.三角形既有边与角两类相关元素,又有丰富的图形内涵,一类以解三角形为背景的多元最值问题成为命题的亮点.下面对这类问题进行解读,给出思考的方向和可操作的步骤,供大家备考参考.

一、求两边和的取值范围或最值

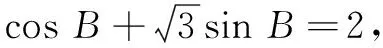
分析化简已知条件,明确a、c间的具体关系,再利用三角形中的相关定理，将其化为函数问题.

评注已知三角形的一条边及其对角,求另两边和的取值范围问题的解决策略是利用正弦定理将边元结构转化为角元函数,再利用三角函数的性质求得目标结构的取值范围.

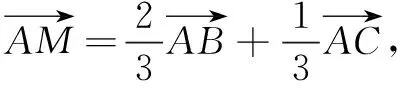
二、求两边平方和的取值范围或最值

(1)求角C的大小;

(2)当c=1时,求a2+b2的取值范围.

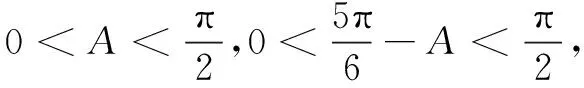
评注对于已知三角形的一条边及其对角,求另两边平方和的取值范围问题，类型一的解决策略仍然有效.将边元结构统一转化为角元函数,是求边元和结构取值范围的重要途径.

三、已知边元和结构存在最值,求参数的取值范围问题

分析将多元结构最值的存在性问题转化为函数最值的存在性问题.

思路1利用正弦定理处理b、c的关系

解法1(利用辅助角公式)

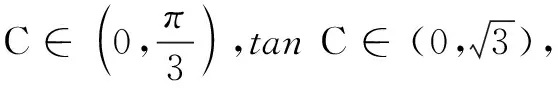
解法2(利用柯西不等式)

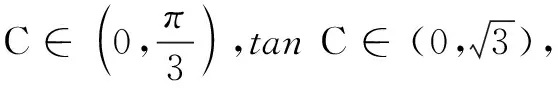
解法3(利用导数)

以下同解法1.

思路2利用余弦定理处理b、c的关系

以下同思路1求解,具体过程从略.

评注对于已知一组边及对角,求其余两边和的取值范围问题,处理的方向是转化为函数的值域问题,处理的关键是消元,最终将问题转化为角元的函数值域问题.

四、边元结构恒成立条件下,求参数的最值

评注本题采用了整体代换的思想, 将齐次边元结构统一转化为角元形式, 再利用求最大值的常规方法求得最大值. 读者可尝试一下，利用辅助角公式或者导数的方法求得函数f(A)的最大值,此处从略.

高中数学的学科教学目标不能只是单一地传授知识,而是要培养学生的数学核心素养.在数学教学过程中,不能就题解题,必须揭示数学思维活动的具体过程,把老师思考活动的过程完全展示给学生,可以使学生更好地认识、理解数学,培养和提高学生的数学能力和理性精神.