用MATLAB进行棒材生产线车间分段剪至冷床距离的优化计算

周立骞

（中冶京诚工程技术有限公司，北京 100176）

影响棒材连轧车间总长度的主要因素之一是分段剪到冷床入口的距离。轧件经分段剪切成倍尺后，先加速，与后一根轧件脱离，然后匀速运动一段距离，最后制动停止，进入冷床（图1）[1]。生产实践证明：如果分段剪与冷床入口距离过短，则前后倍尺钢无法拉开足够的距离，导致轧件进入冷床容易产生乱钢情况，耽误正常生产；过长，则会使车间长度增加、厂房面积增大，导致投资相应增加。因此，为了保证棒材生产的正常进行，减少投资费用，需要科学合理的计算这一距离。

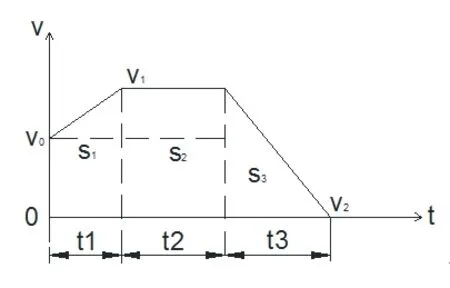
图1 轧件速度变化示意图

1 优化条件

（1）某棒材车间生产线最大终轧速度v0=18m/s，加速后最大速度v1（1.05v0～1.10v0），上冷床前速度v2=0m/s，制动裙板最短运动周期2.2s。

（2）制动开始时前后轧件头尾拉开的距离L=1m。

（3）辊道对钢的摩擦系数f1=0.3，制动裙板对钢的摩擦系数和过渡板对钢的摩擦系数f2=0.35。

（4）辊道与水平面的夹角α=12°，制动裙板斜面与水平面的夹角β=35°。

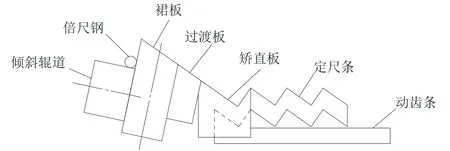
图2 上冷床装置结构

（5）轧件上冷床的过程[2]。

①轧件经倍尺剪切之后，在辊道上加速，与第2根倍尺钢脱离，进入冷床入口辊道（倾斜辊道），此时裙板在高位；②当裙板下降到低位时，第1根倍尺钢滑下，落到裙板顶面与过渡板侧面形成的夹角处，开始摩擦制动；③裙板立刻返回到中位，使第2根倍尺钢仍沿倾斜辊道运行，第1根倍尺钢完成摩擦制动；④裙板上升到高位，第1根倍尺钢滑落到冷床矫直板第1个齿槽中，然后在向冷床出口一步一步输送的过程中空气自然冷却；⑤裙板下降到低位，第2根倍尺钢滑下，开始下一工作周期。

2 建立模型[2]

2.1 加速段加速度a1的确定

钢材在加速辊道上的状态及受力情况。

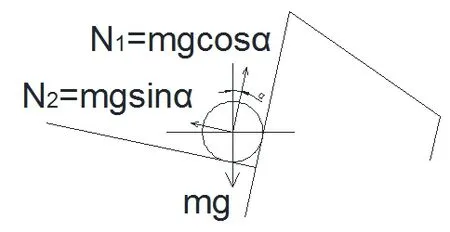
图3 钢材在加速辊道上的状态及受力情况

由图可得：

N2cosα=N1sinα

N2sinα+N1cosα=mg

解此联立方程组，得：

N1=mgcosα

N2=mgsinα

式中：N1—辊道对轧件的支持力；

N2—裙板对轧件的支持力；

m—轧件质量；

g—重力加速度，取10m/s²。

由摩擦定律及牛顿第二定律可得

ma1=N1f1-N2f2=mgf1cosα-mgf2sinα

a1=g(f1cosα-f2sinα)

2.2 减速制动段加速度a2的确定

钢材在减速段即在制动裙板上的状态及受力情况。

图4 钢材在制动裙板上的状态及受力情况

由图可得：

N3sinβ=N4cosα

N3cosβ+N4sinα=mg

解此联立方程组，得：

N3=mg[cosα/cos（β-α）]

N4=mg[sinβ/cos（β-α）]

由摩擦定律及牛顿第二定律可得：

ma2=f2（N3+N4）=mgf2[（cosα+sinβ）/cos（β-α）]

a2=gf2[（cosα+sinβ）/cos（β-α）]

2.3 距离优化

设S为轧件加速、匀速到最后制动所走过的总路程，S1，S2，S3分别为加速、匀速、制动阶段轧件所走过的路程，则：

S=S1+S2+S3

S1=v0t1+a1t12/2

S2=v1t2=（v0+a1t1）t2

S3=v1t3-a2t3

2/2=（v0+a1t1）t3-a2t3

2/2

根据工艺要求.前后两轧件在制动开始时，头尾应拉开距离L(m)，可得关系式：

L=S1+S2-v0（t1+t2）

L=v0t1+a1t12/2+（v0+a1t1）t2-v0（t1+t2）

则t2=（2L-a1t12）/2a1t1

因v1=a2t3，所以t3=v1/a2=（v0+a1t1）/a2

将t2、t3代入S并整理，得：

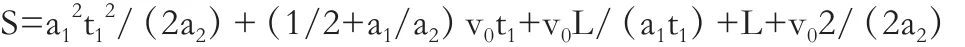
t=t1+t2+t3≥2.2

将t2、t3代入t并整理，得：

-a1（a1/a2+0.5）t12-a1（v0/a2-2.2）t1-L≤0

将数值代入计算，得：

a1=2.21m/s2，a2=5.90m/s2

建立模型（用x替换t1）：

minS=0.414x2+15.742x+8.145/x+28.458

s.t. -1.93375x2-1.88071x-1≤0

x≥0

3 MATLAB计算

（1）m文件：非线性不等式约束（图5）。

（2）非线性目标函数运算（图6）。

（3）运算结果：t1=0.706s；S=51.315m。

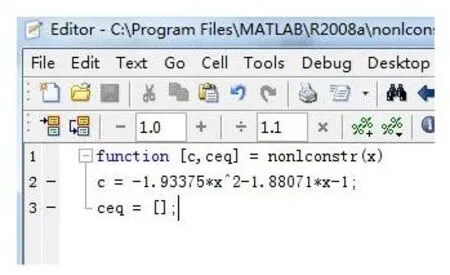
图5 将目标函数模型设置为非线性不等式约束

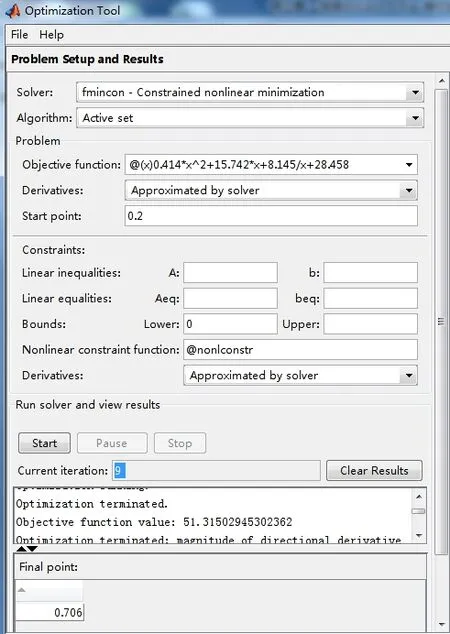
图6 目标函数计算

4 结果分析

优化后的距离为51.315m，此距离是在最高轧制速度18m/s的条件下得出，因此满足各种规格棒材的生产。

加速段时间为0.706s，加速后的速度v1=19.56m/s，比初速提高8.7%。按照生产经验，加速后，速度需提升5%～10%。本次优化计算得到了最优加速量，从而计算出最优距离。不会因距离过短，在进入冷床时产生乱钢；也不会因距离过长而增加占地和投资。