考虑不规则驾驶行为的城市隧道事故率预测
杜 蕊, 蔡晓禹, 谭 静
(1.重庆交通大学交通运输学院, 重庆 400074; 2.重庆交通大学山地城市交通系统与安全重庆市重点实验室,重庆 400074)
随着城市的快速发展,城市交通行业也在急速发展,然而全球每年的交通事故造成125×104人死亡,交通事故的伤害位列全球第八致死原因,交通安全相关研究迫切需要。据相关统计,2018年上半年仅青岛胶州湾隧道就发生事故近300起。传统的交通安全管理方法已经无法满足智慧隧道运营管控需求。面向信息化、大数据的智慧隧道交通环境,主动交通安全管控对于有效预防交通事故发生,缓解事故引起偶发性拥堵,提升城市隧道交通运行效率至关重要。探索隧道交通事故的发生机理,判别事故发生的潜在可能性是主动交通安全管控所面临的关键挑战。
事故率预测主要针对于事故发生前紊乱的交通流现象进行对比分析研究,采用统计模型研究事故发生与交通流状态的关联性分析,以利用事故发生前的主要交通特征数据建模,实现交通事故风险的预测。近几年,中外很多学者对道路交通事故预测进行了研究,常用于交通事故预测的模型有回归模型法、神经网络法以及贝叶斯网络等。Cheng等[1]基于观测数据对三个道路事故频率预测方法进行评估,并提出经验贝叶斯法较于时间序列法和简单置信区间法对事故频率的预测精确度更高的结论。陈海龙等[2]基于对BP神经网络模型的改进,对影响交通事故严重程度的多种影响因素进行分析,以预测事故的严重程度,得出道路摩擦系数、光照以及天气与事故严重程度关联较大的结论。段萌萌等[3]引入“桥隧比”参数研究了高速公路事故发生的影响因素,提出基于多元回归的事故预测模型。
在交通事故预测研究方面,中外较多研究事故与道路影响因素以及天气之间的关系,例如道路摩擦系数、道路线性、道路组成、雨天、大风天气等,分析不同影响因素之间事故发生的严重程度以及事故率变化等[4-7]。或者仅针对高速公路上事故黑点进行研究与识别[7-9],通过收集事故资料,并统计分析事故在道路上的分布规律,构建交通事故灰色区域识别预测模型[10-11]。而在微观层面上,对于城市道路隧道内交通事故率预测研究相对较少,且大多从间接因素角度分析、研究交通事故的发生原因[13]。
基于2018年5月、6月青岛胶州湾隧道的交通事件数据,结合交通运行、车辆行为等样本数据,将所有事件随机的分为训练集和验证集。基于训练集数据采用条件Logistic概率函数方法对事故发生概率进行建模,分析事故发生的显著性影响因素,最后利用验证集数据对模型的预测精度进行检验评价。
1 Logistic理论原理
1.1 Logistic模型
为了探讨交通运行参数与道路事故发生的可能性之间的机理关系。本研究选取比利时数学家Pjerre-Francois Verhulst提出的Logistic概率函数[14]。
(1)
式(1)中:N(t)为t时刻某研究对象的数量;k为在一定环境下的研究对象的最大极限值;r为研究对象的增长率。
此后,英国统计学家David Cox对Logistic函数进行了改进[15]。使得Logistic模型可以基于单个或多个预测变量参数得到二分类变量的对应概率值,同样可以定量分析各因素变量对于二分类变量的影响关系。即设一个二分类因变量,因变量的值只能为1或者2,P为事故发生的概率,其二分类Logistic函数为
(2)
由于事故发生受到多种因素影响,即事故发生的概率模型存在多个自变量x1,x2,…,xn,将P与x1,x2,…,xn建立线性关系,可以得到某交通情况下对应的事故发生概率计算如下:
(3)
xiβ=β0+x1iβ1+...+xkiβk
(4)
式中:P(xi)为交通运行中发生事故的概率;xiβ为影响事故发生变量的线性组合;β0为常数;β1,β2,…,βk为自变量的回归系数。其中β越大,则自变量与事故之间关联性越高。expβ为事故发生率,是自变量每增加一个单位,随之变化的事故发生率情况。
在选用Logistic概率模型拟合交通事故发生模型时,要遵循Logistic概率模型的假设条件:①数据必须来自于随机样本;② Logistic概率函数无法适用于多元共线性的变量,即如果自变量直接存在共线性关系会导致标准误差的膨胀;③ Logistic概率模型中因变量与自变量之间需非线性关系。因变量P(x)为二分变量,即变量只能取两个相互对立的值,例如0和1,是和否。
1.2 显著性检验模型
由于Logistic概率函数模型对输入变量有着极高的要求,预测的精度与输入变量的选取有着极大的联系,因此需要对模型的输入变量进行相关性检验,以提出相关性较低的变量以免影响预测结果。相关性检验方法有很多,一般适用于Logistic概率函数的有Score检验法和T检验法等。
Score检验是一种初始检验方法,是用于在建模之前根据变量之间特定关系,判断自变量与因变量相关程度的方法。Score检验值的计算公式为
(5)
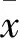
T检验是戈斯特为了观测酿酒质量而发明的。戈斯特在位于都柏林的健力士酿酒厂担任统计学家,1908年在 Biometrika上公布T检验。T分布理论来推断差异发生的概率,从而判定两个平均数的差异是否显著。T统计计算公式为
(6)
T检验中的p代表一种概率,是表示原假设为真的前提下,出现该样本或比该样本跟极端的结果的概率之和。一般取自由度为2,取p<0.05的参考变量为输入模型中的自变量。
2 基于Logistic模型的事故率模型分析流程
通过分析交通参数与事故间的关联性,构建预测模型,利用接收者操作特征(receiver operating characteristic,ROC)曲线探寻的阈值预测隧道内事故的发生。事故预测方法分析技术路线见图1。
(1)采集数据,采集事故发生前后以及正常交通状况下的交通参数。
(2)显著性分析,对提取的与事故相关的参数进行定性、定量的显著性分析。
(3)模型计算,利用处理后数据集对Logisitic模型自变量的回归系数进行计算。
(4)阈值确定,标定不同交通环境下预测模型中事故发生阈值。
(5)事故预测模型分析,将实时数据代入模型计算预测交通事故发生的可能并分析。
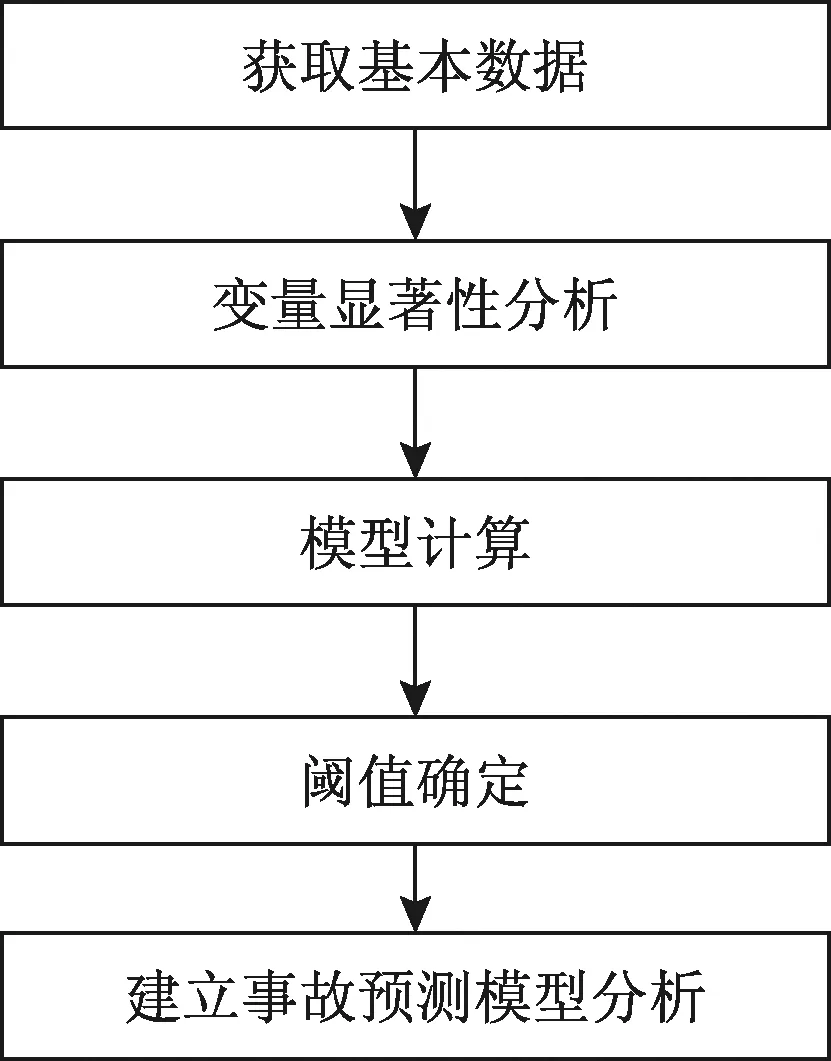
图1 事故预测模型构建技术路线Fig.1 Technical route for accident prediction model constructed
3 事故影响因素分析
3.1 数据来源
青岛胶州湾隧道路段设计时速为80 km/h,全线长约7 800 m,主线为单向3车道,内部最大坡度为4%,最小转弯半径为800 m,高峰时期单向流量约为4 000 veh/h。胶州湾隧道内大约每150 m设置有高清监控摄像机,共计172个,监控视频能够记录隧道内全天交通运行情况。
提取隧道内2018年5—6月交通监控视频,挑选出所有的交通碰撞事件视频,并利用视频处理技术采集非事故情况下及事故前10 min的交通流参数数据包含流量、速度、密度等以及车辆行为数据即不规则驾驶行为数据等。其中不规则驾驶行为包括车辆的急加速、急减速、违规换道、超速等行为。并且交通事故数据仅包含由交通状况或驾驶员因素导致的事故,例如追尾事故等,不包括由车辆原因导致的事故,如抛锚事故等。
3.2 特征参数分析
在综合调研现有研究成果的基础上,针对交通事故发生前的交通运行数据进行研究分析。利用胶州湾隧道内碰撞事故发生前事故车道的流量数据、速度数据以及车头间距数据进行统计分析,详见图2~图4。
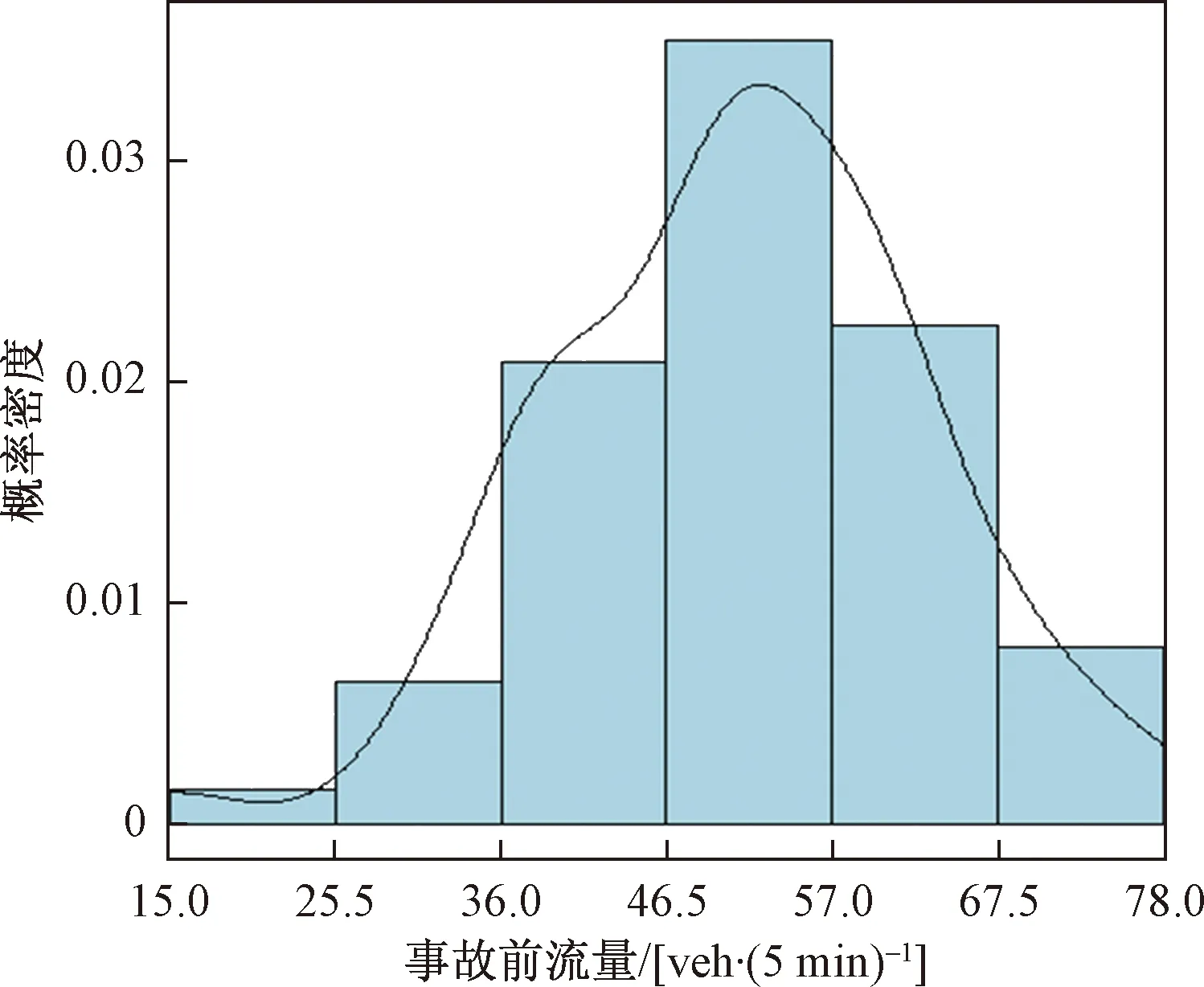
图2 事故发生前流量统计直方图Fig.2 Flow statistics histogram before the accident
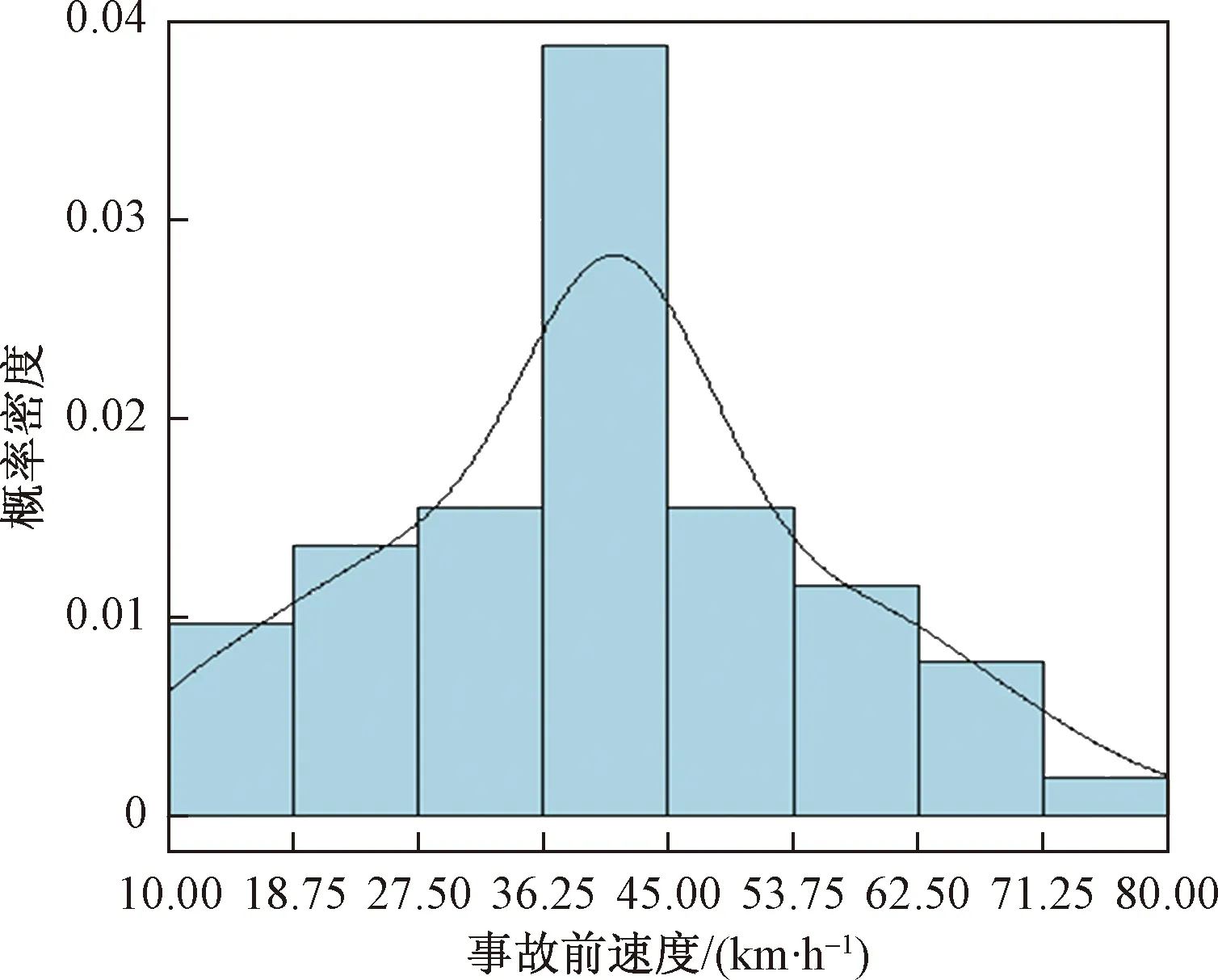
图3 事故发生前速度统计直方图Fig.3 Speed statistics histogram before the accident
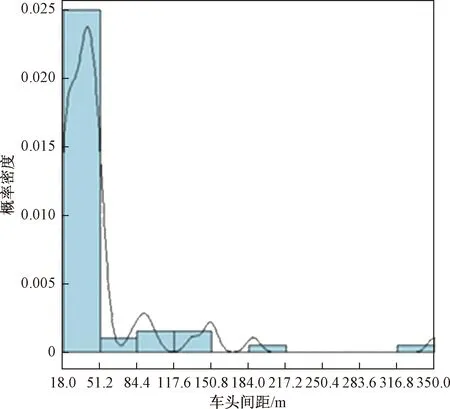
图4 事故发生前车头间距统计直方图Fig.4 Space headway statistics histogram before the accident
由图2~图4可见,事故前5 min流量统计拟合分布曲线接近正态分布,呈现集中分布趋向,说明流量变化与事故发生可能存在关联,同时另外处理了事故前10 min流量数据分析,结果显示存在峰值但分布较为平缓。事故前5 min平均车辆速度分布趋向于正态分布,且事故前速度分布存在高峰,较流量数据而言,分布的峰值更大,可以看出速度与交通事故发生更可能存在关联性。车头间距同样是交通运行中的重要参数,合适的车头间距是避免交通事故发生的主要条件之一。综上,从事故前交通参数统计分布可以看出交通事故发生前交通状况存在相似性,证实了事故预测的可能性。
依据大量视频数据观测,不规则行为与交通事故发生有着密切的联系,大部分交通事故的发生,主要原因在于驾驶员的驾驶行为不规范。统计急减速、换道行为、异常慢速行为3种车辆不规则行为。为描述总体交通运行状态中驾驶行为的安全性,提出车辆不规则行为率(ρ)的概念,详见式(7)。
ρ=y/q
(7)
式(7)中:ρ为不规则行为率;y为不规则行为数(次/5 min);q为5 min流量值。
结合现有成果以及胶州湾隧道相关数据的分析,通过初步筛选,提取了交通事故前的交通运行特征参数,见表1。

表1 事故前交通运行特征参数Table 1 Parameters of traffic moving charac-teristics before the accident
根据前期的调研分析发现事故前10 min的交通运行状态对交通事故的发生具有一定的影响,而事故前5 min的流量数据通过上述分析,可以用于交通事故预测分析。因此提取事故前5 min事故前10 min的交通流数据。
3.3 特征变量显著性检验
鉴于Logistic概率函数模型的应用条件,为保证模型建立的精确性,需要针对交通特征参数变量进行相关性分析,剔除在检验分析中显著水平低的变量。利用Score检验法以及T检验法对交通流特征变量与事故发生之间的密切程度进行定量计算,对初选变量进行关联性分析,详细见表2、表3。
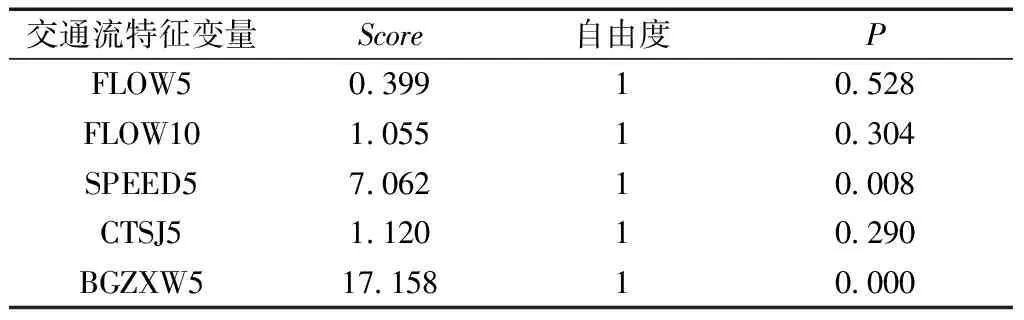
表2 交通流特征变量的Score检验结果统计表Table 2 Score test results statistics table of traffic flow characteristic variables
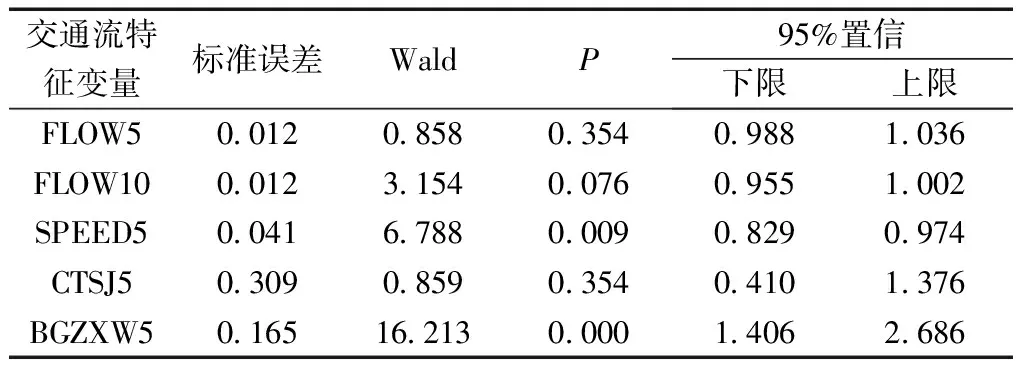
表3 交通流特征变量的T检验结果统计表Table 3 T test results statistics table of traffic flow characteristic variables
建模计算中因变量的编码规则有0、1,表示交通事故的发生与否,交通事故发生则其因变量值为1,没有发生交通事故则其因变量值为0。根据因变量的编码规则以及自变量值,很容易计算出交通流特征变量的Score值,由表2可看出事故前5 min流量(FLOW5)、事故前10 min流量(FLOW10)以及事故前5 min车辆的平均车头时距(CTSJ5)得分较低,但是事故前5 min平均速度(SPEED5)以及事故前5 min的车辆不规则行为率(BGZXW5)Score检验值满足一般的要求。表3中,Wald为卡方值,即回归系数与标准误差比值的平方值,由于其临界值模糊,需要参考P值,以判断显著性。由表3可知,仅有事故前5 min平均速度(SPEED5)以及事故前5 min的车辆不规则行为率(BGZXW5)的P<0.05,其他变量的P≥0.05。综上,由于SPEED5、BGZXW5的显著性水平较高,应当在模型中保留,其他变量可以剔除。
4 模型构建及应用
4.1 样本数据准备
利用视频处理技术采集2018年5—6月期间共118组数据进行分析和处理,其中包括非交通事故数据63组以及交通事故数据55组。通过事故影响因素分析确定模型变量包含事故前5、10 min流量数据、事故前5 min速度数据、事故前5 min平均车头时距以及不规则驾驶行为数据等,详见表4,其中Num表示提取视频的时间及摄像头编号;ACCIDENT表示事故是否发生,1为发生事故,0为无事故发生。并且交通事故数据仅包含由交通状况或驾驶员因素导致的事故,例如追尾事故等,不包括由车辆原因导致的事故,如抛锚事故等。
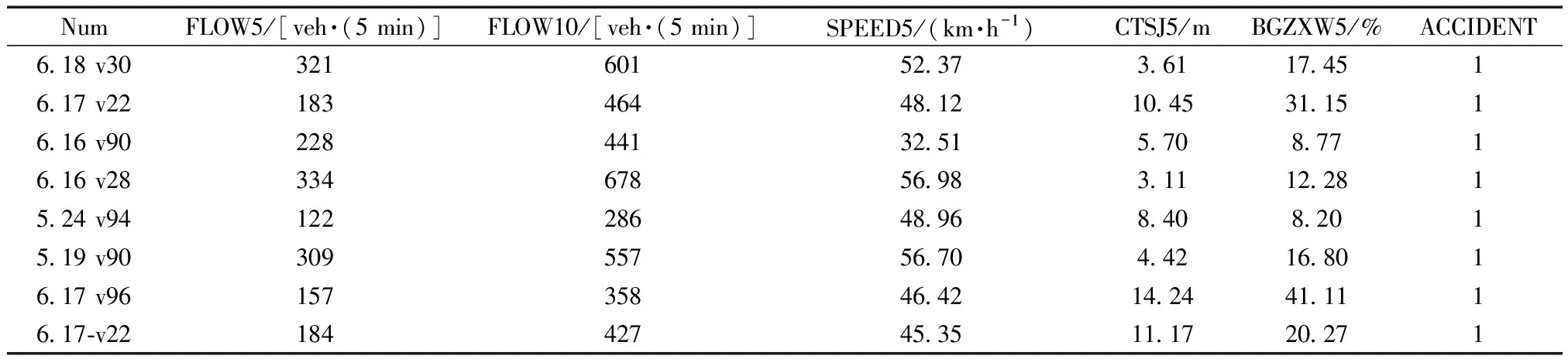
表4 交通事故数据样表(训练集)Table 4 Traffic accident data sample table (train set)
通过随机抽取的方式将样本分为独立的两个部分,即训练集和验证集,其中训练集30组事故数据和40组非事故数据,占总样本的60%,验证集由25组事故数据和23组非事故数据组成,占总样本的40%。训练集是用来求解模型参数,构建事故预测模型;测试集是用于检验模型的事故预测准确性。
4.2 Logistic概率模型求解
对交通流特征变量进行显著性检验分析后,最终模型的显著变量仅有SPEED5、BGZXW5两个自变量和一个常数量。代入胶州湾隧道训练集的事故前5 min的速度数据以及事故前5 min不规则行为率,利用最大似然法求解变量参数,得到结果如表5所示。
其中SPEED5系数为负,显示事故发生前5 min内事故点处速度相对于非事故情况速度低,即说明隧道内运行速度越小,事故发生的可能性越大。BGZXW5系数为正,表示事故发生前5 min内车辆的不规则行为相对比非事故情况下要大,即不规则行为越多,隧道内发生事故的可能性就越大。
依据最大似然法求解结果可以得到,以速度与不规则行为率为因子建立事故率预测Logistic概率模型:
xβ=2.101-0.103x1+0.579x2
(8)
(9)
对估计的模型进行拟合优度评价,评价结果见表6。
在自由度取2,显著水平为0.05,可以得到卡方临界值为5.991。因此,最大似然对数值检验通过。计算的广义决定系数也较大,说明模型的拟合优度教好,建立的事故率预测Logistic概率模型能过较好的预测交通事故的发生。

表5 模型系数求解Table 5 Model coefficient solving

表6 模型拟合结果Table 6 Model fitting results
注:2lg likelihood为最大似然平方的对数值,Cox & Snell R Square为广义决定系数,Nagelkerke R Square为伪决定系数。Nagelkerke拟合优度是一种校正后的Cox & Snell拟合优度。
4.3 模型阈值确定
Logisitic模型预测结果是0-1的概率,因此在实际运用时,针对这种二分类问题选择合适的阈值以此判断事故情况或正常交通情况的概率输出范围至关重要。因为高阈值通常无法识别很多事故的潜在条件,而低阈值会错误的将正常交通状况预警为高事故风险情况,给出错误的预测结果。利用绘制接收者操作特征(receiver operating characteristic,ROC)曲线的方法来寻找最合适的阈值。ROC曲线是以真阳性率(灵敏度,TPR)为纵坐标,假阳性率(1-特异度,FPR)为横坐标绘制的曲线。灵敏度指把实际为真值(事故)判断为真值(事故)的概率,特异性指把实际为假值(正常情况)判断为假值的概率。
表7是以0.5为阈值训练集的预测结果,其中TN为正确拒绝的非匹配数目;FP为误报;FN为漏报;TP为正确肯定的数目。由表7便可以得出阈值为0.5的ROC曲线横、纵轴坐标(FPR,TPR),其中FPR=FP/(FP+TN),TPR=TP/(TP+FN)。随着阈值的逐渐减小,越来越多的实例被划分为真值(事故),但是这些真值(事故)中同样也掺杂着假值(正常情况),即TPR和FPR会同时增大。阈值最大时,对应坐标点为(0,0),阈值最小时,对应坐标点(1,1)。预测精度最高即准确率为100%,在ROC曲线图中对应为理想阈值点:TPR=1,FPR=0,即ROC图中(0,1)点,故ROC曲线越靠拢(0,1)点,越偏离45°对角线越好。
Logisitic模型ROC曲线,见图5。可见阈值在0.36左右时,预测效果最好,这时TPR值为0.75,FPR值为0.26。因此本文的阈值确定为0.36,当预测值大于等于0.36时,判定为高事故风险;当预测值小于0.36,判定为正常交通状况。

表7 训练集预测结果Table 7 Predicted results of train set
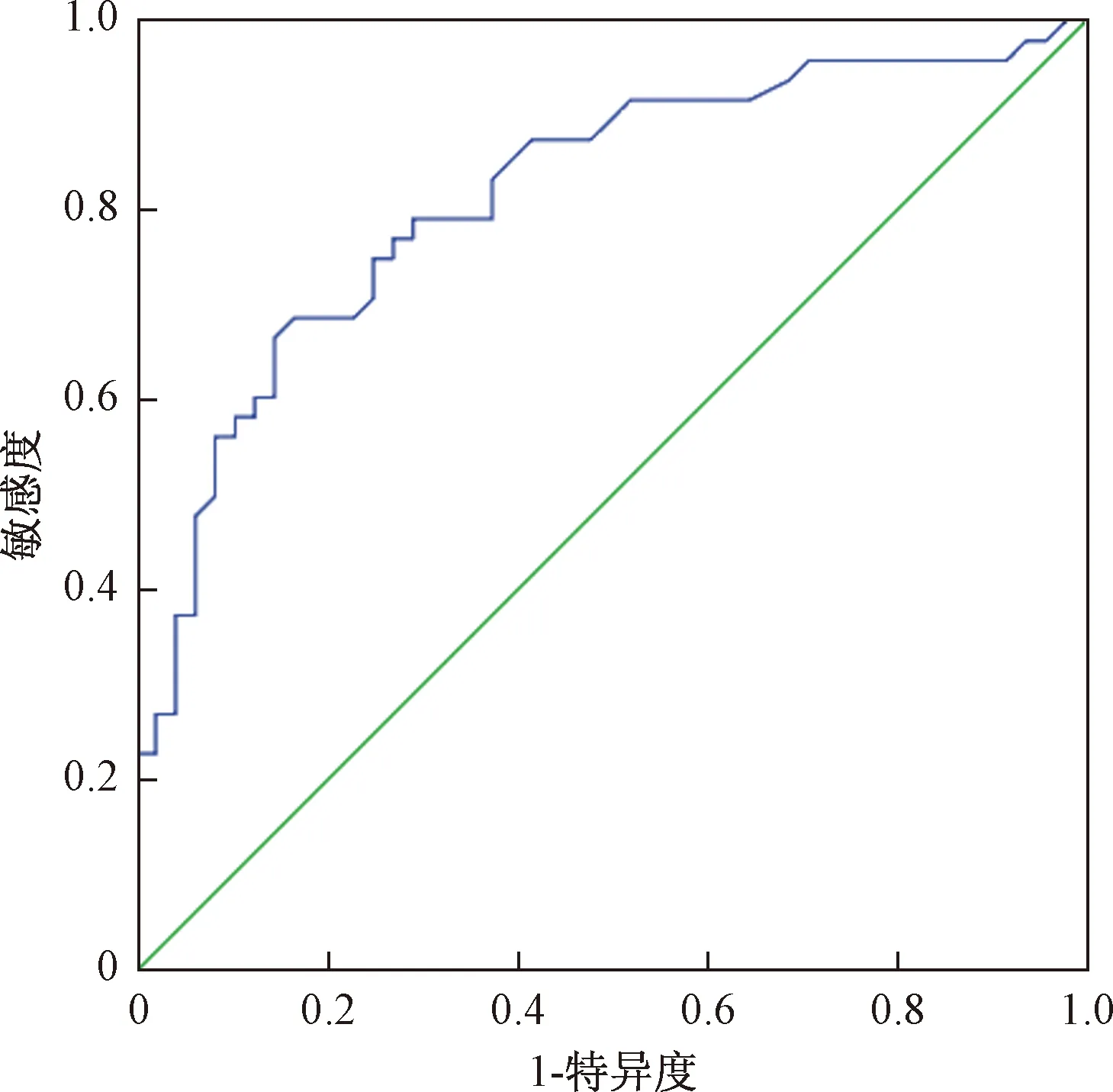
图5 模型预测的ROC曲线Fig.5 Model predicted ROC curve
4.4 实例验证
利用青岛市胶州湾隧道内2018年5—6月随机挑选的48组交通事故的视频数据,采集相关交通参数进行预测分析,预测结果详见表8。从表8中可知在25个事故样本中,有22组样本被模型准确预测,预测准确度达到88%;在23个非事故样本中,有15组预测结果符合实际,预测准确度达到65.2%,结果表明事故预测比非事故预测有较高的准确度,Logisitic模型在城市隧道中在预测由交通状态或驾驶员原因发生的交通事故(如追尾事故)方面有较高的预测准确度。验证集共48组数据,预测准确有37组数据,可看出Logisitic预测模型的准确性为78.4%。

表8 模型预测结果Table 8 Model prediction results
5 结论
基于青岛胶州湾隧道相关数据,选用Logistic概率模型建立隧道交通事故率预测方法。Logistic概率模型将事故发生的潜在可能性量化,给管理者以更加直观的方式说明交通潜在的危险,为隧道内安全运营管控提供指导。
(1)通过对隧道内事故发生的相关因素研究,表明影响交通事故最主要的因素为交通运行速度以及车辆的不规则行为率,其中不规则行为率对事故发生的影响最为显著,隧道管理者可通过及时的诱导措施,降低隧道内事故的发生的可能。
(2)通过绘制ROC曲线的方法确定模型阈值,结果显示阈值为0.36,模型精度较高。
(3)通过胶州湾隧道交通事故数据整理的验证集数据评价事故率预测模型的准确率约为78.4%。
可见在可接受的误差范围内,提出的事故率预测模型预测结果可以为隧道内事故的应急救援处理提供一定的决策信息,同样也为隧道内管理提供有效依据。由于事故发生是多元素多方面的,不同的交通运行环境下导致事故发生的原因也是多样的,因此下一步将基于本研究,对模型进行优化,使得模型能够根据不同情况下自优化,以提高预测精度。

