基于嵌入式离散裂缝和扩展有限元的裂缝性页岩油藏流固耦合高效数值模拟方法

牛 骏, 苏建政, 严 侠, 汪友平, 孙 海

(1.国家能源页岩油研发中心， 中国石化石油勘探开发研究院，北京 100083；2.中国石油大学(华东)石油工程学院，青岛 266580)

页岩油气作为一种不可或缺的非常规油气资源，是目前研究和开发的热点[1]。页岩油气藏储层致密，其渗透率非常低，一般必须经过大规模水力压裂才可以进行商业化开采[2]。压裂后的页岩储层，由于水力裂缝的存在使其在渗流机理和流动特征上均不同于常规储层，表现出明显的应力敏感特征，且具有较强的非均质各向异性，常规基于修正绝对渗透率的应力敏感模型已不适用，亟需建立渗流场和应力场耦合的流固耦合模型[3]。然而，相比于常规连续性储层，页岩油藏由于水力裂缝的存在，导致流动和力学性质发生较大变化，流固耦合效应更明显，处理难度更大，常用的裂缝性储层流固耦合数学模型有：等效连续介质模型[4-5]、双重介质模型[6-7]和离散介质模型[8-9]。

等效连续介质模型将裂缝性介质看作一个连续体，首先需要判断表征单元体的存在性，并确定其大小，再计算等效渗流和力学参数表征裂缝对流固两场的影响，在此基础上根据成熟的连续介质力学理论进行耦合流动分析，模型数据需求简单而且计算效率高，一直以来在裂隙介质的水力学研究中占据重要地位。然而，由于等效连续介质模型过于简化、等效参数计算不够准确(尤其对于多相流问题)，无法准确刻画裂缝性介质中的多种流动模式共存特征，因此，在油藏实际应用中其分析结果往往误差较大；双重介质模型最早由Barenblatt等[6]建立，Warren等[10]对其进行了简化和推广，此后众多学者将多孔弹性力学与双重介质模型相结合用于裂缝性介质流固耦合研究，这类模型将裂缝系统和基岩系统之间的物质交换考虑在内，可以实际地模拟裂缝内的优先流现象。然而被裂缝分割成的基质岩块系统被假定具有规则的大小和形状，过于简化却不能充分表现出裂缝性介质的不连续性、各向异性等特点，同时基岩和裂缝间的窜流系数也难以准确获取(尤其对于多相、非稳态问题)，此外该模型仅适用于高度发育、空间尺度跨越小的裂缝性介质；离散介质模型对裂缝显示表征，能够反应裂缝对渗流场与应力场的影响。由于裂缝开度和油藏尺度相差极大，需要对裂缝进行降维处理，以防裂缝周围局部加密而增加网格量。然而裂缝两侧的位移场具有间断性，裂缝降维后采用常规数值方法难以有效解决，对此学者提出了相应的解决方法，主要分为以下三类：界面双节点单元法[11]、位移不连续法[12]和扩展有限元法[13]。界面双节点单元法在常规有限单元法的基础上，在裂缝单元节点处新增一个额外节点，反映裂缝两侧变量的不连续性。该方法求解较简单，但其网格划分和编号存在一定难度，并且数值求解稳定性和收敛性较差。位移不连续法作为一种边界元方法，求解简单、网格量小、精度较高，但其仅适用于均质储层，对于实际强非均质各向异性储层难以推导解析解建立离散格式，并且该方法最终形成的系数矩阵为满秩矩阵，对于大规模问题的求解难度大。扩展有限元法在标准有限元框架下，在连续区域内采取标准有限元方法，在包含不连续边界的区域内，增加间断形函数以修正有限元的位移近似函数，采取水平集方法来描述间断界面，使间断的描述独立于有限元网格，避免了以裂缝为约束的复杂非结构网格划分，但扩展有限元作为一种改进的有限元方法，其方程离散为全局离散，不满足单元的局部物质守恒，因此对于渗流方程(尤其多相流)，其计算精度较差。

近些年来，Yan等[14]基于等效连续介质模型和嵌套离散裂缝模型，提出了一种有效的数学模型来模拟含多尺度裂缝和溶洞的裂隙型多孔介质中流体力学耦合问题；张世明等[15]基于离散介质模型，提出了一种求解裂缝性介质等效渗透率的新方法；李友全等[16]基于离散介质模型，对致密油藏压裂直井进行了动态分析；孙若凡等[17]基于双重介质模型，对致密油藏压裂水平井进行了模拟分析；盛茂等[18]基于双重介质模型，建立了一种裂缝性页岩气藏的流固耦合模型并采用有限元法进行数值求解。然而目前并没有基于离散介质模型并使用扩展有限元法求解的研究。于是，将扩展有限元法与嵌入式离散裂缝模型[19]相结合，建立一种适用于裂缝性页岩油藏流固耦合数值模拟的新方法，该方法可以考虑裂缝开度的变化以及裂缝内流压对开度变化的影响，分别采用扩展有限元和模拟有限差分[19-20]求解力学和渗流方程，模拟有限差方法适用于强非均质各向异性储层，且具有良好的局部守恒性，可以准确求解压力场和速度场。嵌入式离散裂缝模型网格划分与扩展有限元类似，无需考虑储层内的裂缝形态，大大降低了网格划分难度，其计算精度与基于匹配性非结构网格的常规离散裂缝模型基本一致。

1 流固耦合数学模型

基于二维单相流固耦合问题来阐述本文数值模拟方法的原理与思想。假设在耦合流动过程中温度恒定，考虑基岩和流体的压缩性，基岩与裂缝中的流体流动均满足达西定律，岩石变形为微小线弹性变形，不考虑惯性力。采用常规多孔介质弹性力学符号约定，即拉伸为正，压缩为负。

1.1 岩石变形数学模型

(1)

σ=σeff-αpmI

(2)

(3)

(4)

σ·nf=-pf·nfon Γf

(5)

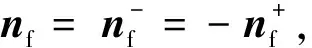
图1 裂缝性介质及其内、外边界示意图Fig.1 The sketch of a fractured porous medium and its boundaries

1.2 嵌入式离散裂缝模型

基岩系统流动数学模型：

(6)

(7)

(8)

裂缝系统流动数学模型：

(9)

(10)

式中:vm和vf分别为基岩和裂缝内渗流速度，m/s；km和Kf分别为基岩和裂缝渗透率，m2；μ为流体黏度，mPa·s；ρl为流体密度，kg/m3；φ为基岩孔隙度；Ks和Kl分别为岩石颗粒和流体的体积模量，Pa；εv为基岩体积应变；qm和qf分别为基岩和裂缝的源汇项，s-1；Vm和Vf分别为基岩和裂缝的单元体积，m3；bf0和bf分别为裂缝初始和目前的开度，m；qmf为基岩与裂缝间的窜流量，m3/s；qff为相交裂缝间的窜流量，m3/s；δ为狄克拉函数；qmf、qff、δmf和δff的详细计算格式和取值方法见参考文献[19]；Γq为流量外边界，Γp为定压外边界，如图1所示。整个系统的初始压力为p0。

2 模型离散求解

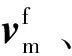
图2 网格单元数值离散及自变量分布示意图Fig.2 The schematic of discretization and locations of the solution variables

2.1 扩展有限元离散力学方程

扩展有限元根据单位分解法[21](PUM)的思想，在常规有限元连续位移场的基础上，增加不连续位移场(裂缝段采用Heaviside函数，裂缝尖端采用尖端渐进函数)来表征计算区域内的位移间断特性，因此，其单元位移的近似解可以表示为

H[φ(xi)]}ai+

(11)

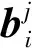
(12)

H(ξ)=1, ∀ξ>0 andH(ξ)=-1, ∀ξ<0

(13)

F(r,θ)=

(14)

将式(2)代入式(1)，考虑边界条件[式(4)和式(5)]，得到方程(1)的积分弱形式为

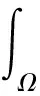
(15)

式(15)中：δu为位移试函数；δu+和δu-分别表示裂缝正负两侧的位移试函数，如图1所示。

裂缝壁面发生相对位移后，裂缝开度及渗透率(立方定律)表达式为

df=df0+(u+-u-)·nf

(16)

(17)

在扩展有限元中，采用水平集方法[22]确定裂缝的几何信息，同时采用高斯数值积分方法计算单元和边界上的积分，而对于裂缝穿过的单元，常规的高斯积分方法不适用，需要根据裂缝形状对这些单元进行单元分解，再在每个分解子单元内进行数值积分。

2.2 模拟有限差分离散渗流方程

(18)

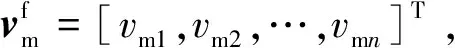
对于方程(7)，在基质网格单元上积分且应用散度定理得

(19)

考虑裂缝渗透率为标量且为一维流动，因此采用有限差分进行离散。将方程(9)代入方程(10)，方程左右两端同乘裂缝网格单元体积得

(20)

2.3 整体计算格式

以存在一条裂缝为例，考虑基岩网格单元边界面上的速度连续，将力学方程和渗流方程的数值离散格式组装到一起，得到嵌入式离散裂缝流固耦合模型数值计算格式为

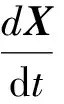
(21)

(22)

(23)

式中:Ku为扩展有限元位移刚度矩阵；Qum和Quf分别为基岩和裂缝的流固耦合系数矩阵；Km为基岩模拟有限差分系数矩阵；Tmf为基岩与裂缝窜流系数矩阵；Kf为嵌入式裂缝有限差分系数矩阵；Sm和Sf分别为基岩和裂缝的压缩项系数矩阵；u、a和b分别为节点位移和额外未知量，整体对应于系数矩阵A的第一行；vm、pm和πm分别为网格边界流速、网格中心压力和网格边界压力，整体对应于系数矩阵A的第二行；pf为裂缝单元压力；C为体积力载荷、边界应力载荷以及基岩和裂缝源汇项列阵。

对于方程(21)中的时间导数项，采用全隐式差分格式进行离散。

(Adt+B)Xn+1=BXn+Cdt

(24)

式(24)中：n表示第n个时间步；dt为时间步长。

3 算例分析

首先分别通过与一维多孔介质和二维裂缝性介质流固耦合问题的解析解和精细网格数值解进行对比，验证所提方法的正确性；然后分析不同条件下裂缝开度的变化情况以及裂缝开度变化对耦合流动的影响；最后对于某一二维页岩油藏弹性开采进行数值模拟，对比基岩渗透率为对角张量和全张量时的差异，说明所提方法对于全张量渗透率的适用性。本文算例均采用平面应变假设。

3.1 模型验证

考虑如图3(a)所示的深度200 m的一维流固耦合模型，初始流压和位移均为0，在上、下边界同时施加100 kN/m2的恒定边界载荷，左、右边界封闭，上、下为边界定压(压力为0)，模型参数如表1所示。采用所提方法对该一维模型进行数值求解并与其解析解进行对比，图3(b)给出了不同时刻流体压力的数值解与解析解对比结果(由于模型上、下对称，图中只给出了上半部分的压力对比)，能够看出数值解与解析解基本一致。

表1 模型基本参数Table 1 The model basic parameters

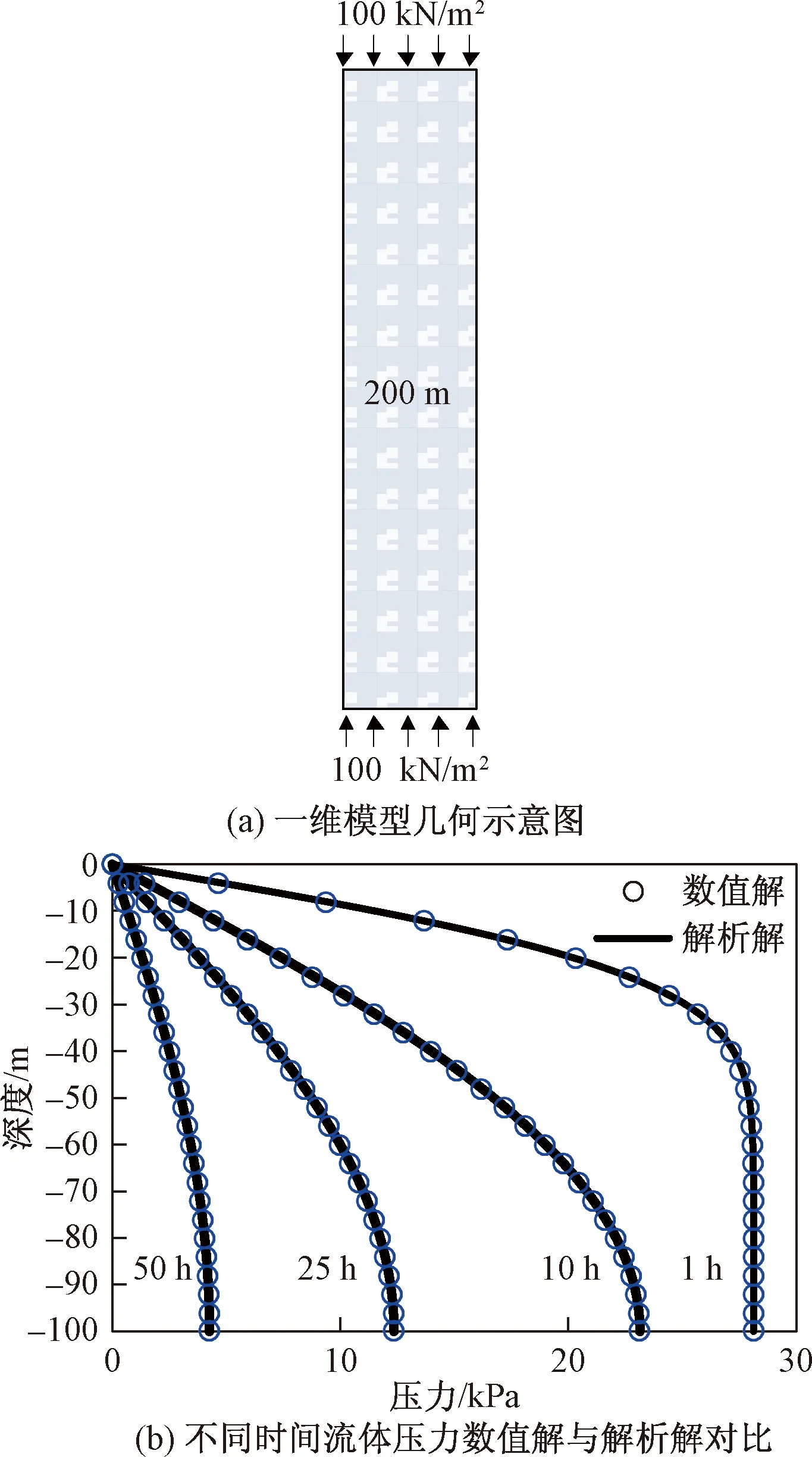
图3 一维模型几何示意图及不同时间流体压力数值解与解析解对比Fig.3 The sketch of a 1D model and the comparison of numerical solution and analytical solution of fluid pressure at different times

如图4(a)所示，为一10 m×20 m 的裂缝性介质模型，其中裂缝长10 m、开度0. 001 m，垂直位于模型区域中心。初始流压和位移均为0，模型的力学边界条件如图4(a)所示，渗流边界条件为：上边界定压(压力为0)，其余边界封闭。裂缝孔隙为1.0，初始渗透率为8.33×10-8m2，其他参数如表1所示。由于裂缝的存在，该模型难以推导解析解，因此，将裂缝显示处理，通过在裂缝周围进行局部网格加密构建精细网格，如图4(b)所示，采用有限单元法求解作为参考解。图4(c)为所提方法采用的计算网格，可以看出其网格划分难度及网格数量都大大降低。

不考虑裂缝开度变化，分别采用精细网格有限元方法和所提方法对该裂缝性介质流固耦合模型进行模拟，图4(d)和图4(e)分别为模拟10 000 s后两种方法得到的压力场图，图5(a)和图5(b)分别给出了两种方法计算得到的测试点A和B处压力和y方向位移随时间的变化曲线对比。通过对比可以看出，所提方法的计算结果与精细网格有限元方法参考解基本一致。因此，本节的两个算例验证了所提方法的正确性。

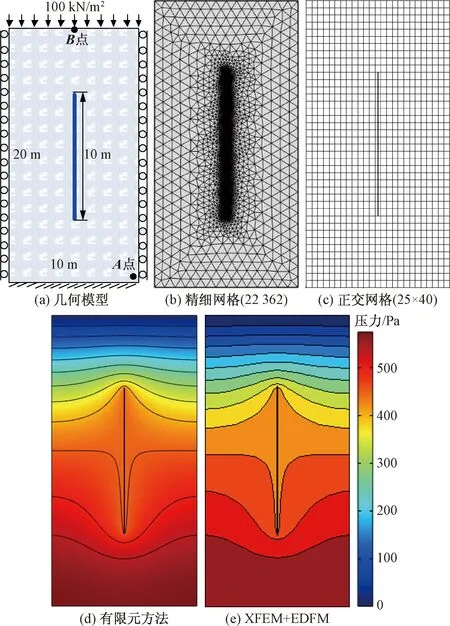
图4 裂缝性介质模型示意图、不同方法网格划分结果及模拟10 000 s后压力场图Fig.4 The model and grids of a fractured medium, pressure distribution after 10 000 seconds for different methods

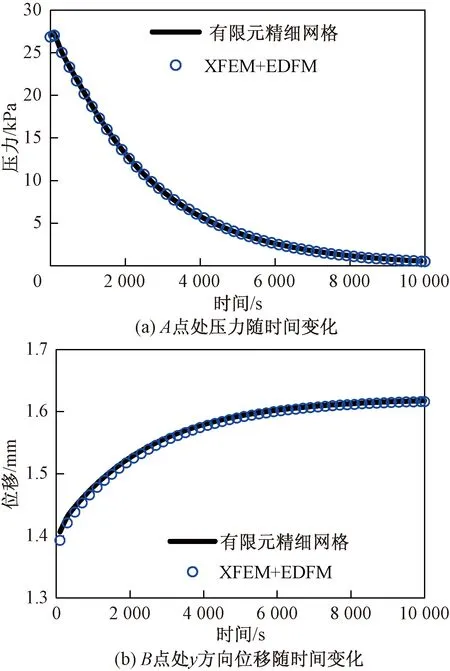
图5 两种方法计算得到的测试点压力和位移随时间变化曲线Fig.5 Pressure and displacement (y) the test point various time obtained from two methods

3.2 裂缝开度随时间变化

由于本文模型分别采用嵌入式离散裂缝和扩展有限元中将裂缝的渗流和力学特征显示表征，因此可以有效刻画裂缝开度随时间的变化情况以及裂缝开度变化对耦合流动的影响。基于图4(a)所示的裂缝多孔介质模型，模型参数与上一个算例一致，不考虑裂缝内流体压力的影响，分别采用所提方法和精细网格有限元方法计算100、2 000、10 000 s时的裂缝开度分布，结果如图6(a)所示，能够看出两者结果基本一致，验证了所提方法用于计算裂缝开度的正确性。图6(b)给出了不考虑与考虑裂缝内流体压力影响两种情况下所提方法计算得到的不同时间裂缝开度分布，可以看出模拟100 s时，两者裂缝开度相差很大，随着模拟时间增长，两者之间的差距逐渐减小，到模拟10 000 s时，两者裂缝开度基本一致。这是由于早期裂缝内流体压力较高，考虑其影响后对裂缝起到支撑作用，可以有效阻止裂缝闭合，随着模拟时间增长，裂缝内的流体压力逐渐减小，其支撑作用逐渐减弱。

图6 不同时间裂缝开度分布Fig.6 Fracture aperture distribution at different time

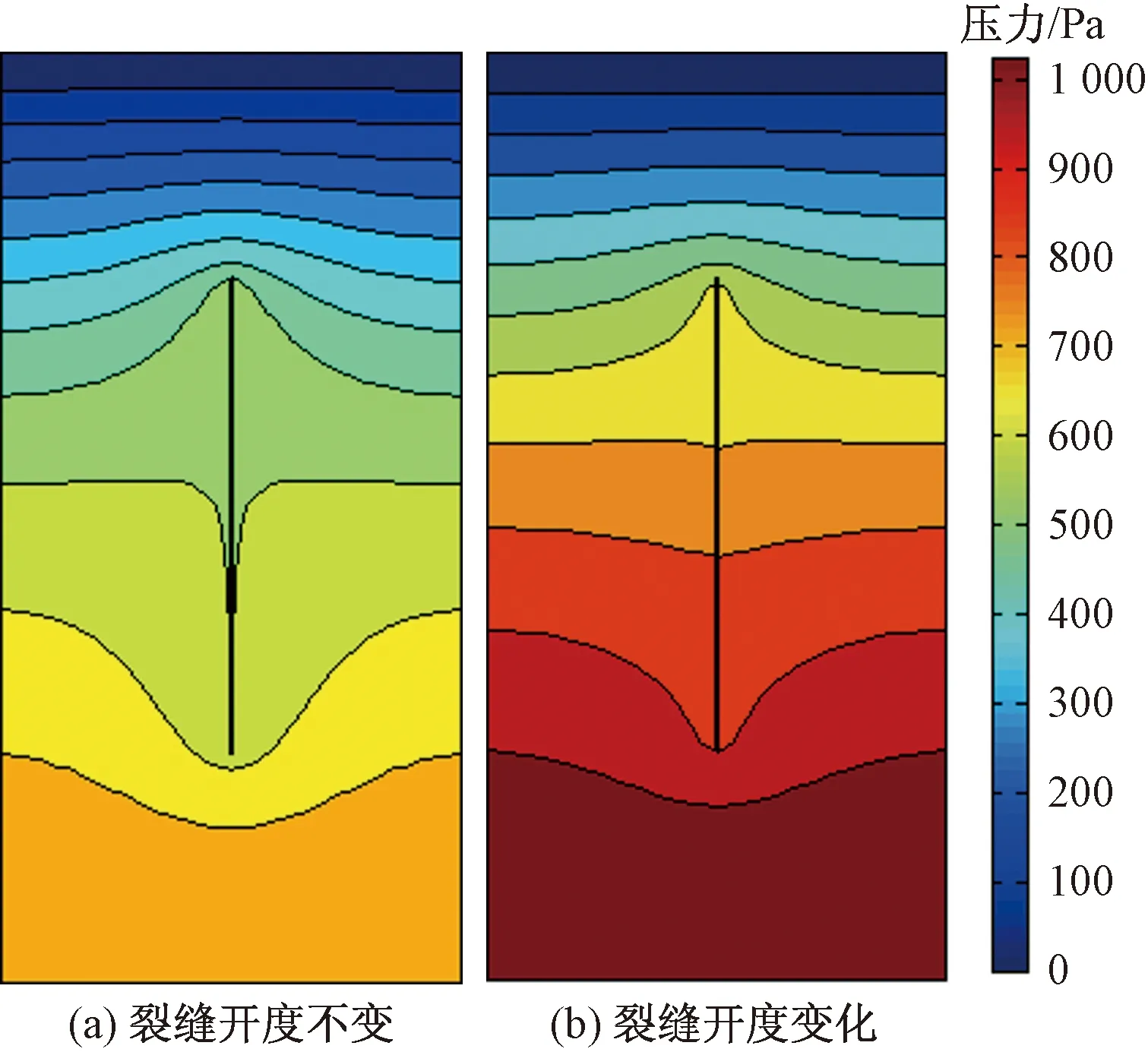
图7 模拟10 000 s后的压力场分布图Fig.7 Pressure distribution after 10 000 seconds

在以上模型的基础上，将上边界载荷增加到200 kN/m2，其他模型参数和条件均不变。采用所提方法分别对裂缝开度不变和变化两种情况下的流固耦合进行模拟，图7(a)和7(b)分别给出了模拟10 000 s后两种情况下压力场分布，图8给出了两种情况下A点处压力及两者误差随时间的变化曲线，可以看出：考虑裂缝开度变化后，随着模拟时间增加，裂缝开度和导流能力逐渐减小，流体流出速度减小，区域内的流体压力增加，两者相对误差逐渐增大。

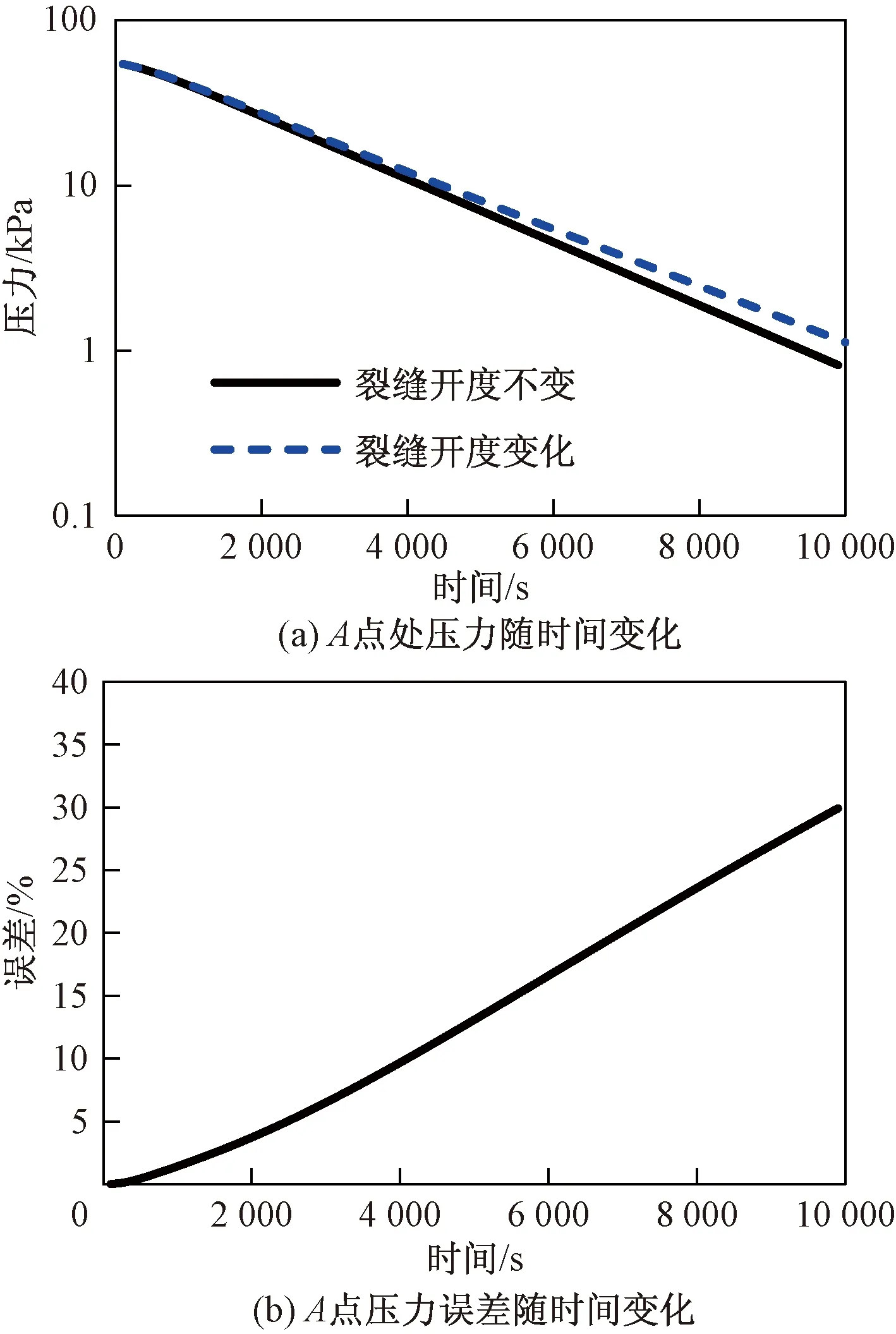
图8 两种情况下A点处压力及两者相对误差随时间变化曲线Fig.8 Pressure and relative error at point A for various time in the two cases

3.3 裂缝性页岩油藏弹性开采

图9 裂缝性页岩油藏模型示意图及网格划分结果Fig.9 The sketch of fractured shale reservoir model and meshing results

表2 页岩油藏基本参数Table 2 The reservoir parameters

图10～图12分别给出了基岩渗透率为对角张量和全张量两种情况下，模拟10 d后的压力场和x方向位移场图、不同裂缝的开度变化情况(裂缝1为最左侧裂缝，裂缝3为从左侧数第三条裂缝)以及累产随时间变化情况。可以看出，考虑全张量渗透率后，压力场、位移场、裂缝开度和累积产量相比于对角张量渗透率条件下的结果有一定变化，说明对于基岩渗透率为全张量的实际强各向异性储层，不能采用有限差分或有限体积等忽略非主对角线值的常规数值方法。

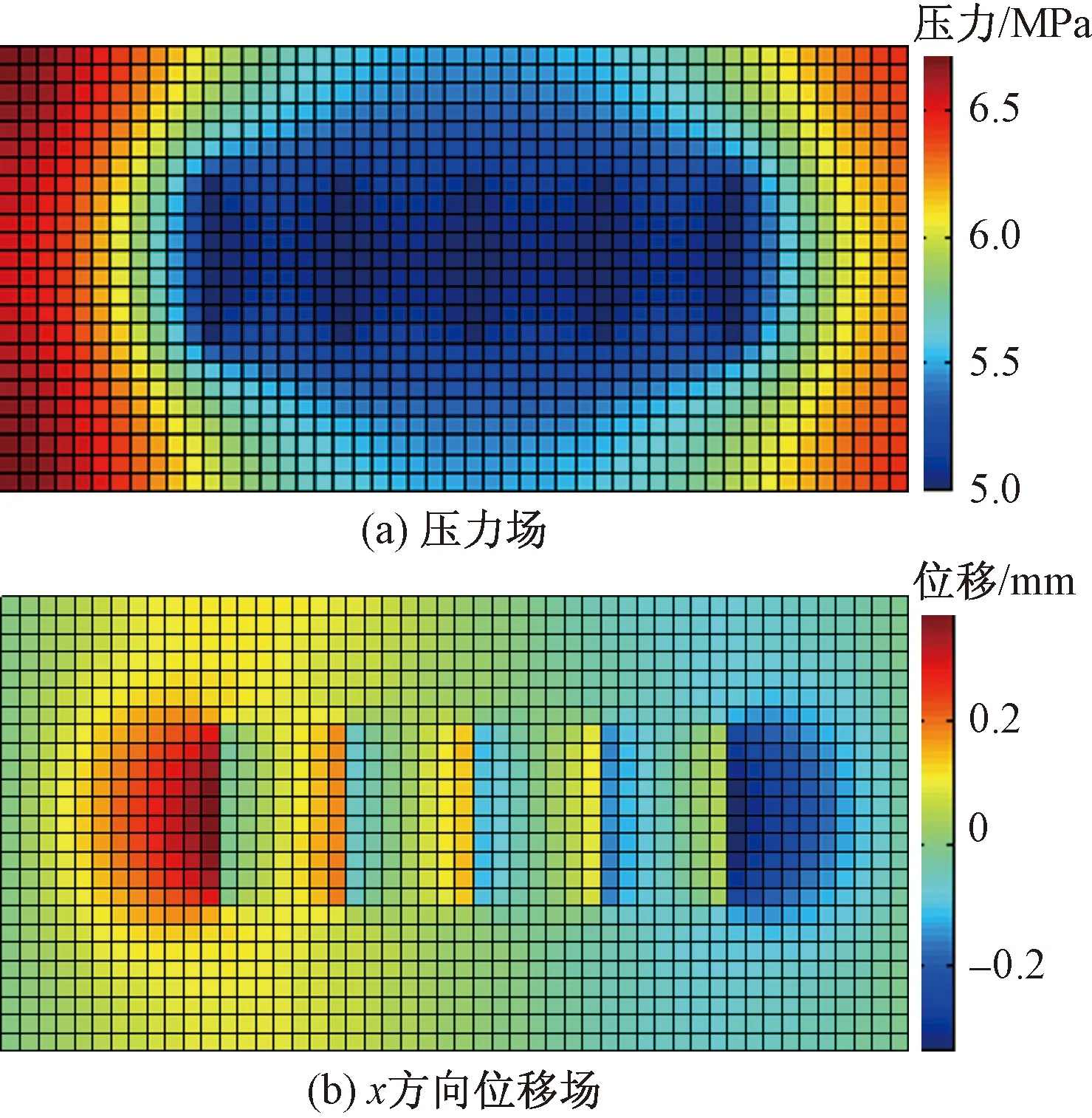
图10 对角张量渗透率下弹性开采10 d时压力场和x方向位移Fig.10 Pressure and displacement distribution after 10 days for diagonal-tensorpermeability

图11 全张量渗透率下弹性开采10 d时压力场和x方向位移Fig.11 Pressure and displacement (x) distribution after 10 days for full-tensorpermeability

图12 不同基岩渗透率条件下，模拟10 d裂缝开度和累产对比Fig.12 Fracture apertures and cumulative production for different matrix permeability on different bedrock permeability conditions after 10 days

4 结论

通过耦合嵌入式离散裂缝模型和扩展有限元提出一种适用于裂缝性页岩油藏的流固耦合高效数值模拟方法，该方法的创新性以及所取得的结论如下。

(1)该方法对裂缝使用降维显式处理，能够准确刻画裂缝对渗流场和应力场的互相影响，同时可以模拟裂缝开度的动态变化过程以及裂缝内流体压力对裂缝变形的影响。该模型划分网格时不必考虑裂缝几何形态，只需对基岩系统进行正交网格剖分，使得网格划分时的复杂度大幅降低。

(2)对于模型中流动方程求解采取模拟有限差分方法，满足局部质量守恒并且可以有效处理全张量形式渗透率；力学方程求解采取扩展有限元方法，可以准确处理裂缝两侧的位移间断性。

(3)分别通过与一维多孔介质和二维裂缝性介质流固耦合问题的解析解和精细网格数值解进行对比，验证所提方法的正确性，分析了不同条件下裂缝开度的变化情况以及裂缝开度变化对耦合流动的影响。

(4)针对一、二维裂缝性页岩油藏弹性开采进行了数值模拟，对比基岩渗透率为对角张量和全张量时的差异，说明所提方法对于全张量渗透率的适用性。