一种基于改进自抗扰控制器的风电机组变桨距控制策略

宋文静, 谢 源, 黄文君, 李容爽

(上海电机学院电气学院，上海 201306)

为了生态环境的进一步发展，人们对可再生能源的使用越来越关注，尤其是风力发电。由于风的随机性、波动性等特征，风电机组的输出功率也处于不断变化状态。风机并网后，风机输出功率的不断变化对电力系统集成、运行和控制造成重大挑战，特别是当有风电场向电网注入大量电力时，可能导致电网中的频率偏差。因此，越来越期望对叶片桨距角进行精确调整，有效控制风电机组的输出功率[1]。

传统PID控制器虽然在有精确模型的线性控制中取得了较好的效果，但对具有严重非线性的风电系统来说，传统PID控制效果并不符合人们的期望值[2-3]。因此，国内外学者对变桨控制策略深入研究，将一些模糊逻辑控制器、预测控制器、鲁棒控制器、自抗扰控制器(active disturbance rejection controller，ADRC)应用到风电变桨控制中，且取得较好的控制效果。文献[4]提出了针对风的随机性与风电机组的非线性特征，将Smith预估控制器与模糊控制器相结合的变桨距控制策略，能够有效调节永磁直驱风电机组的输出功率。文献[5]提出了一种利用模糊逻辑整定PID控制器的变桨距控制方法，当风速大于额定风速时，模糊PID控制器对风机桨距角进行调整，实现风电机组稳定的输出功率，但系统输出有5.9%左右的超调。文献[6]提出了一种基于前馈控制理论和预测控制理论的复合控制策略，考虑到风的随机性，采用卡尔曼算法估计风速，并加入一种前馈控制，有效抑制了风速扰动，加入预测控制器对塔顶位移进行控制，在该控制策略下，风电机组的调节功率性能及抗扰动性能显著提高。文献[7]提出了鲁棒经济模型预测控制的风力发电机变桨距控制策略，针对风力发电机的经济性目标以及风速误差可能导致传统控制的一系列问题，离线设计了线性反馈控制器和相应的鲁棒控制不变集，以保证风力发电系统的鲁棒性，该方法能有效提高风电机组输出功率的动态性能，并增加风电机组使用寿命。文献[8]提出了一种基于定量反馈理论的桨距角鲁棒控制策略，针对风机模型的不确定扰动，采用定量反馈的鲁棒控制器，减少了同步误差问题。文献[9-11]提出了以转速为输入信号的自抗扰变桨控制器，有低过冲、快速收敛、高精度和优异的抗干扰能力的特点。该控制器能够估计和补偿系统中未知的时变非线性和扰动，有效改善风力发电机组变桨距控制效果。文献[12]提出了一种DSP与自抗扰控制软硬件相结合的变桨距控制方法，该控制方法以风速和功率为输入信号，并加入一个选择开关，控制桨叶调节方向和大小，具有较强的工程适应性。

本文提出了一种基于改进自抗扰控制技术的变桨控制方法。采用了连续平滑的非线性函数对传统自抗扰控制器进行改进。以风机给定功率和系统输出功率作为控制器输入信号，经过对信号的估计及补偿，得到合适的桨距角值。

1 风力发电机组建模

1.1 风轮模型

当自然风带动风轮旋转时，由空气动力学可知，风轮从风中捕获的功率Pw为

(1)

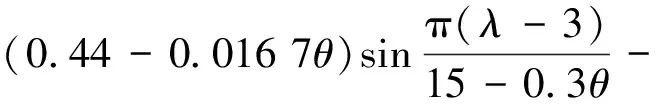
0.001 84(λ-3)θ

(2)

式中：ρ为空气密度；s为半径为R的风轮叶片扫过的面积；λ为叶尖速比；θ为桨距角；v为风速；Cp为风能利用系数。

1.2 传动系统建模

在直驱型风力发电机组中，由于没有齿轮箱，风轮机和发电机的轴直接连接。为了简化分析，忽略阻尼项。直驱风机的质量力学模型：

(3)

式(3)中：Tm为风轮机械转矩；Te为发电机电磁转矩；J为风机的转动惯量；ω为风轮转速。

1.3 永磁同步风力发电机建模

将风力发电机当作理想电机处理，则发电机基于d-q旋转坐标的数学模型为

(4)

式(4)中：ud、uq为d、q轴电压；id、iq为d、q轴电流；Ld、Lq为d、q轴电感；Ra为定子电阻；λ0为永磁体磁通；ωe为转子电角速度。

若Ld=Lq，发电机电磁转矩为

Te=1.5Npiqλ0

(5)

式(5)中：Np为发电机极对数。

1.4 变桨执行机构建模

目前兆瓦级风力发电机组变桨距执行机构大多采用液压装置和电机实现。可用式(6)表示：

(6)

式(6)中：τ为时间常数；θr为给定桨距角；θ为当前角度；s为拉普拉斯变换时的复变量。

2 基于改进型的自抗扰变桨控制器设计及仿真

当风速大于额定风速时，为保证风电机组的输出功率的稳定性，对叶片桨距角进行精确调整。当风速增加时，输出桨距角增大；当风速降低时，输出桨距角减小。自抗扰控制器是一种不依赖于精确模型的非线性控制器，该控制器能够估计和补偿系统中未知的时变非线性和扰动，有不错的抗扰性能及鲁棒性。但是，传统自抗扰控制器采用一个分段式的非线性函数进行设计，忽略了函数因在分界点处不平滑而导致的系统不稳定问题。针对这一问题，提出了一种基于改进自抗扰控制器的变桨控制方法。图1所示为改进自抗扰控制器的风机变桨距控制结构图。

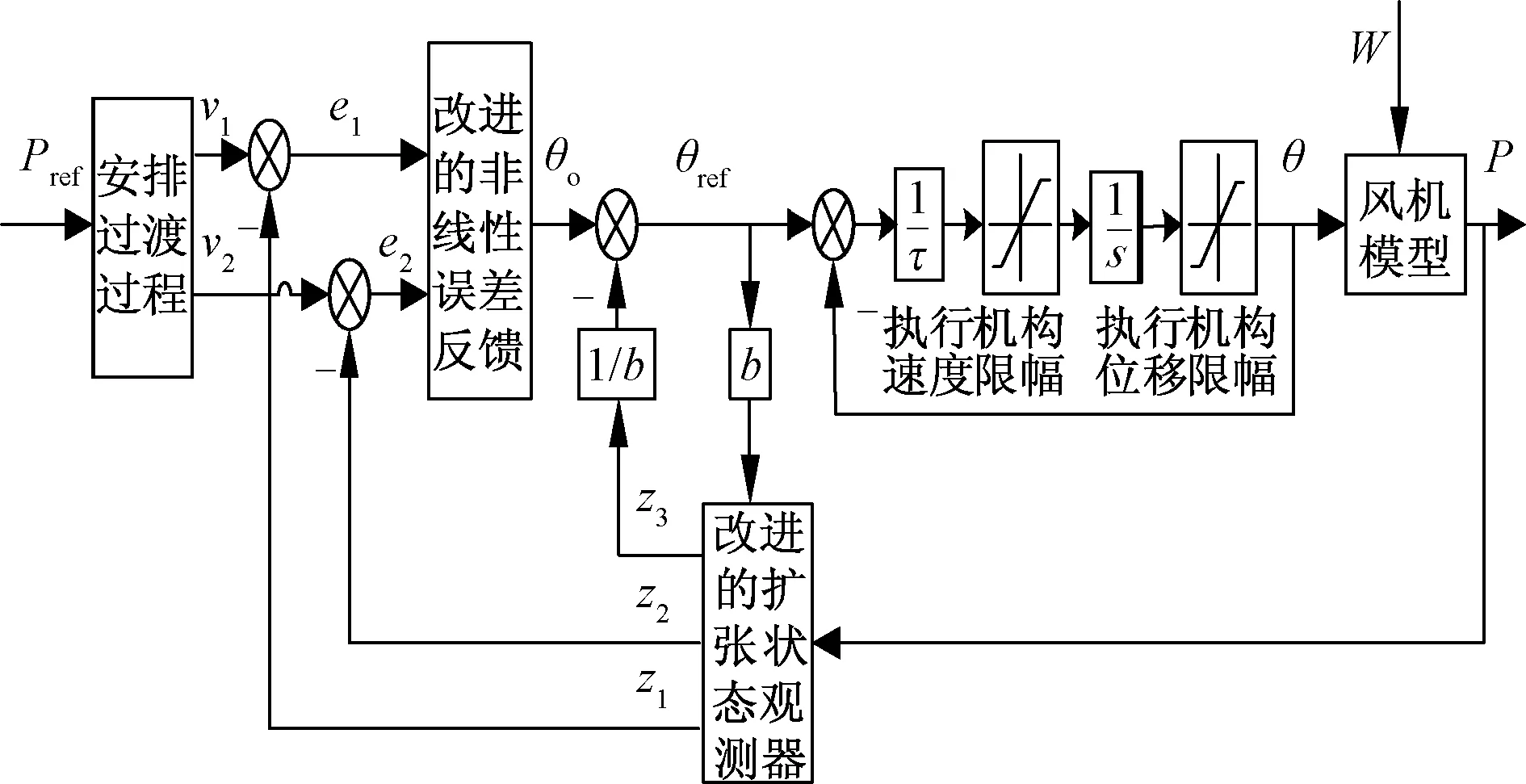
图1 改进型ADRC的风机变桨距控制结构图Fig.1 Improved ADRC wind turbine pitch control structure diagram

改进自抗扰控制器由跟踪微分器(tracking differentiator，TD)、改进的扩张状态观测器(extended state observer，ESO)以及改进的非线性状态误差反馈律(nonlinear state error feedback，NLSEF)组成。图1中，受控对象是风机，w是系统外部干扰，Pref是给定功率，V1是Pref的追踪信号，V2是V1的微分信号，P是输出实际功率，Z1是P的跟踪信号，Z2是Z1的微分信号，Z3跟踪总扰动。

为保证风力发电系统的安全性及稳定性，在变桨执行机构工作时，对叶片桨距角的大小及变化速率做出一定的限制。图1中θ0是非线性控制律计算控制量，θref是自抗扰控制器输出的桨距角，θ是经执行机构输出的叶片桨距角值。

2.1 改进的光滑非线性函数

非线性函数是ESO及NLSEF的重要组成部分，而ESO及NLSEF是自抗扰控制器的核心组成，因此对自抗扰控制器进行设计时，首先考虑到对非线性函数的设计。

目前广泛应用的非线性函数是fal(e,a,d)函数。fal(e,a,d)函数是一个分段函数，以函数的线性区间宽度d作为函数的分界点。在分界点处，fal(e,a,d)函数虽然连续但并不平滑。为了更好地系统输出性能，一般将d设置得很小，但此时函数fal(e,a,d)导数的突然变化导致系统性能变坏，系统存在一定的高频振荡问题[13]。基于以上问题，设计一个在连续光滑的非线性函数，以改善系统的抗扰动性能。

2.1.1fal(e,a,d)函数

fal(e,a,d)函数的表达式为

(7)

为观察fal(e,a,d)函数的性能，对函数做出以下仿真。

(1)令d=0.5，改变a，fal(e,a,d)函数的响应曲线如图2(a)所示。

(2)令a=0.5，改变d，fal(e,a,d)函数的响应曲线如图2(b)所示。

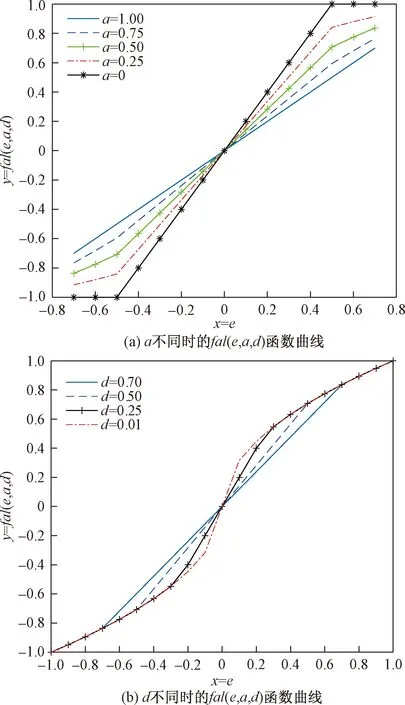
图2 fal(e,a,d)函数响应曲线Fig.2 fal(e,a,d) function response curves

从图2看出，在分界点±0.01、±0.25、±0.5、±0.7处，响应曲线出现明显的转折角，函数不是光滑可导的。比较幂函数的指数a不同时的四条函数曲线，发现a越小，函数的非线性程度越强。d决定了函数的线性区间宽度，当误差在线性区域内时，系统不会产生振荡。但是，如果d较小，在导数突然变化时，系统受到一定影响从而产生高频振荡现象。

2.1.2 改进fal(e,a,d)函数

基于fal(e,a,d)函数的曲线不平滑问题，在fal(e,a,d)函数基础上设计了一个连续光滑的非线性函数Ifal(e,a,d)函数，以改善系统的抗扰动性能。

当|e|>d时，Ifal(e,a,d)函数满足：

(8)

当|e|≤d时，Ifal(e,a,d)函数为多项式与反正弦函数的拟合形式：

Ifal(e,a,d)=me+ne2+parcsine

(9)

即Ifal(e,a,d)表达式为

(10)

式中：m、n、p分别为多项式和反正弦函数的系数。

为满足Ifal(e,a,d)函数连续和可导条件，由式(10)可得：

(11)

即:

(12)

求解式(12)，得:

(13)

因此，Ifal(e,a,d)表达式为

Ifal(e,a,d)=

(14)

为了验证Ifal(e,a,d)函数的性能，对函数做出以下仿真。

(1)令d=0.5，改变a，Ifal(e,a,d)函数的响应曲线如图3(a)所示。

(2)令a=0.5，改变d，Ifal(e,a,d)函数的响应曲线如图3(b)所示。

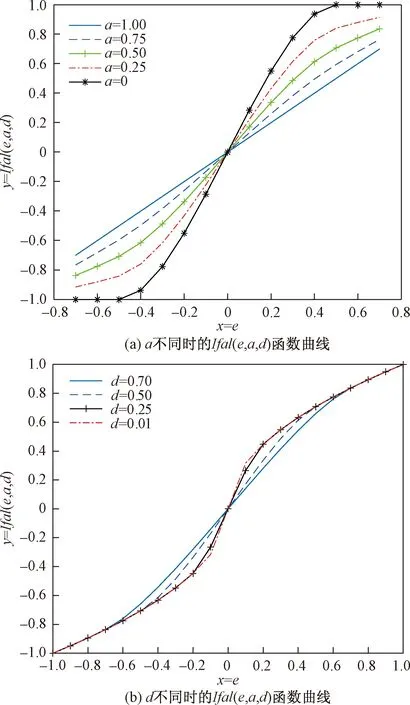
图3 Ifal(e,a,d)函数响应曲线Fig.3 Ifal(e, a, d) function response curves

从图3可知，a和d对Ifal(e,a,d)函数和fal(e,a,d)函数的影响一致。a决定Ifal(e,a,d)函数的非线性程度，d决定了Ifal(e,a,d)函数的线性区间宽度。

在函数Ifal(e,a,d)和fal(e,a,d)中，取参数a=0.5，d=0.5，所得函数的曲线如图4所示。

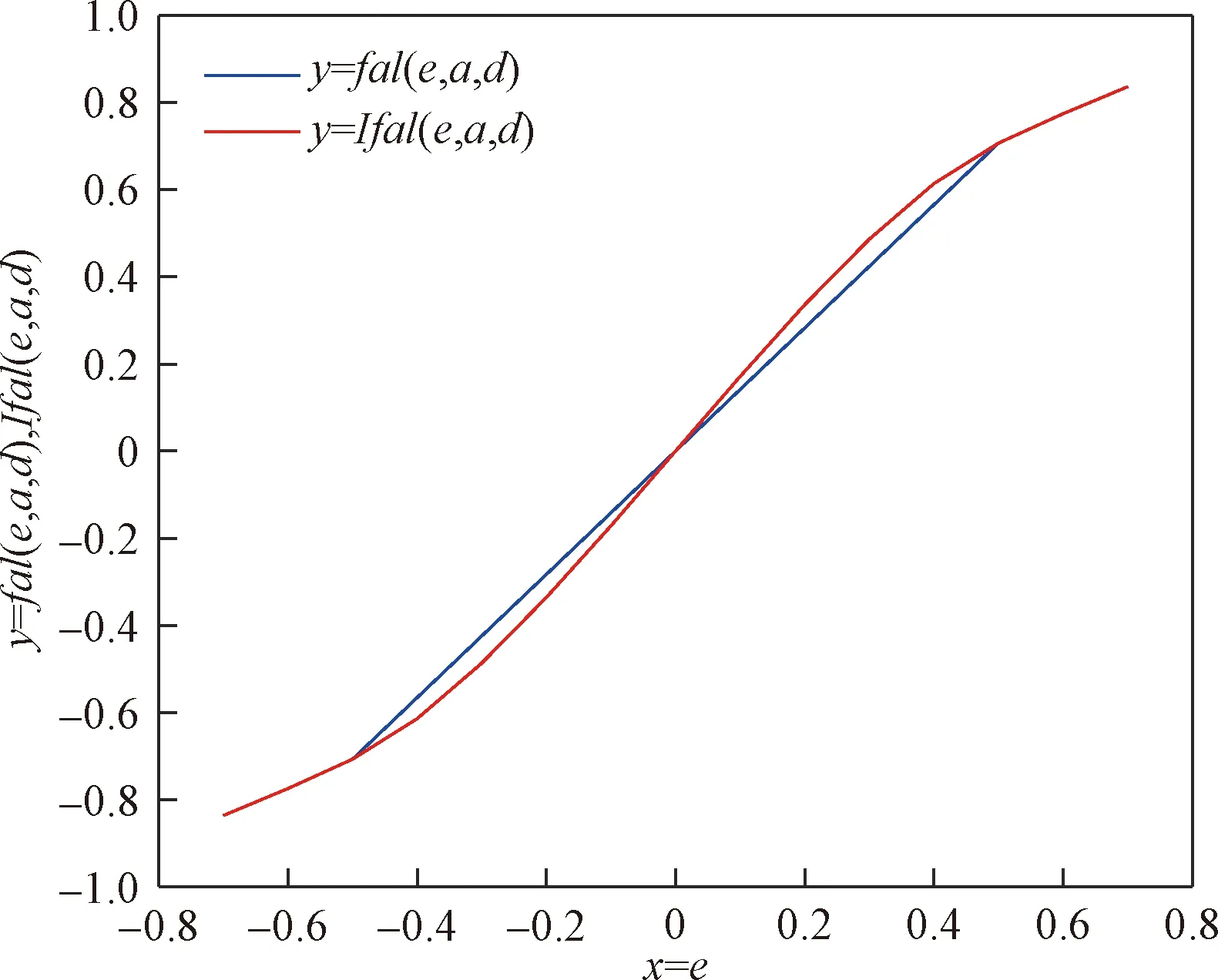
图4 函数Ifal(e,a,d)和fal(e,a,d)响应曲线Fig.4 Response curves for Ifal(e,a,d) function and fal(e,a,d) function

从图4可以看出，在分界点±0.5处，fal(e,a,d)函数有明显的转折，而改进的函数Ifal(e,a,d)在分界点能够平滑过渡。在整个区域内，Ifal(e,a,d)函数比fal(e,a,d)函数呈现出更好的平滑性。因此，在设计变桨距自抗扰控制器时，均使用Ifal(e,a,d)对ESO和NLSEF进行改进。

2.2 改进型自抗扰变桨距控制器设计

在改进型自抗扰变桨距控制器设计中，TD为系统安排了一个平缓的过渡过程。TD将输入信号转化为平滑的信号，减少系统的初始误差。

TD算法如下所示：

(15)

式(15)中：T为采样周期，r为跟踪快慢的速度因子，h为决定滤波效果的滤波因子;其中fst(·)函数的定义如下：

(16)

由式(16)可知，TD需要对r、h、T进行调整。一般来说，滤波因子h可以和控制器采样周期T取值相同。r越大跟踪速度越快，但同时会加大系统微分信号的振荡。因此，对r进行调整时，既要保证合适的跟踪速度又要选取尽量小的数值。

众所周知，系统模型与实际工业之间的偏差始终存在，此种情况影响系统的控制效果。在改进型自抗扰变桨距控制器设计中，改进型ESO对输入的非线性因素、系统建模误差及内外干扰进行观测与补偿。因此，避免了不确定干扰因素对风力发电系统的影响，改善系统的控制效果。

改进型 ESO 的算法如下所示:

(17)

Ifal(e,a,d)=

(18)

由式(17)、式(18)可知，改进ESO需要对d、b0、a1、a2、β01、β02、β03进行调整。β01、β02、β03是改进型ESO的增益，反应系统的动态性能，在改进型ESO参数整定中，最重要的是对这三个数的取值。β01、β02、β03与系统的响应速度和控制效果有关。增益越大，系统的调节时间会越小，但不能过度地调大参数值，当达到一定界限后，系统的稳定性会降低。因此，应在保障良好的跟踪效果下，对相互影响的三个参数β01、β02、β03进行协调整定。d是带宽；a1、a2为非线性因子，此三个参数一般在0～1之间进行取值；b0是补偿因子的估计值。

在改进型自抗扰变桨距控制器设计中， 将TD和改进型ESO的输出信号的偏差作为改进型NLSEF的输入信号，改进型NLSEF对输入信号进行非线性组合，同时考虑到扰动补偿输出理想的控制信号。

改进型NLSEF的算法如下所示:

(19)

式(19)中：aa1、aa2为非线性因子，一般在0～1之间进行取值；β1、β2分别是误差和误差微分的增益，β1、β2的调整与传统PID类似；如果超调量小，要适当调大β1的值；如果要提高系统的动态性能，要适当调大β2的值。

3 改进型自抗扰变桨距控制仿真与结果分析

为验证改进型自抗扰变桨距控制器的控制效果，在Simulink中搭建了一个功率为2 MW的永磁直驱风电机组的数学模型，并将传统PID控制器、ADRC及改进ADRC应用到模型中，进行仿真试验。2 MW永磁直驱风电机组的参数如表1所示。

PID控制器的参数为:kp=2.1×10-6，ki=3.18×10-6。为了保证结果的可靠性及合理性，令ADRC和改进ADRC的参数取值相同。经多次试验，改进型ADRC的参数整定结果如表2所示。

图5所示为风速测量仪测量的100 s内的大于额定风速的风速曲线。

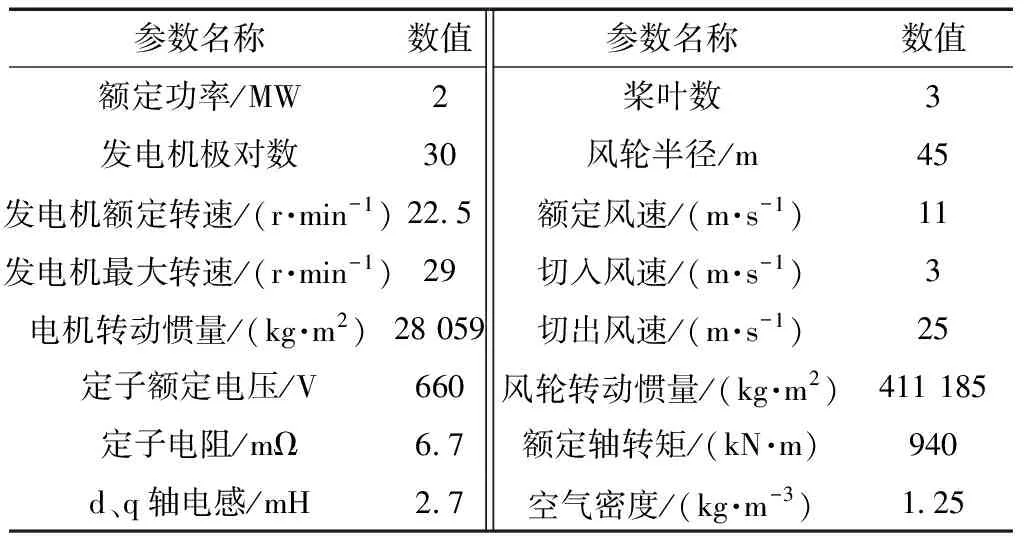
表1 2 MW永磁直驱风电机组的参数Table 1 Parameters of 2 MW permanent magnet direct drive wind turbine

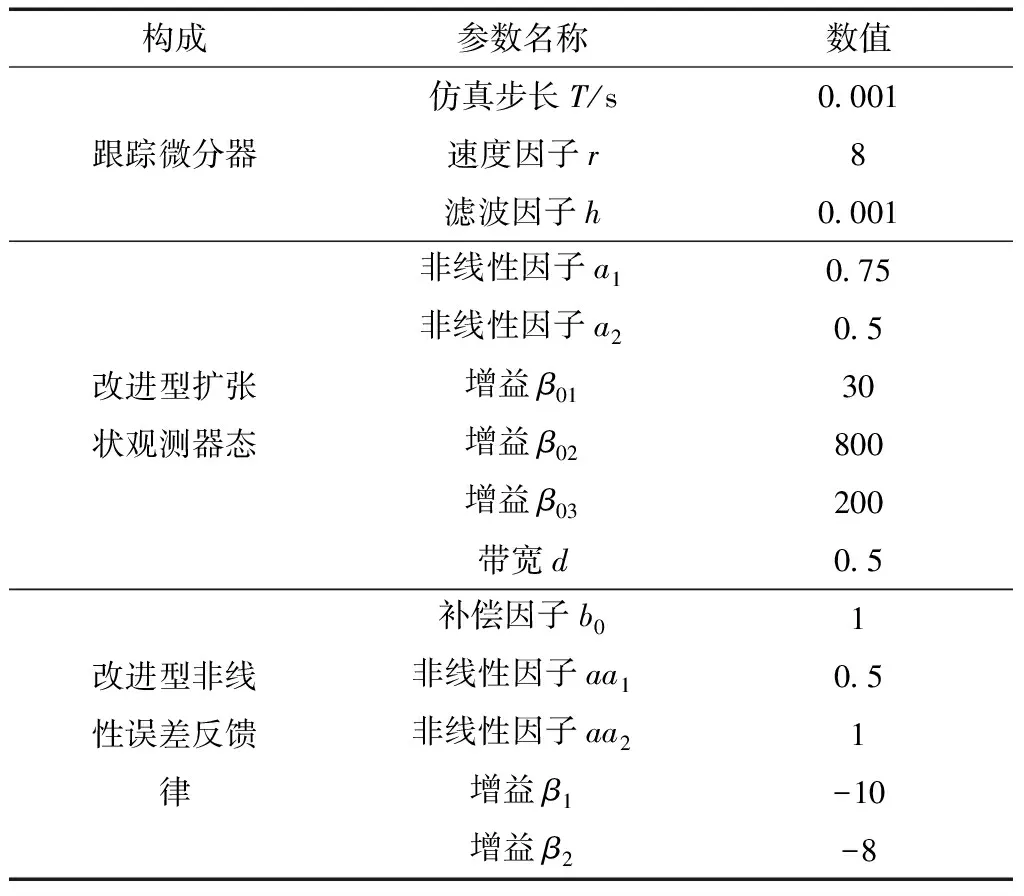
表2 改进型自抗扰控制器参数设置Table 2 Improved active disturbance rejection controller parameter settings

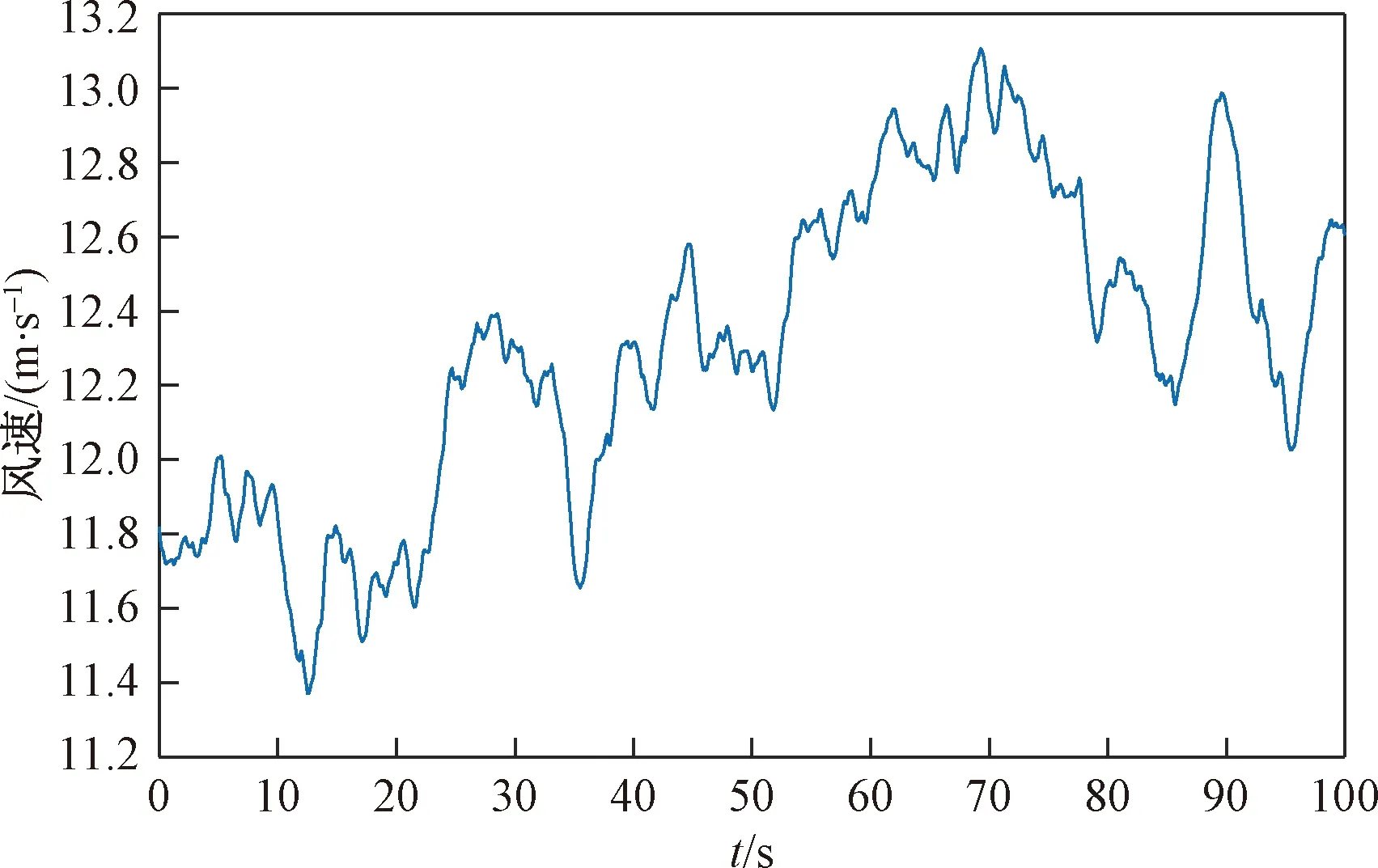
图5 100 s内大于额定风速的风速曲线Fig.5 Wind speed curve greater than rated wind speed in 100 s

将图5所示的100 s内的风速信号作为风电机组的输入信号，变桨控制器选用传统PID、ADRC和改进ADRC，仿真结果如图6～图9所示。

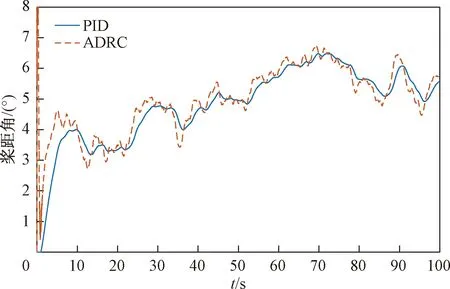
图6 PID与ADRC控制桨距角对比Fig.6 Comparison of pitch angle control between PID and ADRC

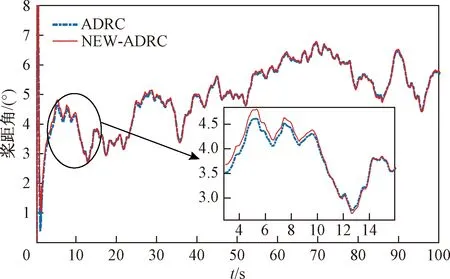
图7 ADRC及改进型ADRC控制桨距角对比Fig.7 Comparison of pitch angle control between ADRC and improved ADRC

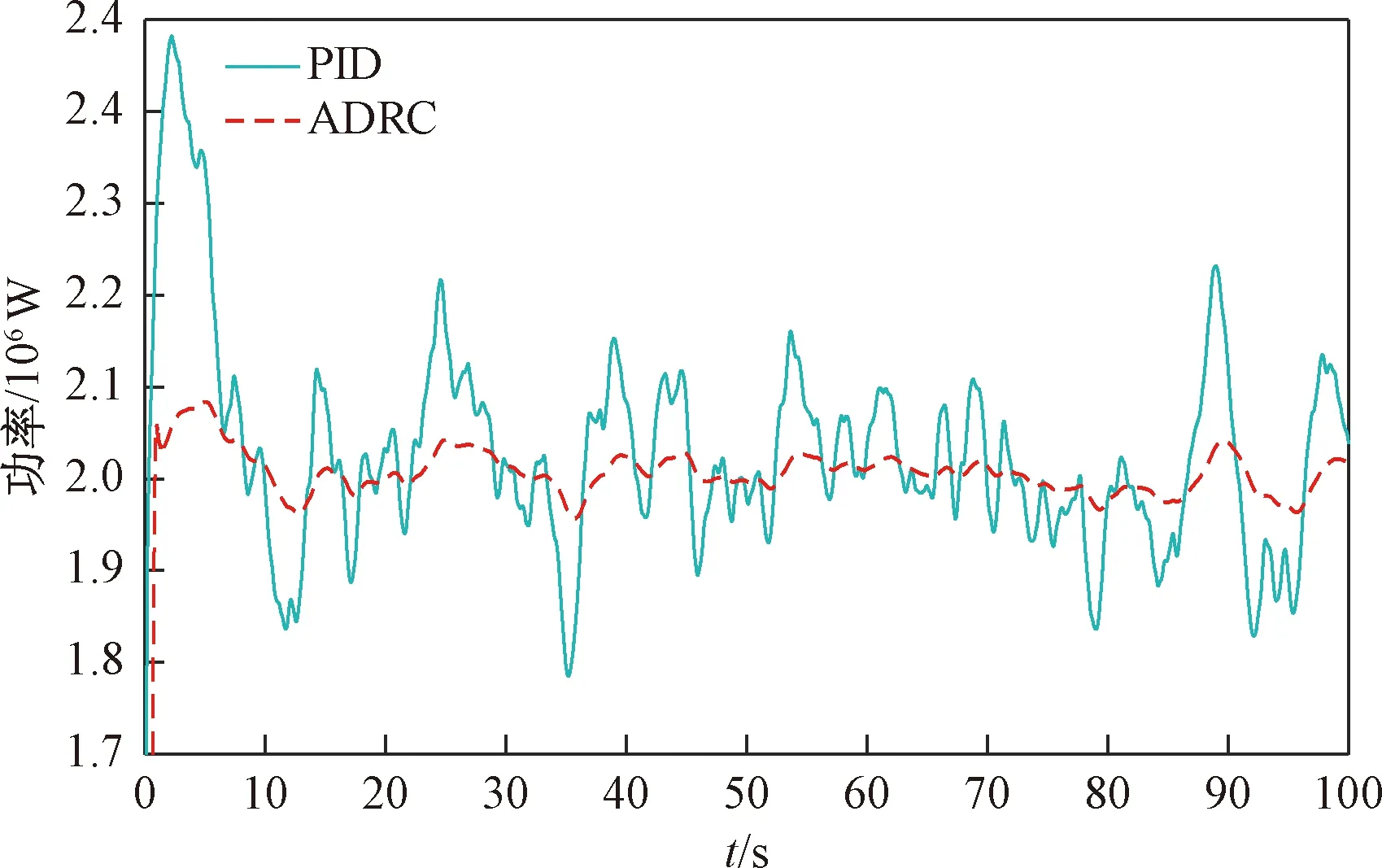
图8 PID控制器与ADRC输出功率对比Fig.8 Comparison of output power between PID controller and ADRC

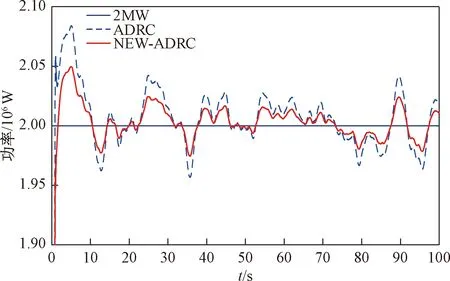
图9 ADRC与改进ADRC输出功率对比Fig.9 Comparison of output power between ADRC and improved ADRC

图6所示为PID与ADRC控制的输出桨距角变化对比。第21.6 s时风速突然上升，ADRC控制下的桨距角在第22 s迅速反应并增大桨距角，PID控制下的桨距角在第23 s时做出响应并增大桨距角，且桨距角变化幅度较ADRC控制来说较小；第33.1 s时风速突然下降，ADRC控制下的桨距角在第33.3 s迅速反应并减小桨距角，PID控制下的桨距角在第34 s时做出响应并减小桨距角，且桨距角变化幅度较ADRC控制来说较小。当风速大于额定风速时，对比两种控制下的桨距角响应曲线，清晰得出: 当风速发生变化时，无论从桨距角的响应时间还是响应幅度来看，ADRC控制效果都优于PID控制。

图7所示为ADRC与改进ADRC控制的输出桨距角变化对比。ADRC与改进ADRC控制的桨距角都能快速响应风速变化，整体来看，两种控制输出的桨距角略有区别。观察3～16 s的输出桨距角响应曲线的放大图，清晰看出改进ADRC控制的桨距角的灵敏度稍优于ADRC。高风速时，风轮的气动转矩对桨距角的灵敏度也比较高。因此，当风速大于额定风速时，桨距角的细微变化对风力发电系统有较大的影响。

图8所示为PID与ADRC控制的风电机组的输出功率对比。由响应曲线可以看出，PID与ADRC控制都可将输出功率稳定在2 MW附近，但相对于PID控制器，ADRC控制器输出的功率响应曲线幅值波动比较小，且稳定速度更快。因此，ADRC对风电机组的控制性能远优于PID控制。

图9所示为ADRC与改进ADRC控制的风电机组的输出功率对比。整体来看，两种控制下的输出功率响应曲线十分相似，都可在短时间内将风电机组输出功率维持在2 MW附近。从图9中可知，虽然两种控制下的输出功率略有差异，但在第5、12、25 s等时刻，功率误差也达到20 kW左右。当风机并网后，20 kW的波动对电网的稳定性及安全性产生一定的影响。因此，改进型ADRC风机变桨距控制有较好的输出性能，提高了系统的稳定性。

4 结论

首先阐述了自抗扰控制技术的控制原理，之后为改善风电机组的恒功率输出区域的动态性能，提出了一种改进ADRC的风机变桨距控制策略。考虑到传统非线性函数在分界点处不平滑而导致的系统不稳定问题而设计一个连续光滑的非线性函数来改善系统的抗扰动性能。为验证改进型自抗扰变桨距控制器的控制效果，在MATLAB/Simulink中搭建了一个功率为2 MW的永磁直驱风电机组的数学模型，并将传统PID控制器、ADRC及改进ADRC应用到模型中，进行仿真试验。根据仿真试验，得到如下结论。

(1) 改进的非线性函数Ifal(e,a,d)比fal(e,a,d)函数呈现出更好的平滑性，且在分界点处能够平滑过渡，拥有更好的输出性能。

(2) 改进ADRC的变桨距控制系统有灵敏的桨距角变化，可以将输出功率快速稳定到额定值附近，有效缩短了系统调节时间，提高了系统的响应特性及抗扰动性能。