基于Penman-Monteith模型的低丘红壤区稻田蒸散模拟∗
文建川,景元书**,韩丽娟
(1.南京信息工程大学气象灾害预报预警与评估协同创新中心/应用气象学院,南京 210044;2.国家气象中心,北京 100081)
生态系统中植被发育以及系统生产力都受到蒸散的直接影响,同时它不仅是土壤-植被-大气连续体中水分传输中的重要环节,也是生态系统中能量平衡的主要组成部分[1]。据统计,以蒸散的形式消耗农业用水占到90%[2-3],蒸散的准确估算有利于作物水分生产力提升以及改善农田或流域灌溉管理[4-5],因此,蒸散观测和模拟一直受到生态气象领域学者的广泛关注。
近几十年来,蒸散估算模型众多,在该研究领域较为有名的是以能量平衡和微气候学方法为原理的Penman-Monteith模型(简称PM模型),该模型模拟精度主要取决于冠层阻力这一关键性参数[7]。国内外研究者基于冠层阻力公式,对其与PM模型结合后模拟蒸散量开展了不少研究。Irmak 采用非线性回归方法设计了7个形式相同,气象因子数量不同导致复杂程度不一样的模型,之后利用该模型对大豆蒸散量进行模拟,取得了较好的结果[8-9]。吴林等[10]将Irmak 公式应用到PM模型中,可以很好地估算黑河绿洲区玉米半小时尺度上的蒸散量。赵华等[11]采用Jarvis 公式计算了南京地区2012年和2013年水稻拔节-成熟期的冠层阻力,并将其耦合到PM模型中模拟水稻该时期的蒸散,两年的拟合度都超过0.95。Li 等[12]采用PM_Jarvis模型时,基于玉米叶面积指数大小将整个生育期划分为两个阶段,分段拟合模型中的经验系数,对比后发现以叶面积指数为0.5 分段拟合的系数进行蒸散模拟的效果最佳。Srivastava等[13]比较了Monteith、Katerji-Perrier、Todorovic和Jarvis 四种冠层阻力公式应用在PM模型中的模拟效果,结果表明Jarvis和Todorovic 都较好地估算了半湿润地区玉米的蒸散。Jarvis和Irmak 公式中包含了较多经验系数,有学者分别将其它研究的经验系数值和通过非线性拟合得到的系数值代入到模型中估算蒸散量,比较后发现借用其它研究的经验系数得到的模拟值与实测值相关性较差[14]。
因为不同地区气候差异大,这两种模型同属为经验模型,Jarvis和Irmak 公式应用在PM模型中估算蒸散量,能否取得较高的模拟精度,是否适用于低丘红壤区稻田蒸散研究,有待进一步探索。因此,需要针对试验区及作物,挑选出最为合适的冠层阻力公式,得到模拟精度高的蒸散模型。另外,Jarvis模型中各胁迫函数存在多种表达式,导致有多种组合形式,较多学者在使用该模型时,基本上都是选取其中一种组合形式进行模拟,但是不同的表达式所涉及的参数数量不同,可能导致最后的模拟精度有差别。赵华[15]采用了Jarvis模型中的几种组合形式,对冬小麦和水稻蒸散量进行研究,但只选取了各生育期中典型晴天数据,未对作物全生育期进行验证。因此,本研究以波文比仪监测该地区稻田的蒸散量作为实测值,对比分析PM_Jarvis1-8(胁迫函数的8种组合形式)与PM_Irmak 共9个模型的蒸散模拟效果,旨在选出更适用于低丘红壤区稻田的实际蒸散模型,准确估算蒸散量,以利于制定更合理的灌溉计划和提高稻田的水分利用效率。
1 材料与方法
1.1 试验站点概况
试验站点位于江西省鹰潭市中国科学院红壤生态试验站(116°55'E,28°15'N),该站地处武夷山至潘阳湖平原的过渡地带鹰潭盆地,属亚热带湿润季风气候,年平均气温17.6℃,降水量1788.8mm,日照时数1739.4h。试验观测时间为2014年和2015年晚稻生长季(7-10月),水稻移栽后,依照当地大田生产进行田间管理。观察期内水稻生育期见表1。
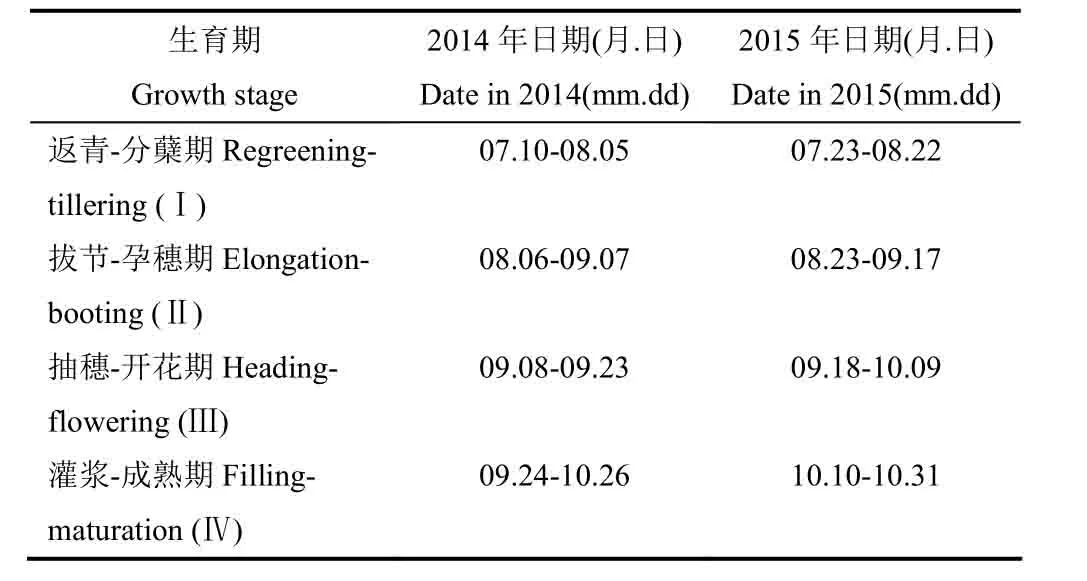
表1 试验区2014年和2015年水稻生育期Table1 Growth stage of rice in experimental area in 2014 and 2015
1.2 数据来源
波文比仪架设在稻田中部,该系统由NR-Lite净辐射传感器(Kipp&Zonen,Netherland)、两层空气温湿度传感器( HMP155A)、CR1000 数据采集器、风速仪( 010C-1)组成,自动采集1.5m 高度差之间的温湿度差,计算得到波文比值。土壤热通量由埋深为 5cm的土壤热通量板(Hukseflux,HFP01,Netherland)测得。气象数据由布设在农田中部的自动气象站(HOBO U30,ONSET,USA)监测,观测内容包括相对湿度、气温、2m 风速、气压等小气候数据,观测频率为20min。
1.3 数据处理方法
波文比测定水热通量是以地表能量平衡方程为依据,即

式中,Rn 为净辐射通量(W·m-2),λET 为潜热通量(W·m-2),H 为感热通量(W·m-2),G 为土壤热通量(W·m-2)。其中,Rn和G可以实测得到,λET和H 通过计算得到。
波文比(β)为感热通量和潜热通量的比值,根据莫宁-奥布霍夫理论,假定水汽和热量的湍流扩散系数Kh与Kw相等,则有

式中,γ 为干湿表常数,取值为0.067kPa·℃;ΔT、Δe 分别为波文比系统的两层观测高度的温度差和水汽压差。
波文比仪测定出两层高度的温度差和水汽压差、净辐射通量以及土壤热通量板测定的土壤热通量数据,结合式(1)和式(2),可得潜热通量λET 为

式中,λ 为水的汽化潜热,取值为2.45MJ·kg-1,ET 为蒸散量(mm)。
因为日出、日落以及降水天气,可能造成误差,所以根据Perez 等[16]提供的方法确定无效β 值,将其剔除并进行插补。计算式为
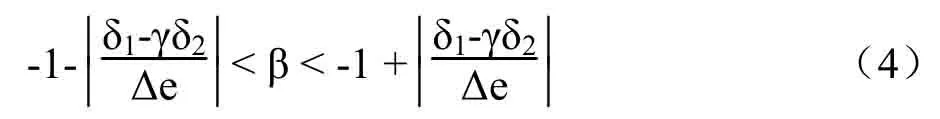
式中,δ1和δ2分别为温、湿度传感器的测量精度。
1.4 模型介绍
1.4.1 冠层阻力计算模型
冠层阻力rc,采用两种模型进行计算。
(1)PM_Jarvis模型
Jarvis 认为冠层阻力与环境因子具有协同关系,而且不同环境因子对冠层阻力的影响独立,因此,提出了冠层阻力与环境因子之间的关系式,即
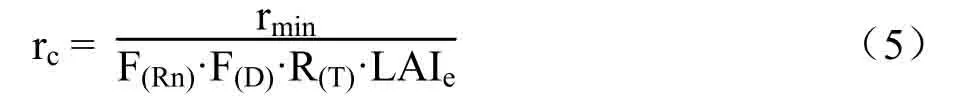
式中,rmin为最小冠层阻力,根据前人[17]研究结果,水稻在拔节期、孕穗期、抽穗期、乳熟期的rmin分别取为40、45、50、60s·m-1,LAIe为有效叶面积指数,F(Rn)、F(D)、F(T)分别为太阳辐射胁迫函数、饱和水汽压差胁迫函数、温度胁迫函数,因以上3种胁迫函数均有多种表达式,导致存在不同组合形式,不同的表达形式有可能影响模拟精度,因此,每个胁迫函数均选取其中两种表达式。
有效叶面积指数LAIe为[18]
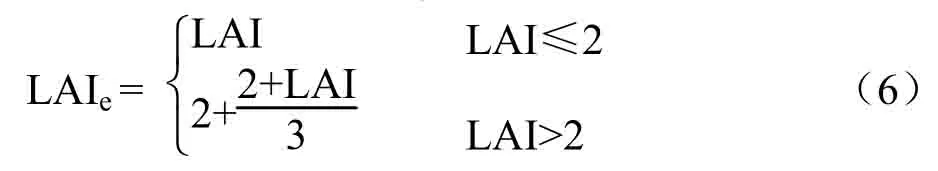
太阳辐射胁迫函数分别采用线性关系式[19]和指数关系式[12],即

饱和水汽压差胁迫函数分别采用双曲线关系式[19]和线性关系式[12],即

空气温度胁迫函数分别采用以下两种关系式[12,19],即

式中,Rn为净辐射通量(W·m-2),D 为饱和水汽压差(kPa),T 为空气温度(℃),a1、a2、a3、a4、b1、b2、b3、c1、c2、c3、c4为模型经验系数。
基于上述各胁迫函数的响应表达式,得到8种不同的Jarvis模型组合形式(表2)。
(2)PM_Irmak模型
Irmak 等采用广义非线性回归方法,构建了关于气象因子、叶面积指数与空气动力学阻力的冠层阻力模型,即
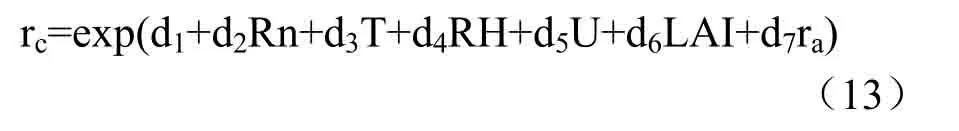
式中,rc为冠层阻力(s·m-1),Rn 为净辐射(W·m-2),T 为空气温度(℃),RH 为相对湿度,U 为风速(m·s-1),LAI 为叶面积指数,ra为空气动力学阻力(s·m-1),按Rana 等提出的公式计算[20],即

表2 PM_Jarvis 冠层阻力模型中3种胁迫函数表达式的不同组合Table2 Different combinations of three stress function expressions of the PM_Jarvis canopy resistance model
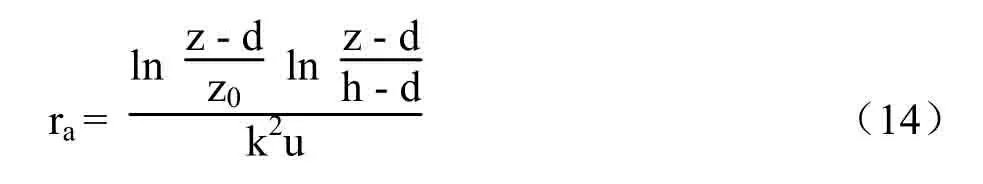
式中,z 为参考高度(m),取值为1.5m;h 为冠层高度(m),以实测株高代替;k 为Von Karman常数,取值为0.41;u 为风速(m·s-1),z0=0.13h,d=0.63h。
1.4.2 蒸散量计算模型
Monteith 在Penman 基础上,引入了空气动力学阻力和冠层阻力等参数,提出以能量平衡和水汽扩散理论为基础的适用于作物蒸腾计算的阻力模式,即Penman-Monteith模型。
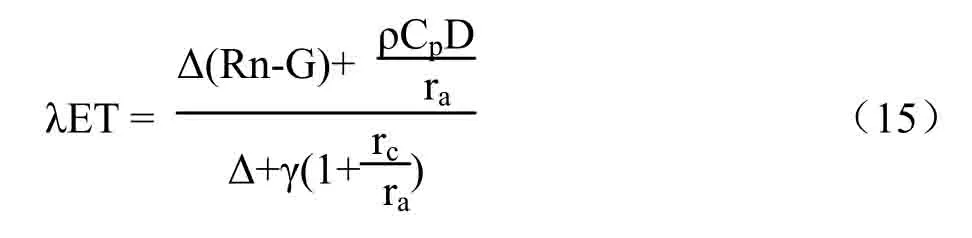
式中,λET 为潜热通量(W·m-2);Rn 为净辐射通量(W·m-2);G 为土壤热通量(W·m-2);Δ 为饱和水汽压曲线斜率(kPa·K-1);ρ 为空气密度,取值为 1.29kg·m-3;Cp 为空气定压比热,取值为1004J·kg-1·K-1;D 为饱和水汽压差(kPa);γ 为干湿表常数,取值为0.067kPa·K-1;rc为冠层阻力(s·m-1);ra为空气动力学阻力(s·m-1)。
1.5 模型精度分析
以波文比仪测定的蒸散量ET 作为参照,分别把不同冠层阻力模型应用到Penman-Monteith 公式中,再将模拟得到的ET 与实测值比较。模型的模拟精度评价指标包括均方根误差(RMSE)、平均绝对误差(MAE)、纳什效率系数(NSE)和一致性指数(IA)、确定系数(R2)。
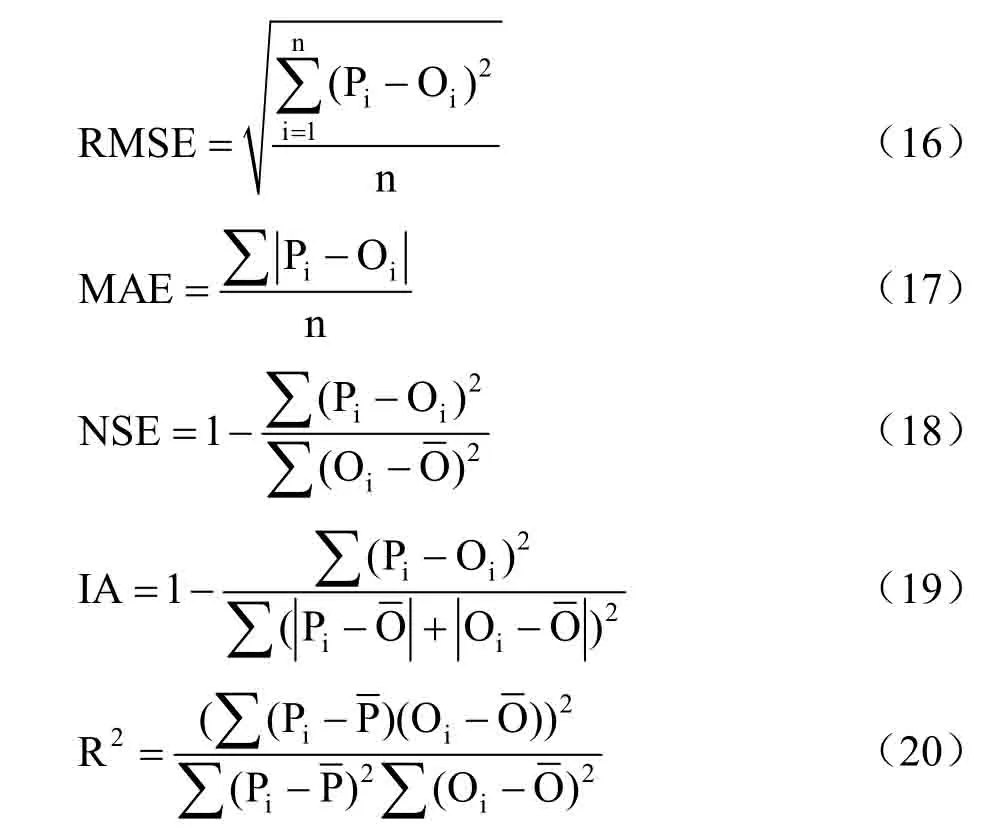
式中,Pi为模拟蒸散量(mm·h-1),Oi为实测蒸散量(mm·h-1),为实测蒸散量的平均值(mm·h-1),为模拟蒸散量的平均值(mm·h-1),n 为个数。
RMSE和MAE 反映模拟值与实测值之间的差异,数值越接近0,表明误差越小;NSE 越接近1,表明模型可信度越高;IA 反映模拟值与实测值的符合程度,数值越接近1,说明模型的预测效果越好。R2越接近1,表明拟合程度越好。
2 结果与分析
2.1 PM_Jarvis和PM_Irmak 冠层阻力模型模拟效果
基于2014年波文比仪监测的水稻全生育期实测蒸散量与同阶段的气象数据,将表2中组合好的8种Jarvis模型及Irmak模型分别与Penman-Monteith模型结合,简称PM_Jarvis1-8模型(胁迫函数8种组合形式)、PM_Irmak模型,利用1stOpt 软件进行非线性拟合(http: //www.7d-soft.com/en/),通过全局优化算法,得到各模型的经验系数值(表3)。统计这9种蒸散模型的误差及相关性统计参量,结果见表4。从表4中可知,不同组合形式的PM_Jarvis模型精度指标都存在一定的差异,其中PM_Jarvis6模型精度最低,其RMSE、MAE 最高,NSE、IA 及R2最低。PM_Irmak模型的RMSE、MAE 在9种模型中最低,NSE、IA 及R2较其余模型更接近1,表明该模型模拟精度最高。就PM_Jarvis模型而言,8种组合形式模型的模拟精度存在差别,将模型进行两两对比,结果表明,对于太阳辐射胁迫函数,F1(Rn)的表达式在应用于该模型中较F2(Rn)效果更佳;对于饱和水汽压差胁迫函数和空气温度胁迫函数,F1(D)、F1(T)的表达式分别优于F2(D)和F2(T)。
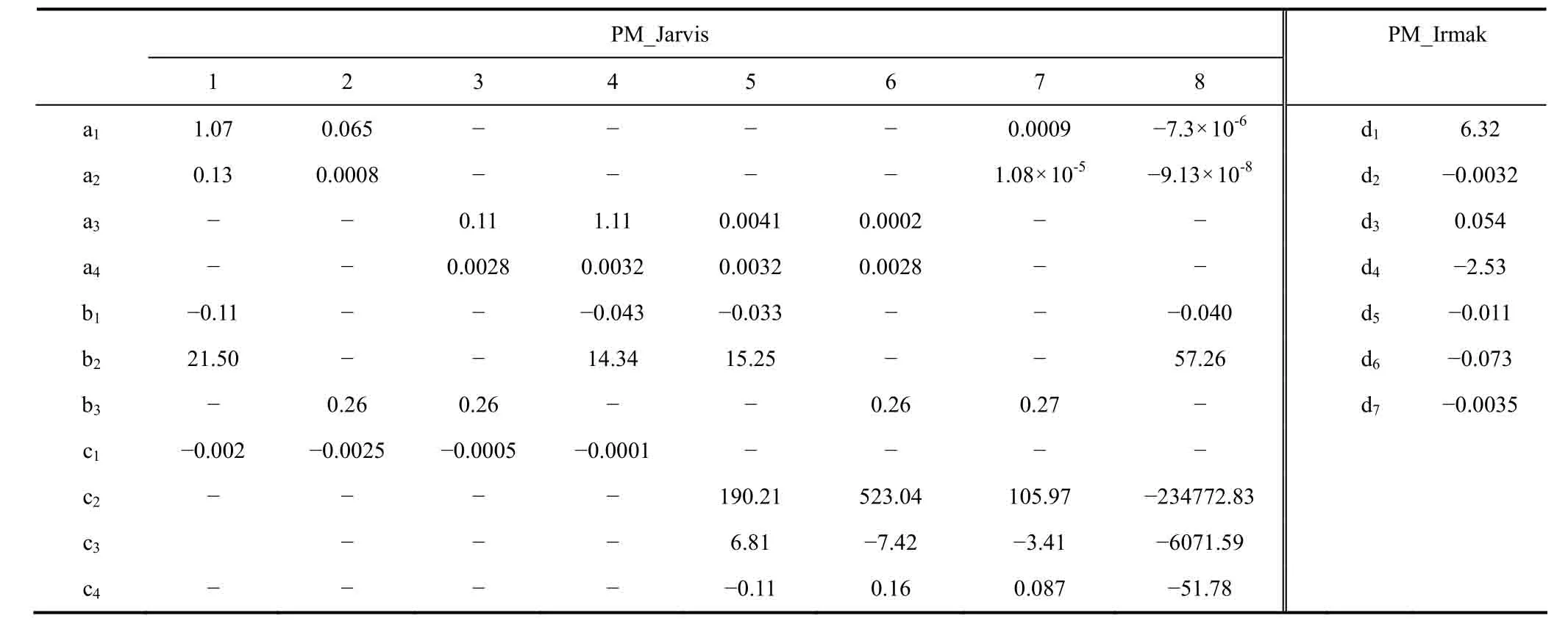
表3 PM_Jarvis(式7-12)和PM_Irmak(式13)模型中各参数的拟合值Table3 Simulation value of parameters in PM_Jarvis(Equation7-12) and PM_Irmak models(Equation13)
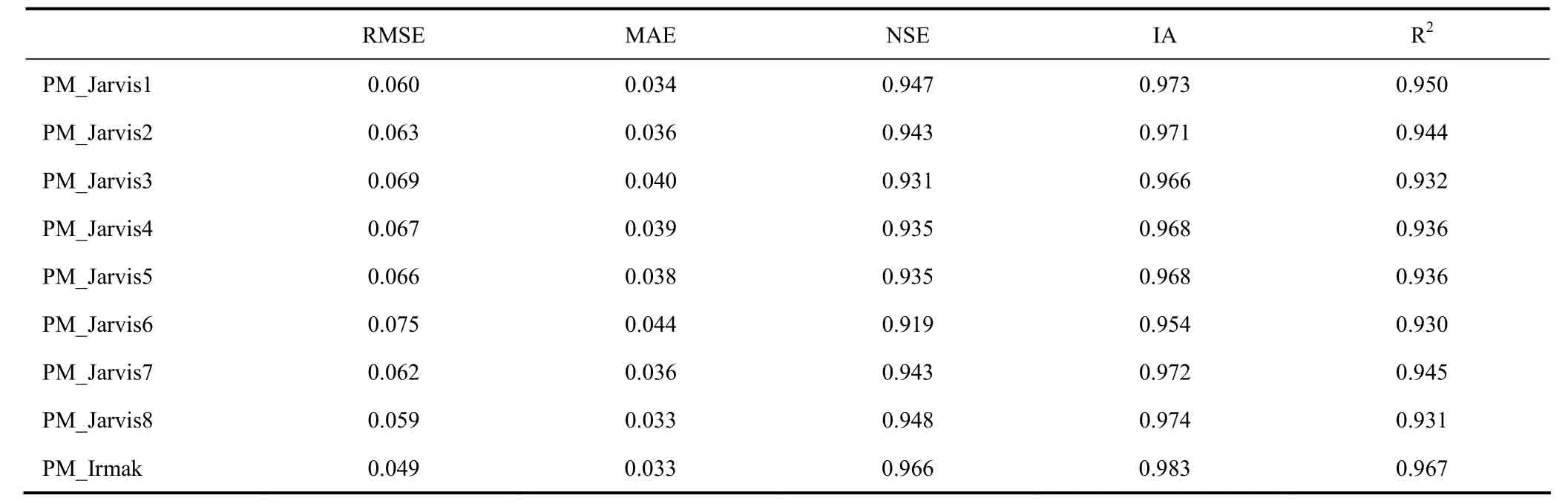
表4 PM_Jarvis和PM_Irmak 模拟2014年逐时蒸散的统计参量Table4 Statistical parameters of hourly evapotranspiration simulated by PM _Jarvis and PM_Irmak models
2.2 PM_Jarvis和PM_Irmak 模拟结果验证
利用2015年7月23日-10月31日的气象资料和水稻生理数据,代入9种模型计算蒸散量,并与波文比仪监测的该时段蒸散量比较,进一步验证模型。从图1看出,PM_Irmak模型模拟的蒸散量与实测蒸散量基本沿1:1 线分布,且散点集中,表明模拟值与实测值较接近;其余8种PM_Jarvis模型散点大都位于1:1 线下方,总体上表现出偏低趋势。为了更全面地体现模型模拟效果,在全生育期及各生育阶段进行精度分析,结果见表5和图2。由表5可以看出,PM_Irmak模型在估算水稻全生育期蒸散量中,各评价指标整体均优于其余模型,同样,就PM_Jarvis模型而言,胁迫函数表达式不同导致8种PM_Jarvis模型精度不一,与2014年结果一致。
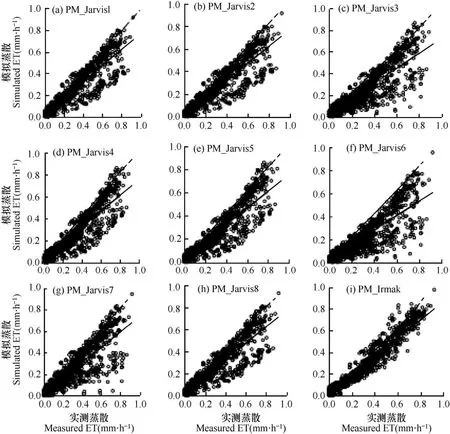
图1 PM-Jarvis和PM-Irmak模型模拟逐时蒸散量与实测蒸散量对比Fig.1 Comparison of hourly evapotranspiration( ET) between measured and simulated by PM-Jarvis and PM-Irmak models
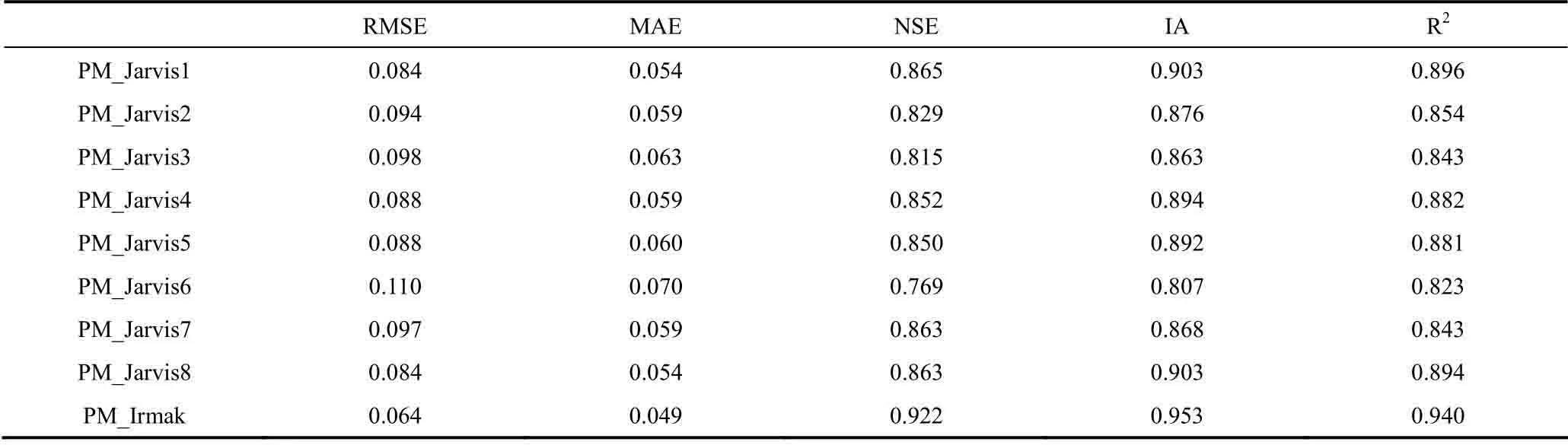
表5 PM-Jarvis和PM-Irmak模型模拟的稻田全生育期蒸散量精度验证(2015年)Table5 Accuracy of evapotranspiration during the whole growth stage of rice paddy simulated by PM-Jarvis and PM-Irmak models (2015)
将水稻的全生育期分为4个阶段,由图2可见,8个PM_Jarvis模型的4个评价指标在返青-分蘖期与后 3个生育期有明显差距,在该生育阶段,PM_Irmak模型的均方根误差(RMSE)和平均绝对误差(MAE)显著低于8个PM_Jarvis模型,纳什效率系数(NSE)和一致性指数(IA)明显较高;在后3个生育时期,PM_Irmak模型的RMSE和MAE虽然不是最低,NSE和IA 也不是最高,但与其余模型差距较小。所以认为,PM_Irmak模型总体上对水稻整个生长阶段蒸散量的模拟效果较好。
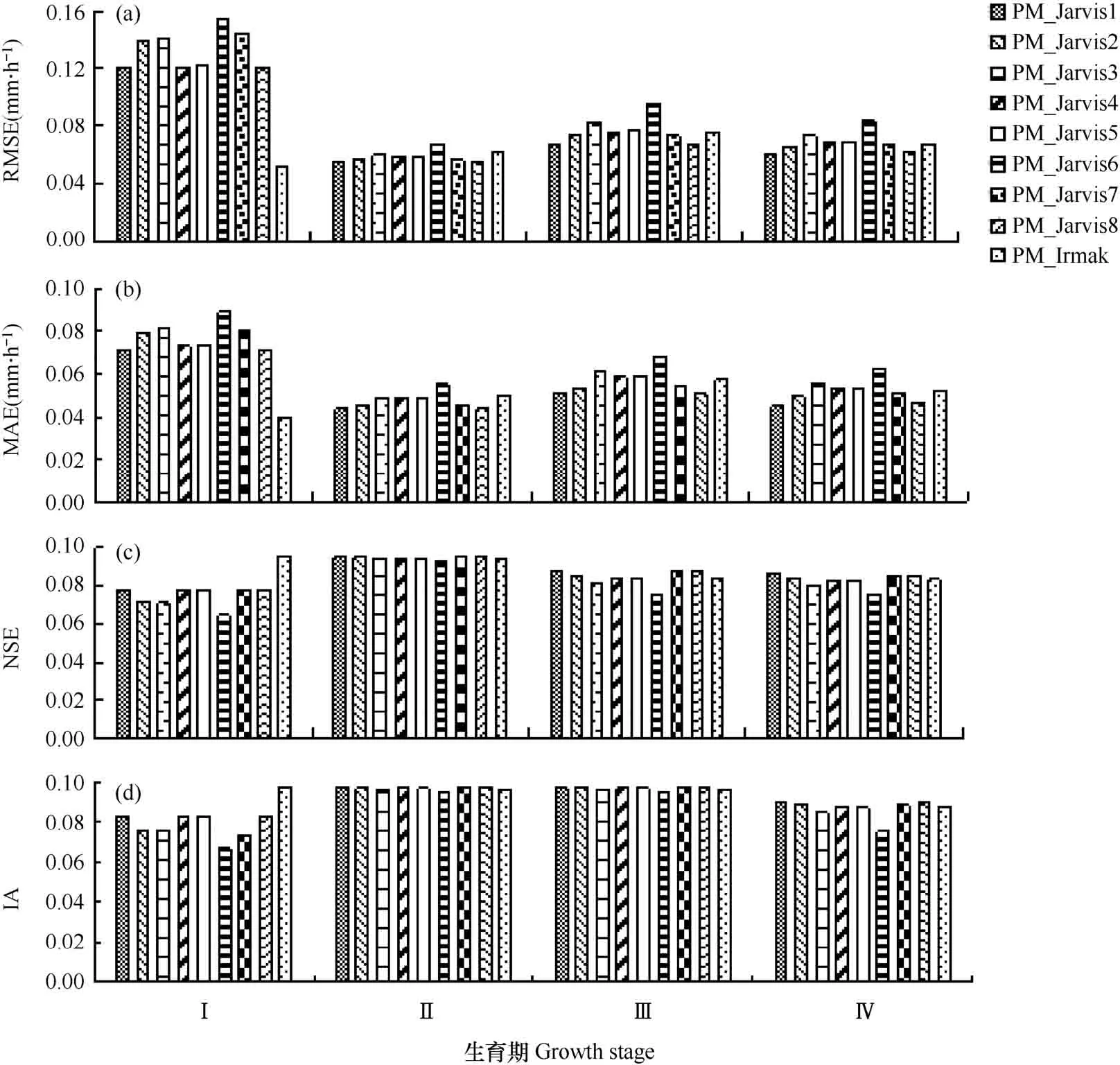
图2 PM-Jarvis和PM-Irmak模型模拟的稻田不同生育期蒸散量精度验证Fig.2 Accuracy of evapotranspiration in the different growth stages of rice paddy simulated by PM-Jarvis and PM-Irmak models
2.3 PM-Jarvis和PM-Irmak模型模拟蒸散量的日动态变化
在水稻4个生育时期中,每一阶段均选择连续9d 用来观察9个模型估算的蒸散与实测蒸散的日变化,结果见图3(下页)。由图可以看出,在返青-分蘖期(7月23-31日),PM_Jarvis1-8模型呈现出低估现象,并且低估程度严重,蒸散估算值不及实际蒸散量的50%;而PM_Irmak模型在该生育时期,除了在个别时间点(7月27日)蒸散模拟值稍偏高,其余时段均与实测值较接近,模拟效果明显优于PM_Jarvis1-8模型。在后3个生育时期,各模型模拟的日变化动态趋势同步,数值上存在差异,但差异不大,均与实测蒸散的日动态曲线基本吻合。总的来说,PM_Irmak模型在水稻整个生长阶段都能较好地估算蒸散量,所以更适用于红壤地区稻田蒸散量模拟。
3 结论与讨论
3.1 结论
本研究利用不同冠层阻力公式的PM模型估算蒸散量,与波文比仪监测的实测蒸散量对比,PM_Jarvis 1-8和PM_Irmak 共9种模型中,PM_Irmak模型的均方根误差、平均绝对误差比8种PM_Jarvis模型的均偏小,确定系数、纳什效率系数和一致性指数相比更接近 1,整体模拟效果最好。8种PM_Jarvis模型在水稻返青分蘖期的初始阶段存在明显低估现象,而PM_Irmak模型在水稻所有生育阶段的模拟值均与蒸散日变化动态值接近。
3.2 讨论
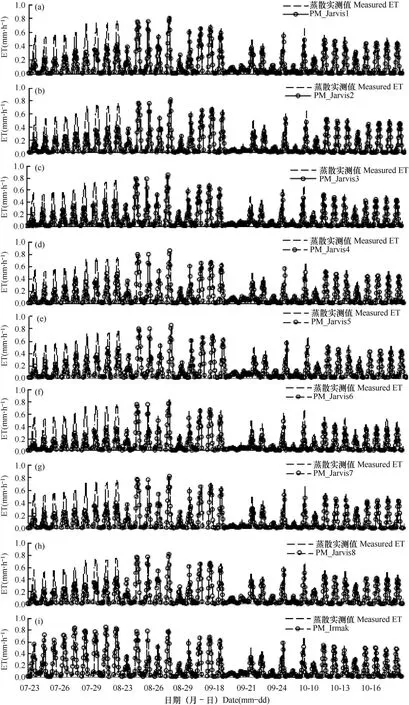
图3 PM_Jarvis和PM_Irmak模型模拟值与实测值的蒸散日变化动态Fig.3 Daily variation of observed and simulated evapotranspiration by PM_Jarvis and PM_Irmak models
因Jarvis 公式胁迫函数表达式不止一种,本研究每个函数各选取两种,组成了8种组合形式,发现PM_Jarvis1-8 模拟效果存在不同程度的差异,其中PM_Jarvis6模型(3个胁迫函数分别采用F2(Rn)、F2(D)、 F2(T)的表达式)精度最低。虽然这8种模型为同一形式,但胁迫函数的表达式不同,对最后蒸散量的模拟产生了较大影响。赵华[15]在进行水稻和冬小麦蒸散量研究时,也将不同组合形式的Jarvis 公式应用到PM模型中,发现不同模型的均方根误差和拟合度相差较大。8种PM_Jarvis模型,在返青期均呈现出明显低于实测蒸散的现象。Li 等[21]在利用PM_Jarvis模型对葡萄园蒸散进行模拟研究时,同样指出在葡萄生长前期阶段模拟蒸散也明显低于实测值,随着葡萄逐渐生长发育,二者的差异在减小,拟合效果才得以提高。因为Jarvis 把每个环境变量对作物气孔产生的影响假定为一种相互独立的行为,并认为作物所有叶片的气孔开闭都同时具有一致性,基于这样一种假设提出了该模型[22],但实际上环境变量之间存在着互相影响的关系,并且较为复杂,所以这有可能导致了该模型在作物部分生育阶段蒸散模拟效果较差。
PM_Irmak模型在返青-分蘖期各评价指标明显优于8种PM_Jarvis模型,后3个生育时期该评价指标虽不是最优,但9种模型之间差异较小,所以最终 PM_Irmak模型仍在水稻全生育期中较 8种PM_Jarvis模型有更好的模拟效果。Li 等在研究干旱地区玉米蒸散中发现,PM_Irmak模型在玉米叶面积指数小于2的时期模拟蒸散量的误差要小于叶面积指数大于2的时期,虽然在LAI 大于2时期中模型的精度略低于该研究中的其它冠层阻力模型,但是就整个生育期而言,PM_Irmak模型的均方根误差和平均相对误差都明显要小[23],这与本研究结果一致。PM_Irmak模型在水稻4个生育阶段估算的蒸散量与实测值的日变化动态均较为吻合且数值接近,精度总体来说较高,说明该模型适用于本试验区,能够更好地模拟蒸散量。

