基于Kane方程的并联平台建模方法

齐嘉兴，赵修平

(海军航空大学，山东 烟台 264001)

并联机构由于具有控制精度高、工作空间小、负载能力强等特点，目前已经得到了广泛的研究和应用[1]。为了实现对并联机构基于模型的高精度控制，对其进行动力学分析并建立准确的动力学模型是十分必要的。针对六自由度并联平台动力学方程的建立，常用的方法包括Lagrange公式[2-3]、Newton-Euler方程[4]、虚功方程[5]、Kane方程[6-13]等，很多学者通过建模分析表明Kane方程较其他方法具有高效性和简洁性。

按照Kane方程中偏速度和偏角速度的不同表述形式，可以将Kane方程的建模过程分为两种：一种是严格按照Kane方程的定义逐个求取相对于广义速率的广义主动力分量和广义惯性力分量，文献[8,11]按照这种方式给出了Kane方程建模的详细过程，但整个过程较为繁琐；另一种是通过刚体之间速度的映射关系求取每个刚体上主动力和惯性力对应的广义主动力和广义惯性力，文献[6]利用Kane方程，通过影响系数矩阵建立了并联机床的动力学模型，文献[2,7,9-10,12]利用Kane方程，通过计算各速度之间的映射关系建立了六自由度并联平台的动力学方程，使其具有更简洁的表达形式。

欧拉角和四元数被广泛用于描述动平台的姿态，当选取动平台的六维空间速度分量作为广义速率时，欧拉角、四元数与动平台空间角速度之间不具有简单地微分关系，因此需要额外的转换过程[10]。

此外，不同文献对动平台和连杆转动惯性力的计算也有不同的表述。文献[6-7]没有对运动过程中动平台和连杆惯性矩阵的计算做出明确说明；文献[9-10]利用Lagrange公式对连杆的转动惯性力进行了计算，推导过程较为繁琐；文献[8,11]将动平台和连杆对质心的惯性矩阵等价为对下平台原点的惯性矩阵。

本文使用螺旋坐标描述动平台空间姿态，以动平台的六维空间速度分量作为广义速率，通过速度之间的映射关系，求取各刚体上主动力和惯性力对应的广义主动力和广义惯性力，并给出了明确的计算过程，根据Kane方程建立了六自由度并联平台的动力学模型。

1 Kane方程

六自由度并联平台系统是包括上、下平台以及六组上、下连杆共14个刚体的刚体系，刚体系的Kane方程可以表示为[14]：

(1)

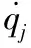
(2)

(3)

根据Kane方程建立刚体系动力学方程的过程包括：1)根据自由度数确定广义速率；2)根据广义速率，确定各刚体的偏速度和偏角速度；3)结合各刚体所受主动力、惯性力计算广义主动力和广义惯性力；4)按照Kane方程建立动力学方程。

2 并联平台速度及加速度分析

2.1 坐标系建立和参数设定

六自由度并联平台由动平台A1A2A3A4A5A6和静平台B1B2B3B4B5B6组成，采用半正六边形的形状，上下平台通过上、下连杆和球面副相连接，构成SPS结构，如图1所示。

本文在进行动力学分析时做了如下假设：

1)忽略各关节的摩擦力；

2)各刚体质量均匀；

3)各连杆关于各自的轴是对称的，且不能绕着各自的轴旋转；

4)动平台质心位于上铰点构成的平面的形心处。

在动、静平台的质心处分别建立坐标系OPxPyPzP、OBxByBzB。平台的矢量关系如图2所示，其中li为连杆的长度，ei为连杆的单位矢量，ai、bi为动、静平台上的铰点在各自平台坐标系的位置矢量，矢量P表示动平台质心在静平台坐标系的位置。动平台、上连杆和下连杆的质量分别为mP、ma和mb。

图1 并联平台SPS结构示意图

图2 连杆参数示意图

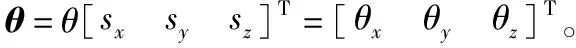
如图2所示，在下铰点Bi处建立依附于连杆的移动坐标系{Bi}，{Bi}的单位向量分别为ei、ti和ri，ti和ri定义为：

(4)

ri=ei×ti

(5)

则{Bi}相对于{OB}的旋转矩阵为[13]：

(6)

2.2 速度关系

根据图2所示的矢量关系可得：

liei=p+BRPai-bi

(7)

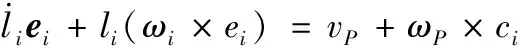
(8)

式(8)右边为上铰点的速度，其与动平台空间速度q的关系为：

(9)

(10)

用ei对式(8)两边同时进行叉积运算，并认为连杆不能绕着ei方向的轴旋转，整理后可以得到各连杆的角速度为：

(11)

将式(9)代入式(11)，整理后可得到：

(12)

根据图2所示几何关系可得上连杆质心速度为：

(13)

同理可得下连杆的速度为：

(14)

2.3 加速度关系

对式(11)两边求导可得支腿伸缩运动的加速度为：

(15)

对式(9)两边求导可得上铰点加速度为：

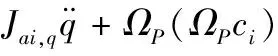
(16)

式(16)中，ΩP为ωP的反对称矩阵。

对式(13)两边求导可得上连杆质心加速度为：

(17)

其中：

(18)

(19)

同理可得：

(20)

(21)

3 基于Kane方程的动力学建模

3.1 偏速度和偏角速度

上连杆的偏速度矩阵为：

(22)

下连杆的偏速度矩阵为：

(23)

上、下连杆具有相同的偏角速度矩阵，均为：

(24)

动平台的偏速度矩阵和偏角速度矩阵分别为：

(25)

(26)

3.2 广义主动力

在不考虑负载和其他干扰力的情况下，并联平台的主动力包括：动平台和连杆的重力以及连杆上的驱动力。

(27)

进一步在偏速度矩阵的基础上，可以给出上连杆重力的广义主动力矩阵为：

(28)

同理可以得到下连杆重力的广义主动力矩阵为：

(29)

动平台重力的广义主动力矩阵为：

(30)

六个支腿上的驱动力向量τ作用在上连杆上，其对应的广义主动力为：

(31)

3.3 广义惯性力

上连杆质心运动产生的惯性力为：

(32)

参考广义主动力矩阵的形式，结合式(22)可以得到上连杆质心运动的广义惯性力矩阵为：

(33)

同理可以得到下连杆质心运动的广义惯性力矩阵为：

(34)

上、下连杆转动产生的惯性力为：

(35)

(36)

(37)

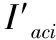
结合式(24)，其对应的广义惯性力矩阵为：

(38)

式(38)中，skew(Peivai)为Peivai的反对称矩阵。

动平台质心运动产生的惯性力为：

(39)

动平台转动产生的惯性力为：

(40)

(41)

3.4 并联平台封闭动力学模型

根据Kane方程，将求得的广义主动力和广义惯性力代入式(1)可得：

(42)

进一步整理得：

(43)

(44)

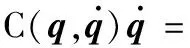
(Mai+Mbi+Mai,bi)ΩP(ΩPci)+CP

(45)

(46)

至此得到了六自由度并联平台完整的封闭动力学方程。

4 仿真验证

给定并联平台中各刚体的几何参数，如表1所示。分别在式(43)表示的动力学方程下，考察并联平台的前向动力学仿真和逆动力学仿真以验证模型的正确性。

表1 并联平台的几何参数

前向动力学仿真即已知驱动力，求解动平台的运动轨迹。利用计算力矩法[13]控制动平台跟踪式(47)和式(48)所示的轨迹，且不考虑模型的建模误差，动平台的初始高度为0.65 m，其余初始状态均为0，利用四阶龙格库塔法求解，实际轨迹和输出轨迹如图3和图4所示。

(47)

(48)

逆向动力学即在给定轨迹下，求解所需的驱动力。考察并联平台在式(47)和式(48)所示的轨迹下的驱动力变化。驱动力变化曲线如图5和图6所示。

从前向动力学仿真和逆动力学仿真的结果可以看出，并联平台的运动和驱动力变化是符合预期的，表明本文利用Kane方程建模的正确性。

图3 动平台位置的期望和输出轨迹

图4 动平台姿态的期望和输出轨迹

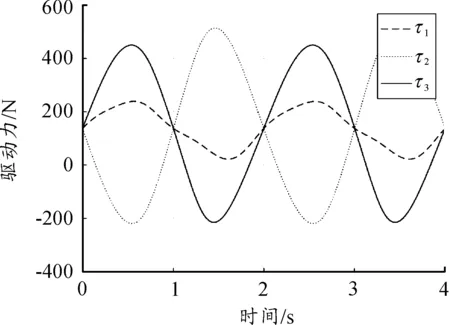
图5 连杆1-3驱动力变化曲线

图6 连杆4-6驱动力变化曲线

5 结论

1)用螺旋坐标描述动平台的空间姿态，使动平台空间位姿的导数和空间速度具有直接的对应关系，避免了额外的转换过程；

2)通过建立偏速度矩阵和偏角速度矩阵推导了Kane方程中各变量具体的表达式，并对动平台和连杆相对质心的惯量矩阵计算做出了说明；

3)根据Kane方程建立了六自由度并联平台的动力学模型，通过仿真验证了模型的正确性。