复杂地形单兵无人机精准投弹稳定控制研究

王胜男,陈 放

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

在我方小规模部队在无我方部队空中、地面火力支援的情况下，可利用可小型单兵携带投弹无人机对复杂地形中的隐蔽目标进行视距外的有效打击。由于单兵携带的弹药量有限，为了利用最少的弹药达到最大的打击效果，就对弹药的投弹精准度提出了更高的要求。

为了解决无人机投掷非制导弹药命中精度低的问题，余超等[1]提出了一种跃升-俯冲投弹攻击方法，通过炸弹的运动学模型和无人机机动性能约束条件求解炸弹投放点，并设计了跃升-俯冲攻击的全过程航迹；田应元等[2]对影响落点散布的投弹条件进行了仿真计算，确定了各投弹条件对空投弹道的影响，其中飞机的位置坐标以及角度的偏差对落点的散布影响较大；程善政等[3]分析了投弹初始条件对弹伞系统入水参数的影响，得到低空低速的投弹方式对入水点散布的影响较小；王昊鹏等[4]建立了基于测距法的轰炸光电瞄准模型，该模型能够稳定解算瞄准诸元。

在本文的应用场景下，由于在单兵携带的小型投弹无人机上搭载了多枚弹药，在悬停飞行且连续投弹的过程中，其重心的位置发生改变，整机质量产生突变，在这一过程中的扰动会影响投弹的初始条件，从而对投弹精准度产生影响。为减小投弹初始条件的误差，本文在飞行原理的基础上建立单兵投弹无人机不平衡负载下的动力学模型并搭建仿真平台，针对投弹过程中的不平衡负载突变的情况，分别建立PID控制、串级PID控制和串级模糊PID控制模型来降低弹丸投弹时的初始扰动，仿真结果表明：串级模糊PID控制方法可有效提高落点的精确程度。

1 单兵投弹无人机不平衡负载下飞行动力学模型

建立惯性坐标系E(OXYZ)和机体坐标系B(oxyz)，惯性坐标系E与地球表面固连，机体坐标系B与无人机固连，无人机的形心为坐标原点，符合右手法则，如图1所示。

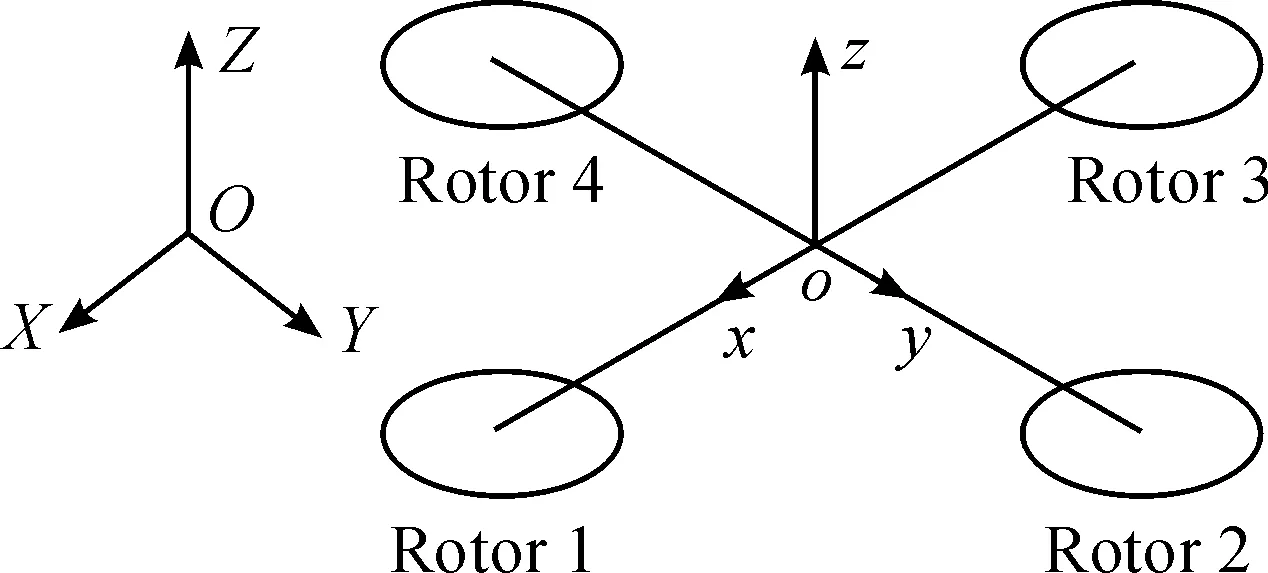
图1 小型投弹无人机机体坐标系以及地面坐标系

对无人机的飞行姿态进行更精准的描述，根据图2，定义欧拉角如下：

滚转角φ：机体坐标系绕ox轴所旋转的角度，顺时针为正，逆时针为负；

俯仰角θ：机体坐标系绕oy轴所旋转的角度，顺时针为正，逆时针为负；

偏航角ψ：机体坐标系绕oz轴所旋转的角度，顺时针为正，逆时针为负。

根据惯性坐标系E以及机体坐标系B和无人机3个姿态角的定义，从机体坐标系B(oxyz)到惯性坐标系E(OXYZ)的转换矩阵C为

C=CxCyCz=

(1)

为了方便建立单兵投弹无人机动力学模型，进行如下假设：无人机在飞行过程中可被认为是刚体，且机体均匀对称；无人机在整个飞行过程中，不受除了桨叶自身产生的气流之外的影响，默认当地气象条件无风雨；把坐标系的原点建立在无人机的几何中心上；机体所受到的空气阻力可以忽略不计；桨叶旋转所产生的升力与其转速的平方成正比，反扭矩与转速的平方成正比。

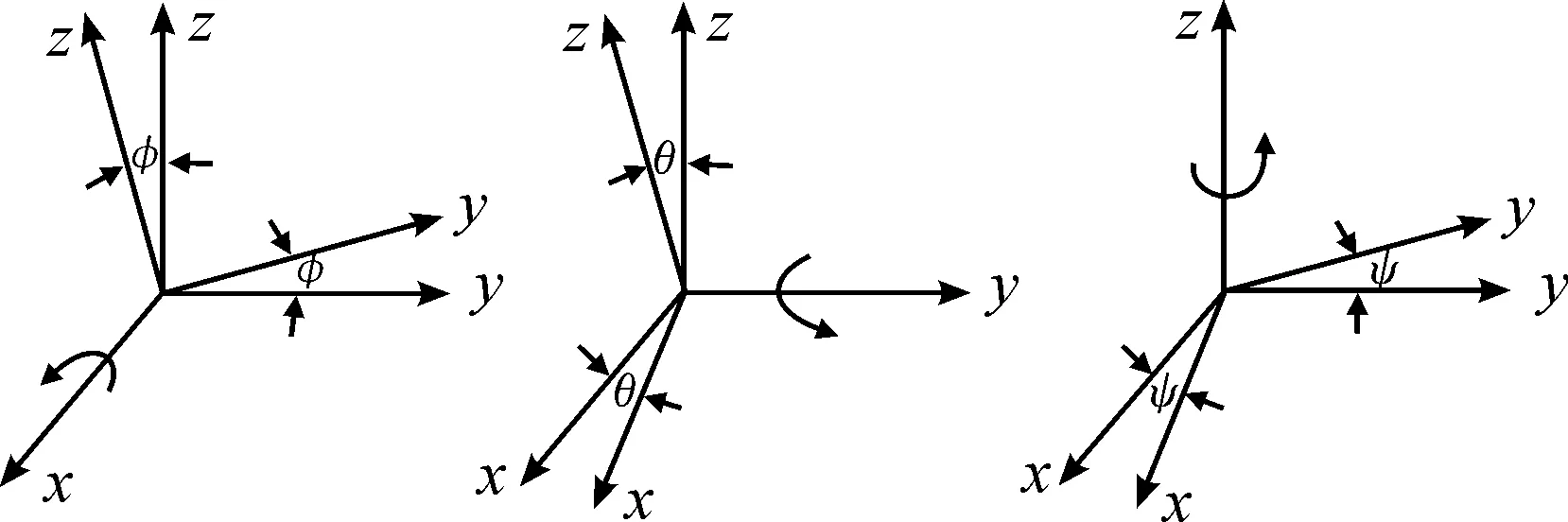
图2 欧拉角示意图

1.1 单兵投弹无人机质心运动模型

在无人机搭载弹药后，重心位置发生偏移，故重心由初始坐标o(0,0,0)迁移至o′(xa,ya,0)。根据受力分析可知，机体所受外力和力矩有无人机和所载弹丸的合重力G、四片桨叶所产生的升力Fi(i=1，2，3，4)，方向垂直桨叶向上，如图3所示。同时产生扭转力矩Mi(i=1，2，3，4)，方向垂直桨叶的旋转平面，与旋转矢量相反。

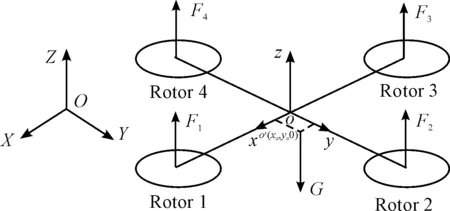
图3 单兵投弹无人机受力分析模型

桨叶的升力可表示为

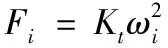
(2)

根据牛顿第二定律将无人机受力表现为式(3)：

(3)

根据上述受力分析、牛顿第二定律以及坐标系之间的转换矩阵，可得到投弹无人机的质心运动模型[5-6]：

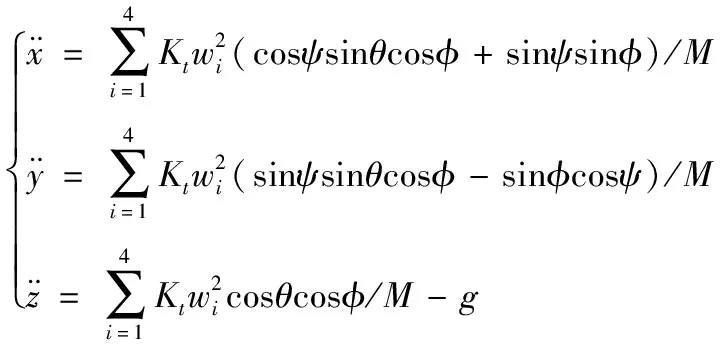
(4)

1.2 单兵投弹无人机姿态变化模型

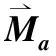
H为无人机相对于地面坐标系的绝对动量矩，由角动量定理可知，

(5)

在机体坐标系上对上式进行表示，则有相对导数，

(6)

设l为桨叶中心到坐标系远点的距离，故，

(7)

无人机的角动量矩为

(8)

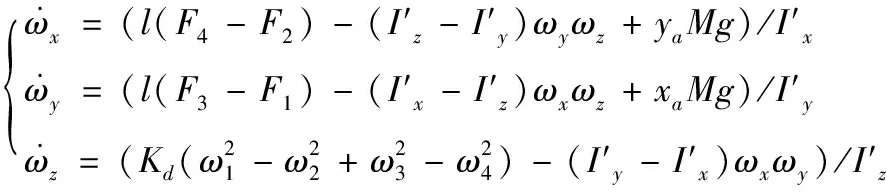
(9)

定义U1、U2、U3、U4分别为无人机的垂直、翻滚、俯仰、偏航控制量，来对其控制进行简化分析：

(10)

整理式(4)、式(9)、式(10)后可得单兵投弹无人机不平衡负载下的动力学模型：

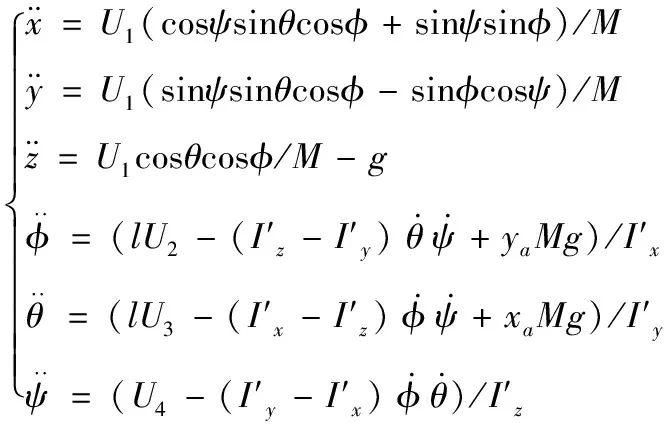
(11)

2 投弹初始条件稳定性控制建模

2.1 单兵投弹无人机参数

依据所搭载弹丸的基本信息以及前文建立的单兵投弹无人机模型，设计并匹配了一套单兵投弹无人机参数，详见表1。

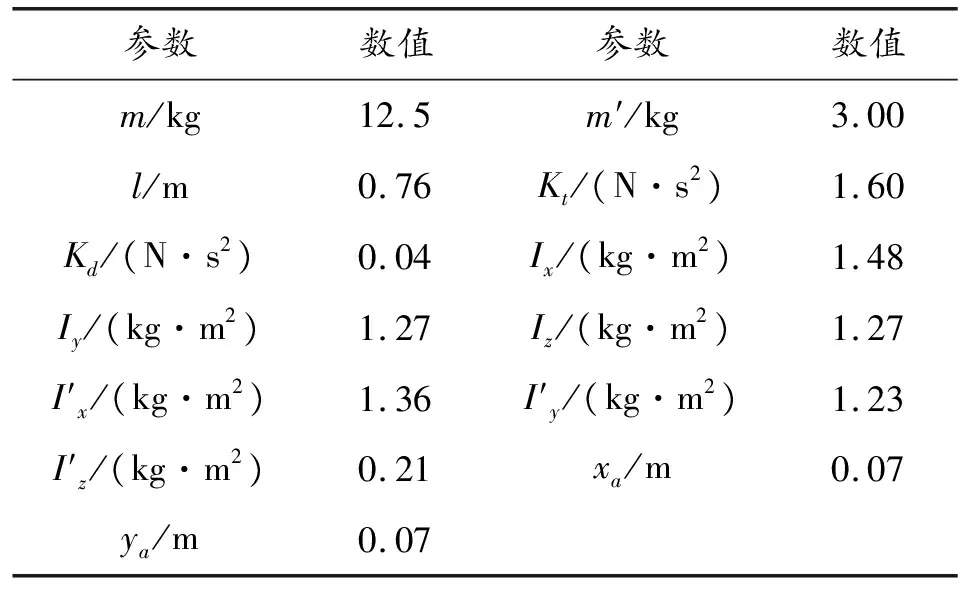
表1 单兵投弹无人机与搭载弹丸相关参数

对式(11)分析可知，姿态角的变化不依赖于无人机的位置变化，而无人机位置的变化依赖于欧拉角。因此，可将投弹初始条件的控制分为两个子模块：姿态控制模块和位置控制模块。

2.2 投弹初始条件稳定性PID控制建模

搭建PID控制的仿真回路如图4所示[7]，经过模型搭建与调试，获得经典PID控制下各通道的KP、KI、KD值，如表2所示。

图4 投弹初始条件稳定性PID控制框图

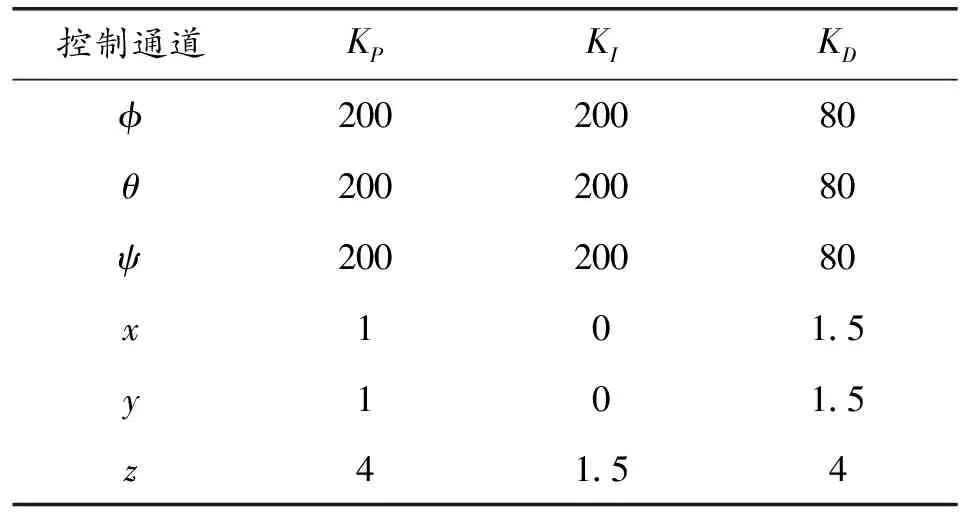
表2 PID仿真参数取值

2.3 投弹初始条件稳定性串级PID控制建模

对式(11)分析可知，当投弹无人机下方挂有不在其质心上的弹丸时，投放弹丸会使无人机的姿态角发生改变，为了进一步提高投弹初始条件的稳定性，考虑提出了角度/角速度协同的控制方案。搭建角度/角速度部分串级PID控制器如图5所示。

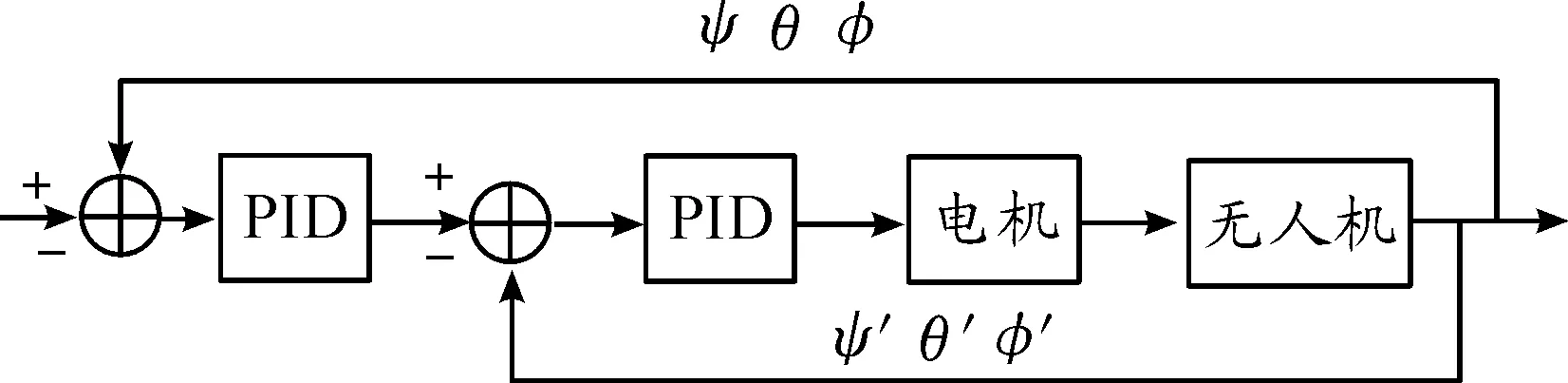
图5 投弹初始条件稳定性串级PID控制结构框图

在调试过程中发现，外环的PI控制器能够使系统快速无稳态误差的收敛，内环的PD控制器可有效抑制系统超调量，可以满足系统设计的要求。文献[8]表明：PI-PD控制器对于运行状态变化引起的模型误差和参数变化具有更强的鲁棒性。因此，调试获得串级PID控制下各通道的KP、KI、KD值，如表3所示。

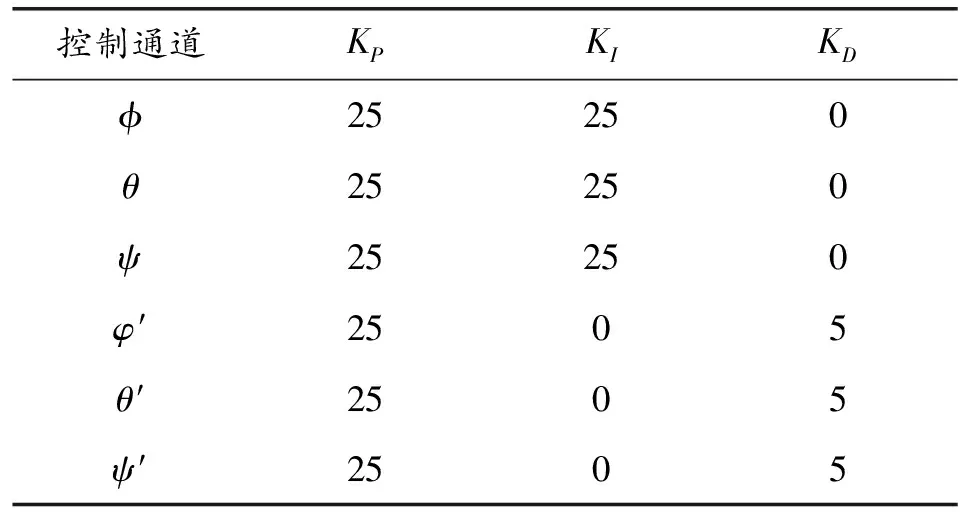
表3 串级PID仿真参数取值

2.4 投弹初始条件稳定性串级模糊PID控制系统构建

投弹无人机在投弹前后的数学模型会发生变化，因此，单一固定的PID参数不能使任意飞行状态(载弹/空载)时投弹的初始条件达到最佳状态。故考虑模糊PID控制方法，通过模糊规则来对系统实现动态调整，克服传统PID控制方法不能实时调参的缺陷[9-10]。

在串级PID基础上设计的串级模糊PID控制系统框图如图6，在Matlab/Simulink中，各个通道所建立的模糊子模块如图7所示。

图6 串级模糊PID控制系统框图

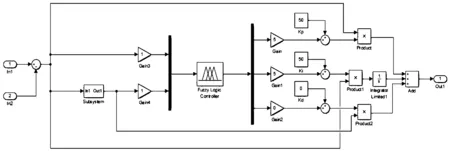
图7 模糊子模块示意图

在模糊子模块中，定义位置、角度、角速度控制环的偏差e、偏差变化率de、控制环输出量ΔKP、ΔKI、ΔKD的模糊子集为{NB,NM,NS,Z,PS,PM,PB},论域范围取{-3,3}，依据元素的取值情况和经验，NB选用Z型隶属函数，PB选取S型隶属函数，其余均选用三角形隶属函数，如图8所示。

模糊控制规则是模糊控制方法的核心，在本文中模糊控制规则主要是用来依据e和de确定输出量ΔKP、ΔKI、ΔKD来实现对系统的动态控制。根据KP、KI、KD对系统稳定性的影响以及三者之间的相互作用，设计PID控制模糊规则表，如表4所示。

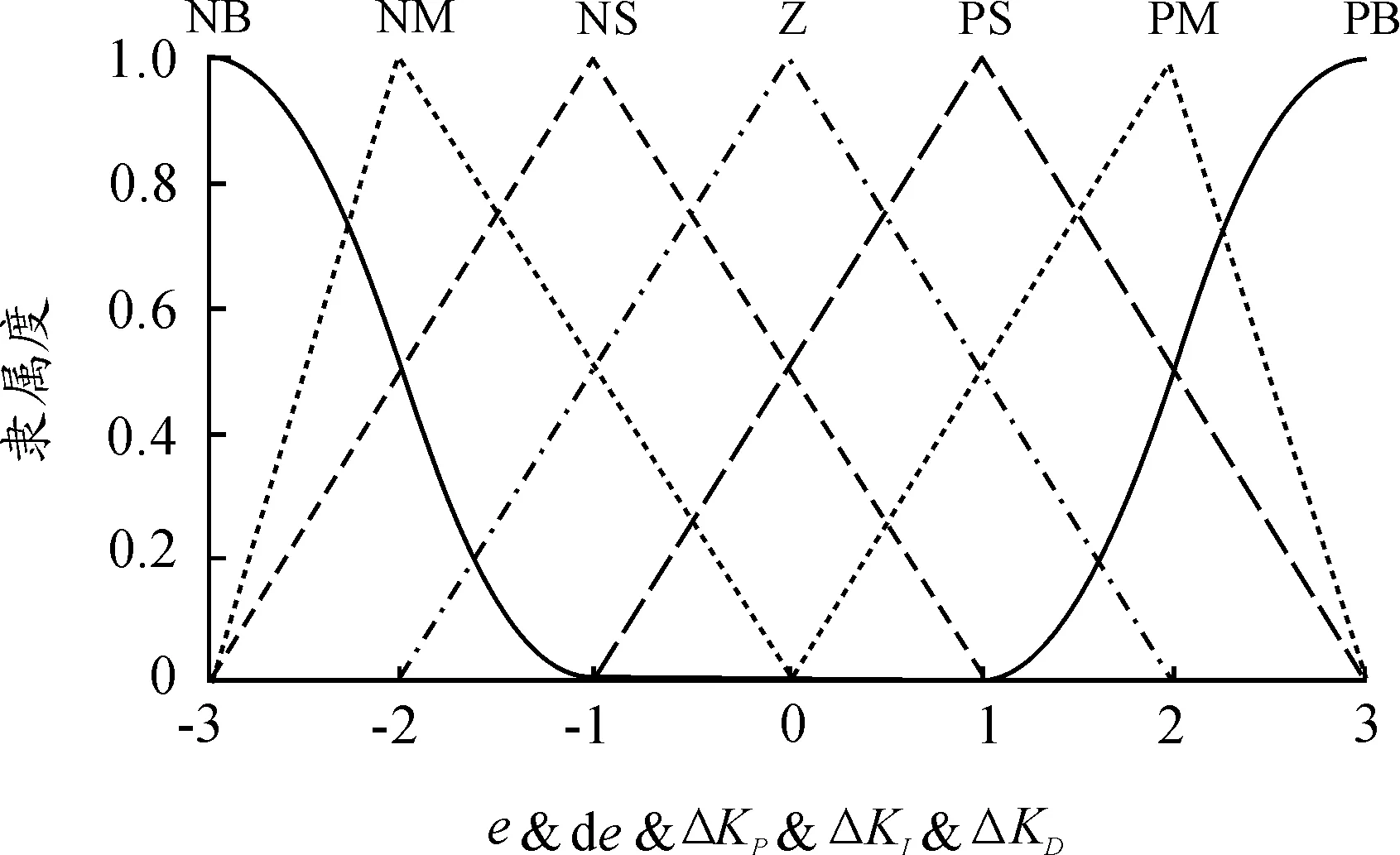
图8 隶属度函数曲线

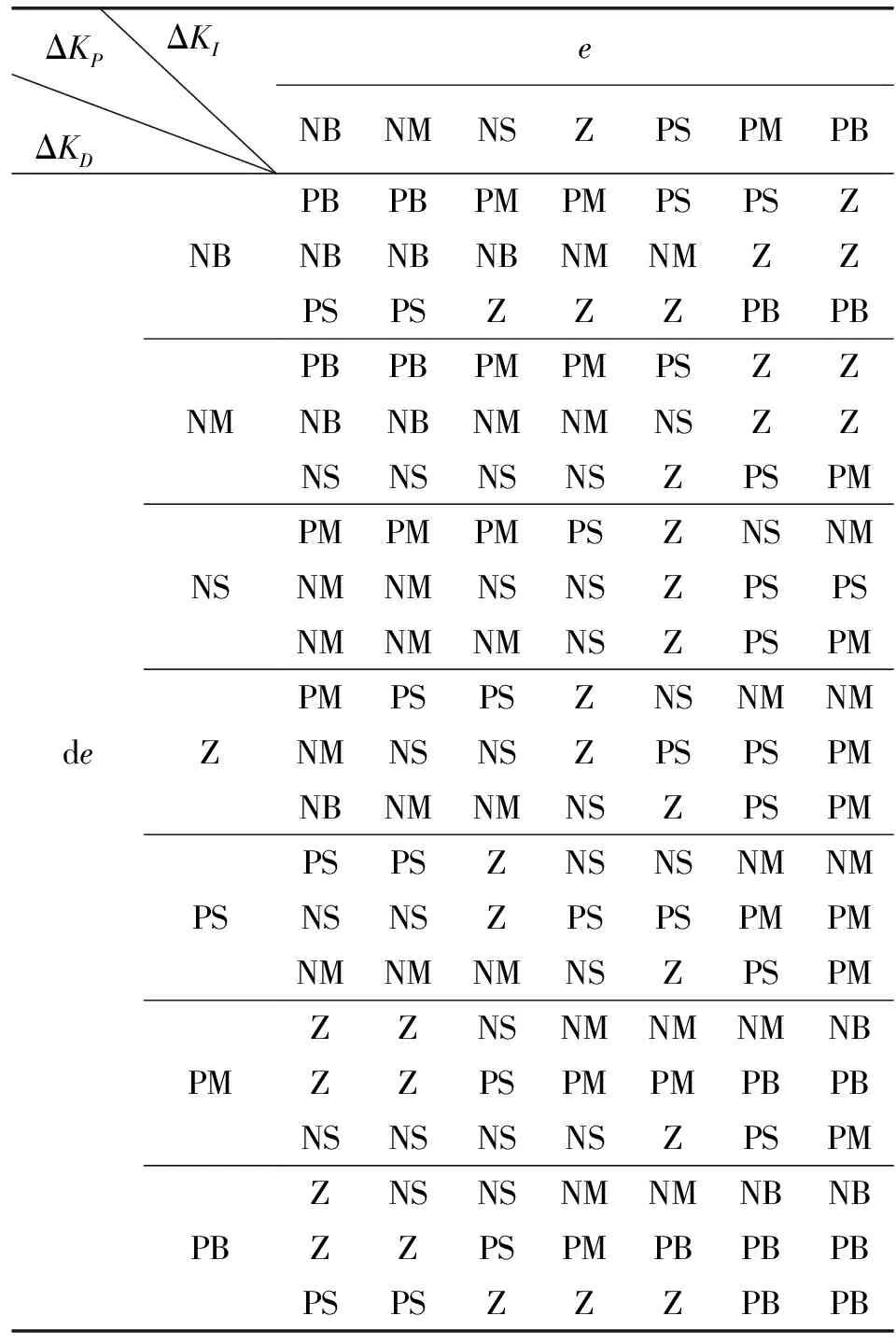
表4 PID参数模糊规则表

输入的偏差e和偏差变化率de与输出变量ΔKP、ΔKI、ΔKD之间的控制参数曲面如图9所示。

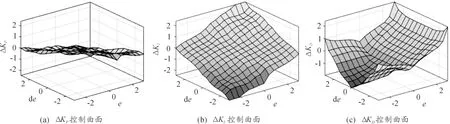
图9 输出变量控制曲面

当重心位置无法精确获得，模型参数则具有不确定性时，经过仿真测试，重心偏移量xa、ya在[-0.48l,0.48l]范围内时，模糊控制方法均可以对其进行稳定控制，可有效的抑制模型的参数不确定性。

3 投弹初始条件稳定性仿真分析

根据式(11)与图4、图5、图6，搭建Matlab/Simulink仿真模型，设置系统初始状态为x=y=z=0，φ=θ=ψ=0，在t=2 s时，利用switch和clock模块改变M、Ix、Iy、Iz、xa、ya，模拟投弹过程对无人机投弹初始稳定性的影响，具体改变量取值见表1。3种控制策略下四旋翼无人机在6个自由度上的动态响应对比如图10所示。

对图10分析可知，投弹无人机在初始条件下处于悬停稳定状态，t=2 s时，投弹动作使得投弹无人机和下一枚将要投放弹丸的位置和姿态角均不同于初始理想悬停状态，而这些改变将会对下一枚弹丸的投放产生影响。依据弹丸的投掷条件，简化弹丸质心运动微分方程：

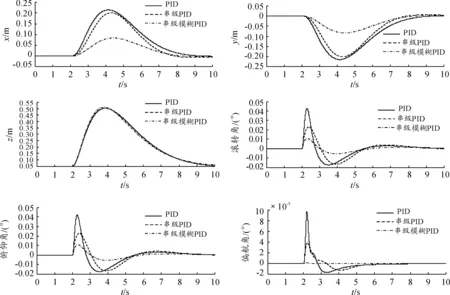
图10 投弹初始条件响应

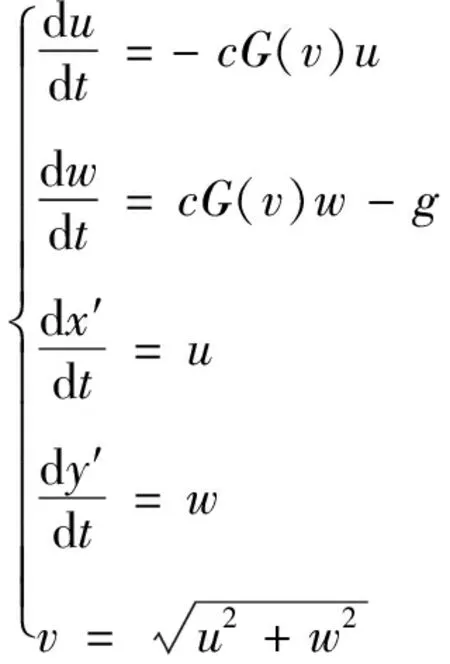
(12)

式(12)中：c为弹道系数；u,w分别为水平和垂直分量的速度；g为重力加速度；G(v)为阻力函数；(x′,y′)为弹丸的质心坐标，依据43年阻力定律，取G(v)=0.000 047v。

对式(12)分析可知，弹丸的初始状态vx、vy和vz对弹丸的落点影响最为明显。假设第1枚弹丸投放后1 s，投弹无人机释放第2枚弹丸，从仿真模型中获取3种控制方法下第2枚弹丸投掷时弹丸在惯性坐标系下的3个方向速度的vx、vy和vz，如表5所示。

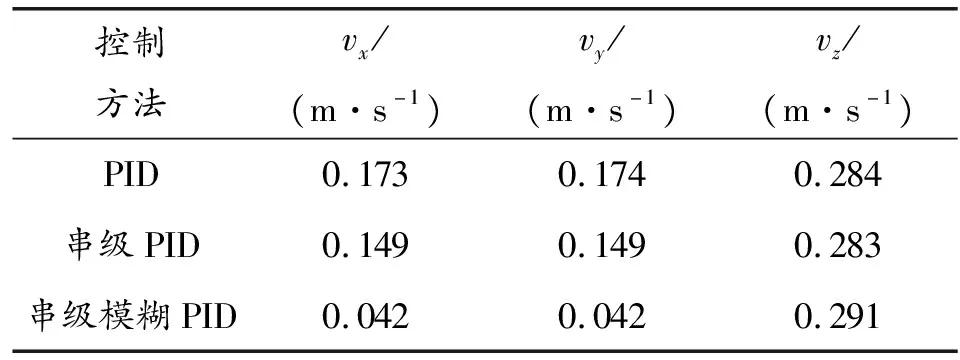
表5 第2枚弹丸的初始vx、vy和vz

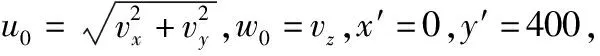
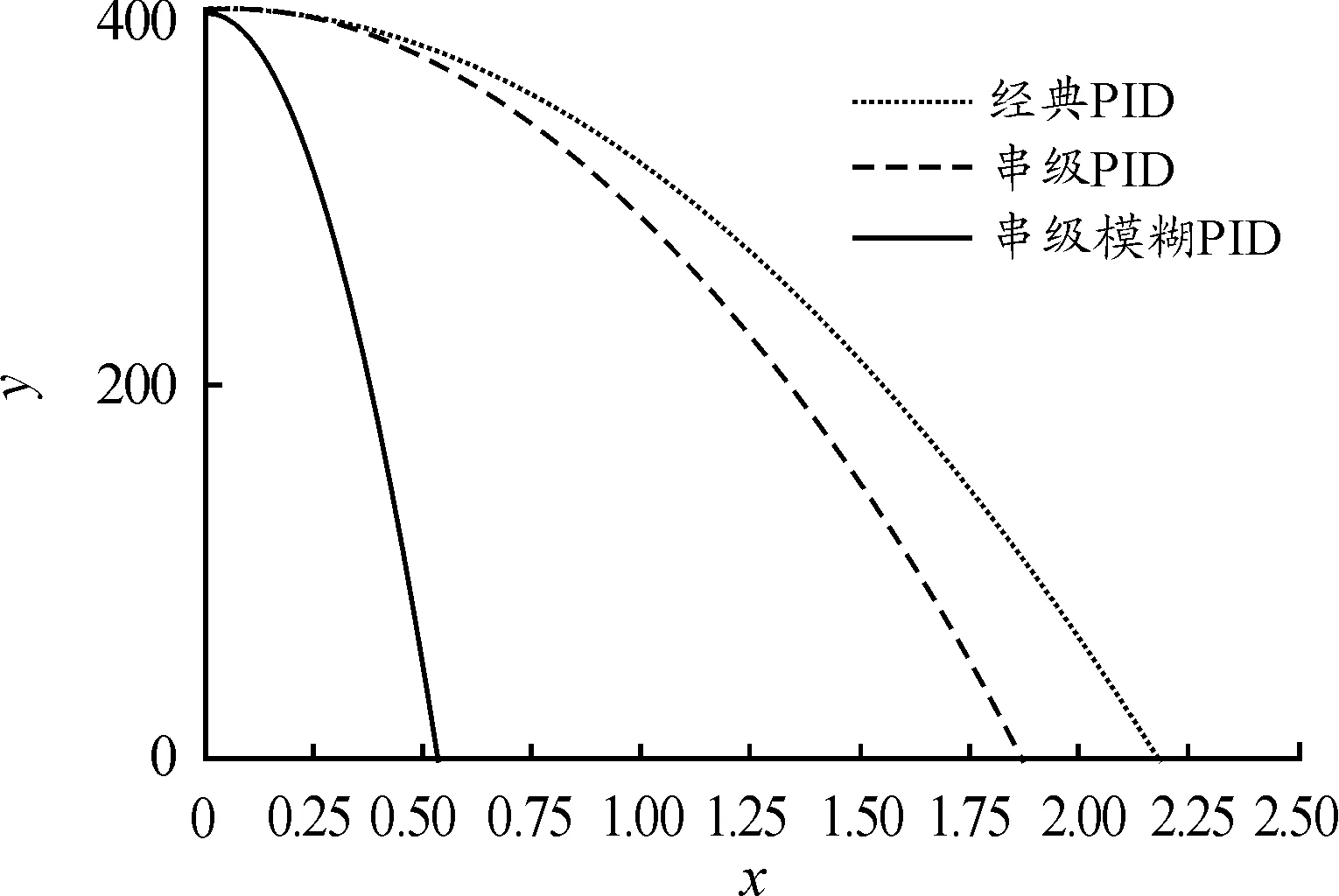
图11 弹丸运动轨迹对比图

经计算，弹丸约历时9 s落地，经典PID、串级PID和串级模糊PID 3种控制方法下，第2枚弹丸落点距离目标位置依次为2.18 m、1.87 m和0.52 m。串级模糊PID控制方法较经典PID控制方法对弹丸偏差减小了76%，较串级PID控制方法减小了72%。

4 结论

串级模糊PID控制方法对投弹初始条件的控制效果最优，相对经典PID控制方法，落点精度提高了76%，可有效提高单兵投弹无人机装备的投弹精准度。