基于贝叶斯概率模型的纤维混凝土梁受剪承载力预测
张广泰,张 梅,张路杨,曹银龙,陈 勇
(新疆大学建筑工程学院,乌鲁木齐 830046)
0 引 言
钢纤维混凝土梁受剪承载力预测是国内外学者研究的热点之一,但由于其影响因素众多、受力复杂,以及混凝土材料自身具有较大的离散性,至今尚未形成统一的受剪理论体系[1-2]。钢纤维混凝土梁受剪承载力计算方法主要为半经验半理论公式和基于力学模型的简化计算公式,但由于存在着主观不确定性,导致在预测承载能力时会产生偏差[3-5]。而贝叶斯理论通过引入影响钢纤维混凝土梁受剪因素的修正系数能较好的考虑主观、客观不确定性的影响,并能更加准确的预测构件的承载能力。
目前,在国内外已开展大量关于钢纤维混凝土梁受剪承载力的研究[6-10]。Ding等[6]对钢纤维混凝土梁进行了受剪承载力试验研究,探讨了钢纤维对梁的挠度、开裂、极限荷载和破坏形态的影响,以及钢纤维与箍筋的共同作用,并提出了一种基于修正压力场理论的钢纤维混凝土梁受剪承载力计算方法。焦楚杰等[7]研究了钢纤维体积率、剪跨比、配箍率及混凝土强度等级等因素对钢纤维轻骨料混凝土梁受剪承载力的影响,并在试验结果基础上, 通过数据回归分析, 建立了梁斜截面受剪承载力计算公式。徐旭炜等[8]研究了钢纤维掺量对混凝土梁受剪承载力的影响,并对我国CECS38:2004和欧洲RILEM TC162-TDF规程中钢纤维混凝土梁受剪承载力计算公式及计算结果进行了对比分析。熊毅[9]以钢纤维体积率为变量,对钢纤维再生混凝土梁的受剪承载力进行了试验研究,根据受剪承载力随钢纤维体积率的变化趋势拟合出相应关系的数学公式,并结合有关的国家规范总结出钢纤维再生混凝土承载力的理论规律和计算方法。Lim等[10]研究表明掺入钢纤维可减少构件所需的受剪箍筋数量,且钢纤维和箍筋的组合能较好满足梁延性和抗剪强度的要求,同时通过综合考虑混凝土强度、纤维体积率、剪跨比及配箍率等的影响,建立了预测钢纤维混凝土梁抗剪强度的分析方法。总体而言,上述研究建立的受剪承载力公式均考虑了混凝土强度、剪跨比及纤维体积率等因素的影响,但均为基于确定性模型建立的,忽略了纵筋、混凝土强度离散性、和尺寸效应等因素的随机性,导致计算结果离散性较大,计算精度和适用性有限。因此,有必要采用贝叶斯概率模型,综合考虑主观、客观不确定性的影响,建立钢纤维混凝土梁受剪承载力计算方法。
基于此,本文采用贝叶斯理论,结合先验模型和106组试验数据信息,建立了钢纤维混凝土梁受剪承载力概率模型,并将得到的计算值与试验值和我国《纤维混凝土结构技术规程》CECS 38:2004、欧洲RILEM TC 162-TDF规程中建议的计算公式计算结果进行了对比分析,验证了此模型的可行性和适用性,为钢纤维混凝土梁受剪承载力的准确预测提供了理论依据。
1 模型的建立
1.1 贝叶斯理论简介
贝叶斯假设:参数的先验分布应在其取值范围内服从均匀分布。在先验信息及贝叶斯假设的基础上,贝叶斯定理表达式为[11]:
(1)
式中:π(θ)为参数θ的先验分布;f(x|θ)为参数θ的后验分布。
贝叶斯推断是基于先验信息和样本信息的动态处理过程,其一般模式为:先验信息⊕样本信息推出后验信息,即π(θ)⊕p(x|θ)⟹π(θ|x),“⊕”表示贝叶斯定理的作用。
1.2 贝叶斯概率模型建立
以收集到的钢纤维混凝土梁的受剪承载力先验模型和数据信息作为先验信息,并考虑采用贝叶斯理论修正先验模型的误差,建立钢纤维混凝土梁受剪承载力概率模型:
V(x,Θ)=Vd(x)+γ(x,θ)+σε
(2)
式中:x为影响钢纤维混凝土梁受剪因素的向量形式,其需满足与公式方差σ2相互独立的条件;Θ=(θ,σ)为试验数据经过贝叶斯方法估计得到的模型参数;Vd(x)为现有钢纤维混凝土梁受剪承载力计算公式;γ(x,θ)为误差修正项;θ=[θ1,θ2, …,θp]T表示对x的修正系数;σ为修正模型存在的误差;ε是服从标准正态分布的随机变量。
用p个函数将误差修正方程γ(x,θ)线性表示为:
(3)
式中:hi(x)是根据理论和经验确定的一些基本函数。
将式(2)转化为对数形式表示为:
(4)
运用贝叶斯最大似然估计法与式(4)进行参数估计,可求得参数的后验估计。假设p(Θ)为参数Θ的先验分布,f(Θ)为后验分布,L(Θ)为试验数据的最大似然函数,则可得:
f(Θ)=κL(Θ)p(Θ)
(5)

由贝叶斯假设可知:对先验信息掌握不明确的情况下,参数的先验分布为[11]:
(6)
在满足上述内容的基础上,似然函数可表示为:
(7)
式中:φ(·)为正态分布概率密度函数;Φ(·)为正态分布函数;Vi为试验值;Vd(xi)为模型计算值。
破坏试验表示:Vi=Vd(xi)+γ(xi,θ)+σε;
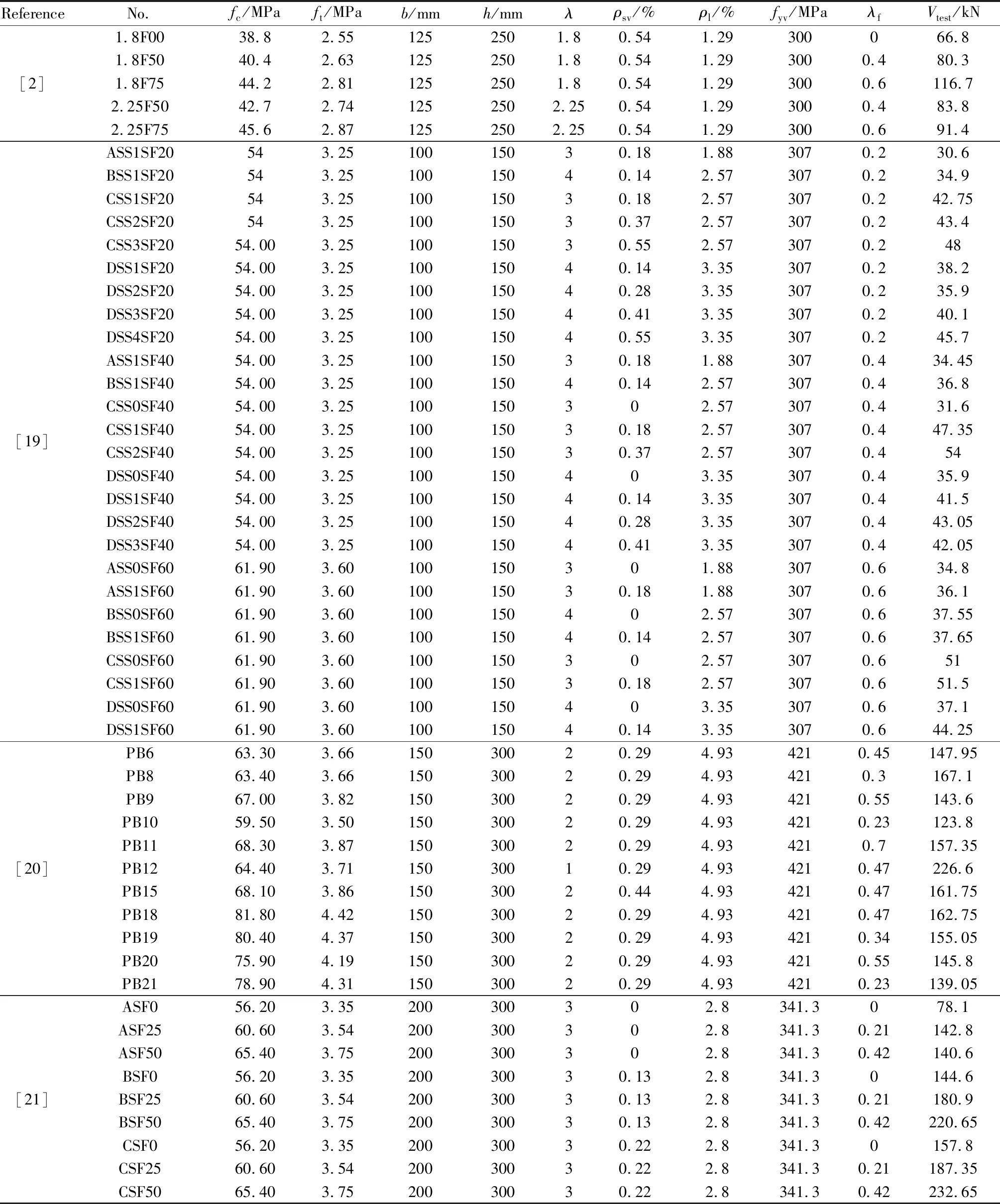
下界破坏表示:Vi 上界破坏表示:Vi>Vd(xi)+γ(xi,θ)+σε。 选取破坏试验为研究对象,基于上述先验分布的贝叶斯理论对其中未知参数进行估计,本文的概率模型形式可表示为: (8) 式中:hi(x)是由钢纤维混凝土梁受剪承载力影响因素确定。 通过查阅相关文献,对收集到的钢纤维混凝土梁受剪承载力影响因素进行统计分析,得到以下主要影响因素:混凝土强度、截面尺寸、剪跨比、箍筋配箍率、纵筋配筋率、箍筋屈服强度、纤维体积率及长径比;故hi(x)可确定为修正常数项h1(x)=ln2[12],h2(x)=lnfc,h3(x)=lnb,h4(x)=lnh,h5(x)=lnλ,h6(x)=lnρsv,h7(x)=lnρl,h8(x)=lnfyv,h9(x)=lnλf,h10(x)=lnft。 为综合考虑钢纤维混凝土梁受剪承载力的各影响因素,根据构件在混凝土强度、截面尺寸、剪跨比、箍筋配箍率、纵筋配筋率、箍筋屈服强度和纤维特征值等方面的差异,从近十年国内外相关文献[2,10,13-21]中收集了106组试验数据,其中混凝土抗压强度范围为37.8~122.4 MPa,混凝土抗拉强度范围为2.50~5.96 MPa,梁宽范围为100~400 mm,梁高范围为150~700 mm,剪跨比范围为1~4,箍筋配箍率范围为0%~1.41%,纵筋配筋率范围为1.29%~4.93%,箍筋屈服强度范围为0~641.9 MPa,纤维特征值范围为0~1.2,具体参数见表1。 以我国纤维混凝土结构技术规程(CECS 38:2004)和欧洲材料与结构联合会标准(RILEM TC 162-TDF)提出的钢纤维混凝土梁受剪承载力计算公式作为概率模型公式中的先验模型,采用贝叶斯理论分别对其因不确定因素产生的偏差进行修正,从而得到基于不同先验模型的钢纤维混凝土梁受剪承载力概率模型。 以我国CECS 38:2004建议的钢纤维混凝土梁受剪承载力计算公式为先验模型: (9) 式中:h0为截面有效高度;βv为钢纤维对钢筋钢纤维混凝土构件斜截面上与混凝土有关的受剪承载力的影响系数;Asv为箍筋截面积;s为箍筋间距。 基于CECS 38:2004建议的先验模型,结合表1中的试验数据,进行贝叶斯参数估计后得到的未简化概率模型如下式: (10) 表1 试验数据Table 1 Experimental data 续表1 注:fc为混凝土抗压强度;ft为混凝土抗拉强度;b、h为截面尺寸;λ为剪跨比;ρsv为箍筋配箍率;ρl为纵筋配筋率;fyv为箍筋屈服强度;λf纤维特征值,λf=Vflf/df,Vf为纤维体积率,lf/df为纤维长径比;Vtest为剪力实测值。 以欧洲RILEM TC 162-TDF建议的钢纤维混凝土梁受剪承载力计算公式为先验模型: VRd,3=Vcd+Vfd+Vwd (11) Vcd=[0.12K(100ρlffck)1/3+0.15σcp]bh0 (12) Vfd=KfKτfdbh0 (13) (14) 基于RILEM TC 162-TDF建议的先验模型,结合表1中的试验数据,进行贝叶斯参数估计后得到的未简化概率模型如下式: (15) 本文的10个受剪承载力影响因素中,部分因素对其影响不明显,故可采用贝叶斯参数剔除法剔除影响较小hi(x)以达到简化公式的目的,具体步骤如下: (1)计算参数θ=[θ1,θ2, …,θp]和σ的后验估计值。 (2)根据参数θ的后验分布计算每个hi(x)的变异系数C: C=σi/ui (16) 式中:σi为hi(x)的标准差;ui为hi(x)的均值。 (3)依次剔除θi对应的变异系数最大的hi(x),直至模型参数σ的后验估计值显著增大则停止参数剔除。具体参数剔除过程见表2和表3。 表2 基于中国规程的参数剔除过程Table 2 Parameter culling process based on Chinese specifications 表3 基于欧洲规程的参数剔除过程Table 3 Parameter culling process based on European specifications 由表2和表3可知,采用不同规程中建议的受剪承载力计算公式为先验模型进行参数剔除过程中,均依次剔除了对钢纤维混凝土梁承载力影响较小的h9(x)、h6(x)、h8(x)、h5(x)、h10(x)和h4(x),当剔除h7(x)时,σ2值显著增大,故h7(x)、h3(x)、h2(x)及h1(x)对其受剪承载力影响较大,不能剔除。基于两种先验模型的受剪承载力概率模型的简化公式为: (17) (18) 两种先验模型及其简化后的概率模型计算结果见表4,由表可知,试验值与两种先验模型计算值比值的均值为1.361、0.83,方差为0.152、0.06。试验值与两种修正后的概率模型计算值比值的均值为1.034、1.024,方差为0.077、0.05,由此可见,修正后概率模型的均值接近于1,且方差较小,能更为精确的预测钢纤维混凝土梁的受剪承载能力。图1、图2为试验值与修正前的先验模型计算值及修正后的后验概率模型计算值的对比分析图。由图可知,简化后的概率模型计算值与试验值的比值较两种先验模型更接近于1,计算值与试验值的偏差较小,采用不同先验模型进行贝叶斯估计后的计算值与试验值比值的整体分布情况相似。说明可采用贝叶斯方法对钢纤维混凝土梁受剪承载力进行无偏估计,且具有一定的优越性。 表4 试验计算结果Table 4 Experimental calculated results 续表4 图1 中国规程修正前后与试验值对比 图2 欧洲规程修正前后与试验值对比 (1)由采用贝叶斯概率模型建立钢纤维混凝土梁受剪承载力计算公式过程可见,中国CECS 38:2004规程和欧洲RILEM TC 162-TDF规程中建议的计算公式已较好考虑了配箍率、剪跨比、纤维因素以及箍筋屈服强度等的影响。 (2)基于贝叶斯概率模型建立的钢纤维混凝土梁受剪承载力计算公式的计算值较规程建议公式计算的承载力值更为接近试验值,且离散性较小,说明采用贝叶斯概率模型建立钢纤维混凝土梁受剪承载力计算公式具有合理性。 (3)文中建议的受剪承载力计算公式较好利用了先验模型和试验数据,避免了试验数据的离散性对其产生影响,同时可根据试验数据的不断积累对建议的受剪承载力计算方法进行实时更新。因此,本文建议的计算方法具有较好的准确性和完备性,且应用范围更为广泛。2 计算分析
2.1 影响因素选定及试验数据整理
2.2 后验模型建立

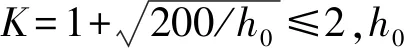
2.3 模型简化


2.4 计算结果及验证分析
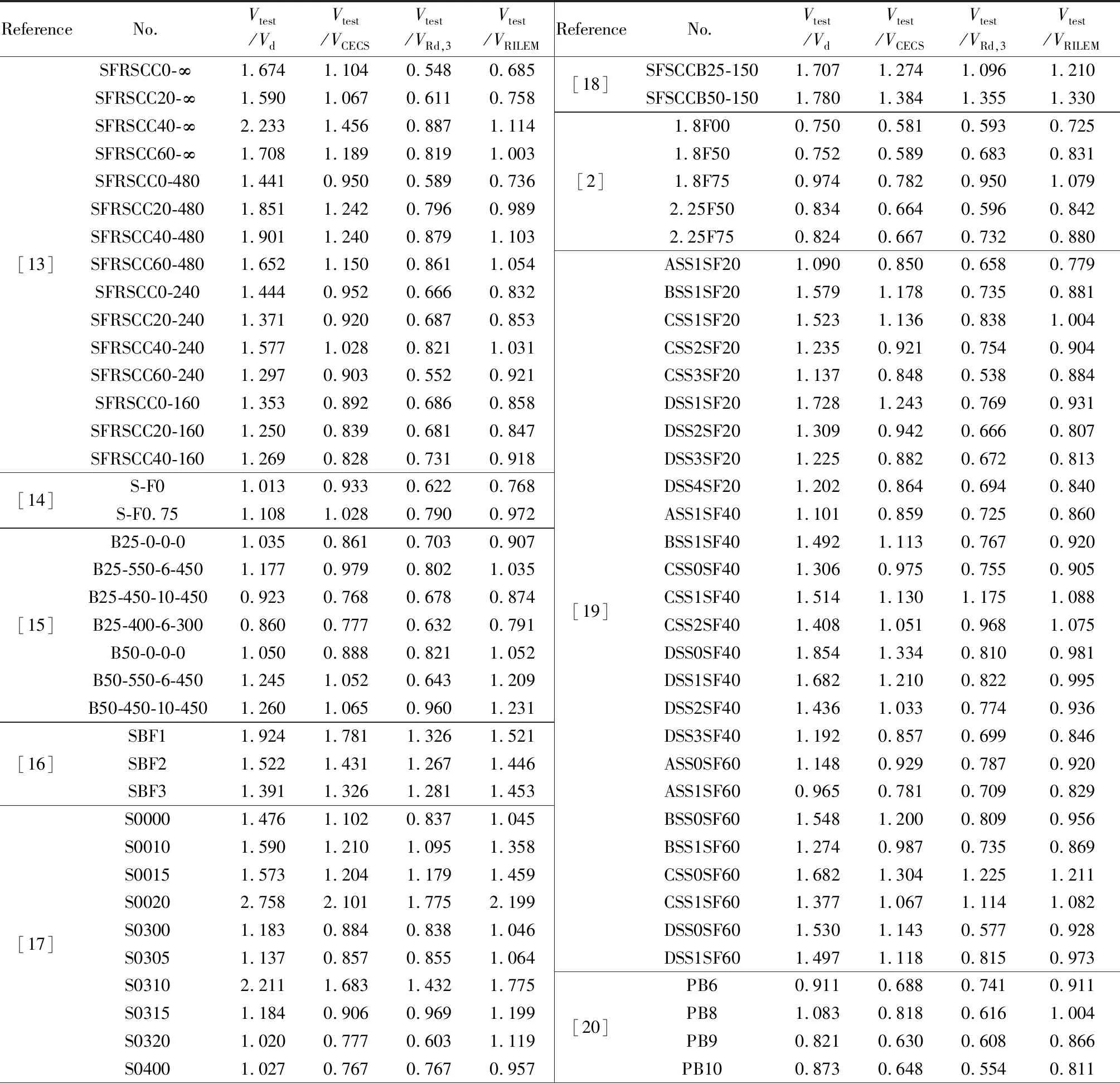
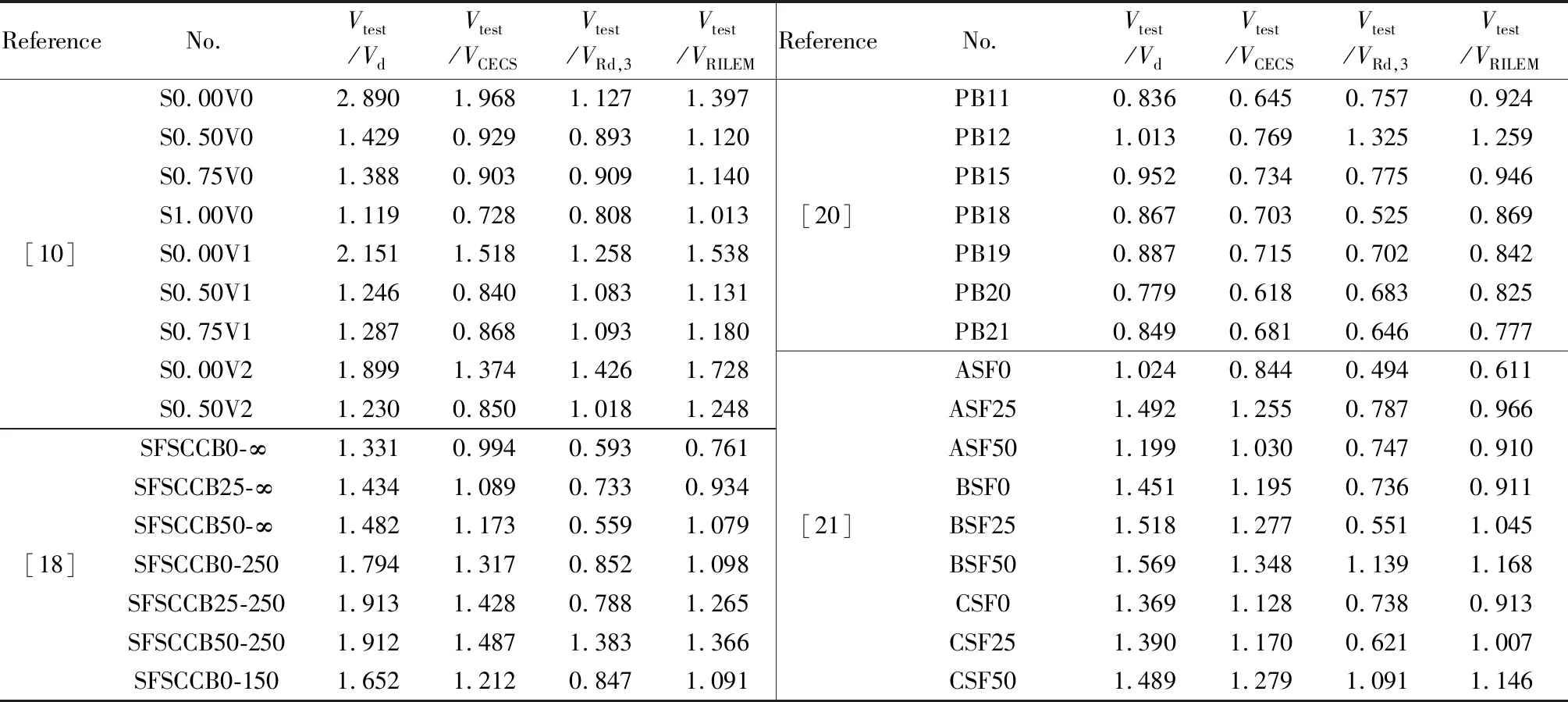
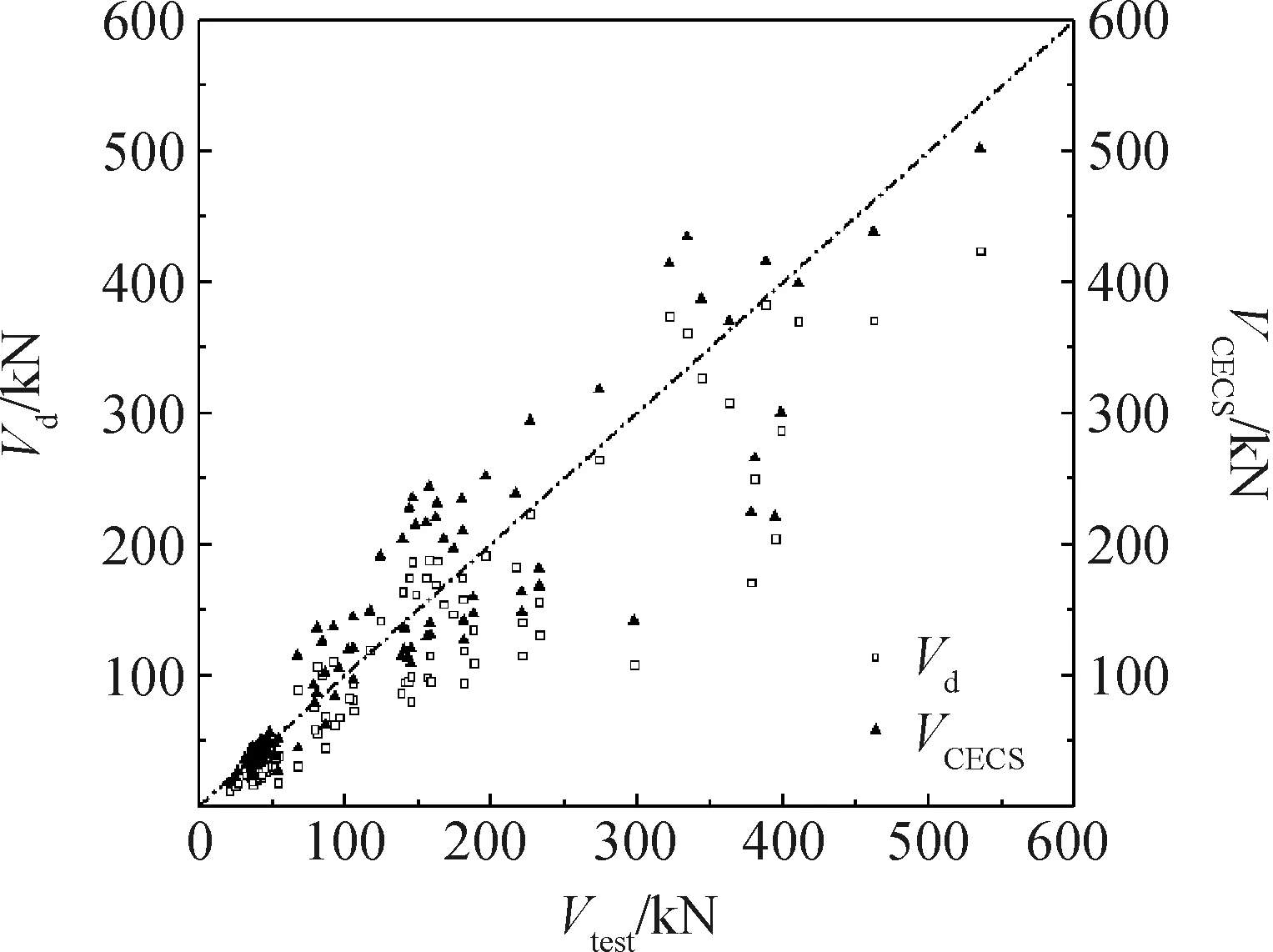
Fig.1 Comparison between Chinese procedures before and after revision with test values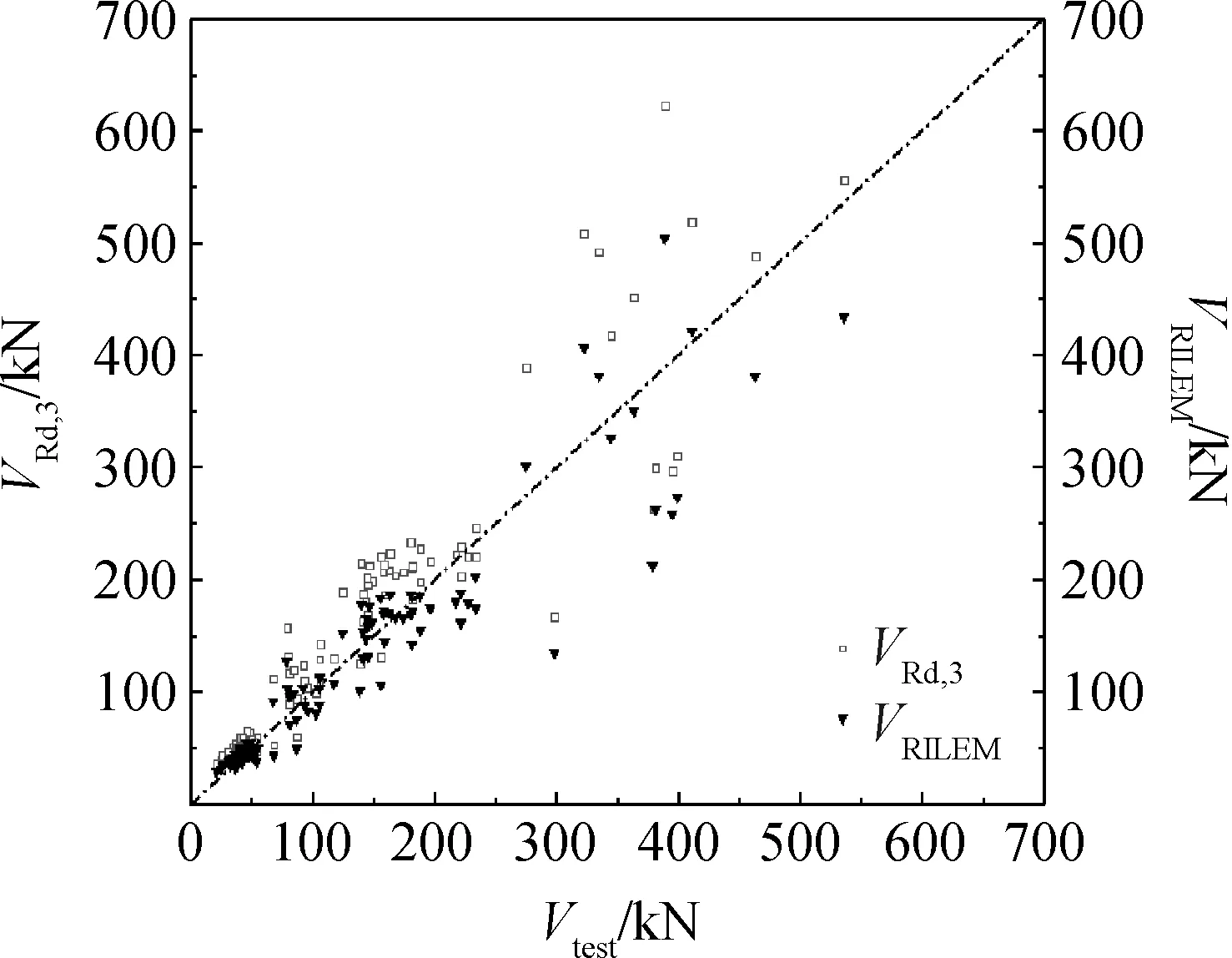
Fig.2 Comparison of European procedures before and after revision with test values3 结 论

