一种基于高斯核的多雷达联合检测方法
黄洁雅,李春霞
(1.中国传媒大学广播电视数字化教育部工程研究中心,北京 100024; 2.中国电子科技集团公司信息科学研究院,北京 100081)
1 引言
与单部雷达独立检测相比,多雷达联合检测具有更强的可靠性、生存能力和抗干扰能力,能有效扩展探测范围,满足未来探测体系的发展趋势[1][2]。常用均匀加权的平方律检测器[3]-[6]来融合多通道回波,当各通道回波具有相同的SNR时,平方律检测器具有最优的检测效果。然而,多通道回波可能具有不同的SNR,这也导致了平方律检测器的检测性能的降低。
针对这种情况,论文[7]提出一种基于信噪比加权的信号融合检测算法,在已知各通道回波SNR的情况下,该算法可达到检测性能的上界。但是,各通道回波SNR的估计的误差会导致该算法检测性能的下降。对此,论文[8]提出平方律检测和功率熵检测相结合的多雷达混合检测算法,当各通道回波SNR存在差异时,该算法始终具有最佳的检测性能。但由于该算法采用了“或”准则进行融合,在提升系统检测概率的同时也会导致虚警概率较高。
高斯核是支持向量机(SVM)[9]-[11]中常用的核函数,广泛用于雷达目标检测[12]-[14]。 但是,高斯核并未单独应用于多雷达检测。
在本文中,我们提出并分析了一种基于高斯核的多雷达联合检测算法。预期在各通道回波SNR未知的情况下,该算法也能通过调节核半径参数实现最优的检测性能。
2 方法
2.1 问题描述
考虑一个多雷达系统中存在n个空间分布的雷达R1,R2,…,Rn构成,每个雷达除接收自己发射信号的回波外,还接收其他雷达发射信号的回波,形成N(N=n×n)个通道的回波。
假设第i个通道在k时刻的回波信号为xi(k),则雷达信号融合中心的目标检测问题可通过以下二元假设检验表示:
(1)
其中,si(k)表示在H1条件下第i个通道在k时刻接收到的目标回波信号,对应的噪声信号ni(k)服从均值为0方差为σ2的复高斯分布,并且假定每个通道的噪声的方差相同。
2.2 算法描述
高斯核函数可以将样本映射到高维空间以测量相似度[10]。以下是高斯核函数的定义
(2)
其中,x,x′∈Rn是样本点,核半径ω>0。
在我们讨论的多雷达系统中,每个通道的回波经过平方律检波后,得到与之对应的回波功率。因此,信号融合中心接收到一组回波功率|x1(k)|2,|x2(k)|2,…,|xN(k)|2之后,信号融合中心可以根据这组回波功率,得到这组回波功率的最大值Max(k)=max{|x1(k)|2,|x2(k)|2,…,|xN(k)|2}和最小值Min(k)=min{|x1(k)|2,|x2(k)|2,…,|xN(k)|2}。
当利用这组回波功率的最大值时,信号融合中心设定的固定值m(k)=Max(k)。根据式(2),回波功率|xi(k)|2与固定值m(k)在高维空间中的相似度为
(3)
此时,在特定的核半径ω下,|xi(k)|2越大,越接近m(k),回波功率|xi(k)|2与固定值m(k)在高维空间中的相似度越大。因此,在k时刻第i个信道基于高斯核的权值表示为
(4)
当利用回波功率的最小值时,信号融合中心设定的固定值m(k)=Min(k)。那么,回波功率|xi(k)|2与固定值m(k)在高维空间中的相似度为
(5)
同样,在特定的核半径ω下,|xi(k)|2越小,越接近m(k),回波功率|xi(k)|2与固定值m(k)在高维空间中的相似度越大。因此,在k时刻第i个信道基于高斯核的权值表示为
(6)
根据信号融合中心设置的固定值以及对应的权值可以得到,在k时刻基于高斯核的检测统计量T(k)表示为
(7)
根据虚警概率Pfa的设定,可以得到检测门限Th,将检测统计量 与检测门限T(k)进行比较。假如,检测统计量T(k)大于检测门限Th,判定存在目标(H1);否则,判断不存在目标(H0)。
H1:T(k)≥Th
H0:T(k) (8) 已知Min(k)≤|xi(k)|2≤Max(k),当信号融合中心设定的固定值m(k)=Max(k)时,结合式(3)(4)(7)可以得到 (9) (10) 当信号融合中心设定的固定值m(k)=Min(k)时,结合式(5)(6)(7)可以得到 (11) (12) (13) (14) 可以得到,ω→0时,G的取值最大。 以上可以说明,在各通道的SNR均相同或近似相同的情况下,当固定值采用最大回波功率时,核半径越大,检测性能越好,并且当核半径取到足够大时,所提算法的检测性能接近平方律检测;反之,当固定值采用最小回波功率时,核半径越小,检测性能越好,并且当核半径取到足够小时,所提算法的检测性能接近平方律检测。对于在各通道的SNR差异较大的情况下,当固定值采用最大回波功率时,核半径越小,检测性能越好,并且核半径在一定范围内时,所提算法的检测性能优于平方律检测;反之,当固定值采用最小回波功率时,核半径越大,检测性能越好,同样核半径在一定范围内时,所提算法的检测性能优于平方律检测 在本节中,我们验证了所提算法中核半径的选择问题,并与平方律检测器进行对比。假设多雷达系统中雷达数为5,仅考虑空间多样性,形成的回波通道数为25,同时假设各通道的目标回波相位θ服从均匀分布,雷达目标不起伏。 在如下表所示的5种SNR比例下得到所提算法在取不同核半径参数时的仿真结果,并与平方律检测进行对比。 表1 多通道SNR比例 由于所提算法没有检测概率Pd和虚警概率Pfa的一般表达式,因此我们设定虚警概率Pfa=10-4,通过蒙特卡罗方法来验证所提算法在目标检测中的性能。仿真得到如图1-图5所示的仿真结果图。 图1 序号1的仿真结果图 图2 序号2的仿真结果图 图5 序号5的仿真结果图 从图1-图5获得以下结果: (1)从图1、图3可以看出,在每个通道的SNR均相同或近似相同的情况下,当所提算法中的固定值设为多通道回波功率的最大值时,核半径越大,检测性能越接近平方律检测,并且核半径取足够大的值时,所提算法的检测结果与平方律检测的检测结果一致,达到最优的检测效果;当所提算法采用各通道中回波功率的最小值时,核半径越小,检测性能越接近平方律检测,并且核半径取足够小的值时,所提算法的检测结果与平方律检测的检测结果一致,达到最优的检测效果。 (2)从图2、图4和图5可以看出,在各通道SNR存在较大差异的情况下,当所提算法中的固定值设为多通道回波功率的最大值时,核半径越小,检测性能越好,且核半径小到一定程度后会优于平方律检测;当所提算法中的固定值设为多通道回波功率的最小值时,核半径越大,检测性能越好,且核半径大到一定程度后会优于平方律检测。使用多通道回波功率的最大值作为固定值进行所提算法和使用多通道回波功率的最小值作为固定值进行所提算法,两者相比,使用最大值实现的最优检测性能总是略优于使用最小值实现的检测性能。 综上所述,在各通道信噪比未知的情况下,无论各通道信噪比是否相同,所提出的算法均可以通过调节核半径参数,使自身具有最佳的检测性能。 在多雷达系统中,由多个雷达形成的多通道回波可能具有不同的SNR。在这种情况下,基于Neman Pearson准则,提出了一种基于高斯核的多雷达检测方法。当信道的信噪比未知时,该方法可以调整核半径参数,使检测性能达到该方法的检测性能的上限。2.3 核半径的选择

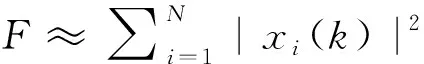
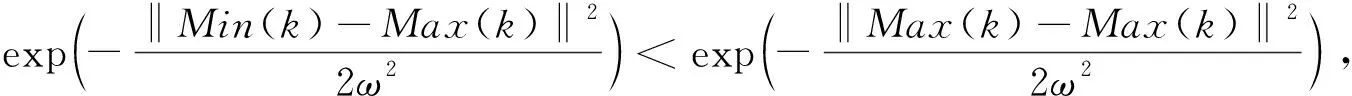



3 数值仿真



4 结论

