从声激波到光激波

黄志洵

(中国传媒大学信息工程学院，北京100024)

1 引言

在英文字典中，shock一词是指震动和冲击，而shock waves是指“region of intensely high air pressure caused by an atomic explosion or an aircraft moving at supersonic speed”(由原子爆炸或飞机以超声速飞行造成的剧烈的高空气压强区域)，通常译作激波。在严格的意义上，激波定义为媒质的物理参数(压强、密度、温度)在波阵面上发生突跃变化的压缩波，可发生于气体、液体和固体内。

激波是微扰动(如弱压缩波)的叠加而形成的强间断，有很强的非线性效应。由于激波，气体的压强、密度、温度都突然升高，流速则突然下降。实际的激波层有厚度，但很小。激波层对飞机造成很大阻力。……不过，对航天器重返大气层而言，由于帮助减速，激波又被看成有益的。……以上的描述针对的是常见的声激波(sonic shock waves，SSW)。

其实激波是自然界一种普遍存在的现象，其广泛性使人吃惊。实际上，已经知道在多个科学领域中，色散激波(dispersive shock waves，DSW)的形成已是一种基础性机制，例如在水力学、地球物理学、大气科学、化学、声学、量子流体及非线性光学中。自然界最吸引人的DSW显现是最常见的MT波，它产生于特定的河口，是由于潮汐与流动之间的作用。在大气层的气流中，对于某些特定的云和山间波动，DSW也会显现。通常DSW发生在保守(或弱色散)系统，具备两个要素：非线性和波的色散性。

光激波(light shock waves，LSW)的存在是不容置疑的。虽然过去所报告的现象多数在光纤中，但我们相信当飞船在宇宙的真空环境中飞行时，所谓“新以太”将像空气对飞机的作用那样，当接近光速时会出现与SSW类似的LSW现象。对这些问题我们将作初步的讨论。

2 声激波的形成和克服

20世纪是航空、航天技术从无到有从弱到强的世纪。世纪初发明的飞机很快就进步为生产民用、军用飞行器的庞大的航空工业，既丰富了人类生活又改变了战争模式。飞机速度的提高促进了空气动力学的发展[1]，没有坚实的理论基础就什么也做不了。航空界经历了从亚声速到超声速乃至高超声速的发展过程，与此同时人类又在20世纪后半期实现了航天技术的惊人进展；在1969年人上月球之后，如今已在筹划派人去火星。……相关的理论建树和技术进步都纪录在无数文献之中。

航空器发展的3个阶段是按速度区分的。规定Mach数为速度v与声速c的比值(Ma=v/c)，则3个阶段的划分为：亚声速(vc，Ma>1)；高超声速(v>5c，Ma>5)。在不同阶段，理论表述和技术面貌都不同，各有特色。当然，标志性的事件是1947年10月超声速飞机试飞成功，它是一个具有非凡意义的里程碑。

在飞机只能作低亚声速(vㄍc，Maㄍ1)飞行的时期，根本没有人想到能以v≥c的速度飞行。由于声波是微弱扰动波的一种，通常把微弱扰动的传播速度称为声速。对于不可压缩流体而言，体积不能改变，与刚体无异，故扰动传播速度为无限大。但空气是可压缩流，是弹性媒质，扰动速度不是无限大，声速的计算公式为

(1)

式中的常数(γ、R)由气体种类决定，T是热力学温度。海平面高度下标准大气(T=288K)c=341m/s，离地面10km高度处的空气(T=223K)c=300m/s。

那么声障(sonic barrier)一词从何而来？它是否与理论无关的纯经验性概念？它与光障(light barrier)概念是否有“根本上的不同”？为了讨论的方便，相对速度v/c也使用符号β；亦即在声学问题中β=Ma=v/c(c是声速)，在光学问题中β=v/c(c是光速)。

空气动力学的发展过程中有几个方面与讨论相对论、超光速时的情况相类似。在低亚声速的早期，流速低，压力、密度变化小，流体近似看成不可压，速度势、流函数满足Laplace方程。速度提高后，用小扰动理论，气体质量密度ρ随速度v加大而增加，通常认为

(2)

式中ρ0是静止时的质量密度；上式与狭义相对论(SR)中的质速公式完全一样。当v=c、β=1，出现奇点(密度成为无限大)。这就是声障概念的来源；但它并非不可突破。

现在看一下力学、声学、电磁学这3个领域的情况，了解如何通过数理方程(微分方程)认识它们的共性。表1给出了数理方程的几种类型。从理论上讲，空气动力学存在强非线性表达方式，但如把强非线性数学问题简化为小扰动线性方程来求解，就会出现奇点。

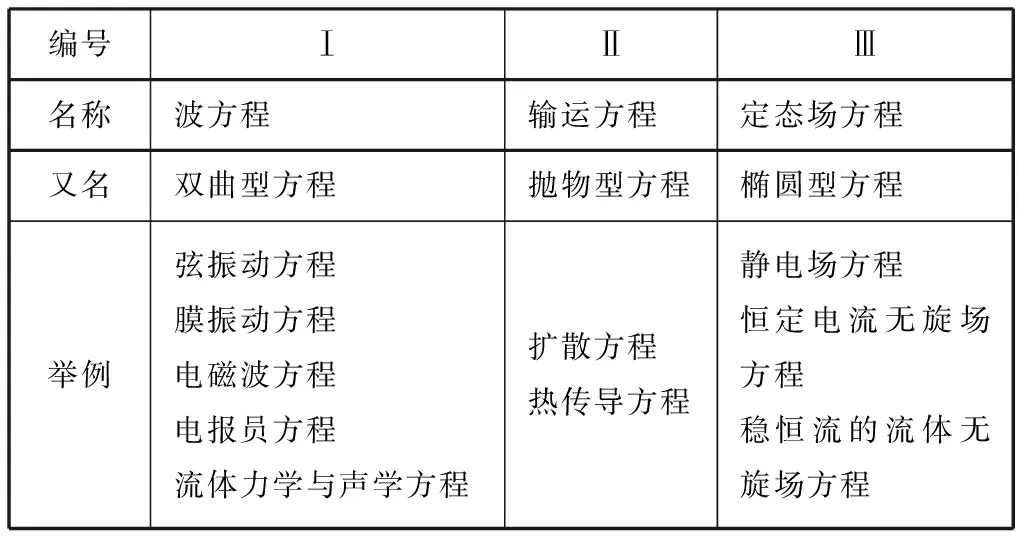
表1 经典数理方程的3种类型

杨新铁[2]指出，正是钱学森和von Karman把小扰动理论向非线性推进，采用虚拟气体假设从而改进了尺缩变换，导致跨声速时不出现质量密度无限大。高亚声速问题的可计算性强化了工程师们的信心——他们知道在β>1时要用双曲型变换作计算。出现奇点现象本质上是因为强非线性问题被当作小扰动线性方程求解问题；而物理学的SR与空气动力学中的可压缩性线化描述是一致的。为了借鉴空气动力学中的强非线性描述方式就得容许对SR添加一些高阶的非线性修正。在跨声速时从非线性观点看公式(2)要变号；即有

(3)

现在，我们有了两个密速公式；头一个是公式(2)，它适用于亚声速(vc，β>1)。但这两式均未避免奇点，即在正好为声速(v=c、β=1)时，密度为无限大。这个奇点的存在与实际不符，亦即风洞实验中从未发现密度超大的SSW。也就是说，飞机以声速飞行时并未遭遇无限大密度，飞机以超声速飞行时也没有遭遇过虚数密度。这就证明科技人员不能被某些数学公式吓住，而要重视物理实在。……1905年Einstein[3]的SR理论认为不可能超光速，后来被称为光障；但有许多研究却证明超光速现象存在[4-50]，道理是一样的。

在这里有必要指出，对宋健的话应有正确理解。虽然人类早已实现了超声速飞行，甚至进入了高超声速时代[52，53]；但在光的领域还差得很远。尽管超光速实验做了不少，但仍回答不了“未来的飞船能否在宇宙中以光速甚至超光速飞行”的问题，因此还要等待。

如果(3)式能用于跨声速时的计算，那么就有

(3a)

取ρ0/ρ=1/6，则有β≌1.01，即刚跨越声速(v比c仅大1%)。故宋健所述数据(ρ=6ρ0)是指早期情况，不是说一定是6倍。但无论如何在跨越声速时不会遇到无限大质量密度，激波现象并非不可克服。这样，在从技术上和工艺上设计超声速飞机之前，理论思想方面的障碍先行解除。表2是笔者搜集整理的飞行器超声速事例。

表2 飞行器超声速事例

在当前，Ma≥5的高超声速技术(hypersonic technology)是各国竞相研发的重点，中国也开展了积极的研究工作[52，53]。但这并非一个容易成功的方向，例如美国国防部高级研究项目局表示，高超声速武器的速度可高达20马赫。用超燃冲压发动机对武器进行10分钟的助推可以使它以最快速度飞行4000公里以上。即便是最先进的导弹防御系统也很难拦截如此高速移动的威胁。……当前的关键是发动机；超燃冲压发动机是一种吸气式发动机，要在速度达到5马赫或以上才具备运行条件。传统的喷气发动机无法经受超高速的冲击。超燃冲压发动机没有像涡轮风扇那样的可移动部件，而是利用飞机向前的运动来压缩空气，并将它与高能燃料混合，产生爆轰驱动力。与冲压发动机不同的是，超燃冲压发动机中的空气即便是经过压缩后其速度还是要快于声速。

中国科学院力学研究所在2020年5月宣布，为中国高超声速攻击武器打造的超燃冲压发动机能够在推力达到最大的情况下，至少运行10分钟，持续时长在全世界首屈一指。

3 非线性波动力学的发展

线性系统常用平滑函数表示，具有规则性，整体等于部分之和，服从叠加原理。非线性系统是初始状态变化不导致后续状态成比例变化的系统，表现为非规则，不可预测，整体不等于部分之和，叠加原理失效；而且初始状态的微小变化可能造成系统性质的运动结果的重大改变。在物理世界中，非线性作用有时会造成严重后果，因而必须躲避；但有时也有优势，例如线性行为表现为色散引起的波包扩散，而非线性过程却形成和维持空间规整性结构，例如孤立波(solitary waves)和孤立子(solitons)。孤子现象说明，非线性作用能造成突出的有序性——孤子在空间上局域、在时间上长寿，表现出奇怪的稳定性。

近年来非线性波传播很引人注意，这是由于在许多物理系统中其现象独特，也由于其处理使用了高深数学。在这里非线性Schrödinger方程(NLSE)具有基本的重要性，因为这是弱非线性状况下的色散波传播的普遍情状。……在20世纪后期，西方的有关论文常把两种现象分开，称之为波的shock和波的breaking，在这里我们译作“激荡”和“破裂”。这确实是非线性波传播的突出现象，而后者与前者密不可分，发生在前者的顶部超越底部时，与水波的破碎相似。

2016年，黄志洵[54]发表“非线性Schrödinger方程及量子非局域性”一文，指出Schrödinger方程(SE)是量子力学的基本方程，其地位相当于经典力学中的Newton方程。含时SE是波粒二象性的描写，说“SE只反映波动性”并不恰当。认为SE“只适用于低速情况”也是一种误解；SE不仅在用于原子、分子时极为成功，也被用在微波电子管技术中分析高速电子注，在光纤技术中分析光子的运动状态。SE是非相对论性方程，它的原始推导是从Newton力学观点出发的——取粒子动能Ek=mv2/2，其中质量m与速度v无关。尽管如此，用SE计算氢原子的双光子跃迁时仍有很高精确度。因此，SE的科学地位和历史地位至今无人能撼动。

SE是一个线性微分方程(LSE)，服从态叠加原理。在SE中加入非线性项，形成了非线性Schrödinger方程(NLSE)。在非线性与色散性共同作用下得到孤立波解，克服了SE的波包发散问题，开辟了更广大的应用前景。LSE和NLSE均为非相对论性量子波方程，本质上都反映由大量实验所证明其存在的量子非局域性。由于Schrödinger方程是非相对论方程的事实，造成了许多误解。例如有物理学家说，Schrödinger波动力学正确反映了低速微观现象的规律，为了反映高速微观物理现象就必须建立相对论性量子力学(RQM)。即要求把Schrödinger方程作相对论性推广，例如Klein-Gordon方程和Dirac方程就是如此。……这是似是而非的说法。关于SE的应用，对于自由粒子(如从某种源发射的自由电子)和非自由电子(如原子中的电子)当然不成问题。那么如电子作高速运动还能不能用SE?迄今没有理论或实验作出SE失效的证明。看看光子，它的运动速度为光速c，当然是“高速”了；那么SE能否用到光子上面？回答是肯定的。由于含时SE与Fresnel波方程相似，不舍时SE与Helmholtz方程相似，人们很早就用SE分析光波导，并取得了丰硕的成果。因此，认为SE只能在低速条件下使用的说法是错误的。

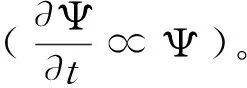
(4)

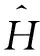
推导NLSE可以从非线性色散方程出发，采用Fourier变换法可推出变态NLSE[55]。在实系数条件下，如色散较强，可退化为标准型NLSE。这时可以用简单办法来辨识，即从式(4)出发，给Hamilton量加上非线性项，得到NLSE；取

(5)

(6)

式中β为非线性系数；故取U=0时，NLSE为

(7)

式中α=-ħ2/2m；在上式中，如取β=0则得线性方程LSE。

为作纯数学的讨论，把Ψ改写为代表函数的符号F，故得一维方程的写法为

(8)

这是标准型的实系数NLSE。上式具有复数解：

F=F0(z-vgt)ejθ

(9)

θ=θ(z-v0t)

(10)

式中vg、v0分别为包络速度和慢载波速度。

1973年V. Zaharov[56]证明有一种孤立波解：

(11)

式中

(12)

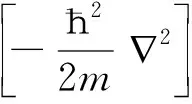
为了对照，看一下早期水面波理论中的KdV方程，因为其孤波解对应Schrödinger算符的束缚态。1834年，J.Russell[57]首先发现了水面上的孤立波现象，它在传播过程中波形保持不变，水体体积、波能量的绝大部分均集中在波峰附近。总之，孤立波是以单峰、匀速前进，在传输过程中保持形状、速度不变的一种行波，以单一实体出现并做局域分布。从数学上看，它是非线性方程的具有下述性质的解：①解的局部存在性质，即在一定范围内系统受扰动，与在整个空间分布的线性解不同；②解的几何形态(波形)保持不变；③两个(或多个)同样的波相遇时，由于非线性作用而互相作用，不是简单的线性叠加，并在后来又分开成为与相遇前相同的两个(或多个)波。

在孤立波分析中，齐次KdV方程(也叫浅水波方程)是十分重要的[58-60]。KdV方程与NLSE的求解有关，这是因为KdV方程的孤立波解对应Schrödinger算符的束缚态；而非线性方程的求解往往是化为线性方程的本征值求解问题。1895年，D.Korteweg和G.de Vries提出描写水面孤立波的方程(KdV方程)：

(13)

但(8)式可简化为

(8a)

另外，有所谓Hirota(广田)方程，其简化形式与NLSE十分相似：

(14)

取β=δ=1时就是NLSE。上述方程的共同特点是都有单孤子解。当然，在求解方法和物理意义的分析方面，相互参照比较都是有价值的。

(15)

解为

(16)

式中k为波数。可以证明相速vp=1-k2，群速vg=1-3k2；故波长不同的波，波数不同，vp、vg均不同。这是色散效应，是由∂3F/∂z3项引起的。另一方面，如忽略该项，有

(17)

解为

F=f[z-(1+F)t]

(18)

显然波速为(1+F)；故高幅区快过低幅区，传输过程中波形会变化(逐渐变陡直至破裂)。这是由非线性项引起的非线性效应。因此，KdV方程指出孤立波的形成是色散效应、非线性效应二者互相作用互相补偿的结果。

19世纪后期，法国数学家J.Poincarè(1854-1912)最先着手研究非线性常微分方程，以满足计算行星运动和稳定性的需要。自Poincarè以后的百多年，非线性科学有了巨大的发展。非线性方程的完全可积性，是说该方程描写的是多周期系统(Hamilton系统)。对于KdV方程的求解，当逆散射变换法成功实现后，就建立起KdV方程的Hamilton理论。关于NLS方程的求解，改进后的逆散射方法也获得成功，随之建立起NLSE的Hamilton理论。

1967年，Gordner等为求解KdV方程提出了逆散射变换法(C.Gordner，Phys Rev Lett.，1967，Vol.19，1905)。若前述初始条件及边界条件成立，可把KdV方程的解作为定态Schrödinger方程的势，则SE的散射量有确定的规律。这个定态位势方程有两类非平凡解，束缚态和散射态。……1968年，P.Lax[61]发展了逆散射变换法，将Schrödinger算子推广到一般非自伴算子，这种变换巧妙地把非线性问题转化为线性问题。下面是逆散射变换法的运作程序：①给定初值问题U1=U(k)，U(z，0)=U0(z)；②寻找算子H使U成为谱不变位势；③利用原问题写出H的散射量演化规律；④由U0(z)求出t=0时的散射量，并写出t时刻的散射量；⑤求解H的逆散射问题(t时刻)，确定位势U(z，t)。

总之，要正确估计SE成为非线性方程(NLSE)之后的变化和效果。NLSE的成功之处在于引入非线性项后在与色散效应的共同作用下得到了孤波解，不仅防止和克服了波包发散问题，而且使SE“不仅是一个波方程而且在本质上也是体现微观客体粒子性的方程”的内在逻辑自洽性得到加强。因此，NLSE开辟了更多的应用前景，例如它可用来处理激波问题。关于NLSE的一般理论可参阅文献[62]、[63]。

4 用NLSE分析声激波

由于用SE处理光纤取得完美成功，很容易让人以为NLSE只适用于分析LSW，而不适用于分析SSW。但这想法是错误的；2009年G.El等[64]证明了用NLSE处理SSW问题的可信性。

在可压流动力学中，激波的产生有两种情形。一种是当作理想流体动力学方程的初值问题的解；另一种发生在超声流通过一个物体时，是边值问题。有一种非线性波叫色散激波(DSW)，这与孤立子概念有关。文献[64]的题目是“2维超声NLS流通过一个伸展障碍物”，该文研究了一个细长宏观物体通过超流体(superfluid)的超声流，使用2维散焦NLSE。这问题的重要性相当于经典气体动力学的色散问题。分析时假定来流速度足够高，并与NLS船波(ship wave)进行比较，又参考了暗孤子(dark soliton)理论。分析中超声NLS流的Mach数达到10(Ma=10)，给出了形象化的彩色照片。该文的工作还可用于探索冷阱中超冷气体的行为，涉及用电场、磁场、光场去控制冷原子，具有较高价值。

(7a)

也就是

(7b)

此即[64]的公式(1)，是流体动力学中的多维NLSE；由于研究兴趣针对势流(无旋流)，可以写出

(19)

(20)

(21)

(22)

式中c是声速；由这些关系式，我们写出下述方程组：

(23)

(24)

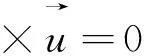
(25)

因此，文献[64]得到以下结果：①高超声速NLS流经过2维细长物体时必定伴随着两种DSW，它们具有不同特性；②超声速NLS流经过楔状物和细长翼时，可用色散近似构建精确的调制解；③当DSW发生于翼流中时，导出了描写调制解的精确方程；④得到了DSW背后的斜向暗孤子分布。

5 用NLSE分析光纤中的光激波

非线性光学(Nonlinear Optics)是近代光学的一个重要分支，最早是探讨在强激光光场作用下所发生的现象(见N.Blombergen[65]，1977)。2019年沈京玲[66]的著作《非线性光学基础和应用》有鲜明的特色，不仅在理论基础上阐述深刻，而且论述了太赫波(tera herz waves)产生、检测与应用中的非线性光学现象。……可惜这两种优秀著作都忽略了光纤中的非线性问题。光纤中是弱激光，但也有非线性现象。2006年，G.Agrawel[67]的专著《非线性纤维光学》出版，开辟了一个新方向，可看成非线性光学的一个分支。单模光纤中的光传播是研究NLSE的极好体系，这是由于可简化为1维平面波传播问题，而且光纤损耗极低。NLSE有两个物理效应：群速色散和自相位调制，并且有孤立波、频率chirping、光波breaking等现象。

光脉冲在光纤中传输时发生一系列非线性现象。可用NLSE很好地描述，尽管该方程仅包含两种物理效应——群速色散(GVD)和非线性自相调制(SPM)。在正常色散的波长范围中，这两者造成脉冲强势展宽，并向几乎为矩形的方向变形。……有关现象被称为光波破碎，与水波破碎相似。

1989年，J.Rothenberg[68]观测了光纤中光脉冲非线性传播形成的光激波，研制出可以模拟流体型DSW的测试平台。1992年，D.Anderson[69]论述了非线性光纤中波的破碎，分析了波破碎时色散与非线性的相互作用；他发现波破碎包含两个独立过程：脉冲不同部分的超越；相互作用时新频率由于非线性而诞生。该文的研究是在脉冲载频处于正常色散时进行的，结果与数据模拟吻合一致。另外，2008年M.Yavtushenko等讨论了在长周期或Bragg光纤中的情况，其时系统具有两个单向线性耦合波，对形成脉冲包络光激波的可能性作了研究。已经证实，从原理上讲，在非线性光纤中形成激波的可能性是存在的——不仅在波包的后缘，而且在波包的前沿。形成激波的原始态基本上取决于造成光纤激发的那些初始条件。在非线性光学中对DSW作了观测和研究，光被看成在光媒质中的理想流体，存在弱化的自散焦Kerr非线性。

2016年至2017年G.Xu等发表了两篇论文[70，71]；其一说以实验观测到色散性激波(DSW)；把一个短脉冲加到连续波之上，激波的固有振荡的可视性大为改善。其二是讨论“光子流体的色散性垮埧流动”，其中把光称为光子流体(photon fluid)；这些说法都启发我们大胆使用流体力学理论方法。2019年J.Nuno等[72]发表“光纤中的矢量化色散激波(VDSW)”，指出DSW是在许多科学领域都会遇到的普遍现象，包括流体动力学、凝聚态物理、地球物理学等。已经确定，光学在光媒质中的传播时表现为完美的流体，显示出微弱的自散焦非线性(self-defocusing nonlinerity)。对于DSW，这种类比变得有吸引力。在这里，观察到非线性光纤中一类新型的VDSW，类似于非粘性理想流体中的爆炸波(blast waves)。由正交极化pump脉冲产生的非均匀双活塞经由非线性交叉调相非线性相位势压印在一个连续波探头上而触发了VDSW，该调相是由正交极化pump脉冲产生的。探头上的非线性相位势导致形成零强度扩展区，而该区被两个互斥的振荡波前环绕。

矢量化DSW的工作机制为，设有一正常色散光纤，向其输入两信号，一是较弱的连续波探束，二是正交极化的短脉冲(SOP)。前者为u(z，t)，后者为v(z，t)，z是光纤传输方向。它们可用一组(两个)互相耦合的NLSE描写。对长度为公里级的光纤而言，可用Manakov模型：

式中γ是光纤的非线性Kerr参数，β是群速色散系数，α代表传输损耗。上式表明两个波仅由一个相位项而耦合。

Nuno所用活塞pump波(SOP)的参数为：波长1550nm，峰功率1.5W，脉宽41ps；连续波功率5mW；这些是实验所用参数。对上述方程作数值模拟，可算出一些图形。建立的实验系统用70GHz取样示波器和光谱分析仪进行观测。

6 未来宇宙飞船以近光速航行时的光激波

早期的飞机速度慢，涉及空气动力学的难题不多。但在飞机发动机不断改进、速度不断提高时，理论上遇到了许多问题。特别是SSW带来的飞行阻力增大，飞机表面温度急剧升高，一度使人们以为声速(约300m/s)是航空器速度的极限。但在上世纪30年代至40年代，科学家和工程师们协力攻关，1947年克服了声障。现在飞机以超声速飞行已不成问题，用高超声速(Ma≥5)才是难题。……那么，我们怎样考虑和估计宇宙飞船的未来发展？

尽管光障问题比声障问题复杂，其原理却很相似。基础数理方程揭示了自然规律的普遍性，声学、光学两大领域之间的联系是密切的。2019年笔者曾发表一篇文章“突破声障与突破光障的比较研究”[50]；本文并非对该文的重复，而是从激波这个论题切入，作更深刻的分析。进一步，2020年笔者又发表了另一文章“速度研究的科学意义”[73]，不仅作了分析而且给出了许多数据。该文表1是“人造飞行器所达到的高速度”，其中的数据表明，在2004年到2014年间，美国宇航局(NASA)达到的记录是17km/s至18km/s。2018年的新闻报道说，有一个太阳探测器达到了极高的水平，v=194km/s。即使这一数据属实，离光速(c=299792458m/s≌3×105km/s)还差得很远。

那么宇宙中有没有以超光速运动的天体？也许有。中国天体物理学家曹盛林教授一直持此观点，至今未变。1988年至1993年，他在《Astrophys & Space Sci.》杂志上发表5篇英文论文[9-13]，阐述这一问题。2019年曹盛林[74]出版了一本高级科普书《超光速》，更清晰地陈述了与此有关的观点。他指出，20世纪60年代末射电天文学家用甚长基线干涉仪(VLBI)发现，一些类星体射电源的两个子源以超光速分离，涉及天体有3c120、3c345、3c273等。另外，1994年天文学家观测到一个以超光速膨胀的天体，是在银河系内，这有照片为证。90年代起由Hubble望远镜的长期观测，也证明银河系内有超巨星以超光速膨胀；2002年的巨星膨胀，其速度v=4.3c。

因此，尽管实现由人类建造超光速宇宙飞船的设想还十分遥远，但有必要考虑在宇宙中的物体(天体或飞船)若以近光速飞行，是否会有LSW现象？物理真空作为一种媒质有否可能生成激波层？……我们也可以换一种方式提问：在高能物理实验室中，在加速器或对撞机里，当粒子(电子或质子)以近于光速c的速度飞行，它们是完全无所阻碍还是也会遇到波阻问题?

我们必须作逻辑性的思考。首先，光激波(LSW)的存在是事实，它已在光纤等物质中观察到，并发展出完善的理论。但这是固体物质，虽已推广到气体，但“在真空中高速飞行的物体也会产生LSW”的报道从未出现过。光在光学媒质中传播时表现为完美的流体，因此用得上流体力学方法。那么光在真空媒质中传播时是否也会如此？我们希望是，这样可与把光称为“光子流体”的思路相吻合。……问题是怎样看待光在真空中的传播?

直到19世纪中叶，人们都认为没有“不要媒质也能传送”的波动。因此，既然光是波动，而且能在真空中传播(由太阳光可射到地球而证明)，那么一定有一种光媒质存在。它可以是看不见的，但弥漫于宇宙之中，物理学家称之为ether(以太)。科学界一度热衷于做证明以太存在的实验。一般认为以太是绝对静止的，而地球相对以太的速度就是地球绕太阳的公转速度。在参考了地球绕日公转速度后，人们得出下述看法，即光顺以太和逆以太运动时速度不同(确切说将有2.15×10-4的差异)。1887年，A.Michelson和E.Morley所做的精确实验否定了以太存在[75]。1926-1928年间，70多岁的Michelson再作努力以实验寻找以太漂移，仍以否定告终。但是，他从未宣布过他放弃了以太，他对狭义相对论(SR)也持有一定程度的保留。……

SR时空观与Galilei、Newton以及Lorentz时空观的根本区别在于SR时空观的相对性。H. Lorentz[76]的科学工作是近代物理学的基石；我们知道，现有的推导Lorentz变换(LT)的方法有多种；而写入大学教材的推导方式常常有个前提——不同参考系测得的光速相同。或者说，LT是由相对性原理和光速不变原理导出的，由此出现了尺缩、时延现象。1904年时的Lorentz信奉以太论和绝对参考系，在此信念下导出的LT被SR继承和应用，而SR却不承认绝对参考系。

然而近年来国内外多位科学家提出存在优先参考系(prefered frame)，即有绝对坐标系的形成。故Lorentz-Poincarè时空观重新受到重视，亦出现了进一步的理论。多年前科学刊物《New Scientist》所报道的“以太论高调复出”，提醒我们不宜完全抛弃SR出现之前的科学成果。如果说现在有向Galilei、Newton、Lorentz回归的倾向，那也是在现代条件下的高层次回归，而不是简单的倒退。

Lorentz物理思想重新受到重视是有原因的。1977年Smoot等[77]报告说，已测到地球相对于微波背景辐射(CMB)的速度为390km/s；因而物理学大师P. Dirac[78]说，从某种意义上讲Lorentz正确而Einstein是错的。美国物理学家T. Flandern[20]于1997年—1998年间发表引力传播速度(the speed of gravity)为v≥(109～2×1010)c，同时他声称用Lorentz相对原理(Lorentzian relativity)就能解释这些结果，而SR在超光速引力速度面前却无能为力。

关于存在绝对坐标系(亦即优先的参考系)的见解已是大量存在；这与1965年发现微波背景辐射有关，也与1982年法国物理学冢A.Aspect[79]完成的量子力学(QM)实验有关。大家知道自1935年Einstein[80]发表EPR论文之后，对新生的QM究竟如何看待引起很大争论。1965年提出著名的不等式的J.Bell在1985年说[81，82]，Bell不等式是分析EPR推论的产物，而Aspect实验证明了Einstein的世界观站不住脚。这时提问者说，Bell不等式以客观实在性和局域性(不可分性)为前提，后者表示没有超光速传递的信号。在Aspect实验成功后，必须抛弃二者之一，该怎么办呢？这时Bell说，这是一种进退两难的处境，最简单的办法是回到Einstein之前，即回到Lorentz和Poincarè，他们认为存在的以太是一种特惠的(优先的)参照系。可以想象这种参照系存在，在其中事物可以比光快。有许多问题通过设想存在以太可容易地解决。在发表了这些惊人的观点后，Bell重复说：“我想回到以太概念，因为EPR中有这种启示，即景象背后有某种东西比光快。实际上，给量子理论造成重重困难的正是Einstein的相对论”(着重号为笔者所加)。

如果我们认为Lorentz坚持以太论正确，而今天又不能简单地回到19世纪的思想，就必须回答一个问题：什么是新以太？旧以太(经典物理中的以太)被认为是绝对静止的，这个MM实验的前提并不恰当，“未发现绝对静止的以太”和“不存在以太”不是一回事；新以太应当能够担起绝对参考系的重任。

笔者认为，这个新以太就是物理真空(phisical vacuum)，也叫量子真空(quantum vacuum)。支持这一观点的是一个新证据，表明其中的仅为短暂出现的虚光子和普通光子一样可以产生物理作用——2011年西班牙科学家发现在已实现工程真空的环境中的旋转体(直径100nm的石墨粒子)会减速，表示真空也有摩擦。环境温度越高虚光子越多，减速作用就越显著。可见，李政道教授所说(“真空很复杂，它是有结构的”)完全正确。这就是人们寻找了百多年的“(新)以太”!

正如飞机在空气中运动时若速度很快就有SSW，飞船在宇宙中运动时若速度很快也会有光激波(LSW)。可以推断，后者在所谓奇点(v=c，β=1)并不会出现无限大密度、质量和能量。“真空光激波”(LSW in vacuum)如存在，不会对飞船加速到光速以上(v>c)构成障碍。

7 未来宇宙飞船以超光速航行的可能性

可以把真空看成一种特殊的介质(媒质)，这个观点己被某些国外的独特研究所验证。把真空当作媒质，那么就可以研究它的折射率。1990年K.Schanhorst[14]发表论文“双金属板之间的真空中光传播”。所分析的是Casmir效应结构——两块靠得很近的金属平板；这是把一定的边界条件强加到光子真空涨落上。Schanhorst用量子电动力学(QED)方法进行计算，得到垂直于板面方向的折射率np(下标p代表perpendicular)比1略小；根据公式vp=c/np，算出相速比光速略大(vp>c)。在频率不高条件下讨论，可以忽略色散，群速等于相速，故群速也比光速略大(vg>c)。显然，这项研究是把真空当作介质(媒质)来看待的。

因此很明显，“光波可经过真空传播”并不意味着“光的传播不需要介质(媒质)”，而是说光传播要仰赖于“新以太”，即具有量子特性的物理真空媒质。经典物理中真空的折射率等于1，量子物理中真空的折射率比1略小。

基础理论概念清晰化以后，还有一个问题有待解决，即飞船在宇宙深空中以超光速航行所用的模式。笔者认为中国科学家已作出了简明扼要的回答，那就是自主惯性导航的飞行模式。……2004年11月26日至28日，在北京香山召开了“香山科学会议第242次学术研讨会”，本次会议由宋健院士建议和领导，主题为“宇航科学前沿与光障问题”(Frontier Issues on Astronautics and Light Barrier)。会议主题评述报告为宋健院士所作(“航天、宇航和光障”)，宋健[51]指出，飞出太阳系是人类的伟大理想，这里有许多理论和技术问题要解决，科学界已开始考虑和工作。至于进入银河系，必须加大航行速度，直到接近光速，可能的话应超过光速。目前航天技术已开始放弃狭义相对论的技术基础，即从用电磁波双向时间间隔之半作为距离定义，改由卫星和飞船上用编码报文形式向地面单向传送所有信息；飞船上独立自主的计量、观测、导航和发讯都与地面观测无关。至于Einstein说的“不可能存在超光速运动”，那只是猜测，没有实验根据，也不是科学定律……。他又说：“如果从40年航天技术实践反过来检查SR的计算结果，就会发现即使在远低于光速的情况下，自主导航的工程实践与SR动力学也发生冲突。例如，发动机推力依赖其惯性速度的现象就从未发现过。半个多世纪的航天技术实践都证明至少在第三宇宙速度(v3=16.6km/s)左右，齐奥尔科夫斯基公式是足够准确的，从未发现过推力依赖于速度的情况，无论是飞船上和火箭上用加速表自主测量和地面光测、雷测都证明了这一点。人们常说，只有v接近c时才会发生。那也要有实验证明才能作为解决技术问题的基础。所以利用狭义相对论动力学公式去计算航天器飞行速度要十分谨慎。……”(着重号为笔者所加)。

另一个中心议题报告为林金院士所作(“宇航中时间的定义与测量机制和超光速运动”)[83]。林金就自主惯性导航提供一个新理论模型，用来分析处理惯性导航的时间定义、测量机制和超光速运动。他认为，一个运动质点自己可以测量自己相对一个给定惯性系的位置、速度和加速度，作为质点自带的运动钟固有时间的函数。原理上不需要与外界交换信息，不存在任何信号传递的速度问题。自主惯性导航是基于引力场的性质，即使这个世界没有电磁场、没有光，纯惯性系统照样工作，照常自主定位、测速；既如此，3×108m/s为何会成为速度的极限？简言之，惯性导航的宇宙飞船的时间定义即飞船运动钟固有时间；只要未来能开发出新型动力源，飞船的速度不存在上限。……林金还认为，应恢复光子和其他微观粒子相同的普通地位，即有静止质量，其速度也不是极限速度。

笔者认为，在回顾林金的论述时，不妨再看看1905年Einstein对“同时性”的概念怎么说。Einstein写道[3]：“我们应当考虑到：凡是时间在里面起作用的我们的一切判断，总是关于同时的事件的判断。比如我说，‘那列火车7点钟到达这里”，这大概是说：我的表的短针指到7同火车的到达是同时的事件。可能有人认为，用‘我的表的短针的位置’来代替‘时间’，也许就有可能克服由于定义‘时间’而带来的一切困难。事实上，如果问题只是在于为这只表所在的地一点来定义一种时间，那么这样一种定义就已经足够了；但是如果问题是要把发生在不同地点的一系列事件在时间上联系起来，或者说——其结果依然一样——要定出那些在远离这只表的地点所发生的事件的时间，那么这样的定义就不够了。”

在这里，Einstein是说用一只表定义时间的不可能性。然而，正如林金所指出的，今天的纯惯性导航只用“一只表”的固有时间，是完全自主的，不需要辐射或接收任何光(电磁)信号和外界发生联系，所以测量机理十分简单。设想一艘配备有惯性导航仪器的宇宙飞船，飞船相对惯性坐标系(Galilei参考系)作加速飞行。只要积分的时间足够长，飞船相对惯性系的飞行速度(加速度表输出脉冲总数)可以超过3×108m/s。无须设想恒定或随时间变化的引力场，宇航员观察惯性仪表的指示，进行完全自主式的宇宙航行。加速度表先在静止在地面(发射点)的引力场中标定，在飞行中测量火箭推力产生的惯性加速度。加速度表静止在地面实验室做寿命试验，等效于加速度表在没有引力场的宇宙空间做1g的恒加速飞行试验。由于

(28)

故大约1年后飞船速度超过3×108m/s，即以超光速航行。

因此，宋健、林金两位航天专家不仅赋予超光速研究明确的目标和意义，而且深刻地对主流物理界的“光障理论”作了批评。更重要的是，他们用自主惯性导航分析处理超光速运动取得成功。这些珍贵的精神遗产值得后人作进一步研究。

8 结束语

物理学中的不同学科常有类似和相同的规律。例如在数理方程的3种类型中，双曲型偏微分方程蕴含了力学、电磁学、光学、声学及热传学核心内容。在科学探讨中作比较研究不仅可行，而且非常重要。尽管声波速度与光波速度在数值上相差很大，但从数学和物理上对突破声障与突破光障比较研究仍有特殊意义。自然规律的普适性使不同学科之间产生联系并使相互借鉴成为可能。对激波的研究也如此，以NLSE为基础的数学分析使我们对SSW和LSW的认识达到了新的高度。本文的分析也证明了波科学(science of waves)的普遍意义和重要性。

从20世纪30年代开始，到本世纪的头20年，航空及航天工程技术的迅猛发展给了我们有益的启示。它们已彰显出当今的两大研究领域——高超声速技术和超光速探索。但两者都非常艰难，成为在21世纪对人类智慧的挑战。……声激波和光激波的研究，给我们提供了另一个视角，也使数学方法得到发展。有关物理现象既丰富，又令人感兴趣。虽然本文对SSW和LSW作了深入分析，又对未来的飞船在宇宙深空航行时的情况作了初步讨论和估计；但仍有许多不清楚的问题，期待更多的人参加研究。

致谢：本文在写作时得到杨新铁教授、姜荣讲师及王雨女士的协助，谨致谢意！