以问题导向构建学习型课堂

简树恩

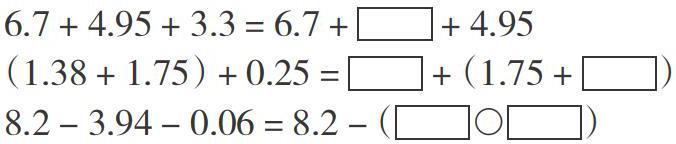
摘 要：问题化学习强调持续的学习行为，通过系列化问题的提出、思考与解决，促进学习的有效迁移，实现知识的连续建构，即围绕问题的学习是一种无处不在的连贯状态。简单地说，问题化学习就是通过问题来建构自主学习过程的活动，它要求学习活动以问题的发现与提出为开端，用问题主线来贯穿学习过程和整合各种知识，并把对问题的思考、解决、感悟，作为对学习目标的追求与对学习结果的检验。实施问题化学习的课堂，有利于培养和发展学生的数学思维，让学习真正发生在自我需要的层面上。

关键词：小学数学;问题导向;学习型课堂

笔者以人教版小学数学四年级下册“整数加法运算定律推广到小数”一课为例，以通过回答三个问题的方式，谈谈实施问题导向，建构学习型课堂策略。

一、一节课的核心问题是什么

核心问题主要对应教学内容的知识点与技能点。把握教学内容中隐藏的核心问题是形成教与学导向的关键。如何准确把握？主要落实两个方面：教材研读与学情考虑。

首先，作为教师要研读《教师教学用书》，认真领会编者意图与教学建议，再结合新课标的学段目标考虑（“初步形成数感”“在观察、实验、猜想、验证等活动中，发展合情推理能力”“会独立思考，体会一些数学基本思想”），然后充分考虑四年级学生的学情，这样确定的核心问题就会比较准确，比如本课的核心问题可以定为：你认为整数加法运算定律可以在其他数上应用吗？

二、为什么把它作为核心问题

当教师界定核心问题后，要通过两个方面仔细推敲，辩证选择的准确性。

第一，教材的编排和意图。首先清晰定位知识能确定教学的起点，本内容是全册教材里小数加减法的最后一部分内容，安排在三年级下册学习了“小数的初步认识”，四年级下册整数的“四则运算”“整数加法的运算定律、减法的性质和简便运算”，以及在“小数的加法、减法和加减混合运算”的基础上，接着考虑下位知识，为后续五年级上册学习“小数乘除法”后，将整数乘法的运算定律推广到小数;下册学习“分数加减法”后，将整数加法运算定律推广到分数;还有六年级上册学习“分数乘除法”后，将整数乘法的运算定律推广到分数提供基础。综合对上下位知识的考虑，可以确定核心问题的定位是适合逐步拓展运算定律的使用范围，最后完成运算定律推广的全过程。核心问题以“推广”作为重心，可以说是做到为整个知识体系的建构而教。

第二，重视对学情的关注。知识基础：在此之前学生已掌握整数的四则运算的意义和关系，整数加法的运算定律、减法的性质，并能应用运算定律进行整数简便运算，还会计算“小数的加减法以及加减混合运算”。年龄特征：四年级的学生已初步具备独立解决问题的能力，希望通过自己的努力来证明自己的见解，获得认同。从学生的已有知识、数学学习经验、年龄特征等因素综合考虑，提出了具有探究意义、能激发学习动机的核心问题。这一核心问题的确定和导向，也充分体现了研学后教课堂教学改革所倡导的“让问题成为中心”的核心理念。

三、围绕核心问题，如何展开教学流程

为了达成核心问题的有效落实，选用合适的教学方法组织教学至关重要。围绕核心问题，可以选择以下三种教学方法。第一，启发教学法。启发学生关注“整数加法运算定律是否可以推广到其他数”的思考。第二，探究实验法。根据对问题的猜想，大胆开展探究实验。第三，谈话讨论法。经过独立或合作验证猜想的过程后，最需要做的就是围绕核心问题进行讨论、汇报，并总结概括。设计的教学流程分为四个环节：回忆定律、迁移定律、应用定律和拓展延伸。

（一）回忆定律

1. 想一想

师：我们学习了有关整数加法的运算定律，能说出一条定律并用字母表示的请举手？两条的？三条？

小学数学是系统性很强的学科，每项新知识往往是旧知识的延伸和发展。我们要从学生的已有经验出发，把握知识的生长点。在“回忆定律”这个部分，设计了两个层次活动。通过回忆、思考学过的整数加法的运算定律，一方面，学生了解自己的掌握情况，另一方面，教师也了解学生的学习现状，并有效地根据学情灵活调整教学，抓准教学起点。

2. 写一写

说是为了能写，能独立地写，才能开展有效的独立学习。

a+b=b+a    a+b+c=a+（b+c）

a-b-c=a-（b+c）   12+35=35+12

86+25+75=86+（25+75）

193-46-54=193-（46+54）

通过想一想、写一写两个活动，引导学生回顾整数加法的运算定律，充分调动学生已有的认知经验，关注学习的起点。这样的学更积极主动，这样的教更为有效和富有针对性。

（二）迁移定律

认知结构迁移理论认为：一切有意义的学习必然包括迁移，迁移是以认知结构为中介进行的。通过上一环节对学生原有知识经验的提取，找到了知识的生长点，本环节将引导学生经历“猜想——验证——建模”全过程，将整数加法运算定律迁移到小数。

我们所学的加法交换律、结合律和减法性质，只是用在整数的计算当中，“你认为整数加法运算定律可以推广到其他数吗？”

核心问题由此抛出，意味着“猜想”的开始，而问题的清晰指向，学生定能及时思考：可以推广到哪些数呢？由于刚学过小数，所以猜想“小数”是顺理成章的回答，相信不乏學生会猜想到“分数”，教师可更好地为知识系统做准备。假如学生没有想到分数，也可以在课的结束时作延伸。猜想是为了有研究的方向，有了目标，就能有目标导向，激发起探究的欲望，也带出“验证”的需要。

整数加法运算定律能否推广到小数呢？请你举出例子验证自己的猜想。可独立完成，也可合作完成。

验证的活动需要学生独立完成，以体现自我举例、自主探究、独立验证的问题研究方式，让学生真正成为学习的主人，亲身经历知识迁移和形成的全过程。

猜想、验证、总结是问题探究式学习的完整过程，学生经过猜想确定研究方向，通过验证证实猜想，依靠总结经验来提升整个研究过程，最后的汇报交流环节是重点，是使学生形成共识的建模过程。这过程可以将不同例子逐一投影，并汇报验证的结果，通过不完全归纳的推理过程，使学生体会这一结论的普遍意义，完善对加法运算定律的认知，最后达成共识，学会将整数加法运算定律推广到小数，从而完成核心问题的解决。

（三）运用定律

练习是掌握知识、形成技能、发展思维的重要环节。本课可以设计三个不同层次的练习，以达到反馈新知掌握情况，深化理解和拓展延伸的功效。

1. 基础练习，形成技能

（1）巧填算式

这道练习增加了减法的性质，进一步加深对加法运算定律的理解，为下面的简算作好铺垫。

（2）怎样简便怎样算

1.88+2.3+3.7 13.7+0.98+0.02+4.3

5.17-1.8-3.2 4.02-3.5+0.98

考虑到学生的认知规律应是由易到难，循序渐进的，教师可调整教材练习顺序。在这里，重点让学生说清为什么这样算，依据是什么，从而加深对定律的理解和应用，还引导学生对比不同的算法，进一步优化算法，提高运算能力。

2. 对比练习，克服负迁移

通过基础练习，学生对运用定律进行简算积累了一定的经验，为克服负迁移的影响，笔者设计了一组对比练习。

计算下面各题。

2.97+1.86+0.03 2.97+1.86+0.3

小数的末尾同样有7和3，为什么做法却不同？

通过强烈的对比，在培养数感的同时，使学生明白，计算前要注意观察数据的特点，做到具体问题具体分析，灵活计算。

3. 拓展练习，灵活应用

（1）选数，写算式

选择你喜欢的几个数，编一道能用简便方法的算式。

5.1   0.5   3.9   7.12   2.5   2.88   4.3

这是一道开放性的练习，答案并不唯一。学生要编题，首先要懂得根据数据特征选对数，再就是要充分理解加法定律，接着通过当小老师检查同桌的对错，营造了学生教学生的学习氛围，进一步加深对知识的内化。

（2）小数据，大道理

小兰买了9颗不同价钱的糖，算一算，她一共花了多少元？

0.1+0.2+0.3+0.4+0.5+0.6+0.7+0.8+0.9=？

最后，以解决生活问题为背景，让学生体验数学的应用价值。探索求连续的9个小数的和，看似简单，其实渗透着等差数列求和的方法。

三个不同层次的练习，由浅入深，体现梯度，使不同程度的学生都有发展。这是新课程倡导的让不同层次的学生在数学学习上获得不同的发展。

（四）拓展延伸

师：以前我们认为运算定律的abc代表的只是整数，今天发现它还可以表示小数，那也许它还可以表示……

一句话的延伸，所蕴含的深意是对整个知识结构的系统构建，真正为后续的学习指明了方向，也为学有余力的学生提供继续自我追求的机会。

回顾核心问题，拓展并渗透运算定律的使用范围，为的是整个知识结构而教。根据问题导向设计课堂，充分凸显以學生为主体的教学理念，通过长时间的探索与实践，笔者发现：问题导向式课堂有助于知识的整体建构，使学生在各类知识的学习上均能以解决问题的方式展开，提高提出问题、分析问题、解决问题的综合能力。同时，以问题导向式课堂的实施可以提高教师对教材的解析能力，对课堂教学的组织能力，从而有效促进教师的专业发展。