梁的挠度和转角问题分析
2020-04-18 06:17焦之森
科学技术创新 2020年6期
王 爽 焦之森
(齐齐哈尔大学建筑与土木工程学院,黑龙江 齐齐哈尔161000)
对简支梁、外伸梁的变形问题的解析计算方法有很多种,常见的有积分法[1-5]、能量法[1-5]、叠加法[1-5]、奇异函数法[1-5]和共轭梁法[1-5]等,在用积分法求解简支梁、外伸梁的变形问题时须求解多个积分常数,计算繁琐;奇异函数法仍属于积分法,求解过程也须解积分常数;如果仅计算某一截面的位移,能量法较为简单,不过仍须进行积分计算[6]。本文通过间接叠加法,来介绍简支梁、外伸梁等结构在受载荷作用时挠度及转角问题的简单求解方法,即将简支梁、外伸梁等结构在受载荷作用时挠度及转角问题,转化为有初始转角的悬臂梁受载荷时的变形问题,使简支梁、外伸梁等结构在受载荷作用时挠度及转角问题的求解过程的思维难度得到很大程度的降低,从而问题变得更容易理解。
1 原理介绍与例题分析
悬臂梁具有一个固定端,当悬臂梁受已经与水平线外荷载作用时,靠近固定端的载面不发生转动,转角为零。如果有一个悬臂梁,在未荷载时,形成一个小的角度θB,如图1 所示。
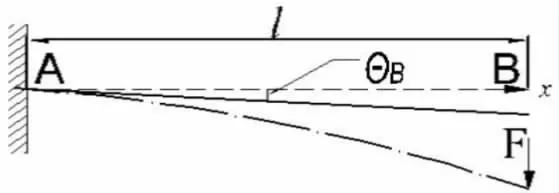
图1 有初始转角的悬臂梁
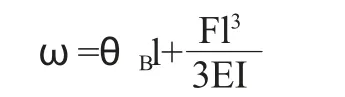

例2-1 一端受集中力偶的简支梁
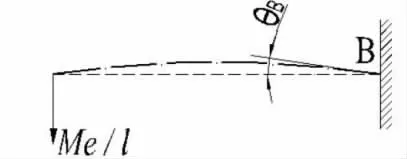
例2-2 等价后的有初始转角的悬臂梁
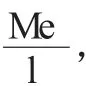
例2.如图例3-1 所示,求截面转角及跨中挠度。
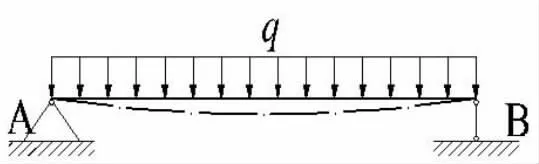
例3-1 作用均布载荷的简支梁
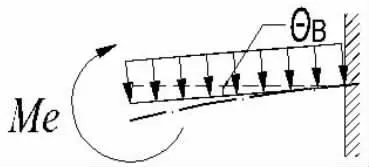
例3-2 等价后有初始转角的悬臂梁受力图
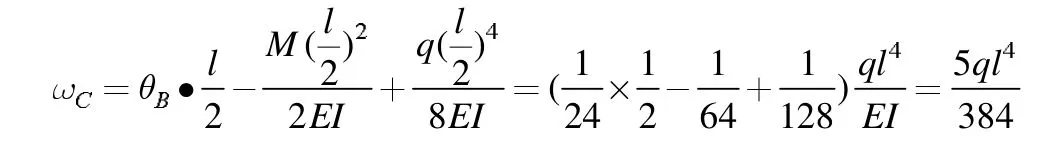
例3.如图例4-1,求外伸梁C 端挠度。
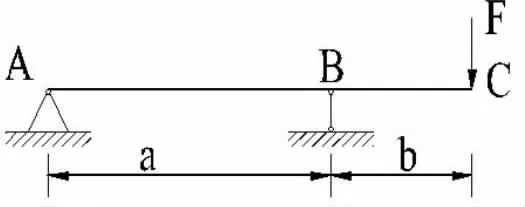
例4-1 作用集中力的悬臂梁

例4-2 作用均布载荷的简支梁

例4-3 等价后有初始转角的悬臂梁
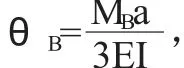
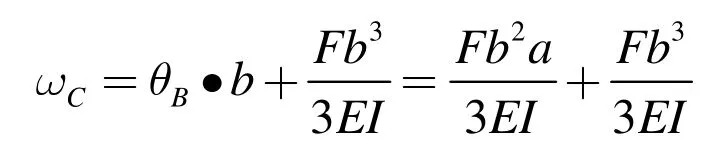
2 结论
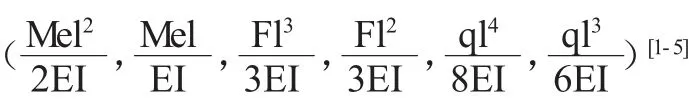
猜你喜欢
运输经理世界(2022年2期)2022-09-22
小朋友·快乐手工(2018年7期)2018-08-15
小朋友·快乐手工(2018年7期)2018-08-15
现代职业教育·中职中专(2018年11期)2018-06-11
课程教育研究·新教师教学(2015年12期)2017-09-27
新课程·上旬(2017年8期)2017-09-24
山东工业技术(2016年15期)2016-12-01
小朋友·快乐手工(2016年7期)2016-05-14
建筑工程技术与设计(2015年20期)2015-10-21
建筑工程技术与设计(2015年27期)2015-10-21

