转子Halbach多极环与表贴式对电机转矩分析比较
孙贤备,陈进华,魏梦飞,张 驰,杨桂林
(中国科学院宁波材料技术与工程研究所,浙江 宁波 315201)
0 引 言
机器人关节正朝轻量化、柔顺化方向发展,这也决定了机器人关节电机朝高转矩密度,低转矩波动方向发展。目前关节电机多采用体积小、重量轻、结构紧凑的无框力矩永磁电机。电机永磁体的安装排列设计灵活多样,目前市场上的无框电机多采用普通的表贴式磁极结构[1-2]。但是表贴式结构转子磁极间过渡区大,且动平衡差,在高速情况下不加保护套,磁极有甩出去的风险。而加碳纤维、不锈钢等保护套会增加气隙尺寸,降低电机性能。
Halbach永磁阵列具有正弦和磁屏蔽等特点,在永磁同步电机中的应用越来越广泛。同时Halbach永磁阵列可以提供较大的气隙磁通密度基波幅值和较低的气隙磁通密度谐波畸变率,显著提高永磁电机功率密度、降低转矩波动,同时减小了谐波损耗,因而可以优先使用于无框力矩永磁电机[3-7]。
Halbach永磁阵列有两种充磁方式:分段充磁和连续充磁。工程中应用较多的是分段充磁[8-12],即每个磁极分为若干段,每段永磁体充磁方向按照一定的规律周期性变化。但是这种充磁方式引起的气隙磁场含有大量的谐波,降低了电机的转矩密度并增加转矩波动,伴随有振动和噪声。而连续充磁的Halbach永磁阵列产生的气隙磁密波形为理想的正弦波,其每个磁极可视为分为无数段,每段永磁体充磁方向连续变化[13]。该种阵列的电机具有高转矩密度和低转矩波动。利用该种充磁方法可制作Halbach结构多极磁环。
本文以一台18槽无框力矩永磁电机为研究对象,首先在该电机转子使用Halbach结构多极环的情况下,建立无槽定子空载气隙磁场解析模型[14]。其次,对电机转子采用表贴式结构和Halbach结构两种方式。对表贴式结构,主要对永磁体外圆弧半径大小进行参数化仿真以减小齿槽转矩;对Halbach结构,建立无槽定子仿真模型[15],利用有限元法验证解析法的正确性。利用有限元法建模仿真,分别从转子磁轭厚度、气隙磁密大小及T-I曲线三方面比较两种结构转子电机的性能。最后,通过样机实验,分析比较两种转子结构的电机性能,选出最佳的转子结构。
1 Halbach结构多极磁环分析
整体磁环按取向来分类,可分为辐射取向和极取向。极取向磁环又称Halbach结构多极磁环,是目前磁环中磁性能最高的一种,可用烧结方式制造。Halbach结构多极取向磁环可分为外向聚磁型和内向聚磁型。所谓外向聚磁型,即永磁体阵列外部的磁场得到增强并呈现类正弦性,适用于内转子电机;内向聚磁型,即永磁体阵列内部的磁场得到增强并呈现类正弦性,适用于外转子电机。
Halbach阵列原理是将不同冲磁方向的磁铁按一定规律排列,使气隙磁场可以按照正弦分布。第i块永磁体的充磁方式θmi由下式决定:
θmi=(1±p)θi
(1)
式中,p为极对数,“+”、“-”分别对应外转子和内转子结构,θi为第i块永磁体中心线与θ=0之间的夹角(如图1所示)。
(2)
式中,l为每极磁块数。
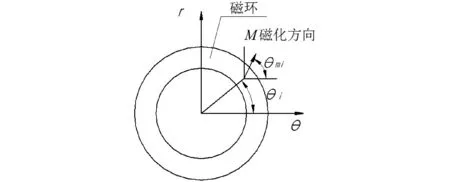
图1 M磁化方向图
在极坐标下,磁矢量分布为
M=Mrer+Mθeθ
(3)
式中,Mr=Mcos(pθ),Mθ=±Msin(pθ),M为磁化矢量。
分段式Halbach阵列组成的内转子电机磁场简化后模型的气隙磁密表达式如下[14]:
(4)
(5)
(6)
式中,R0为定子内圆半径,Rmo为磁环外圆半径,Rmi为磁环内圆半径,μ0为空气磁导率,r为所计算气隙磁密点距离圆心的距离。
Halbach结构整体环可以看成由无穷个永磁体按一定规律排列而成,即l=∞,则式(6)变为
(7)
2 两种转子结构建模分析
本文利用Ansoft maxwell有限元软件对表贴式、Halbach结构多极环两种转子结构进行建模仿真(见图2),比较两种转子结构的电机性能。
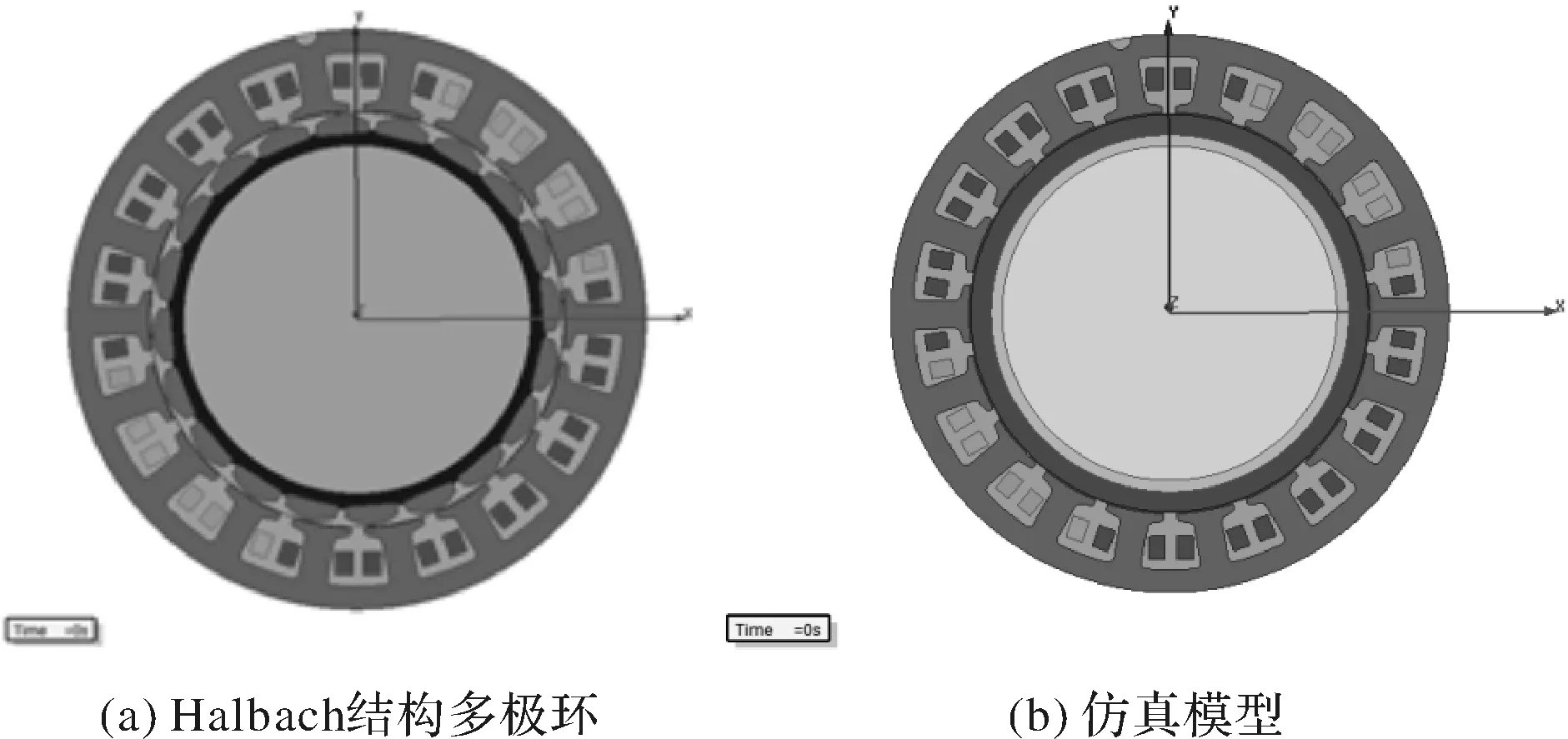
图2 表贴式
2.1 表贴式磁钢的优化
针对表贴式转子,改变永磁体外圆弧半径大小,改变气隙磁密分布,影响齿槽转矩。在Ansoft maxwell软件中,以永磁体外圆弧半径R为参数(如图3所示),进行参数化扫描仿真,得到齿槽转矩随永磁体外圆弧半径的变化曲线图(如图4所示),电机线反电势幅值随永磁体外圆弧半径的变化曲线图(如图5所示)。

图3 表贴式转子

图4 齿槽转矩随永磁体外圆变化图

图5 反电势幅值随永磁体外圆变化图
齿槽转矩在永磁体外圆弧半径3mm处时达到最小值(如图4所示)。电机反电势幅值随永磁体外圆弧增大而增大(如图5所示)。综合考虑齿槽转矩及反电势因素,选取永磁体外圆弧半径3mm为优化结果。
2.2 Halbach结构多极环的建模与仿真
本文设计的电机是内转子结构,多极环正弦充磁为外向聚磁型。理想的外向聚磁型多极磁环在Ansoft Maxwell中的极坐标下充磁方向设置为:R方向为cos(p*phi),phi方向为-sin(p*phi)。Phi为Ansoft软件自定义参数,相当于文中的θ。
式(4)和式(7)是在忽略定子开槽影响的情况下推导出来的电机气隙磁密计算公式。为了验证推导公式的正确性,建立Halbach结构多极环无槽定子仿真模型(如图6所示)。
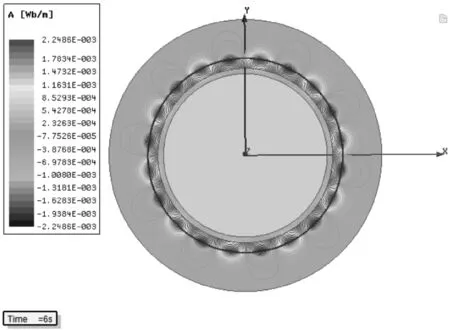
图6 Halbach结构多极环无槽定子仿真模型
电机模型的参数如表1所示。

表1 电机模型参数
根据表1数据,得到解析计算和仿真的气隙磁密(如图7所示)。解析计算和仿真的气隙磁密曲线非常接近,都为正弦波。仿真的气隙磁密幅值为1.24T,解析计算的气隙磁密幅值为1.26T,误差在1.6%,验证了解析法的正确性。

图7 Halbach结构多极环仿真和计算得到的气隙磁密
2.3 表贴式和Halbach的仿真分析比较
转子磁轭的厚度对表贴式结构电机非常重要,磁轭过薄,容易磁饱和,使气隙磁密减小,降低转矩;磁轭过厚,重量增加,降低转矩密度。采用Halbach结构多极环,其磁力线绝大部分从磁环内部穿过,磁轭厚度对电机转矩影响较小。转子磁轭厚度对Halbach多极环和表贴式结构的出力会产生影响(如图8所示)。
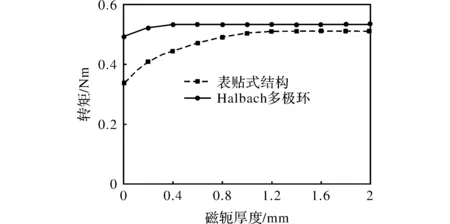
图8 磁轭厚度对Halbach结构和表贴式结构出力影响
磁轭厚度对表贴式结构影响较大,表贴式结构磁轭过薄,会严重降低电机出力(如图8所示)。采用Halbach多极环结构,转子磁轭厚度对电机出力影响不大,因此转子磁轭可以做得更薄,甚至可采用无磁轭,减小重量,在轻量化方面比表贴式有更广的应用前景。
本文的目的是开发一款高转矩密度轻量化无框力矩电机,因此在磁钢选择汝铁硼耐高温180℃的UH最高牌号。目前表贴式能做到的稳定生产的最高UH牌号为50UH,采用Halbach结构的烧结环,目前稳定生产的最高牌号为40UH。得到Halbach结构(40UH)、表贴式结构(50UH)和表贴式(40UH)三种转子结构在无槽定子仿真模型中的气隙磁密(如图9所示)。图9表明采用Halbach结构即便磁钢牌号只有40UH,所产生的气隙磁密比表贴式50UH的气隙磁密还要大。

图9 三种转子结构气隙磁密曲线
对表贴式结构(50UH)和Halbach结构(40UH)电机施加电流源激励,得到两种结构电机T-I(转矩随电流变化)曲线(如图10所示)。

图10 两种转子结构仿真T-I曲线图
由图10可知,采用Halbach结构转子在同样电流下,出力比表贴式结构大,在过载条件下,效果更明显。采用Halbach结构转子在高过载要求的使用领域有更大的优势。
3 样机与实验
为了比较表贴式转子(50UH)、Halbach多极环转子(40UH)两种结构的电机性能,本文设计并制造了一台无刷电机样机。为了防止由定子及机壳、转轴、端盖等零部件加工误差对试验造成影响,实验的电机除了转子之外,其余零部件都用同一套。
图11为两种不同转子结构的电机图片。图12为两种转子结构的实测的表磁波形。采用Halbach结构多极环的表磁,所产生的表磁比表贴式的表磁要大,表磁波形呈正弦形状。图13为两种不同结构转子实测的齿槽转矩波形。采用Halbach多极环的齿槽转矩周期不对称,幅值偏差大,这是由于目前采用Halbach结构的整体充磁技术不成熟造成的。整个磁环下,各个磁极分布不均匀,造成齿槽转矩周期不对称。图14为两种结构转子的转矩-电流曲线。采用Halbach多极环在额定点(0.5Nm)下,转矩常数比表贴式大7.6%。在过载(1.4Nm)下,Halbach多极环转矩常数比表贴式大21.6%。由此可见,采用Halbach多极环在提高电机转矩密度方面有明显优势,在过载情况下,优势更大。

图11 两种结构转子电机实物图
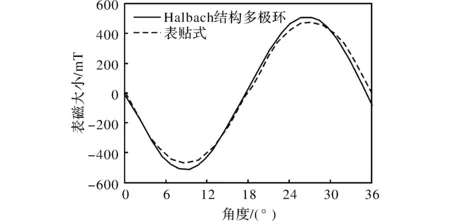
图12 两种结构转子表磁波形

图13 两种结构转子齿槽结构波形

图14 两种结构转子电机实测T-I曲线
采用Halbach结构磁环电机性能参数如表2所示:电机比德国TQ Robodribe的ILM 50×14转矩密度高12.7%。

表2 电机性能参数
4 结 论
为了研究Halbach结构多极环对无框永磁同步电机性能的影响,本文首先建立了该种转子结构电机的无槽定子解析模型,并用有限元方法验证了解析法的正确性。同时,为了证明该结构电机具有优越的电磁性能,本文分别建立了采用Halbach结构和传统表贴式结构的电机二维有限元模型,并从转子磁轭厚度、气隙磁密、T-I曲线三方面比较两种结构转子性能。最后结合样机实验数据得到的结论如下:①磁轭厚度对表贴式磁极结构影响较大,但对Halbach结构多极环影响不大,因而在电机转矩保持不变的情况下,后者可以做得更为轻薄,因而更适用于轻量化设计; ②转子采用Halbach结构多极环比转子采用表贴式结构产生更大的力矩,在高过载情况下,采用Halbach结构多极环优势更加明显。

