增大截面法加固空心板梁桥有限元分析
唐 杨,钟华栋
(1.重庆交通大学 土木工程学院,重庆400074;2.中铁二院成都勘察设计院有限责任公司,四川 成都 610081)
20世纪的桥梁建设由于设计理论不完善、施工水平低、工期紧迫以及后期的桥梁养护不到位等原因导致现在很多桥梁出现挠度过大、裂缝较多、混凝土破损以及钢筋锈蚀等病害。这些病害使桥梁的承载能力面临极大考验,同时很多桥梁由于在建时对交通发展的速度估计出现偏差,导致现在很多桥梁需要进行提载加固以适应现在的交通形势。桥梁加固的方法主要有:体外预应力加固法、粘贴钢板法、粘贴碳纤维布法、增大截面法、改变结构受力体系加固法等[1],其中增大截面加固法在近年来的中小桥梁加固方面得到了较为广泛的应用,通过相关文献可以看出拱桥的加固主要针对双曲拱桥[2-4]、石拱桥[5-6]以及小型的钢筋混凝土拱桥[7],梁桥的加固主要针对T梁桥[8-10]和空心板梁桥[11],其中空心板梁桥的加固较多采用粘贴钢板法[12]和粘贴碳纤维法[13],而采用增大截面法加固的较少。
本文以一座空心板简支梁桥为例,基于弥散裂缝模型理论,采用增大截面法对其进行加固,对比加固前和加固后桥梁的受力性能从而检验其加固效果,同时对影响加固效果的一些因素进行分析。
1 工程概况
位于宝成铁路上的某立交通道设计为空心板简支梁桥,桥长为12 m,计算跨径为11.6 m。空心板底面宽为5 m,顶面宽为5.5 m,护栏宽为0.5 m,梁高为0.9 m,空心板内共计7个圆孔,圆孔直径为50 cm,空心板的底板厚为20 cm,顶板厚为20 cm,边腹板厚为27 cm,中腹板厚为16 cm。空心板梁桥的平面布置和横截面如图1所示。

图1 空心板简支梁桥结构尺寸(单位:cm)
2 建立分析模型
分析模型采用Midas FEA有限元软件建立,共建立两个模型,一个为加固前的模型,一个为加固后的模型。为了能够模拟桥梁加固中空心板梁桥的二次受力行为[14],在有限元分析中采用施工阶段模拟[15]。加固后的模型考虑四个施工阶段:第一施工阶段中激活空心板梁桥的实体网格,并且激活支座边界条件和自重荷载;第二施工阶段激活混凝土湿重荷载;第三施工阶段激活加固部分混凝土的实体网格,钝化混凝土湿重荷载;第四施工阶段激活汽车荷载。加固前的模型只考虑两个施工阶段:第一施工阶段与加固后模型的第一施工阶段相同,第二施工阶段与加固后模型的第四施工阶段相同。
空心板梁桥采用C40混凝土,容重为25 kN/m3,弹性模量为32 500 MPa,泊松比为0.2,抗拉强度标准值为2.40 MPa,抗压强度标准值为26.8 MPa。考虑到计算过程的收敛难度以及空心板梁桥具体裂缝出现位置的不确定性,选用总应变模型中的弥散转动裂缝模型作为混凝土的非线性本构模型[16]。混凝土的非线性本构关系如图2所示,其受拉函数定义为常数函数,受压函数定义为Thorenfeldt函数,图2中ft为混凝土抗拉强度标准值,fc为混凝土抗压强度标准值。普通钢筋的容重为78.5 kN/m3,弹性模量为200 GPa,泊松比为0.3。为了考虑普通钢筋的材料非线性,采用范梅赛斯模型模拟钢筋的弹塑性本构,受力钢筋为HRB400钢筋,架立钢筋为HRB335钢筋,钢筋的非线性本构关系如图3所示[17],其中fy为钢筋的屈服强度。

图2 混凝土的非线性本构关系
模型中空心板梁采用实体单元建模,首先采用四边形单元划分空心板的截面网格,将截面网格纵桥向延伸得到3D实体网格。在顺桥向除了支座范围内均增加截面厚度,加固的部分混凝土同样采用实体单元建模,将梁底单元面向下扩展为3D实体网格,初拟加固厚度为10 cm。普通钢筋采用程序自带的钢筋单元模拟,不考虑钢筋与混凝土之间的滑移。为了避免支座位置的应力集中,采用软件中的印刻功能在梁底精确模拟支座范围,同时在支座范围的中心建立单节点单元,在单节点单元上施加一般约束模拟支座约束,单节点与支座范围内的梁底节点刚性连接。建立有限元模型如图4所示。

图3 普通钢筋的非线性本构关系 图4 有限元模型
荷载主要考虑有自重、混凝土湿重和汽车荷载。自重荷载因子Z=-1,混凝土湿重施加在空心板的梁底,以均布面力的形式施加。汽车荷载考虑为公路-Ⅱ级,根据简支梁的跨中弯矩影响线,将公路二级等效为车辆荷载加载于空心板梁桥上,荷载车前轴轴重75 kN,后轴轴重150 kN,车辆荷载布置如图5所示,荷载效率达到88.11%。
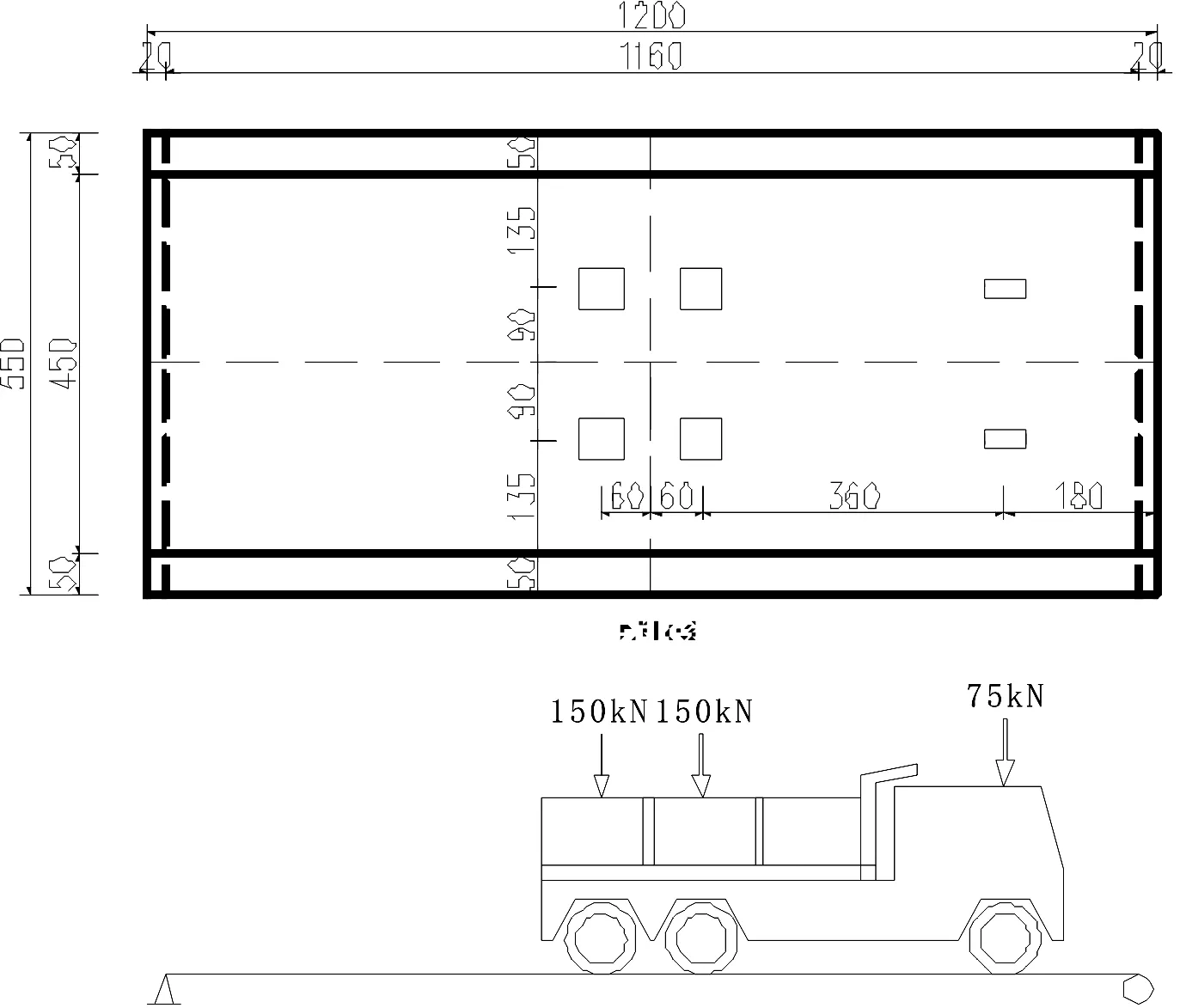
图5 汽车布载
在施工阶段分析控制中对非线性分析方法及加载过程进行控制,非线性分析的计算方法设置为Newton Raphson迭代法,除了在施加汽车荷载的施工阶段将加载步骤设置为5,其余施工阶段的加载步骤均设置为1,所有施工阶段的最大加载步骤数全部设置为30。
3 增大截面法加固效果分析
通过计算加固前和加固后在汽车荷载作用下空心板梁桥的受力,得到二次荷载作用下的挠度如图6所示,裂缝纵桥向分布如图7所示,裂缝竖向分布如图8所示。
由图6可以看出:加固前与加固后的最大挠度均出现在跨中位置附近,加固前空心板梁桥的最大挠度为4.42 mm,加固后空心板梁桥的最大挠度为3.85 mm,挠度最大值下降0.57 mm,下降幅度为12.90%。由图7和图8可以看出:增大截面法加固后,裂缝出现的位置仍然在原来的空心板梁,加固部分混凝土未出现裂缝。对比图7和图8:从加固前后的裂缝分布区域看,加固后空心板梁桥的裂缝区域减小;从裂缝延伸高度看,加固前空心板梁桥的裂缝已经向腹板发展,而加固后空心板梁桥的裂缝尚未发展到腹板;从裂缝宽度看,加固前空心板梁桥的裂缝最大宽度为9.71×10-3mm,加固后空心板梁桥的裂缝最大宽度为4.15×10-3mm,裂缝最大值下降5.56×10-3mm,下降幅度为57.26%。
通过增大截面法加固前后空心板梁桥的受力性能对比可以看出,增大截面法可以在一定程度上降低结构挠度,增强抗弯刚度,对裂缝具有较为显著的控制作用。总的来看,增大截面法的加固效果较为明显。
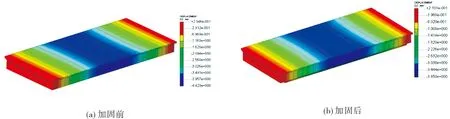
图6 加固前后空心板梁桥的挠度

图7 加固前后空心板梁桥的裂缝纵向分布

图8 加固前后空心板梁桥的裂缝竖向分布
4 加固效果的影响分析
4.1 加固混凝土厚度的影响分析
原加固模型中混凝土的厚度初拟为10 cm,现将加固混凝土的厚度分别设置为20 cm、30 cm,通过计算,提取不同加固混凝土厚度下空心板梁桥的最大挠度和最大裂缝宽度如图9所示,加固30 cm时空心板梁的裂缝分布如图10所示。

图9 不同加固厚度下空心板梁桥的受力性能

图10 加固30 cm空心板梁的裂缝分布
由图9(a)可以看出:随着加固混凝土厚度的增加,空心板梁桥的挠度先下降后升高,加固混凝土厚度由10 cm变化到20 cm,挠度下降0.10 mm,下降幅度为2.60%;加固混凝土厚度由20 cm变化到30 cm,挠度上升0.03 mm,上升幅度不到0.01%。由图9(b)可以看出:随着加固混凝土厚度的增加,空心板梁桥的裂缝宽度呈下降趋势,加固混凝土厚度由10 cm变化到20 cm,裂缝宽度下降1.18×10-3mm,下降幅度为28.43%;加固混凝土厚度由20 cm变化到30 cm,裂缝宽度下降0.20×10-3mm,下降幅度为6.73%。对比图9和图10可以看出:加固混凝土厚度由10 cm变化到30 cm,空心板梁桥的裂缝分布区域显著减小。由此可见,加固部分混凝土厚度的增加对空心板梁桥的挠度影响不大,但对空心板梁桥的裂缝宽度有较为显著的影响。
4.2 带筋混凝土加固影响分析
以上加固模型中的加固混凝土内不设钢筋,下面以10 cm、20 cm、30 cm厚度的加固模型为基础,在加固混凝土部分的底部设置一排直径为28 mm的普通钢筋作为受力筋,间距100 mm,由此对比带筋增大截面法与不带筋增大截面法在加固效果上的区别。通过计算,得到带筋增大截面法不同增大截面厚度下空心板梁桥的最大挠度和最大裂缝宽度如图11所示。
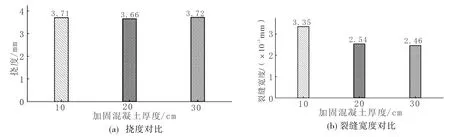
图11 带筋增大截面加固
由图11可以看出:在加固部分的混凝土中加入钢筋后,随着混凝土厚度的增加,空心板梁桥的挠度变化不是很明显,裂缝宽度有较为显著的变化,这与加固部分不加入钢筋时的变化规律相似。将图9和图11的数据对比分析,在加固部分的混凝土中加入钢筋后,10 cm、20 cm、30 cm加固厚度下的空心板梁桥的挠度下降幅度分别为3.64%、2.40%、1.67%;10 cm、20 cm、30 cm加固厚度下的空心板梁桥的裂缝宽度下降幅度分别为19.28%、14.48%、11.19%。由此可见,在加固部分混凝土中加入钢筋对空心板梁桥的挠度影响不大,但配筋可以有效降低空心板梁桥的裂缝宽度。
5 结论
依托宝成铁路某立交通道上的空心板简支梁桥,采用Midas FEA建立增大截面法加固前后的非线性有限元模型,对比分析了增大截面法加固前后空心板梁桥的受力性能,同时分析了加固混凝土厚度和是否配筋对增大截面法加固效果的影响,得到以下结论:
(1) 增大截面法可以在一定程度上降低结构挠度,显著降低裂缝宽度和减小裂缝分布范围,总的来看,增大截面法的加固效果较为明显。
(2) 加固混凝土厚度的增加对空心板梁桥的挠度影响不大,对空心板梁桥的裂缝宽度有较为显著的影响。
(3) 通过对比带筋增大截面法与不带筋增大截面法的加固效果发现,加固混凝土中是否配筋对空心板梁桥的挠度影响不大,但配筋可以有效降低空心板梁桥的裂缝宽度。

