既有劣化混凝土梁桥预防性养护策略研究

李斐然,丁 剑,赫中营

(1.河南省交通规划设计研究院股份有限公司，河南 郑州 450052;2.河南大学 土木建筑学院，河南 开封 475004)

目前,我国桥梁数量已居世界第一,其中99%以上为混凝土桥梁。随着桥梁服役时间增长,不同时期桥梁出现了不同程度的病害[1]。桥梁的养护任务愈来愈重,目前各省市均已成立或拟成立专门的桥梁养护部门,桥梁养护资金投入和技术力量都有长足的进步[2]。

当前我国颁布了《城市桥梁养护技术标准》(CJJ99-2017)[3]，不少学者对桥梁预防性研究提出了较为完善的集监测、评估、养护、修复、信息存储整理为一体的养护管理模式：高朝晖[4]结合传统桥梁养护管理系统中缺乏科学性、预防性、计划性的问题提出了B/S架构和WEB-GIS技术桥梁养护管理系统,解决了桥梁档案管理的混乱性与保持桥梁养护计划性长期性的问题;项贻强[5]基于桥梁的技术状况用全寿命分析(LCC)的思想,给出了利率影响作用下养护费用计算公式；宋伟伟[6]结合桥梁在Cl-影响下钢筋锈蚀模型预测了桥梁养护的最佳时机,但由于没有考虑养护费用的影响，说服力较弱；王巍、张春霞[7-8]构建了桥梁预防性养护效果、养护成本、耐久性寿命延长这3大目标，综合集成控制的优化模型并引入灰色模糊综合评判,为桥梁预防性养护时机和成本的选择提供参考和借鉴；王玉倩、陈艾荣[9]从不同部门角度出发研究了负责人在处理桥梁问题时所要达到的目标和处理时所用的层次分析方法，并从国家立场和企业立场两个角度研究了决策人处理桥梁工程决策问题时的目标和层次结构,并基于此建立了一种新的桥梁养护成本分类方法；曹明兰[10]详细阐述了要进行预防性养护的桥梁如何进行经济优化分析，并建立了桥梁自建成之日起到使用年限的养护经济优化分析的理论框架；吴斌[11]、杨航[12]、张霞[13]分别对混凝土桥梁预防性养护的重要性、混凝土桥梁常见病害类型及成因进行了分析和探讨,并提出了相应的混凝土养护策略;孙晶[14]根据现场实测数据，分析了桥梁在采用预防性养护与不采用预防性养护时桥梁运行期间的技术状况变化与养护成本；高峰[15]介绍了新时期公路桥梁养护现状、概念、预防措施,说明了公路桥梁的预防性养护是一种能够让管理成本大大减少,从而提高经济效益的重要工具。

综上所述,目前桥梁预防性养护的研究比较单一,只是对桥梁的养护方法和养护时机等进行研究,没有考虑桥梁的当前技术状况等级与养护费用之间的关系,也缺乏对桥梁预防性养护更深层次的研究。本文以河南省高速公路网郑漯段、安新段和宛坪段的混凝土桥梁为研究对象,以其当前技术状况等级为基础,结合养护费用和养护效果两个层面,分别对不同技术状况下的桥梁进行了预防性养护分析。

1 既有桥梁劣化情况统计

根据郑漯段、安新段、宛坪段既有混凝土桥梁的技术状况检测报告,3段线路中桥梁技术状况等级统计如图1所示。

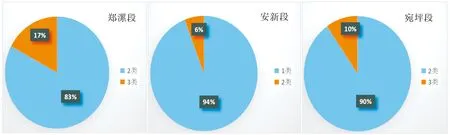
图1 桥梁技术状况统计结果

从图1可看出：郑漯段、宛坪段混凝土桥梁技术状况等级以2类、3类为主,且3类桥数量不足20%；安新段中混凝土桥梁技术状况等级较好,以1类、2类为主,且2类桥数量不足10%。依据实际检测报告,这3段线路中,2类桥及3类桥的劣化病害类型分别如表1、表2所示。

由表1、表2可知：既有混凝土桥梁中,最常见的病害是混凝土裂缝和钢筋锈蚀,这与既有研究成果相符。混凝土碳化及裂缝会引起钢筋锈蚀,后者会进一步产生或促进裂缝的扩展,这不但严重影响混凝土桥梁结构的耐久性,还会降低其使用效率,甚至降低混凝土桥梁的承载能力。为有效避免裂缝的发生和扩展,减小裂缝对混凝土桥梁的影响,在合理时期进行桥梁的预防性养护显得尤为重要。

2 既有混凝土桥梁劣化模型

桥梁使用过程中不同时期出现的劣化特征有所不同,主要包括：混凝土碳化、钢筋锈蚀、锈胀开裂和承载力下降,出现的顺序一般为：混凝土碳化-钢筋锈蚀-锈胀开裂-承载力降低[16],如图2所示。

由图2可知：在桥梁劣化模型中,锈蚀发生在混凝土碳化之后,钢筋锈蚀速度逐渐加快,直至构件锈胀开裂并达到极限承载力。钢筋锈蚀后结构劣化至极限承载力持续时间较短,因此预防性养护措施应在钢筋开始锈蚀之前实施。

根据我国桥梁建设历程及技术状况数据可知,目前我国高速公路2类和3类混凝土桥梁占比较大,该类桥在桥梁的劣化模型中属于混凝土碳化阶段,即在钢筋开始锈蚀之前,正是进行预防性养护的较好时机。

根据《既有混凝土结构耐久性评定标准》[17]，混凝土碳化残量x0及钢筋开始锈蚀时间tr计算公式分别为：

(1)

(2)

根据计算碳化残量x0和钢筋开始锈蚀的时间tr得出合适的时间区间进行预防性养护,进而提高桥梁的使用寿命。

3 养护效果及费用分析模型

3.1 预防性养护效果与持续时间

桥梁不进行预防性养护时，当桥梁的技术状况达到临界值时，桥梁的劣化速度会呈直线下降；桥梁进行预防性养护时，在相同时间下桥梁的劣化速度会显著降低。进行预防性养护时，劣化度γ的降低如图3所示，由于桥梁进行预防性养护时初始技术状况不同，所以会有不同的养护效果γi,劣化率变为θ(θ<α),养护效果消失后按原来的劣化率α劣化。

图2 桥梁劣化模型随时间的变化 图3 两种劣化曲线比较图

由以前桥梁的养护实例可知,桥梁进行预防性养护时桥梁的技术状况d越好，养护的效果越好，养护后作用的时间tpi越长。桥梁进行养护时养护效果与当前桥梁技术状况关系为：tpi=tpi(d)。桥梁首次进行预防性养护时，桥梁病害程度较小，故此时对桥梁进行预防性养护不仅可以很大程度提高桥梁的使用寿命，而且可以大幅延后下次的预防性养护时间；当桥梁再次进行预防性养护时,由于混凝土的材料特性、病害程度加深等原因，桥梁预防性养护后的效果较之前的养护会有所下降，桥梁预防性养护的持续时间也会相应减少,以此类推,桥梁进行预防性养护时选择合适的时间不仅可以提高桥梁的养护效果，而且还能节省大量的人力、物力、财力。假设桥梁处于2类或3类时第一次养护效果持续时间tp1,之后养护效果持续时间依次降低5%。在实际工程中,桥梁进行预防性养护后，由于受自然条件、施工技术、材料特性等原因，预防性养护效果会受到很大影响,因此需对tpi(d)引入分项安全系数：

βi=βa×βb

(3)

(4)

式中：βi为第i次预防性养护效果的分项安全系数,应考虑两种因素的影响，其中βa为混凝土龄期的影响系数,βb为多种因素之间的相互作用。在多种因素共同作用时要以环境作用为主，其他作用为辅进行计算,系数取1.0,在进行安全系数计算时，如果遇到某种环境因素作用较强时(环境因素影响等级超过2级),取0.9。

(5)

式中：n为桥梁自建成之日起到使用年限之前需要预防性养护的次数,0.05为折减系数,当桥梁运营期间周围环境变化不大时,βi与β1值相同。

3.2 预防性养护费用分析模型

桥梁在进行养护时需要考虑养护方案、养护开始时间，但最重要的是考虑桥梁服役期间的成本问题，在进行某桥梁的养护方案分析时首先要对其成本进行计算分析,力争用最少的资金对桥梁进行预防性养护。桥梁进行预防性养护时的费用包括两大类:材料费和人工费[18],当桥梁进行预防性养护时,假设预防养护次数为n,则单次养护费用Ci(i=1,2,…n)为：

(6)

(7)

由式(6)、式(7)可以看出：预防性养护时的养护费用Ci与养护方案有很大关系。合理安排首次预防性养护时间，合理选择养护施工方案可以减少养护费用。

式(7)中ci和n均为t1和ppl的函数,因为桥梁的使用年限较长,所以桥梁每次进行养护时资金价值不同,实际预防性养护费用计算模型为：

(8)

式中：C(t1,tpi)为桥梁预防性养护的总费用;C1(t1,tpi)为单次预防养护的费用,由式(6)计算;n(t1,tpi)为预防性养护的次数;r为社会折现率(%)。

4 最优养护时机

4.1 最优养护时机判定权值

将桥梁使用寿命的延长年限和养护成本的函数关系[19]作为最优养护时机判定权值,如式(9)所示。

(9)

图4 SPSS线性回归流程图

4.2 基于C语言的PSO算法

对式(9)所示权值的最优养护时机求解可采用微粒群(PSO)算法,其目标函数及条件约束方程[20]为：

约束条件：h≥hm；t≥设计使用年限

其中，h为桥梁养护前实测的桥梁技术状况,hm为桥梁进行预防性后希望达到的桥梁技术状况。

PSO算法的具体实现过程为：需要在一个N维空间中找出一个粒子的最优位置，首先假定一个拥有m个粒子的N维空间,其中某个粒子b的位置表示为向量xb(xb1,xb2...xbn),其速度也是一个n维向量,记vb(vb1,vb2...vbn)；其次评价粒子,得出此粒子此刻在这个n维空间中的最优位置pb(pb1,pb2...pbn)以及n维空间中m个粒子搜索到的最优位置pg(pg1,pg2...pgn)；然后更新粒子,粒子更新位置公式为：

vbn(t+1)=vbn+c1r1(pbn-xbn(t))+r2(pgd-xgd(t))

(10)

xbn(t+1)=xbn(t)+vbn(t+1)

(11)

式中：b=1,2,...m；n=1,2,...N;C1和C2为加速度常数;r1和r2服从[0,1]上的均匀分布。xbn(t)表示第b个粒子所处的位置,pbn是第b个粒子在N维空间中目前的最优位置,pgn是整个粒子群搜索到的最优位置,Vmax为粒子在N维空间中的速度极限。最后判断粒子是否满足输出,不满足输出条件时需继续执行评价粒子及更新粒子的命令。PSO算法的基本工作流程[21]如图5所示。

图5 PSO算法基本流程图

5 工程算例

某高速公路桥梁修建周期为两年，桥梁自通车之日起距今约15 a。桥梁规定的行车速度为120 km/h，双向四车道。桥梁建设使用材料为钢筋混凝土，支座结构采用常见的橡胶类支座，墩台采用钢筋混凝土材料(形状为柱形)。该段桥梁处于一般大气环境中,包括2类与3类桥,所以可以对此桥进行施工养护。桥梁预防性养护的施工方法有多种，本文采用常见的桥梁养护方法(表面涂有机硅烷渗透剂)。通过该养护方法找出桥梁在服役期间预防性养护时桥梁的养护费用与养护次数之间的最佳组合。

5.1 混凝土劣化方程及相关参数的计算

在桥梁建成5 a时对该段桥梁进行检测,将实测值代入式(1)～(2)中，得到相关参数，见表3。

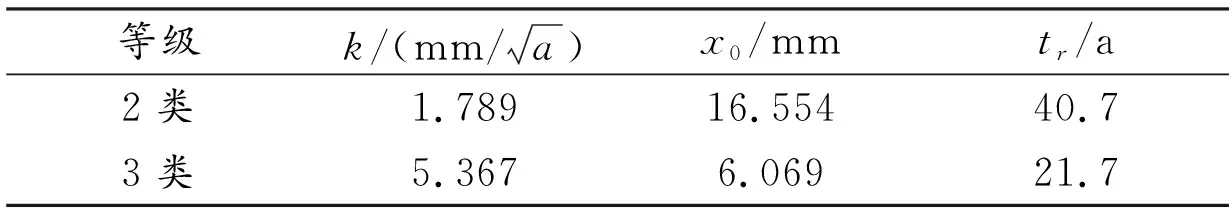
表3 碳化、锈蚀参数

由表3可知：当桥梁技术状况为2类时，距桥梁的设计使用年限(50 a)还有9.3 a;当桥梁技术状况为3类时，距桥梁的设计使用年限(50 a)还有28.3 a。因此，需要对桥梁进行预防性养护来提高桥梁的使用寿命。

图6 养护开始时间-延长年限关系曲线

5.2 预防性养护开始时间估算与寿命延长和养护成本计算

根据表2中的参数值,由式(3)和式(4)绘制出养护开始时间-延长年限关系曲线，如图6所示。

从图6可以看出：3类桥梁预防性养护延长年限较长,这是因为当桥梁的技术状况没有达到3类时进行预防性养护,可以很大程度提高桥梁的使用寿命；对于技术状况为2类的桥梁,虽经过检测桥梁技术状况较好,但由于养护开始时间较晚,桥梁材料的老化等原因会降低预防性养护延长年限。

5.3 桥梁的延长寿命年限、养护成本计算

由图6可以看出：桥梁预防性养护开始时间与持续时间关系曲线为抛物线,说明桥梁的预防性养护开始时间影响着养护成本,为进一步了解养护开始时间与养护成本的关系,根据式(5)～式(8)计算桥梁的延长寿命年限、养护成本,结果见表4、表5。

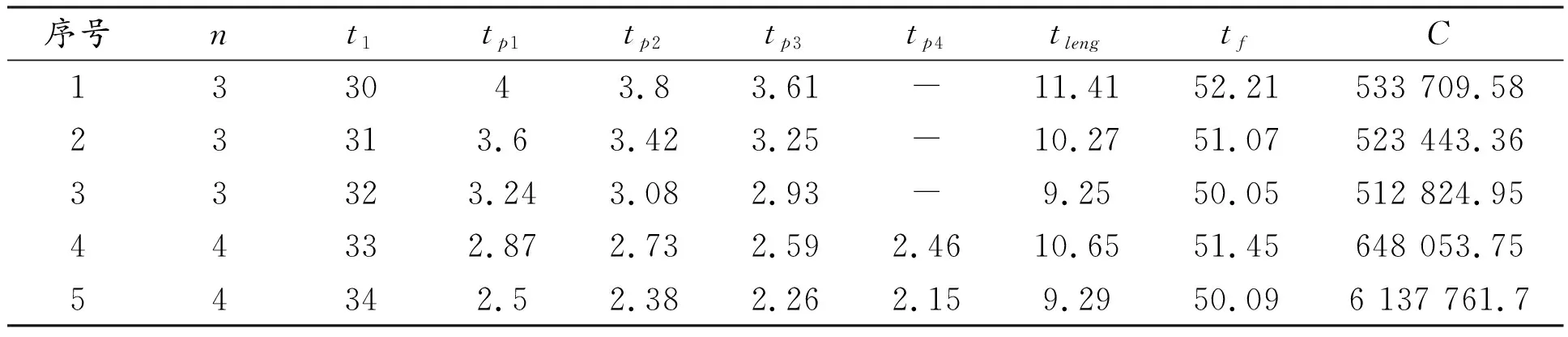
表4 延长寿命和养护成本计算表(2类)

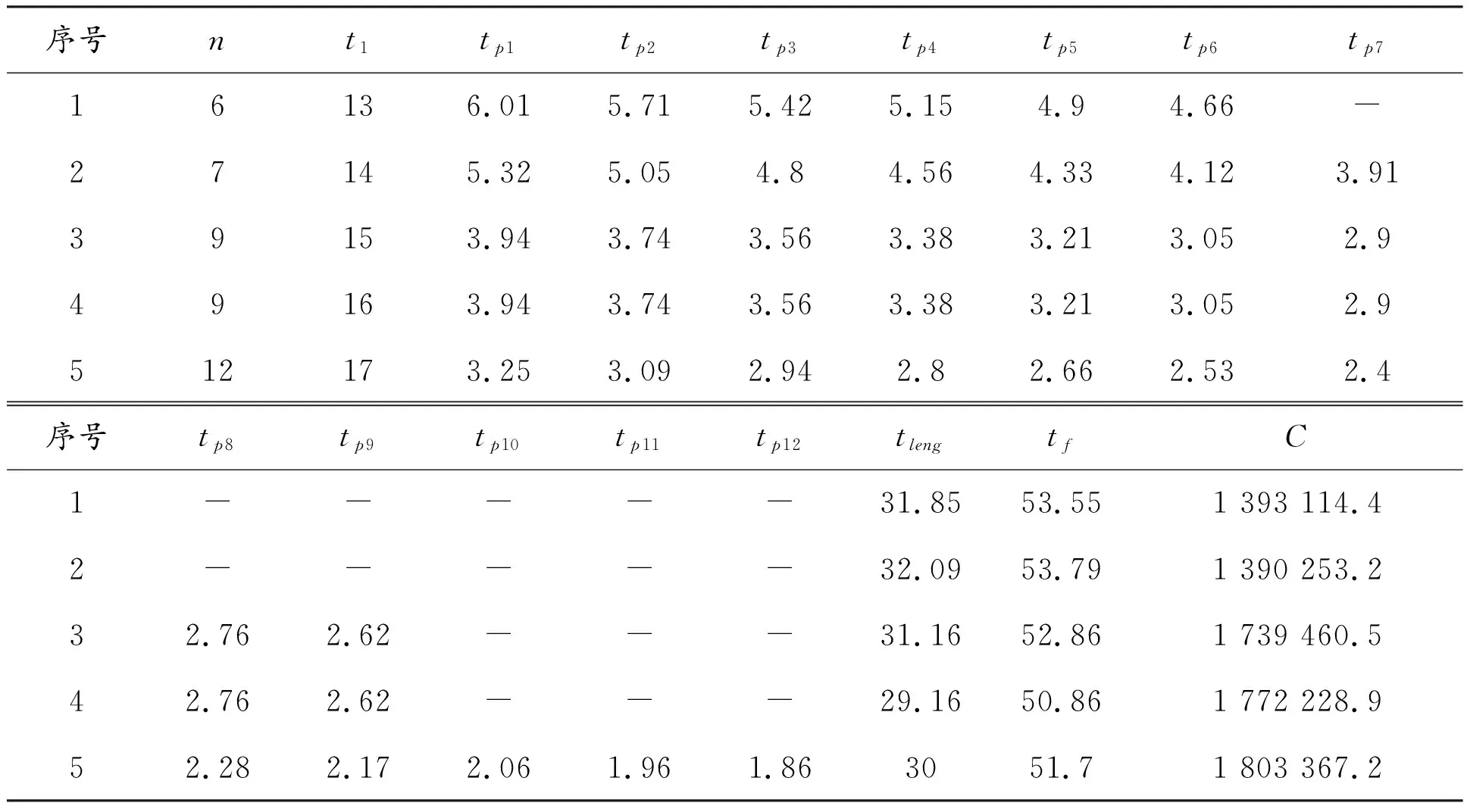
表5 延长寿命和养护成本计算表(3类)

由表4可知：桥梁进行预防性养护时,考虑桥梁服役期间预防性养护的费用最少,当桥梁技术状况为2类时，第一次预防性养护时间为第32 a,养护次数为3次,每次间隔时间分别为3.24 a、3.08 a、2.93 a，养护费用512 824.95元。由表5可知：桥梁技术状况为3类时，第一次预防性养护时间为第14 a,养护次数为7次,每次间隔时间分别5.32 a、5.05 a、4.80 a、4.56 a、4.33 a、4.12 a、3.91 a，养护费用为1 390 253.2元。

5.4 桥梁技术状况、总费用、判定权值的多元回归方程

假定判定权值在98%～100%时满足此桥梁养护的要求,根据式(6)、表4、表5中的数据,可得98%≤E≤100%，式(9)中各参数值如表6、表7所示。

表6 预防性养护回归方程中的相关参数(2类)

表7 预防性养护回归方程中的相关参数(3类)

E=-0.246 5C+0.013Ctleng-0.001C2+146.147

5.5 PSO优化

由4.2中的目标函数与约束条件可知：目标最优即意味着f趋近0,同时满足E、tleng较大、C较小。分别取E、tleng、C作为优先因子计算出目标函数f,选取目标函数f趋近0的值作为最佳优先等级,可计算出其优先等级为0.071 2、0.281、1,故在程序中目标最优的判定参数可选为：minf.f+1.0(-0.0712E-0.281tleng+C)。

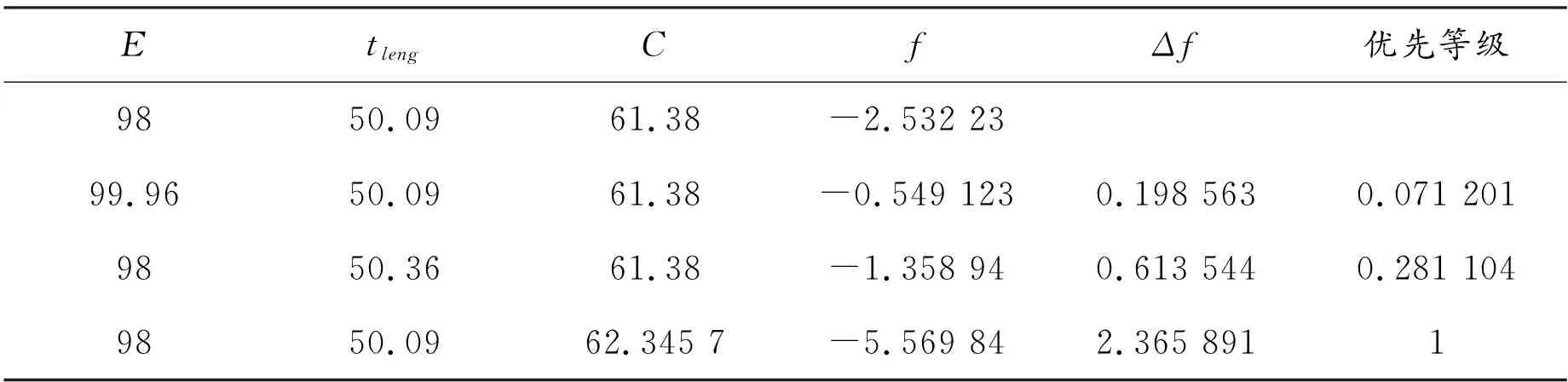
表8 E、tleng、C的优先因子

N维空间中微粒群体共有30个,加速度因子C1=C2=0.2,惯性权重取值为0.4～0.9,最大迭代次数取40 000,本文采用C语言编写该算例PSO算法程序。为了限制粒子在N维空间内,此案例中速度的范围设为-0.6～0.6。初始化后,用目标函数评价各粒子,得出当前的pid(i=1,2…30)与pgd,然后更新粒子,如此重复直到满足最大环次数或达到最优值的循环次数,运行结果如图7所示。

图7 微粒群优化算法编程运行后的结果

由微粒群优化算法计算结果可知：在满足桥梁的正常使用年限下用优化算法计算出来的结果更加精确,养护次数与养护费用更低,达到了较优的预防性养护目标。

桥梁技术状况不同时,桥梁的养护次数,养护费用会有所增加。为了更清晰地看出桥梁的养护次数与养护费用增加情况,根据表4、表5得出不同技术状况桥梁养护次数与养护费用的关系,如图8所示。

图8 不同技术状况桥梁养护次数与费用

从图8可以看出：当桥梁的技术状况由2类变为3类时桥梁的养护费用与养护次数增加较大。

6 结论

根据桥梁的劣化曲线及既有技术状况等级,考虑养护开始时间、养护效果持续时间、养护费用三种因素。采用了SPSS软件进行拟合,为保证得到更加精确的桥梁养护开始最佳时机，采用了微粒群算法对桥梁预防性养护时机进行研究,得出以下结论：

(1)桥梁首次预防性养护开始时间与桥梁首次检测时混凝土碳化深度有关,碳化深度越小，最佳首次预防性养护开始时间越晚。

(2)根据桥梁技术状况、养护成本、养护效果三个因素综合效益模拟出最优养护时机,并用SPSS拟合三者之间的关系和微粒群算法进行优化分析,可以达到最优养护目标。

(3)由算例可以看出，桥梁技术状况处于3类时再进行预防性养护,养护费用和养护次数增加较多，表明桥梁的最优养护策略与桥梁技术状况有关,缩短结构建成至桥梁病害发现时间可有效减少预防性养护次数和费用。