基于Walsh基和二值离散余弦基单像素成像的对比分析

李明飞， 袁梓豪， 赵琳琳， 孙晓洁

（1.中国航天科技集团有限公司量子工程研究中心，北京100094；2.北京航天控制仪器研究所，北京100039）

0 引言

压缩感知（压缩采样）（Compressive Sampling，CS）理论由 Candès等于 2006 年正式提出［1-2］， 美国Rice大学在2008年利用单像素成像实验验证了其有效性。CS理论是对稀疏或可压缩的信号进行少量非适应性的线性测量，可以近似100%地恢复出原始信号，可突破Shannon采样定理的限制，同时还具有超灵敏探测等优势［3］。目前，用于单像素成像压缩感知算法的测量次数仅为Nyquist采样极限的1%左右，即可重建出目标图像［4］。压缩感知算法是非线性迭代算法，且重建效果与所选稀疏基密切相关，故成像计算时间和稳定性同时受到极大挑战。而强度关联算法具有硬件要求低、成像速度快的特点，但其需要大于Nyquist采样极限的测量次数，故采样时间较长。

基于Walsh变换（Walsh Transform，WT）的方法提供了快速成像方案，该方案存在快速变换算法且硬件易于实现。采用二值矩阵作为调制矩阵，易于在高速数字微镜器件（Digital Micro-mirror Device，DMD）上实现。调制矩阵生成速度快且无需存储，Walsh矩阵作为测量矩阵具有正交特性，可完美重建图像。基于离散余弦变换（Discrete Cosine Transform，DCT）的方法也提供了实现快速单像素成像的方案，除了具有快速变换的特点和正交性的优点外，DCT基是连续的，更适用于图像压缩，这是也联合图像专家组（Joint Photographic Experts Group，JPEG）采用DCT作为图像压缩方案的原因。当然，DCT相比于WT的重要区别还在于DCT的连续性，在用于单像素成像时不利于实现快速光学调制，如DCT无法直接使用DMD实现20kHz的二值调制。文献［5］报道的抖动二值化方法使得DCT这类连续测量基实现高速调制测量成为现实，研究发现二值化后的DCT基与Walsh基非常相似，然而在单像素成像中二者谁更占优仍未有人研究。因此，在单像素成像中Walsh基和二值化后的DCT基各自优化排序后，哪一种成像信噪比更高和重建速度更快仍是值得研究的课题。

针对上述问题，本文开展了对基于Walsh基和二值化后的DCT基的单像素成像数值仿真实验对比研究。对DCT矩阵进行了抖动二值化，分别对比了在不同采样率条件下的基于两种变换的单像素成像信噪比和成像时间，对比研究了相同采样率下测量基三种不同排序时的单像素成像信噪比。

1 WT和DCT与测量基排序

1.1 WT与测量基

Walsh矩阵和Hadamard矩阵具有相同的矩阵元素，区别仅在于构造矩阵的行和列排列不同。Hadamard矩阵起源较早，应用极其广泛［6-7］。Hadamard矩阵（简称H矩阵）具有如下特征：1）矩阵产生速度快；2）矩阵元仅有1元素。矩阵任意两行（或列）正交， 有

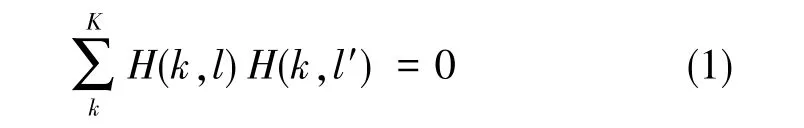
若K为矩阵阶数，则K需等于H矩阵的行数k或列数l，H（k，l）为Hadamard矩阵元。H矩阵正交归一，有HHT＝KI，I为单位矩阵，且满足H＝H-1。对H矩阵按逆序Gray码排序后可得到Walsh矩阵（简称W矩阵），设图像矩阵元为T（m，n），其二维WT的表达式如下

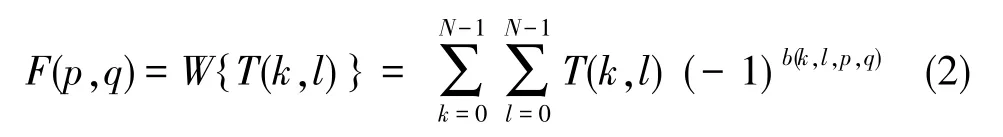
式（2）中，b（k，l，p，q）为对 2 取模运算， 其表达式为

式（3）中，g0（p）＝pn-1，g1（p）＝pn-1＋pn-2，g2（p）＝pn-2＋pn-3， …，gn-1（p）＝p1＋p0。 下标i＝0， 1，2， …，n-1分别对应ki、li、pi、qi二进制表示时相应的位。由于Walsh矩阵元为-1和1两种元素，需采用差分探测的方式，即先将矩阵元-1变为1，1变为0，构成D-1矩阵；将矩阵元-1变为0，1不变，产生D＋1矩阵，通过利用D＋1-D-1的方式来实现Walsh矩阵完整的测量。理论上全测量时，若图像大小为N×N，则全采样的测量次数为2×N×N，当采用互补调制［8］的方式时，实际测量次数需要N×N次。

1.2 DCT与测量基

二维DCT与离散Fourier变换（Discrete Fourier Transform，DFT）的数学表达式非常接近，实际上DCT就是DFT只截取余弦变换部分生成。二维DCT的数学表达式如下

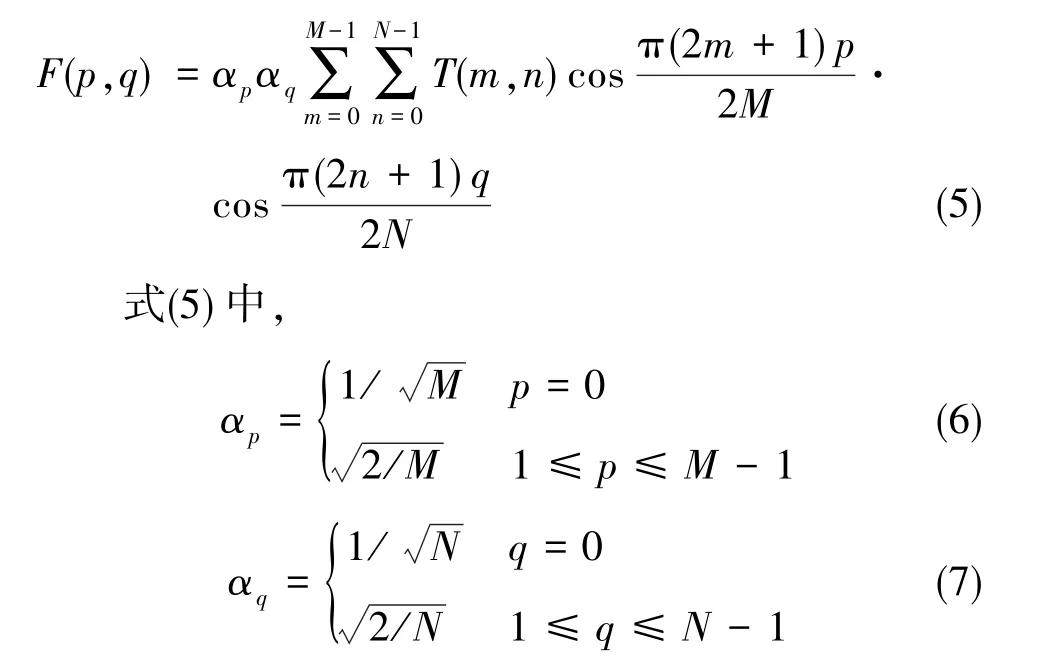
其中，M和N为物体的行数和列数，0≤m≤M-1， 0≤n≤N-1。

DCT矩阵和Walsh矩阵的测量基相似，但重要区别在于DCT是具有灰度的测量基。若采用DMD为调制器，按8bit灰度投影计算，DCT基测量速度是Walsh基测量速度的1／8，相应的单像素成像速度也将是Walsh基方案的1／8，全采样时二者信噪比相同。

经上述分析，从实际参考价值上看，编码同为灰度编码或同为二值编码的比较才能具有实际意义，直接使用DCT的灰度测量基与Walsh基比较则意义不大。

1.3 DCT基二值化-抖动算法

张子 邦 等［5，8］引 入 了 抖 动 算 法， 将 快 速Fourier变换（Fast Fourier Transform， FFT）有灰度的正弦图案转换成二值正弦图案，提高了基于FFT测量基的调制速度，使得单像素成像速度大幅提升。本文引入了抖动算法，将DCT基进行二值化，记为DCTb。不同于文献［5］和文献［8］之处在于，本文的DCT抖动二值化不对测量基进行上采样或插值，即抖动前后的矩阵均与原始矩阵大小相等，这样做的优势在于在实际应用中更加接近真实情况。

前文提到的抖动算法的核心思想是基于误差扩散原理，首先对当前像素值进行甄别，采用阈值法将当前像素值二值化后输出，然后将输入和输出的像素值之差按一定的权重传播到若干相邻未处理的区域。误差扩散原理可表达为

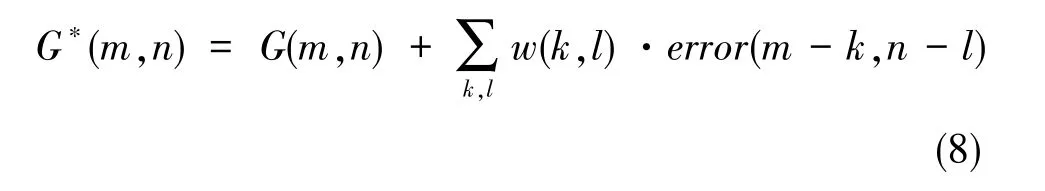
式（8）中，G（m，n）为输入的 DCT 图案，G*（m，n）为像素点（m，n）邻域像素加入的量化误差扩散值与输入图案灰度之和，量化误差error（m，n）扩散到邻域像素的二维权重函数（也称为核函数）为w（k，l）。T为阈值，归一化后的灰度图像一般取T＝0.5，像素值G*（m，n）可被二值化为抖动的图案b（m，n）， 其表达式为

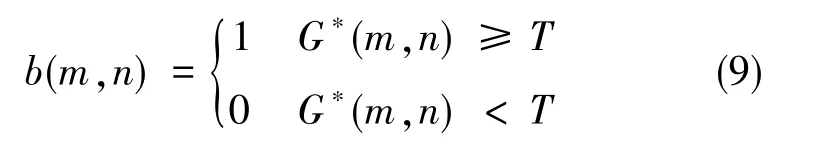
针对二值化DCTb矩阵，矩阵元的取值范围为［-1，1］，故要实现DCTb基调制，需要采用差分探测方案， 将式（9）中的 “0” 变为 “-1”， 与Walsh基相同。全测量时，若图像大小为N×N，则全采样的测量次数为2×N×N次。

1.4 测量基排序实现压缩采样

在文献［9］～文献［14］中均提出了Walsh基压缩测量的方案，并对压缩率与图像信噪比的关系进行了研究。上述研究的本质是对Walsh基的顺序进行重新排列从而选取测量系统较大的值来近似重建图像，在牺牲了一部分信噪比的前提下提升了重建速度。WT和DCT的压缩采样与传统的CS理论不同，WT和DCT的压缩采样是有损压缩，而CS理论可实现无损压缩。然而在实现效果和实用性上，WT和DCT测量基的压缩测量在图像探测、目标识别等方面具有优势，其计算时间复杂度为O［Mlog2（N）］， 算法效率高于 CS 理论的倍数接近其迭代次数，M为压缩测量次数。当图像越大，所需测量次数M越大，快速变换算法相对于CS理论的优势越明显。

1.5 不同测量基对比分析

WT和DCT的测量基均为正交基，可通过快速变换实现单像素成像，两者的区别在于：Walsh矩阵可通过1bit整数来表达，如在DMD的±12°两个方向实现光学测量；DCT测量基由连续的余弦函数演化而来，表达时需要用空间光调制器进行量化，一般采用8bit整数来表达，如用DMD多次调制来产生灰度阶的光强矩阵。在全采样条件下，WT和DCT的测量基均得到了理想的成像效果，且WT测量基的测量速度是DCT的8倍。然而在压缩采样时，DCT测量基因其灰度的连续性优势，压缩效率高于WT，故DCT成为JPEG图像压缩的标准。

然而，针对二值化后的DCT测量基，也可采用1bit调制矩阵元进行成像，此时究竟哪一组测量基表现更佳、更适用于单像素成像尚无明确结论。为得出具有指导意义的结论，本文参考文献［13］中的方法，对不同测量基的能量集中度、成像信噪比进行了对比分析。图像质量评价标准选择常用的两种方法，即峰值信噪比（Peak Signal to Noise Ratio，PSNR）和结构相似度（Structural Similarity， SSIM）。

2 实验效果对比

2.1 数值仿真方法

采用Lena图像作为测试对象。图1为Lena图像及相应的WT和DCT权重，即经相应变换后的系数绝对值，图像和权重矩阵均为128×128（像素）。

图1中，WT系数和DCT系数均进行了取绝对值操作，并归一化到［0，255］区间，用于显示和对比不同变换的权重。

在单像素成像数值仿真对比实验中，首先对Walsh基和二值化后的DCT基进行了权重排序，排序方法为：1）利用 STL-10数据库［15］选取其中80000张灰度图像，线性插值到128×128（像素）；2）对每一幅图像k分别作WT和DCT，得到变换系数图yk；3）对yk取绝对值，记为｜yk｜； 4）再分别对所有变换系数累加求和，即5）按累加结果对IB中每1个系数权值IB（i）由大到小进行排序，最终将获得通过图像训练得出的测量基顺序。训练得到的WT和DCT测量基顺序与原始 测量基顺序的对应关系如图2所示。

图1 不同测量基在图像变换后对应的权重Fig.1 Corresponding weights of Lena after WT and DCT

图2 训练排序与原序对比Fig.2 Comparison between the trained order and the original order

图2中，WT训练的测量基排序与DCT训练的测量基排序不同，反映出同一组图片在不同测量基下的权重系数不同，这一点在图1中也有体现。据此可以推测DCT和WT测量基对图像的信息获取效率将会有所差别，但哪种方式获取的效率更高还不能明确得出结论，需要进一步比较。

2.2 重建时间与能量集中度对比

图2中的排序在不同压缩采样下对应的采样系数谱图如图3所示。由于DCT和WT对图像特征的提取方式不同，故对应最优的采样排序策略也不相同。因此，本文考虑了更为公平的比较。通过80000张图像的训练后，相应的DCT和WT系数将各自训练出从大到小的序列，且各自相应的训练序列对于相应测量基均为最优排序。此时进行成像结果比较，显然更加客观。

图3 二值化DCT和WT在训练排序后的权重谱图Fig.3 Sampling weights spectral diagram of binary DCT and WT after the trained order

从计算效率和能量采集效率两个角度对比DCT和WT两种方法的优势，定义采样率符号为SR， 图 3（a）～图3（h）均为不同 SR 下得到的测量系数谱图。 其中， 图3（a）～图3（d）为用二值化的DCT测量基按DCT训练的不同排序采样SR（5%、15%、25%和50%）下对应的测量系数谱图，计算得出了相应的图像重建时间tDCT和能量集中度 ECR。图 3（e）～图 3（h）为 WT 测量基按 WT 训练的不同排序采样SR（5%、15%、25%和50%）下对应的测量系数谱图，同样计算得出了相应的图像重建时间tWT和能量集中度ECR。对比两组数据可知，在不同采样率下，无论DCT还是WT，重建时间基本保持不变，而ECR随采样率的增加而增大，符合理论预测；在相同采样率下，DCT重建时间在0.8ms数量级，小于WT的1.4ms；采样率为5%时，能量集中度DCT优于WT，随着采样率的增加，能量集中度WT优于DCT。

2.3 图像PSNR与SSIM对比

将图3中的权重谱图按对应的DCT和WT进行重建， 得到的结果如图4（a）～图4（h）所示。 其中，图4（a）～图4（d）为 DCT 测量基按 DCT 训练的不同排序采样SR（5%、15%、25%和50%）下对应的重建图像、图像结构相似度SSIM和峰值信噪比PSNR，图 4（e）～图4（h）为 WT 测量基按 WT 训练的不同排序采样SR（5%、15%、25%和50%）下对应的重建图像、图像结构相似度SSIM和峰值信噪比PSNR。

图4 二值化DCT和WT在训练排序后压缩测量单像素成像结果Fig.4 Compress and measure single-pixel imaging results of binary DCT and WT after the trained order

由图4可知，无论DCT还是WT，重建图像的PSNR均随采样率SR的增加而不断增大，图像视觉效果也变得越来越好；DCT重建图像的SSIM随采样率SR的增加也呈现上升趋势，但在SR＝50%时出现拐点，与视觉判断和PSNR趋势不符。WT重建图像的SSIM和PSNR均随采样率SR的增加而增大，图像质量变好。在低采样率条件下，SR为5%和15%时，DCT重建图像的PSNR和SSIM均优于同样采样率下的WT；然而在SR为25%和50%时，情况发生了变化，WT重建图像的PSNR和SSIM均优于同样采样率下的DCT，视觉效果与图像评价值判断结果相符。参考图3的能量集中度ECR，单从Lena图像的分析可知，在低采样率条件下，DCT方法占优；而在高采样率条件下，WT方法明显优于DCT。

2.4 重建图像评价值统计分析

扩大测试图像数据集，用统计的方法对重建图像的PSNR、SSIM和ECR进行量化对比分析，使得研究结论具有普适性。测试方法和重建过程与Lena图像研究方法完全相同，不同之处在于，测试图像样本数为随机从STL-10图库中抽取的500张图像，抽取图像与训练集中的80000幅图像无关。具体的实验步骤为：1）对500幅图像进行插值， 从 96×96（像素）变为 128×128（像素）； 2）利用DCT和WT分别对每1幅图像进行测量，测量基按训练权重排序，每增加1次测量，进行1次图像恢复，并进行ECR、PSNR和SSIM的计算，得到相应SR下的数值；3）重复对每1幅图像进行操作，并增加测量次数直到全采样，共进行16384次测量。按上述方法得到的数据如图5、图6所示。

图5 WT和DCT重建图像对应的SSIM和ECR与测量次数的关系Fig.5 Relationship between SSIM，ECR corresponding to WT and DCT reconstruction image and measurement times

图6 WT和DCT重建图像对应的PSNR与测量次数的关系Fig.6 Relationship between PSNR corresponding to WT and DCT reconstruction image and measurement times

图5表明，抖动二值化DCT重建图像的SSIM在测量次数为2458次左右、对应的采样率SR约为15%（2458／16384）时，其测量值优于同样条件下的WT。而WT的SSIM在采样率SR＞15%（测量次数＞2458次）时，其效果优于二值化的DCT成像结果。对于ECR，二值化的DCT在低采样率条件下也有相同趋势，即DCT的ECR优于WT；而在高采样率条件下，WT相比DCT更加具有优势。值得注意的是，二值化DCT方法的SSIM并不随测量次数的增加而增大，而是先增大后减小；而WT方法则随着测量次数的增加而增大。

进一步结合图像的PSNR对二值化DCT和WT重建图像进行分析，数据结果如图6所示。基于二值化DCT在压缩采样时重建图像的PSNR在采样率较低时（接近10%，对应的测量次数为1638），DCT测量值优于同样条件下的WT；随着采样率的增加，二值化DCT方法的PSNR先上升后下降，而WT方法的PSNR则随着采样率的增加而增大。通过与图5对比发现，PSNR、SSIM和ECR给出了一致的结果，即抖动二值化DCT在低采样率条件下的重建图像相比WT具有一定优势，PSNR在10%采样率（测量次数为1638）下均可达20dB；当采样率增大到50%（测量次数8192）左右，重建图像的SSIM可优于0.9，PSNR优于30dB，此时WT方法显著优于二值化DCT方法。

值得特别说明的是，二值化DCT方法重建图像的SSIM和PSNR曲线均随测量次数的增加先上升后下降，这说明随着测量次数的持续增加，重建图像的效果反而在下降，似乎与理论不符。分析其原因，由于对DCT测量基进行了抖动二值化，引入了量化误差，测量增加后编码空间网格变密，二值化的量化近似误差随之增大。因此，测量基的误差导致了重建误差，相关讨论可参考文献［16］～文献［18］。

综上所述，采样率小于10%时，二值化DCT方法重建结果优于WT方法；采样率在10%～20%时，WT方法的PSNR与二值化的DCT方法接近；在采样率大于20%时，WT方法的PSNR优于二值化DCT方法；相同采样率下，DCT图像重建时间略优于WT，但二者在同一数量级；在采样率低时，DCT方法的ECR优于WT方法，表明对于平滑图像，DCT方法更加有效。

3 结论

本文开展了基于WT和DCT测量基的单像素成像对比研究。针对抖动二值化DCT矩阵和WT方法，分别在不同采样率条件下对单像素成像的PSNR和SSIM、图像重建时间t和能量集中度ECR进行了研究。通过数值仿真对80000幅图像训练权重进行了排序，对压缩采样方案进行了优化，详细分析了Lena图像在抖动二值化DCT测量基和WT测量基的权重谱图和重建结果，并从STL-10图库中随机抽取500幅图像进行了量化分析。

在研究方法上，本文提出了图像训练权重排序方法，从新角度研究了测量基排序后压缩采样与单像素成像图像质量的关系。通过对DCT图像进行抖动二值化，使其可在DMD上快速实现，并在此基础上与WT方法进行了对比研究，研究方法具有指导意义。通过大量数值仿真，可以得到：采样率小于10%时，二值化DCT方法重建结果优于WT方法；采样率在10%～20%时，WT方法与二值化DCT方法效果接近；采样率大于20%时，WT方法重建图像质量优于二值化DCT方法。在相同采样率下，DCT方法的图像重建时间略优于WT方法，二者在同一数量级。该结论对实现快速、高PSNR单像素成像的测量基选取具有较好的参考价值。下一步，针对WT和DCT的压缩采样单像素成像仍有大量工作值得研究，包括针对不同图像先分类再进行优化排序、排序效果在实验系统的对比验证等，研究成果将进一步推进单像素成像技术的实用化。