核磁共振陀螺信号仿真及噪声分析

张 燚，汪之国，江奇渊，罗 晖，杨开勇

（国防科技大学前沿交叉学科学院，长沙410073）

0 引言

核磁共振陀螺（Nuclear Magnetic Resonance Gyroscope，NMRG）是当今新型原子陀螺中的一种。与微机电陀螺相比，NMRG具有精度高、耐冲击性强、加速度不敏感等优势［1-5］；与激光陀螺、光纤陀螺相比，NMRG具有体积小、易集成化等特点［1-5］；与其它类型原子陀螺相比，如无自旋交换弛豫（Spin Exchange Relaxation Free， SERF）原子自旋陀螺［6］、 原子干涉陀螺（Atom Interferometry Gyroscope， AIG）［7-8］， NMRG 又具有结构简单、 容易实现等优点。因此，核磁共振陀螺具有十分广泛的应用前景。其研究工作始于20世纪60年代末［9］，到 20世纪 80年代，美国的 Litton公司［10-11］、Singer-Kearfott公司［11-12］、 Stanford 大学［13］和英国的海军研究院［14］、 Sussex 大学［11］等多家单位已开展了相关研究工作，并制成了原理样机［15］。目前，在美国国防高级研究计划局（Defense Advanced Research Projects Agency，DARPA）支持下的核磁共振陀螺处于世界领先水平［16-17］。

典型核磁共振陀螺的基本原理是：利用碱金属原子磁力仪测量转动时惰性气体原子核磁矩Larmor进动频率的改变来得到系统转动信息［3］。与传统机械陀螺和激光陀螺相比，NMRG的结构复杂，包含多种光学、电学、热学器件，具有多种噪声来源，如激光器功率与波长的噪声、磁场噪声（包括磁场线圈电流不稳定引起的磁场噪声、由屏蔽桶效能有限引起的环境剩余磁场噪声、屏蔽桶本身及桶内其它器件的磁噪声）、温度漂移噪声、机械结构不稳定引起的噪声（如力学及热胀冷缩效应引起的光路不稳定）、信号处理量化噪声、电路噪声以及由测不准原理引起的量子噪声（如光子散粒噪声、光位移噪声、自旋投影噪声）等。且由于NMRG的体积限制，各种噪声彼此间存在较强的耦合，对陀螺信号的影响十分复杂。

但是，目前对NMRG中噪声特性的研究并不完善。由于决定NMRG敏感转动核磁矩的Bloch方程具有非线性特性，故难于解析求解。一般都是在Bloch公式的基础上采用稳态近似与旋波近似等手段获得理论公式的近似解，然后在近似结果的基础上分析系统的噪声特性［18-19］。这样虽能得到一些主要的噪声特性，但往往忽略了系统动态响应等重要性能，分析结果存在一定误差。另一方面，也有一些研究直接采用数值求解微分方程的方法来研究NMRG的系统特性［20］。该方法虽能克服近似解析方法对系统动态特性考虑不足的弊端，但是由于数值求解本身的收敛性问题，该方法一般只能获得较短时间内的系统特性。对于弛豫时间较长且需考虑长时间漂移的系统，处理起来就比较困难了。

因此，本文兼顾了解析与数值方法的优势：在理论模型基础上，对系统动力学方程进行时间离散化，在不采用稳态近似与旋波近似等手段的前提下推导出每一时间微元内的解析结果，并建立仿真模型，该模型不仅能够充分考虑NMRG系统动态响应特性，还能避免长时间数值求解的收敛性问题。并在此基础上，利用该模型分析了几种主要噪声来源对陀螺性能的影响，其结果对NMRG的研制与性能的提升具有重要参考意义。

1 理论模型

NMRG的基本原理如图1所示。

图1 NMRG的基本原理Fig.1 Principle of NMRG

首先，Xe原子核通过与Rb原子的自旋交换作用被极化后用来探测系统的转动角速度。Xe原子核磁矩K＝［KxKyKz］T满足如下动力学方程［18］

Ω由外界磁场B、Rb原子磁矩产生磁场bKSS及系统转动角速度ωr组成。 式（1）、 式（2）中，γXe为Xe原子核旋磁比；Γ1、Γ2分别为纵向与横向弛豫率，包含自旋破坏碰撞、原子与气室内壁碰撞、磁场梯度等弛豫效应；K0与自旋交换极化强度有关。

进一步令K＋＝Kx＋iKy＝K⊥e-iφ， 代入式（1）可得

式（3）中， Re［·］为括号中复数的实部。 在NMRG工作时，利用锁相环跟踪核磁矩绕z轴的转动相位，并在x方向施加与磁矩转动相差固定为β的激励磁场Ωx＝γXeB1cos（φ-β）， 且有Ωy＝0，可得

式（4）中，约等号使用了旋波近似，即忽略掉频率为2的项。

先考虑稳态解，令K⊥、Kz达到稳态，即⊥＝0、0，可得

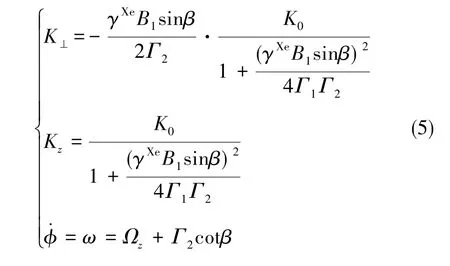
通过式（2）和式（5）可以看出， Xe核磁矩绕z轴转动的角速度ω与外磁场、Rb原子磁矩磁场、系统转动角速度、横向弛豫率以及锁相环输出相位差有关。

进一步考虑实时解，旋波近似下，式（4）分离变量后可得

式（6）所示的二阶常微分方程具有通解

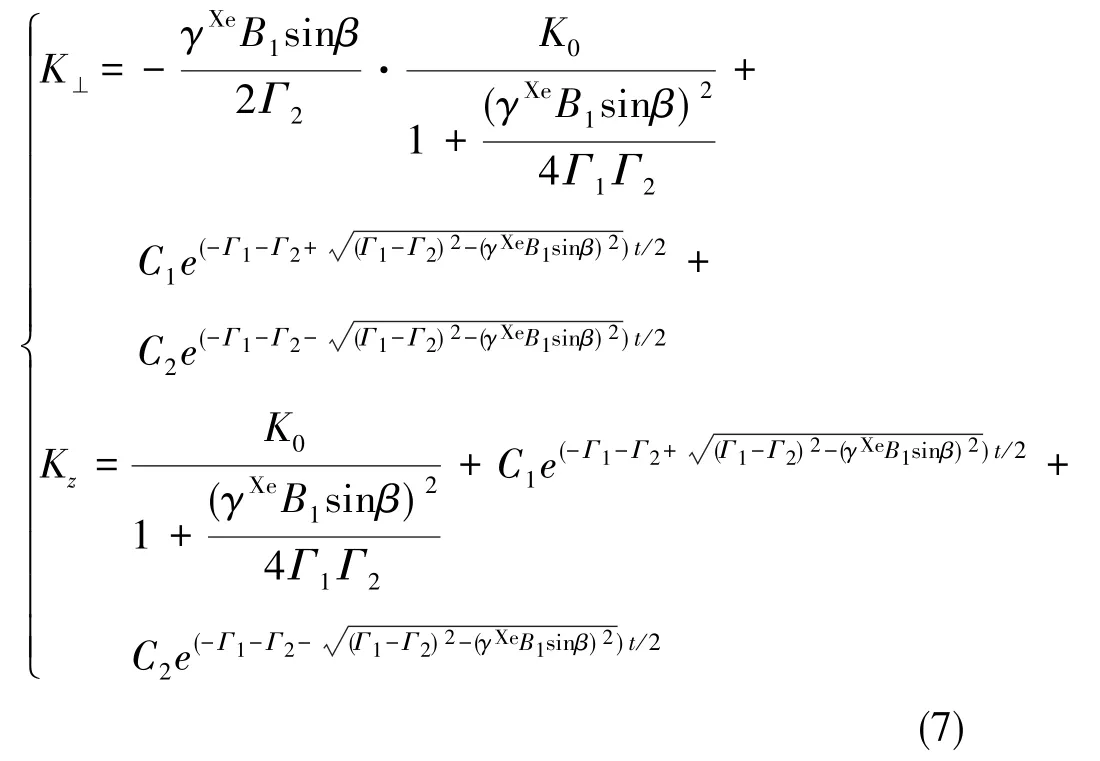
式（7）中，C1、C2由初值条件决定。 由式（7）可以看出，Xe原子磁矩的横向与纵向强度都以指数形式趋近于稳态，它们达到稳态的时间受横向和纵向的弛豫强度、锁相环输出相位以及横向激励磁场强度的影响，且弛豫越强，达到稳态越快。

由上述包含转动信息的Xe原子核磁矩产生的磁场信号可被NMRG中的内嵌Rb原子磁力仪探测，实现磁力仪功能的Rb原子电子自旋磁矩满足如下动力学方程

式（8）中，S＝［SxSySz］T为 Rb 原子自旋磁矩，S0为光泵浦与弛豫作用下Rb原子的稳态自旋磁矩，ΓA1和ΓA2分别为Rb原子的纵向与横向驰豫强度，γRb为Rb原子的旋磁比，Bx、By、Bz分别为系统感受到的x、y、z三个方向的磁场分量。在NMRG内嵌磁力仪中，Bz＝B0＋Bccosωct，Bx与By为探测到的Xe原子横向核磁矩产生的磁场。与Xe原子磁矩处理方法类似，令S＋＝Sx＋iSy， 可得

Jn为n阶第一类Bessel函数，化简后可得

实验时，通常只对Sx的特定模式进行测量，将正负频合并后有

进一步，由Faraday旋光效应，沿x方向线偏振探测光的偏振面转动角度θ与Rb原子沿x方向的磁矩Sx，n，p≥0成比例［18］

式（14）中，nAσ0为气室光学深度的倒数，L为气室特征长度，W为光跃迁线宽，Δ为共振偏移，P∞对应探测光的圆偏振二色性。实际测量时，是将通过气室后的线偏振探测光再通过一个偏振分光棱镜（PBS），利用通过棱镜后的光强来测量探测光偏振面的改变

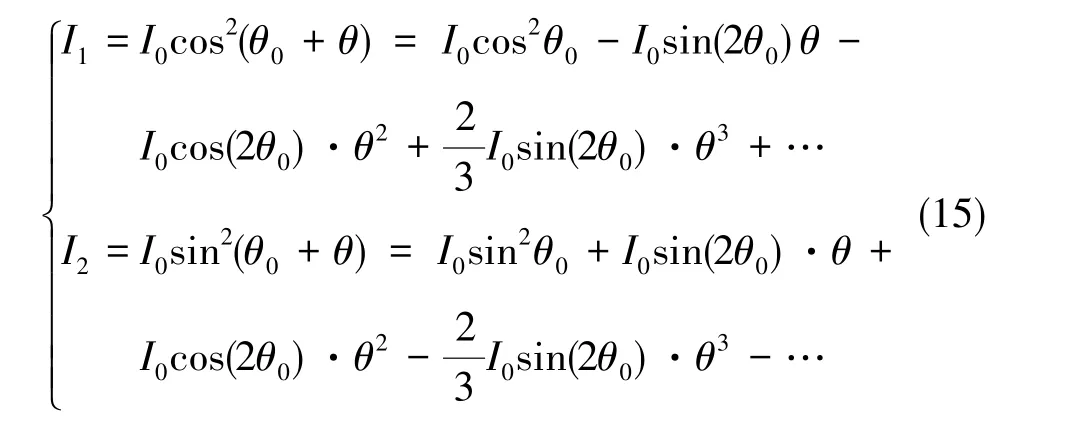
式（15）中，I1、I2为PBS后光电探测器探测到的两束光强，I0为通过气室后的探测光光强，θ0为探测光的初始偏振面夹角。测量时为抑制共模噪声，采用平衡探测的方法。调节探测光路，使θ0＝45°， 于是有

若进一步取共振条件ωc≈γRbB0， 式（16）与cosωct解调后，可得最终测得的光强信号

再代入式（5）的稳态结果后，可得NMRG的最终输出理论模型

由式（19）可知，陀螺最终输出信号与探测光强、气室大小、探测光频率、Rb与Xe的弛豫强度、极化强度、磁场大小频率以及锁相环相位等诸多因素有关，这些参数的任何非理想波动都会对陀螺信号造成影响。另外，需要注意的是，式（19）没有考虑实际锁相环的延迟，且对Xe原子磁矩采用了稳态近似。

2 仿真模型

根据上节理论分析，可以建立NMRG仿真模型，其程序流程如图2所示。

首先，为了进一步在仿真模型中考虑Xe原子核磁矩与锁相环的实时特性，需要对决定Xe原子核磁矩运动的Bloch方程进行时间离散化。考虑任意离散化后的时间微元，可以认为微元内除了核磁矩外其它物理量保持不变，于是有Bloch方程

求高阶导数分离变量后可得

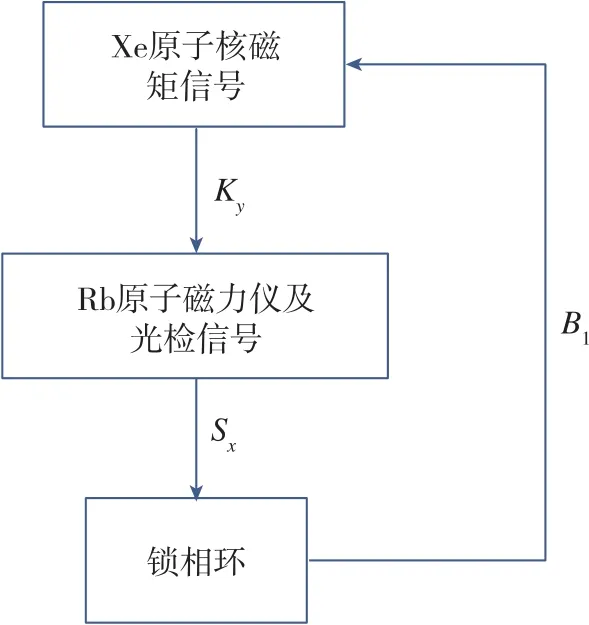
图2 NMRG仿真模型程序流程图Fig.2 Program flowchart of NMRG simulation model

常数 {c1，c2，…，c9}由初值条件决定。不失一般性，进一步假设时间微元内的初值条件K0＝［Kx0Ky0Kz0］T， 由式（20）可得

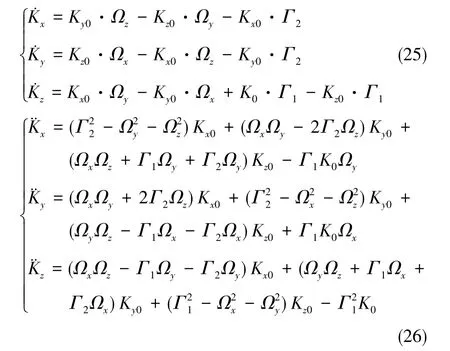
将式（23）的微分方程通解简记为K＝H＋c1ex1t＋c2ex2t＋c3ex3t， 其满足初值方程

代入初值K0＝［Kx0Ky0Kz0］T及式（25）、式（26）后，即可得到一个时间微元内Xe原子核磁矩的运动情况。

对于现实中一段时间内实时改变的物理量，可以先将其对时间微分，利用以上诸式考虑单个微元内的核磁矩运动，再将运动后的磁矩作为下一微元核磁矩运动的初值条件，进而得到任意时变物理量下的核磁矩运动情况。

然后，由式（17）可知，Xe核磁矩产生的磁场可被Rb磁力仪探测，并最终转换为光检信号输入到信号处理系统。这里，仿真模型处理Rb磁力仪信号没有采用时间离散化的方法，而是直接采用了式（17）的解析结果。这是因为Rb原子弛豫时间比Xe原子弛豫时间短得多，在Xe原子核磁共振特征时间范围内可以认为Rb原子磁矩能够实时达到平衡状态。

最后，类似式（19）的光检信号通过锁相环测得Xe核磁矩进动相位后，再通过横向激励场Ωx＝γXeB1cos（φ-β）反馈给Xe原子核磁矩的动力学系统。仿真时采用一个典型的二阶锁相环，其原理如图3所示。

图3 二阶锁相环原理Fig.3 Principle of second-order PLL

与前面理论分析不同的是：前面认为锁相环响应没有时延，能够及时得到核磁矩相位；而这里仿真用到的实际锁相环对相位的跟踪具有有限的跟踪速度。在仿真模型中，设置锁相环参数K1、K2， 如表1所示。由图4可知，此时锁相环能在1s内跟踪1Hz的频率突变，锁相环性能能够基本满足陀螺需求。为了更贴近实验，这里及后文的仿真都采用Labview程序进行。

表1 陀螺仿真参数Table 1 Simulation parameters of gyroscope

图4 锁相环对1Hz阶跃信号的响应Fig.4 PLL response to 1 Hz step signal

利用如图2所示的仿真模型，按表1设置仿真参数，对未出现的参数进行归一化处理，并令时间微元长度为1ms，即程序运行的采样率为1kHz，可得陀螺输出信号频谱分析结果，如图5所示。

由图5可知，陀螺输出信号频率在118.6Hz左右，信号幅度约为0.01V。同时，由于计算误差，陀螺信号中存在较小的噪声基底。根据陀螺信号，可以计算得到此时陀螺基于Allan方差的角随机游走、零偏不稳定性基本性能指标，具体如表2所示。

表2 各种来源噪声对陀螺性能的影响Table 2 Effects of noise from different sources

3 噪声分析

NMRG实际工作时主要受到磁场、激光、温度以及信号处理系统时钟频率的影响，故下面利用仿真模型分别考虑磁场B0、 探测光强、温度以及由时钟频率引起的锁相环相位噪声对陀螺信号及性能指标的影响。为了便于比较，且考虑到一般仪器精度，下面将各种来源的噪声都统一为初始设定值为1×10-5的均方根幅度、0Hz～500Hz带宽的均匀白噪声。

3.1 磁场B0噪声

对于磁场B0噪声，可能来自于产生磁场的线圈电流波动，也可能来自于外磁场波动。由表1可知，B0＝10μT。 因此，1×10-5的噪声幅度对应磁场为0.0001μT，其噪声谱如图6所示。

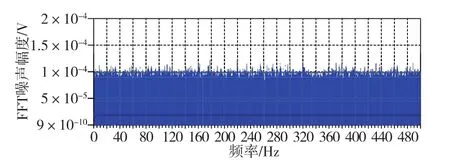
图6 磁场B0噪声谱Fig.6 FFT spectrum of B0noise

此噪声通过仿真模型后产生的信号噪声谱如图7所示。

图7 磁场B0噪声下的陀螺信号谱Fig.7 FFT spectrum of gyroscope signal with B0noise

由图7可知，磁场的均匀白噪声对陀螺信号118.6Hz附近影响更大，这可能来自于锁相环鉴相（PD）滤波器的影响。此外，陀螺噪声对低频的影响略大于高频，且对信号幅度本身没有显著影响。如此噪声对陀螺指标的影响如表2所示，可以看出，其对角随机游走、零偏不稳定性都有严重影响。

3.2 探测光强噪声

为了简便，这里只考虑了探测光强噪声的影响。由于探测光强已采用归一化参数，其具体噪声谱如图8所示。

此噪声通过仿真模型后产生的信号噪声谱如图9所示。

图8 探测光强噪声谱Fig.8 FFT spectrum of detection intensity

图9 探测光强噪声下的陀螺信号谱Fig.9 FFT spectrum of gyroscope signal with detection intensity noise

由图9可知，探测光强的均匀白噪声对陀螺信号各频段的影响相同，且对118.6Hz信号幅度本身没有显著影响。如此噪声对陀螺指标的影响如表2所示，其对角随机游走、零偏不稳定性的影响都比磁场B0噪声小了3个量级左右。

3.3 温度噪声

温度噪声主要通过Rb原子密度对陀螺信号造成影响，Rb原子密度的改变会影响Rb原子的极化率、极化磁场、弛豫时间以及Xe原子的极化率、弛豫时间等多种因素。这里温度的影响主要考虑式（2）中Rb原子极化磁场bKSS的影响，具体参数可参考文献［19］。其余极化率、弛豫时间等的影响，这里只取了简单的比例关系。一般Rb-Xe的NMRG运行时，温度需要保持在100℃左右，1×10-5的温度波动相当于1mK的温度波动，其噪声谱如图10所示。

图10 温度噪声谱Fig.10 FFT spectrum of temperature noise

此噪声通过仿真模型后产生的信号噪声谱如图11所示。

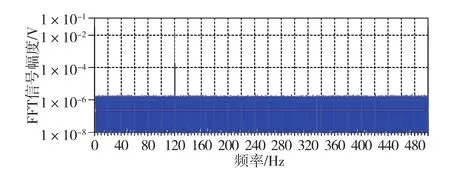
图11 温度噪声下的陀螺信号谱Fig.11 FFT spectrum of gyroscope signal with temperature noise

由图11可知，温度的均匀白噪声对陀螺信号各频段的影响相同，且对118.6Hz信号幅度本身没有显著影响。如此噪声对陀螺指标的影响如表2所示，其对角随机游走、零偏不稳定性的影响介于磁场B0噪声与探测光强噪声之间。

需要注意的是，真实系统中温度的扩散传播都需要一定的时间，而不是这里仿真模型中简单的参数改变，故真实系统对温度噪声的响应应该具有一定的低通特性。要更加准确的考虑温度的影响，需要通过有限元方法考虑温度的空间分布与传递，这已超出了本文所建立模型的范围。

3.4 锁相环相位噪声

真实陀螺信号处理系统的时钟频率也可能会有波动，这里将时钟频率的波动简化为式（25）中锁相环反馈相位β的波动。时钟每秒1×10-5的波动对于频率118.6Hz左右的信号可以等效为0.427°的相位波动，此时的相位噪声谱如图12所示。

图12 锁相环相位噪声谱Fig.12 FFT spectrum of PLL phase noise

此噪声通过仿真模型后产生的信号噪声谱如图13所示。

由图13可知，锁相环相位的均匀白噪声对陀螺信号118.6Hz附近影响更大，且以此频率为界，噪声对低频的影响略低于高频。此外，锁相环相位噪声也使陀螺信号幅度有明显下降。如此噪声对陀螺指标的影响如表2所示，与其它来源噪声相比，其对角随机游走、零偏不稳定性的影响最为严重。

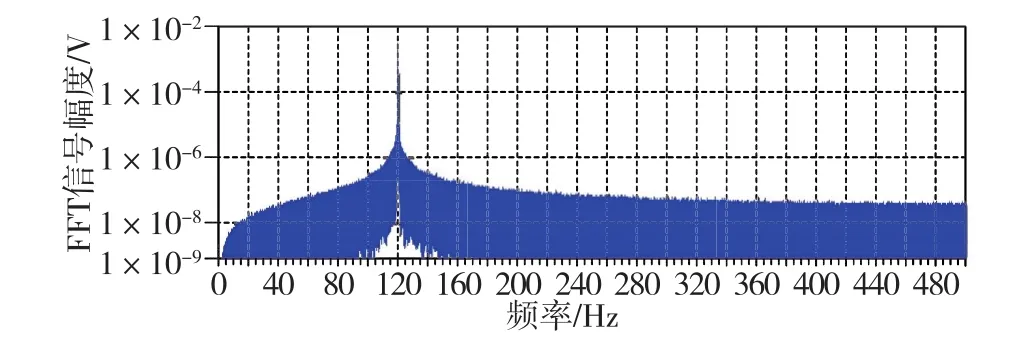
图13 锁相环相位噪声下的陀螺信号谱Fig.13 FFT spectrum of gyroscope signal with PLL phase noise

4 结论

本文首先在现有理论基础上，比较全面地考虑了NMRG中理想锁相环作用下的Xe原子敏感角速度的动力学方程、Rb原子磁力仪动力学方程以及基于Faraday旋光效应的平衡探测等内容，并构建出比较完备的陀螺信号理论模型。然后，在此理论模型基础上，结合时间离散化与解析求解等方法，在非旋波近似条件下建立起能够充分考虑NMRG动态特性的仿真模型。最后，利用该仿真模型重点研究分析了锁相环相位、磁场B0、温度以及探测光强在1×10-5幅度下均匀白噪声对陀螺信号的影响，发现它们对角随机游走、零偏不稳定性影响依次减小，且都具有自身独特的频率响应特性。在实际应用中，可以根据这些特性寻找主要噪声来源。

需要注意的是，本文的温度影响没有考虑实际温度传递扩散时间。可在进一步研究中将模型拓展为有限元模型，从而可以更加准确地研究温度以及其它物理场对陀螺信号的影响。此外，本文也未考虑双同位素的影响，但双同位素影响可在本文基础上简单拓展实现。实际上，双同位素可以有效抑制时钟频率波动或锁相环相位波动对陀螺信号的影响。