基于Bessel过程的波动率障碍期权定价

张继超，周 航，马 辉

(1.北华大学数学与统计学院，吉林 吉林 132013；2.长春大学经济学院，吉林 长春 130022；3.吉林农业科技学院，吉林 吉林 132101)

0 引 言

障碍期权[1](Barrier option)是一种最终收益为原生资产价格在整个期权有效期内是否达到某一规定水平(障碍)的欧式期权合约，它较普通欧式期权的价格便宜，因此在金融市场中受到更多投资者的关注.根据原生资产价格与规定水平的期权状态可以分为敲出期权和敲入期权.敲出期权是指原生资产价格在有效期内达到障碍，期权终止有效； 敲入期权是指原生资产价格在有效期内达到障碍，期权开始有效.目前在金融市场中关于原生资产价格设定障碍水平的衍生品类型较为完整，如障碍期权及其演化出的敲出障碍期权和敲入障碍期权、巴黎期权(Paris options)[2]等.一般在投资决策中准确预测原生资产价格的变化趋势更为重要，即对波动率的刻画.2007年[3]，法国兴业银行推出一种关于累积波动率的认购计时期权，该期权是一种预判股价或指数未来的波动趋势进而设定累积波动率阈值，当实际波动率累积达到预先设定阈值时才可执行的期权.与传统的欧式、美式期权等基础衍生品相比，这种期权提供了一种更为有效的控制标的资产风险暴露的方法.因此，计时期权产品不仅可以作为一种获取原生资产收益的重要方法，同时也是控制标的资产的波动率风险的有效工具之一.以上期权都为路径依赖期权，经典期权求解定价方法是以定价核或者转移概率为目标得到解析定价公式，但某些复杂期权只能得到数值解.期权定价理论的起源要追溯到1900年，Bachelier[4]首次运用随机游走描述股票价格变化，虽然不够成熟，甚至某些假设条件违背了市场实际情况，但他给出了波动率为常数情况下的欧式期权的解析定价公式.最近十几年，具有随机波动率的期权的研究已经成为金融衍生品定价研究的热点.为了更准确地描述金融市场，有效地对期权进行定价，许多学者开始关注随机波动率模型，例如Hull-White随机波动率模型[5]、Heston波动率模型[6]等.目前，随机波动率模型下期权定价的研究主要集中在欧式型期权定价问题，而对于路径依赖期权[7]定价的研究较少.因此，本文研究具有Hull-White波动率模型下的一种特殊的欧式障碍期权的定价问题.

1 相关知识

在期权定价中，经典的Black-Scholes公式[8]给出了标准欧式认购期权的价格如下:

V(S，t)=SN(d1)-Ke-r(T-t)N(d2)，

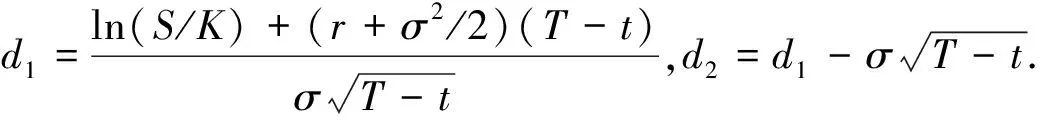
通过对资产价格时间序列的数据分析可知，资产价格波动率σ不是常数，而是一个随机变量. 1987年，Hull和White[5]首次提出了扩散波动率模型(Hull-White模型)，在风险中性概率测度P下，假设标的资产价格St和标的资产的方差vt满足如下随机微分方程：

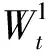
假设Rt服从指数为γ(≥0)的Bessel过程[10]，且R(0)>0，

(1)

其中B(t)是标准一维布朗运动.

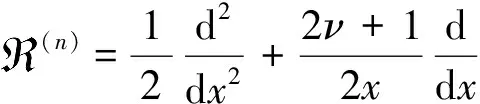
其中，Px是以x起始点确定的概率测度.

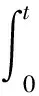
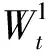
命题1构造投资组合Πt=U(t)-Δ1G(t)-Δ2S(t)，在风险中性定价理论下，则Hull-White模型下的波动率障碍期权价格U(t)满足下面的偏微分方程

本文简化考虑ψ=0情形.波动率障碍期权价格U(t)满足非抛物型偏微分方程，比普通障碍期权多出第3项vUI，它是关于累计实际波动率的导数.

2 定价公式

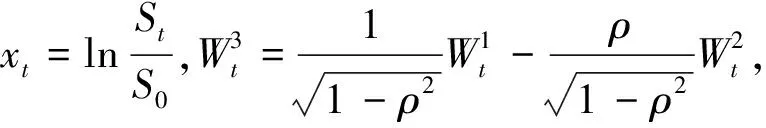
(2)

(3)

由式(2)得

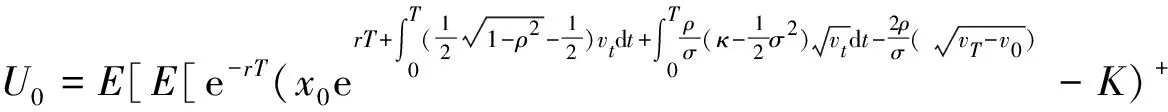
(4)

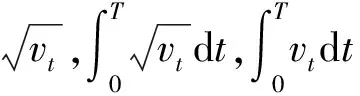
(5)

其中

(6)

(7)

(8)

由此，我们得到：

定理1假设标的资产对数价格xt和随机波动率vt满足Hull-White随机波动率模型变换过程式(2)和式(3)，在到期时刻的期权收益为U(T)=(ST-K)+ΙτB>T，则波动率障碍期权价格U0表示为式(4)，且条件期望中联合密度函数为式(5)～(8).

3 小 结

现实金融市场中波动率衍生品的价格或是基于离散样本股票的价格，或是由连续价格的二次变差得到实际方差后的价格，本文利用Bessel过程给出解析定价公式可有效应对连续时间条件下随机波动率模型的期权定价问题.特别地，Bessel过程的性质是我们得到关于累积波动率的特殊障碍期权闭型解析解的关键.本文提出的波动率障碍期权也丰富了金融交易产品.