Fuzzy矩阵复合运算的单调收敛性研究

关却东智，索南仁欠,2

(1.青海师范大学 数学与统计学院，青海 西宁 810008；2.青海师范大学 研究生院，青海 西宁 810008)

0 引言

本文在“基于Fuzzy矩阵复合运算新定义的性质研究”的基础上，研究了模糊矩阵复合运算的基本性质，并且引入幂序列的概念与几种特殊模糊矩阵，如对角占优矩阵、数量矩阵、对角矩阵等.同时研究并讨论模糊矩阵与特殊模糊矩阵在改造的Fuzzy复合运算，即(max-·)型复合运算下其单调性与收敛性.其中，单调性是研究模糊矩阵的幂序列是否收敛的基础.而模糊矩阵的收敛性对数值计算有着重要的作用，它对数值计算结果具有直接的影响.模糊矩阵的收敛性是研究模糊系统稳定性的前提[7].因此，讨论研究(max-·)型复合运算下的单调性与收敛性是有必要的.总之，通过对比发现：虽然Zadeh算子的复合运算的代数性质比(max-·)型复合运算要好许多，但(max-·)算子在有些方面具有优良的性质.

1 预备知识

定义1.1 单调矩阵：设A=(aij)m×n，B=(bij)m×n，C=(cij)m×n∈T(U)，U为论域.规定：

*：[0,1]×[0,1]→[0,1]

*为[0,1]上的二元算子.

1)序关系：A≤B当且仅当aij≤bij，i=1,2,…,m；j=1,2,…,n.

2)单调性：若A≤B，则A*C≤B*C.

3)单调矩阵：若A≤A2，Ak≤Ak+1，则A称为单增矩阵.若A≥A2，Ak≥Ak+1(k≥1)，则A称为单减矩阵.单增矩阵与单减矩阵统称为单调矩阵，其中记A*A=A2，Ak+1=Ak*A.

定义1.2设R∈F(U×U)

1)若任意的u∈U，都有R(u,u)=1(或0)，则为R在U上是自反的(或反自反的).

2)若任意的u，v∈U，都有R(u,v)=R(v,u)(若u≠v，且R(u,v)>0时有R(v,u)=0)，则为R在U上是对称的(或反对称的).

3)若任意的u,v∈U，都有R∘R(u,v)≤R(u,v)，则为R在U上是传递的.

4)若模糊矩阵R∈MF(U)，满足自反性、对称性时称R是U上的模糊相似矩阵.

5)若模糊矩阵R∈MF(U)，满足自反性、对称性、传递性时称R是U上的模糊等价矩阵.

定义1.3

1)单位矩阵：存在模糊矩阵E，使得E*A=A*E=A,其中

2)零矩阵：矩阵中所有元素都为0的矩阵，由O表示.

3)数量矩阵：所有非主对角线元素全等于零的矩阵，由D表示.

2 改造以Zadeh算子为模糊矩阵的复合运算

定义2.1当论域U有限时，模糊矩阵R和G的复合运算记为R∘G，并规定：

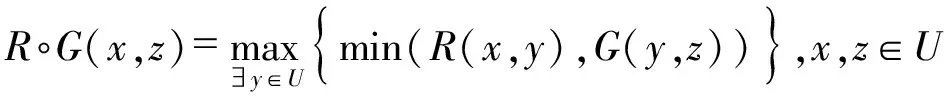
(注)这里给定的以Zadeh算子为模糊矩阵的复合运算是多种算子系列中的一种，即(max-min)复合运算，也是Zadeh算子作为运算符号的一种符合.比较其他算子而言，它更具一般性，具有最好的代数性质，运算量也简单.但应用Zadeh算子时主观意识对总体判断具有显著影响，而且许多隶属度在取小取大后所带信息在计算和应用中没有起到作用，相当于损失了某些信息，这是不利的.

一般而言，模糊矩阵的复合运算以什么方式或选择什么算子，取决于模糊集或者模糊关系时采用了某种模糊运算.因此，对给定的二元运算*，可以定义R∘G为模糊矩阵R和G的复合运算，其中举例说明比较特殊的两种复合运算：

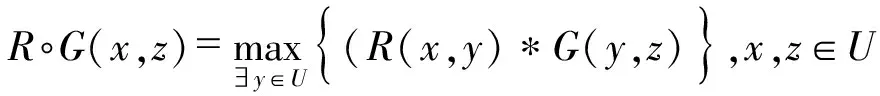
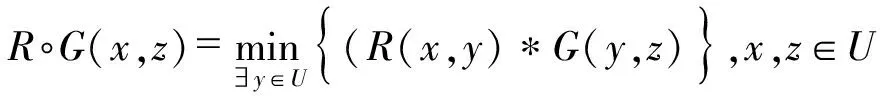
这样的改造可以视具体情况而定，但在实际中不同的研究对象，选用适当的算子来描述是比较困难的，因此研究这些算子的代数性质是人们所希望的.

由于实数的集合具有序关系，因此能够诱导出以下关系：

∧=min与∨=max

本文对∧与min，∨与max不加以区分.

通过研究分析表明，如果二元运算*满足结合律且在[0,1]2上处处非减，则(max-*)或(min-*)复合运算也是可以结合的，且对并运算满足分配律(结论1).故得到矩阵的幂定义，即

R1=R，Rk+1=Rk∘R∀k≥1.

矩阵的幂定义可以得到R的一个幂序列，本文重点研究幂序列的单调性与收敛性.

本文将二元运算*选取为普通意义上的乘积，即a*b=ab，a,b∈[0,1]，则复合运算为

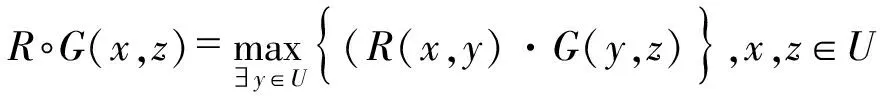
命名为(max-·)型复合运算.

根据上述分析我们可以得到一些简单的结论(结论2)，即

1)结合律：A∘(B∘C)=(A∘B)∘C.

2)并分配率：A∘(B∪C)=A∘B∪A∘C(A∪B)∘C=A∘C∪B∘C.

3)交分配率：A∘(B∩C)=A∘B∩A∘C(A∩B)∘C=A∘C∩B∘C.

(注)交分配律在Zadeh算子下不成立.

证明A∘(B∩C)=∨∃k[aik·(bkj∧ckj) ]

=∨∃k[aik·bkj∧aikckj) ]

=[∨∃k(aik·bkj)]∧[∨∃k(aik·ckj)]=A∘B∩A∘C

4)交换律：若A，B都是自反的，则A∘B=B∘A.

证明因aik·bkj≤min∃k{aik，bkj}且A，B都是自反的，使得

又因aij∨bij=bij∨aij，所以A∘B=B∘A.

5)单调性：若A≤B，则A∘C≤B∘C.

其余结论的证明是显然的，故在此略去.

下面我们将研究改造后的(max-·)型复合运算的单调性与收敛性.最基本的性质请参看文献[1].比如文献[1]中研究了自反性、对称性、传递性、等价关系、λ-截距阵等相关内容.

3 模糊矩阵复合的单调性

定理3.1若A∘B=C，则A∪B≥C.

证明因aij∨bij≥∨(aik·bkj)=cij当且仅当aik=bkj=1时等号成立.

推论3.2若A∘B=C，则max(A，B)≥C.

推论3.3若A∘A=A2，则A≥A2.

推论3.3说明在(max-·)算子下模糊矩阵永远都是单减矩阵，因此，我们只讨论单减矩阵.但事实上，对于这类矩阵具有更为常用的名字，称为传递矩阵.

图1中的MN1和MN2都工作在亚阈值区域，MP1、MP2和MP3具有相同的宽长比，所以Iout=Iref。由于电阻RS的存在，MN1和MN2的VGS不相等。设MN1的尺寸与MN2的尺寸的比值为K，电阻RS两端的电压为IoutRS，忽略体效应的影响，即VTHN1=VTHN2，由IrefRs=VGSN2-VGSN1可得[14]

定义3.1设A=(aij)n×n∈MF(U×U)，若任意i，j∈{1,2,…,n}，都存在aij≤max{aii，ajj},则称A为对角占优矩阵.

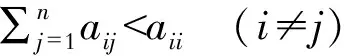
则称A为严格对角占优矩阵.

定义3.3任意给定λ∈F(F为数域)，Fuzzy阵A与λ的数乘记为λA，其中λA=(λaij)m×n.

定理3.4设A为n阶Fuzzy对角占优方阵，P为n阶置换矩阵，若(bij)=P'AP(P'为P的转置矩阵)，使得bii≥b(i+1)(i+1)，1≤i≤n-1.

定理3.5若A是对角占优Fuzzy方阵，且有aii·aij≥ait·atj，则

证明首先由定理3.4知，任意对角占优方阵都在某个置换矩阵下将主对角元素排序，且有bii≥b(i+1)(i+1)，1≤i≤n-1，故不妨设A的对角元素为a11≥…≥aqq≥app≥…≥ann，因为aii·aij≥ait·atj，

对任意给定的i，j都存在k，使得不等式

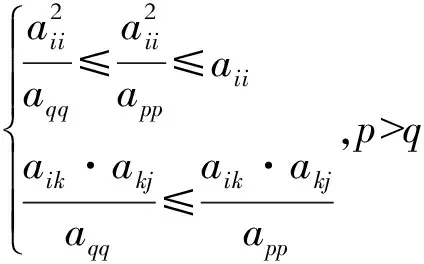
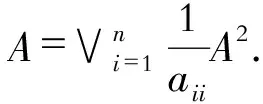
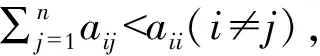
从而由定理3.5可知，推论3.6成立.

推论3.7若A是对角Fuzzy方阵，则

此类等式为模糊矩阵的幂序列单调恒等式.

4 特殊模糊矩阵复合的收敛性

定义4.1收敛性：设A为U上的模糊关系(矩阵)，若对任意的x,y∈U，数列{Ak(x,y) }k≥1都收敛，则称A是收敛的.

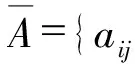
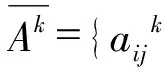
以下用此定义无限收敛.

aijk+P=aijk

(1)

满足式(1)的最小正整数K，P分别称为A的收敛指数与周期指数，且分别记为Ak，AP.当Ak不存在，而limk→∞aijk存在时，则称A无限收敛.因此，有以下结论：

定理4.1设A是n阶Fuzzy阵，aijk无限收敛当且仅当limk→∞aijk=0.

证明⟹：无限收敛定义可知，

⟸：显然.

定理4.2若A是n阶对角Fuzzy阵，则Ak无限收敛.

证明因A=diag(a11,a22,…,ann)，可得Ak=diag(a11k,a22k,…,annk)，所以定理4.1得，limk→∞aiik=0，可知Ak无限收敛.

推论4.3设A是n阶Fuzzy阵，若在置换矩阵P下能对角化，则Ak无限收敛.

证明因P＇AkP=P＇AP…P＇AP，由定理4.2知Ak无限收敛.

推论4.4 设A是n阶Fuzzy数量阵，则Ak无限收敛.

证明根据数量矩阵的定义知，A=mE，所以Ak=mkE，故收敛.

下面由一例子来直观描述上述结论.

在(max-·)型复合意义下，可得

k不管是偶数还是奇数，显然都有

因此，Ak无限收敛，说明A在(max-·)型复合运算下收敛.