核心素养背景下的深度备课

唐希明　蒋楠　曾宁宁

摘 要：立德树人及核心素养如何与“五项核心指标”相融合？怎么样落实在课堂上？学生的“学习力”是如何在课堂上发生的？教研应该怎样助力学生提高学习力？本文努力通过所思所想给出我们的想法和做法。

关键词：学习力 见识和认知 自我教育 核心素养 深度教研

中图分类号：G633.6文献标识码：A文章编号：1003-9082（2020）03-0-02

普通高中课程是实现高中阶段育人目标的重要载体。在落实立德树人根本任务中发挥着重要作用，而数学核心素养即是在充分挖掘数学课程对落实立德树人根本任务的独特育人价值，而将这一任务落实在实处却有相当的困难。因而在核心素养背景下探索数学教学中渗透思想教育就成为可能。通过课堂这一最为基本的形式，尝试将教师的教学行为与课堂紧密相联，促使数学核心素养在课堂中落地生根，从而响应立德树人的根本任务。

一、数学教研中关于教研的思考首先考虑的是育人价值

“立德树人”的基本内涵不仅仅包括帮助学生掌握必需的知识、技能、思想、方法、提升学生的数学素养，而且强调在学生形成人生观、价值观、世界观等方向发挥数学育人的功能，而六大数学核心素养的主线是从知识立意到能力立意，再上升到素养立意。我们认为，其中最为主要的变化是“思维品质”的变化，而这一点正是加强了学生素养的

培养。

“立德树人”中另外一个侧重点是人的培养。数学育人应当体现人性。我们发现“学习力”才是要引起我们高度关注的对象。“人脑是可塑的，是人的活动在塑造人脑的发展”（程介明语：香港大学副校长），人类的学习是通过经历给周围的事物赋予意义，从而形成概。所以，我们认为，无论从国家层面“立德树人”还是提升“核心素养”，其核心任务是如何让学生形成“学习力”，学生的核心业务就是学习力的产生。

二、数学教研中对“学习力”的关注和理解

五项核心指标，总结起来就是一句话，如何促使学生“学习力”产生。那么，“学习”是怎么发生的？背后的逻辑是什么？我们对“学习”该存怎样的认知。

人脑是可塑的，是人的活动在塑造人脑的发展，因此，人类学习是通过种种经历给周围的事物赋予意义，从而形成概念，学生的核心业务就是“学习”。在这个层面上，种种经历就是给学生在课堂中展示概念的产生、发展、形成的全过程，从而形成观察、归纳、类比、迁移的数学学习习惯，是一种自然而然的，理所当然的发生，这样才有一种亲近感，是符合人性的。

三、数学教研不能只靠经验，应该有“学习”做为支撑

在课堂上，学生为什么要这样学习，到底学得好不好，如何评判，这就是我们对学习力的最终理解。经验是用来借鉴的，不是用来复制的。“学习”的基本操作可分解为剖析、鉴定、检修、确定、质疑等。另一方面，人类的学习是一个群体运动，这是人类和其它动物的最大差别，所以群体学习，小组学习，协作学习，师生、生生互动也就成为了最有效的学习方式。

四、数学教研要考虑见识和认知

我们可以发现这样一个变化，见识促使认知结构方式的变化，才能产生“学习力”。所以在课堂设计中，加入一些认知下产生的变化，虽然是一点点变化，其结果都会大不相同。所谓见识，就是经理、体验、犯错、修正、见多识广、格物而至致。所谓认知，就是当你遇见陌生问题所持的思维方式，即解决问题之时，认知便开始了！而任何的教学中的不到位，都是由认知的不到位引起的。所以核心概念的深度理解，对一节，一章乃至高中整个体系的认知，就是设计课堂的源泉，而要想认知是合理的、全面的，见识则是基础，动手尝试，想象力都是见识的基本表现。

在以上对核心素养解读、参照“五项”核心指标的理解、指导课堂的设计的基础上，我们将述总体思想分拆成以下五个方向，对课程的设计进行全面引领。我们以《》复习课为例加以

说明：

1.知识要点透析

这是最为基础的目标，即能力目标的载体，首先是对核心概念的深度理解。

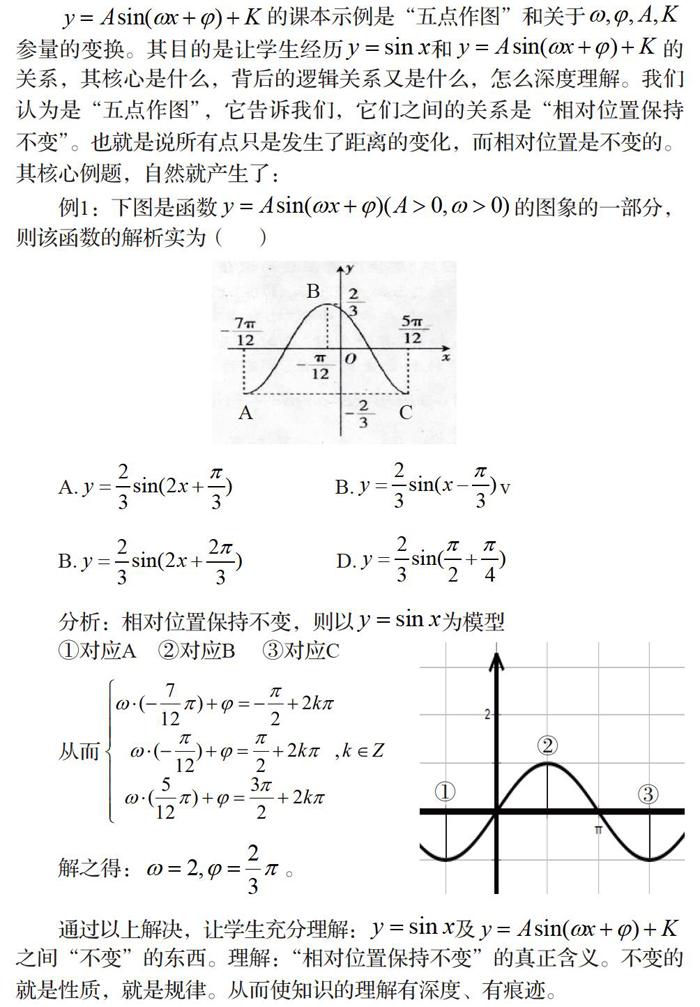
的课本示例是“五点作图”和关于参量的变换。其目的是让学生经历和的关系，其核心是什么，背后的逻辑关系又是什么，怎么深度理解。我們认为是“五点作图”，它告诉我们，它们之间的关系是“相对位置保持不变”。也就是说所有点只是发生了距离的变化，而相对位置是不变的。其核心例题，自然就产生了：

例1：下图是函数的图象的一部分，则该函数的解析实为（）

A.B.v

B. D.

分析：相对位置保持不变，则以为模型

①对应A ②对应B③对应C

从而

解之得：。

通过以上解决，让学生充分理解：及之间“不变”的东西。理解：“相对位置保持不变”的真正含义。不变的就是性质，就是规律。从而使知识的理解有深度、有痕迹。

2.能力要求透析

在以上对知识的深度理解之上，继续引领学生促使从知识到能力的变化。能力六大核心素养：数学抽象，数据分析，数学建模，逻辑推理，直观想象，数学运算。其核心要义是要求学生在知识理解的基础上产生创造性的应用。创造性的应用即为能力的体现。为此：产生如下例题为母题。

例2：设函数，若函数在区间上具有单调性，且则函数的最小正周期为（）

A B C D

分析：知识的迁移，即当我遇到陌生的问题时，认知便开始了，

。由“五点作图”可知：对称轴为，

由，知对称中心为。则

由于“相对位置保持不变”，且他们是相邻的，故而创造性的应用这一知识点的迁移，从而自然而然的产生了能力的发生。我们分析这一过程。

①观察产生联想，此点必须对相关知识点要有足够的深度理解。

②归纳产生数学抽象，进而知其对称轴和对称中心。

③从数据分析产生逻辑推理，进而用的单调性，及三个数值及先排序后。通过验证，知符合题设。

④以上产生能力：观察（提出）、发现、分析、解决、实际问题的能力。

从中我们发现：能力的产生是一个不断对知识进行内化的过程。所以经历、尝试、想象力必不可少。理解了这个认知的变化规律。在其基础上进行问题的设计、训练才是有效的。

3.素养要求透析

在能力产生之后，我们认为所谓数学素养，就是自然而然、水到渠成，也可以理解为形成一种数学思维习惯。这种科学的数学思维习惯根植于心，素养自然就形成了。其数学育人的目标之一，是做一个讲道理，守法则，讲诚信的人。为此，就形成了如下母题。

例3：某湿地公园围了一个半圆形荷花池塘，如图所示，为了提升荷花池的观赏性，现计划在池塘的中轴线OC上设计一个观景台D（点D与点O，C不重合），其中AD，BD，CD段建设架空木栈道，已知AB=2km，设建设的架空木栈道的总长为km。

（1）设，将表示成的函数关系式，并写出的取值范围;

（2）试确定观景台的位置，使三段木栈道的总长度最短.

分析：所有运动变化的，在数学里就是函数，所以第一步表达函数式就是自然而然的事情。

，其中定义域的求法则需求的是能力：即当D与C重合时，取到的最大处。此时。

第二步：问题的解决。转化求此函数的最小值。观察产生联想，从而产生第二种最为朴素的想法：第一种，使用導数

令得到又时，是的减函数。时，是的增函数。时，。此时=。故当D位于线段AB的中垂线线上且距离AB为km处时，满足条件。

第二种，，

对于，为A（0，2）和

的连线的斜率：而对于B（）是单位圆的一部分进而解决问题及解。

在这里，由能力到数学素养是自然形成的。让学生体会学习的过程。体会问题的提出到问题的解决所遇到所有困难是如何使用最基本的知识点解决的。从而人脑得到再塑，知识得到深刻理解。达到学以致用的效果。

4.人文关怀透析： 数学育人

可以看出，学生在再刚刚接触到题目时，是会感到压力的，要知道使用和理解是一个过程的两面，是同时发生，就像骑自行车，只有你骑上去，才知道什么是平衡。从已知会的这点出发，结合知识、能力通过不断尝试、分析、再尝试。展开想象力并坚持不放弃的执着。最终使得问题得到解决，心中愉悦感油然而生。很明显，这一内容对于数学抽象、数学运算、逻辑推理和数学建模能力的培养，再渗透思想教育，使得这一节的最终目的得以实现。在这一过程中应关注学生遇到的困难，给予学生一定的鼓励和支持。

5.自我教育透析：自我成长

任何教育，我们认为其实质都是自我教育。用自我厚重的数学功底去影响唤醒学生。从五个维度关注课堂设计，关注备课。教师自我才是最大的收益者。在备课中，并不是一味的追求结果。而是领会在追求结果的过程中所得到的收获。引导学生树立正确的价值观。

参考文献

[1]何建东.数学教学中的“智”“惠”数学通讯[J].2019（6）下（23-27）

[2]王尚志.数学教学研究与案例[M].高等教育出版社.

[3]教育部考试中心.普通高等学校招生全国统一考试大纲的说明[M].高等教育出版社.

[5]史宁中，王尚志.普通高中数学课程标准（2017）解读[M].高等教育出版社

[6]教育部.普通高中数学课程标准（2017）[M].人民教育出版社.

作者简介：唐希明，（1966.11.20），男，汉族，河南滑县人，中学数学高级教师，银川唐徕回民中学首席教师，宁夏大学首批特聘专家，国家奥林匹克数学高级教练员，自治区首届“9.10”教育奖章获得者，银川市首届“十佳”教师，银川市第一届，第二届名师工作室主持人，人教A版教材专家组成员，山西，重庆，广西，贵州特聘教研员，国家考试中心评价组成员。理学学士，主要研究方向，数学教育，数学教研及数学教材解读。

蒋楠（1985.12.07），男，汉族，宁夏灵武人，银川唐徕回民中学，中学一级教师，理学学士研究方向：数学教育，数学教研。

曾宁宁（1986.03.27），女，汉族，黑龙江伊春人，银川唐徕回民中学，中学一级教师，理学硕士，研究方向：数学教育，数学教研。