做一个严谨的思考者

周炼

在学习几何的过程中，当我们面对一个未知的、需要我们自己画图来解决的问题时，可能会遇到一些条件交代模糊，位置关系或数量关系不确定的情形。这时我们需要仔细审题，对“模糊元素”进行缜密分析，有时需要分类讨论，做一个严谨的思考者，养成思考问题严谨缜密、细致全面的思维习惯。下面给出两种同学们常见的易错类型，供同学们参考。

例1 已知线段AB=6cm，P是线段AB的中点，C是直线AB上一点，且AC=1/3AB，则CP=____。

【錯解】只考虑点C是线段AB上一点，根据作出的图1，AB=6cm，因为P是线段AB的中点，AC=1/3AB，得到AP=1/2AB=3cm，AC=1/3AB=2cm，从而得到CP=AP-AC=3-2=1cm。

【分析】由于本题没有给图，所以有的同学在自己画图的过程中考虑问题不全面导致错解，没有关注到条件“C是直线AB上一点”中“直线”这一个“位置模糊”的元素的表述，从而没有对点C可能的位置进行思考与探究，只画出了点C是线段AB上一点的情况。

在解决此类问题时，我们需要对题中关于描述位置的条件仔细斟酌、反复推敲，充分考虑“位置模糊”的元素所有可能的位置，进而画图求解。

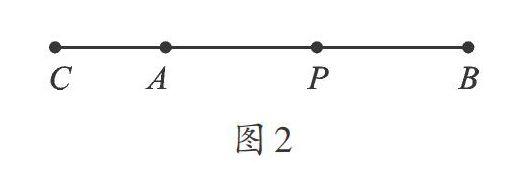
【正解】此题分两种情况：除了图1中点C是线段AB上一点外，还有一种情况，就是像图2那样，点C是线段BA延长线上一点，则有CP=AP+AC=3+2=5cm。

故正确答案为1cm或5cm。

例2 已知∠AOB=35°，以O为顶点作射线OC，并将∠AOB分为2：3的两个角。若射线OD是∠AOC的角平分线，则∠AOD=______。

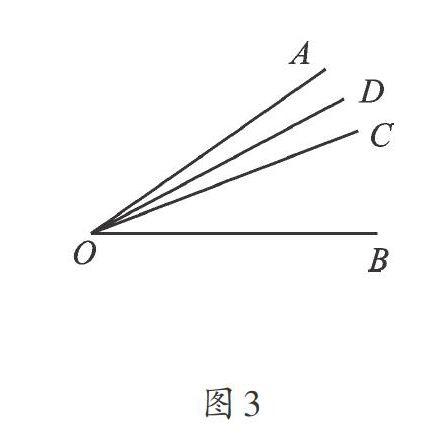
【错解】只考虑∠AOC：∠BOC=2：3，根据画出的图3，由∠AOB=35°，可得∠AOC=35°×2/5=14°。又因为OD是∠AOC的角平分线，所以∠AOD=1/2∠AOC=7°。

【分析】此题虽然没有出现例1中的“位置模糊”，却出现了“数量模糊”。错解忽略了讨论条件“OC将∠AOB分为2：3的两个角”中，∠AOC与∠BOC到底谁是2份，谁是3份的必要性。所以在解决此类问题时，不仅要关注条件中位置的不确定性，还要关注数量的不确定性，只有两方面都考虑到，才能不漏解。

【正解】此题分两种情况：除了图3中∠AOC：∠BOC=2：3，也可能像图4中那样，∠AOC：∠BOC=3：2，此时∠AOC=35°×3/5=21°，从而得到ZAOD=1/2∠AOC=10.5°。

故正确答案为7°或10.5°。