直流扰动下变压器绕组振动研究

刘子铭，苏 昊

(现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学)，吉林 吉林 132012)

直流扰动下，电力变压器的电感和电流会发生畸变，从而影响设备自身甚至电网的安全与稳定[1-3].直流扰动情况下的变压器，存在铁心饱和程度加深、励磁电流畸变、振动增大、铁心松动、绕组变形以及低频谐波增加等现象，会导致相关电气参数的保护故障以及补偿装置误跳等问题[4-8].因此，铁心-绕组构件抗直流扰动能力已成为电力变压器设计及运行所考察的关键指标[9-10].

变压器绕组振动是由流过电流的绕组在变压器漏磁中受到电磁力作用而引起的受迫振动[11-12].目前，国内外学者针对变压器绕组振动模型及振动特性问题开展了广泛的研究.文献[13]利用线饼轴向静压位移关系，建立绕组线饼轴向振动等效单自由度分析数学模型.文献[14]借助于所建立的换流变压器三维有限元模型，仿真得到换流变绕组受电磁力激励时的振动波形.文献[15]通过线性拟合的方法分析了温度对绕组和铁心振动产生、合成和传播的影响.综上所述，对于变压器振动问题的研究已取得众多成果，但对于交直流混杂情况下的变压器振动鲜有研究.

为研究交直流混杂情况下三相变压器绕组振动特性，本文建立变压器状态方程，根据能量平衡有限元法由电流计算该时刻的时域电感；利用高阶迭代计算时域电路；将求解得到的耦合参数分别代入磁场、电路模型循环迭代实现电磁耦合，并对电流参数进行辨识.在此基础上进行变压器绕组振动谐响应分析，得到振动加速度.对不同情况下的变压器进行仿真分析，并利用实验验证仿真结果的正确性.

1 变压器交直流混杂模式状态方程

建立基于电磁耦合模型的变压器直流入侵状态方程为

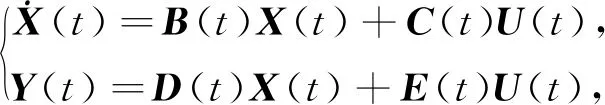
(1)

公式中：X(t)为系统状态变量，包含电流矩阵i和电感矩阵L；U(t)为系统输入变量，包括交流电压激励与直流扰动电压列向量；Y(t)为输出变量，主要包含电路参量与磁场场量；B(t)、C(t)、D(t)、E(t)为系数矩阵.该状态方程包含电路与磁场两个部分，其求解过程通过时域磁场-电路间接耦合实现.

1.1 基于磁场模型的电感计算

假定某一时刻的绕组电流已知，利用能量平衡有限元法(EBFEM)基于矢量磁位A计算该时刻的时域电感.

磁场模型为

(2)

公式中：μ为磁导率；J为电流密度矢量，表示绕组激励电流的分布情况.

通过伽辽金加权余量公式求解磁场模型：

(3)

公式中：{Mm}为权函数序列，权函数与基函数相同，m为权函数序列通项编号；en为边界面单位法向分量.将加权余量方程离散形成代数方程组，求解可得A，进而计算磁场场量B、H等.

根据能量平衡法，由系统能量计算时域电感.某一时刻任意两绕组电流变化为diη、diθ，可将变压器的电磁能量变化与状态变量关联，得到：

(4)

由能量守恒知，联立公式(3)可得到时域电感，以作为电路模型的状态变量.

图1 Y/Δ变压器直流扰动电路模型

1.2 基于电路模型的电流参数辨识

Y/Δ变压器直流扰动模型如图1所示.图1中，iA、iB、iC为高压侧绕组电流，ia1、ib1、ic1为低压侧端口电流，ia、ib、ic为低压侧Δ接绕组电流；L为自感，M为互感；r1、r2为绕组电阻；uA、uB、uC为高压侧电压，ua、ub、uc为低压侧电压；icn为低压侧环流；UDC为直流电压源.

推导Y/Δ变压器时域电路微分方程，并忽略各绕组自身漏感[16-17]：

(5)

将求得的tk时刻的电感参数代入公式(5)得到绕组电流ik，根据高阶改进欧拉法(HOIEu)由ik计算tk+1时刻的电流

(6)

公式中：h为步长；s为步长内的分段计算斜率列向量.

基于电磁耦合原理的状态方程求解过程如下：

(1)利用能量平衡有限元法在磁场模型中计算电感，并带入时域电路微分方程计算电流；

(2)将改进欧拉法求得的下一时刻电流回馈于磁场模型，计算下一时刻的时域电感;

(3)以此循环迭代求解.

2 振动谐响应模型

根据上述所得参数可建立变压器绕组振动谐响应模型，绕组单元电磁力为[18]

(7)

电磁力激励作用下的绕组振动满足动力方程：

(8)

公式中：M为模型质量矩阵；ε为模型阻尼矩阵；K为模型刚度矩阵；s(t)为模型节点位移向量.

对绕组所受的电磁力进行傅里叶变换，即可求得各谐波分量，将其作为简谐激励源，进行稳态结构谐响应振动分析.考虑材料刚度与简谐激励的频率，受力谐响应原理为

F1+jF2=(-ω2m+jωε+K)(s1+js2)，

(9)

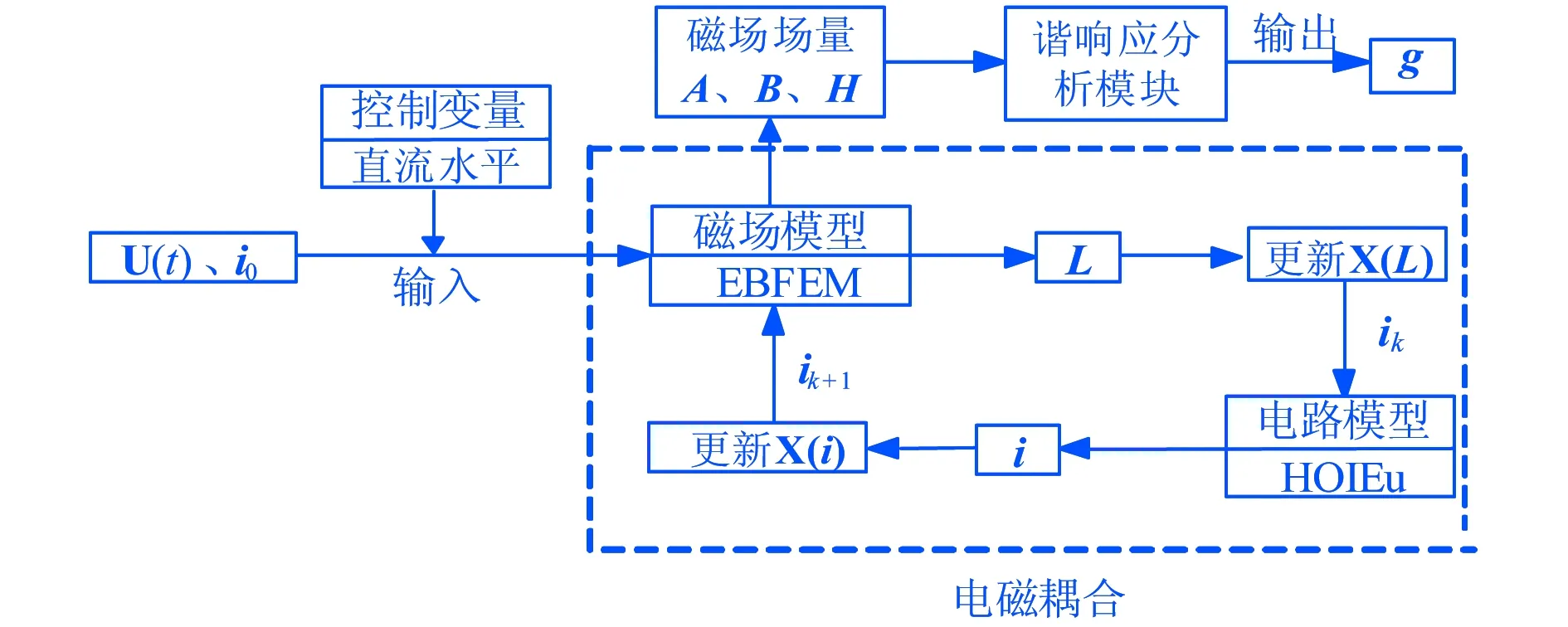
图2 振动谐响应原理

公式中：ω为简谐激励的角频率.

根据振动位移可得振动加速度

(10)

基于电磁耦合状态方程的振动谐响应原理如图2所示.

3 仿真分析

根据实际三相三柱式Y/Δ变压器BSS- 1000VA建立仿真模型参数，如表1所示.在一次侧接入直流电流源模拟直流扰动，计算其电磁特性.

表1 变压器参数

3.1 空载运行

一次侧接入直流电流源产生的直流电流为IDC(IDC=αI0)，其中α为直流水平系数，表征直流扰动的大小.分别对α=0、1.0、2.0、3.0四种直流扰动下的变压器运行模式进行仿真，考虑Y/Δ变压器的三相对称性，以A相为例，空载运行(负载率为零)时的一次侧绕组电流iA0和铁心平均磁通密度BA如图3所示.

(a)绕组电流iA0(b)铁心磁密BA图3 不同直流水平下的电磁参数

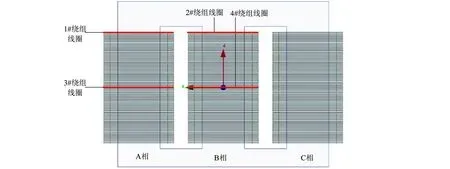
图4 Y/Δ变压器铁心-绕组结构

空载运行时，变压器绕组电流与励磁电流基本相同，如图3所示.当α=0时，iA0为尖顶波，当iA0处于波峰波谷时，铁心处于励磁饱和状态.在交直流混杂模式下，随着直流扰动程度加大，iA0畸变越大，波形正半周期畸变，负半周期衰减；铁心饱和程度加深.

根据三相对称性，选取变压器A、B相的端部与中部绕组进行分析，如图4所示.

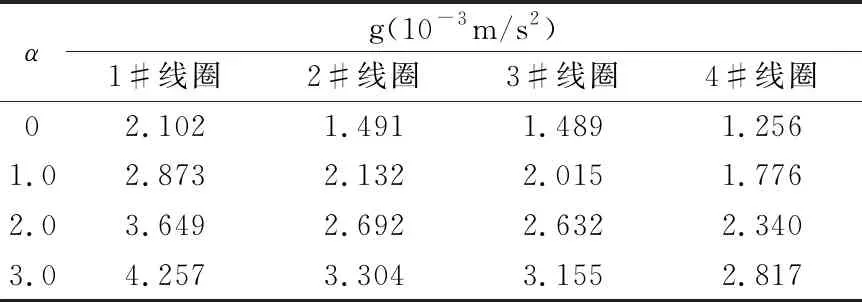
表2 不同直流扰动下的振动加速度

不同直流扰动下绕组振动加速度，如表2所示.

无直流扰动时，各绕组振动较小，随着直流水平升高绕组振动加速度逐渐增大.结合图3可以看出遭受直流扰动时电流畸变导致变压器铁心饱和，漏磁增大，振动加剧.其中1#、2#线圈振动加速度分别大于3#、4#线圈，说明各相端部线圈振动强于中部；1#、3#线圈振动加速度分别大于2#、4#线圈，表明边柱绕组振动强于中心柱绕组.仿真结果与文献[19]所得结论吻合.

对1#、3#线圈的振动加速度进行FFT变换，振动频谱结果如图5所示.

无直流扰动时，振动频谱中出现偶次谐波分量，归结其原因是铁磁材料磁滞伸缩效应.绕组的振动周期为电流频率的1/2，所以其振动基频为100 Hz[19].随着直流扰动加大，各谐波分量振动加速度均增大，低频分量所占比重较大，100 Hz处振动情况最为严重，说明直流扰动对绕组振动的基频分量影响较大.

3.2 负载运行

变压器负载运行时(70%负载率)，不同直流水平下变压器绕组电流iA如图6所示.

图6 负载运行不同直流水平下的iA

αg(10-3m/s2)1#线圈2#线圈3#线圈4#线圈04.5453.7063.6993.0241.04.8843.9683.9373.1682.05.2474.2604.2353.5073.05.6154.6994.6113.845

结果表明随着直流扰动水平升高iA波形畸变增大，由于负载运行时本身绕组电流数值较大，所以畸变程度较小.

不同直流扰动下的振动加速度，如表3所示.

由表3可知，1#、3#线圈振动加速度测量值分别大于2#、4#线圈；1#、2#线圈振动加速度测量值分别大于3#、4#线圈，且绕组振动加速度随着直流扰动水平升高而加大，与空载运行所得规律一致.但其测量值明显大于空载运行时所测数值，说明在相同直流扰动水平下，负载率越高振动越剧烈.

1#线、3#线圈振动加速度频谱图，如图7所示.

不难看出，随着直流扰动增大，各次谐波分量均逐步上升，变化规律与空载运行类似.通过分析变压器在不同运行方式遭受直流扰动的绕组振动加速度，可以归纳其规律：

(1)交直流混杂模式下变压器绕组振动幅度随直流扰动水平升高而愈发剧烈，且振动幅度端部线圈大于中部线圈、边柱绕组大于中心柱绕组；

(2)随着负载率增大，绕组振动幅度增大，但空载运行时绕组振动幅值变化更明显，说明负载率越低，其绕组振动受直流扰动影响越大.

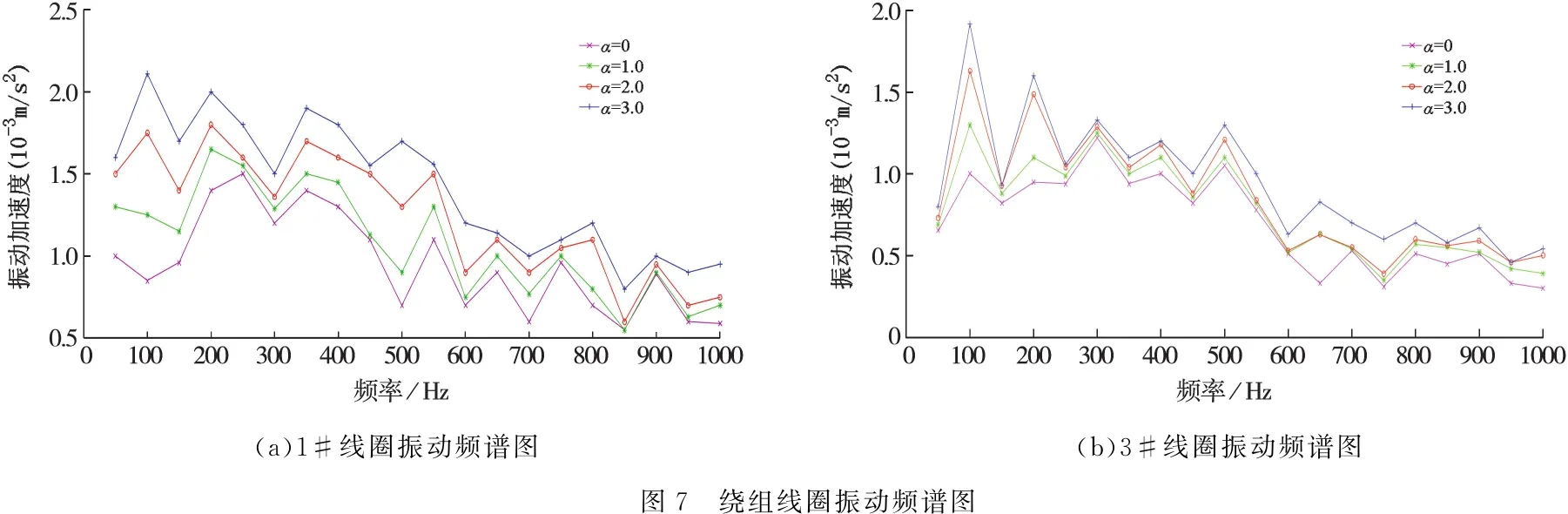
(a)1#线圈振动频谱图 (b)3#线圈振动频谱图图7 绕组线圈振动频谱图

4 动模实验

搭建模块化Y/Δ变压器交直流混杂运行实验平台，如图8(a)所示.实验变压器参数如表1所示.振动实验量测点的选择与仿真测试点分布保持一致，实验接线如图8(b)所示.

图8 动模实验平台

图9 空载运行不同直流水平下的iA0

αg(10-3m/s2)1#线圈2#线圈3#线圈4#线圈01.9961.4421.5591.2391.02.8092.0112.1091.2402.03.6852.6432.7102.3483.04.3823.2873.2232.811

图8(a)中①为振动监测模块，②为电流监测模块，③为电压调节模块，④为直流注入模块.具体实验步骤如下：

(1)转动三相调压器T1，将变压器一次侧的线电压调整到380 V;

(2)闭合直流支路开关K，调节滑动变阻器Rd进而改变直流电压源UDC注入直流的大小;

(3)观测、记录示波器中电压、电流波形;

(4)在振动监测模块中使用压电加速度传感器JF2100-T测量不同直流扰动下的各线圈的振动信号.

4.1 空载运行

空载运行时不同直流水平下的iA0，如图9所示.

无直流扰动时，iA0呈现为尖顶波.注入直流后，α值越大，铁心饱和程度越深，空载电流波形越尖，即波形畸变越严重，与仿真结果一致.

各线圈的振动加速度，如表4所示，1#、3#线圈振动频谱，如图10所示.

(a)1#绕组振动频谱图(b)3#绕组振动频谱图图10 绕组线圈振动频谱图

图11 负载运行不同直流水平下的iA

随着直流扰动水平增高，各线圈振动加速度增大，且1#、3#线圈分别大于2#、4#线圈，1#、2#线圈分别大于3#、4#线圈.频谱图中可见，低频分量占据较大比重，振动加速度在100 Hz处最大，与仿真分析所得结果一致.

4.2 负载运行

变压器负载运行时，(70%负载率)A相绕组在不同直流扰动下的一次侧电流iA，如图11所示.

无直流扰动时电流呈现正弦波，当注入直流后电流波形畸变，但是其变化程度明显小于空载电流，说明空载运行时直流扰动的影响更大.

不同直流扰动下振动加速度，如表5所示.绕组线圈振动频谱图，如图12所示.

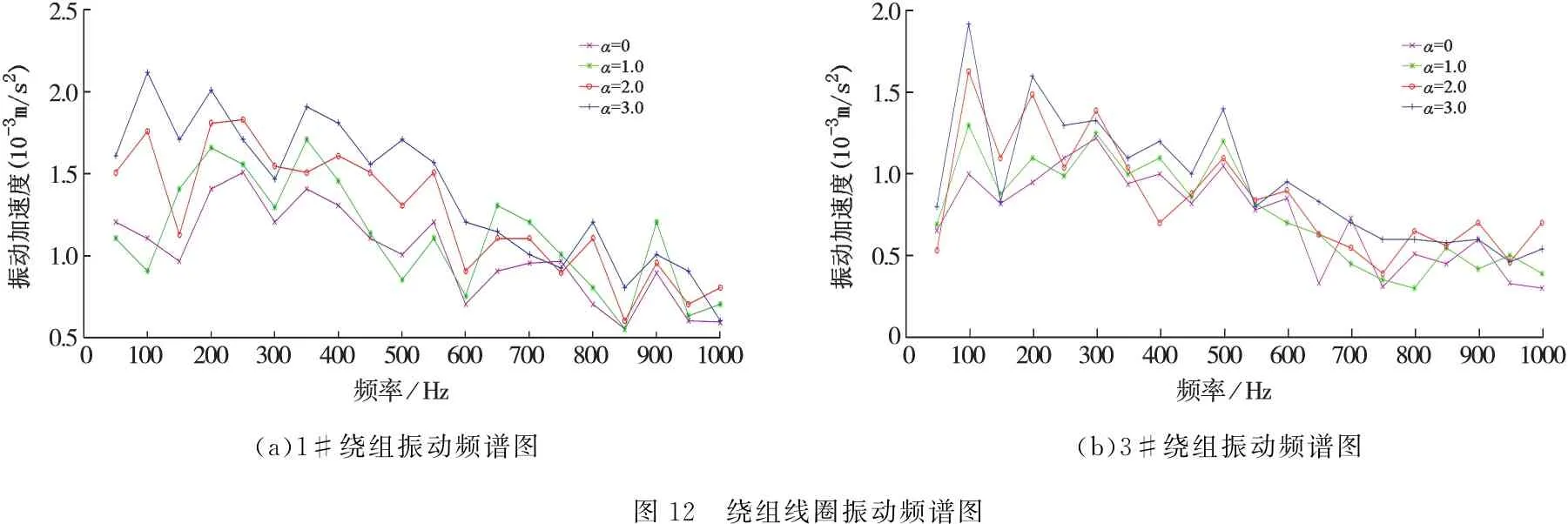
(a)1#绕组振动频谱图(b)3#绕组振动频谱图图12 绕组线圈振动频谱图

随着α值增大，各线圈振动加速度增大，在注入相同直流时，负载运行时线圈振动加速度大于空载，但空载运行时的变化幅度更为明显.对比实验与仿真振动频谱图，发现实验所得频谱图较为杂乱，是由于实测过程中的设备误差与人员误差，但总体规律与仿真结果一致.

5 结 论

对于三相变压器在交直流混杂模式下的绕组振动问题，得出以下结论：

(1)直流扰动越大，铁心饱和程度越深，空载电流波形畸变越严重，绕组振动越剧烈；且边柱绕组振动情况强于中心柱绕组，各端部绕组强于中部.振动频谱中低频分量所占比重较大，直流扰动对基频分量(100 Hz)的影响最为强烈.

(2)变压器负载运行时的绕组振动幅度更大，但空载运行时振动变化更加明显，说明变压器负载率越低所受直流扰动影响越大.