蜗卷弹簧缺陷影响超声导波模态变化的辨识

赵淳，易晓旭，华帅，覃小倩，毛汉领

(广西大学 机械工程学院，广西 南宁 530004)

0 引言

蜗卷弹簧是广泛应用于机械结构的储能核心元件，在经过长期服役后很容易在弹簧表面或内部出现疲劳裂纹等损伤，因此，对蜗卷弹簧早期疲劳裂纹等缺陷进行无损检测非常重要。

超声周向导波特别适用于蜗卷弹簧这类定周长检测距离的曲面结构缺陷的识别和定位，但导波检测得到的信号为瞬态信号，属于非平稳随机信号。因此，提高超声导波信号的分析和处理能力是提高缺陷辨识精度的重要手段。CHO等[1]通过对不同热负荷铝管试样导波检测信号进行快速傅里叶变换，从频谱中提取高次谐波信息，利用超声导波的声学非线性参数检测管状结构的热损伤。周正干等[2]通过对铝板和蜂窝板的导波信号进行短时傅里叶变换和时频谱分析，得出导波的传播距离较远时，利用短时傅里叶变换不仅可以得到信号动态的频谱分析以及模式识别，还能较精确地测量其实际群速度。张磊等[3-4]为有效获取断轨的超声导波信号，提出一种新的小波阈值函数以改善降噪效果，通过比较，新阈值函数法去噪后信噪比比软阈值函数法提高了6 %～15 %，比硬阈值函数法提高了8 %～25 %。FENG等[5]设计了一种适合用于现场钢绞线缺陷检测的仪器，并根据检测到的纵向超声导波信号的短时傅里叶变换结果，分析缺口缺陷对L(0,1)和F(1,1)模式之间转换程度和缺口反射信号幅度的影响，由此证明设计的仪器具有较高的检测性能。

ZHOU等[6]利用L(0,2)模式导波对弯管周向裂纹进行检测，通过用母小波为db1的三重小波分解和重构对信号进行去噪，提高了回波信号的检测灵敏度。BENJAMIN等[7]对疲劳裂纹进行导波检测，并利用二维快速傅里叶变换分析其导波输入和输出信号，从而实现导波模态识别。TSE等[8]通过磁致伸缩超声导波方法对由于腐蚀和疲劳导致的钢丝绳进行状态检测，对得到的微弱损伤信号进行小波分析，成功识别和表征缺陷的位置。DAI等[9]采用Wigner-Ville时频分析方法计算稀疏压电制动器的超声导波信号，并对比传统希尔伯特包络和Gabor小波变换的方法，说明了Wigner-Ville时频分析方法相对于一维结构具有更高的损伤定位精度。王国锋等[10]利用Morlet小波时频分析等方法对仿真和实验信号进行处理分析，验证了超声导波对H型钢结构损伤识别的可行性。SHARMA等[11]提出小波变换和匹配滤波技术相结合的小波匹配滤波技术，该技术能够在很大的噪声中对较小的损伤信号进行识别，显著提高了滤波信号的精度。CHENG等[12]通过希尔伯特变换计算管道导波回波信号的包络图，提高了管道检测缺陷定位和识别的精度。DA等[13]提出了一种波数域小波变换的去噪方法，并通过实验验证波数域小波变换比时域去噪效果更好。陆希等[14]通过利用连续小波变换以及希尔伯特变换对兰姆波信号进行处理，将与损伤有关的时域特征从中提取了出来。张海燕等[15]通过将希尔伯特黄变换、快速傅里叶变换与小波变换这三种方法在时频分辨率方面对比，得出希尔伯特黄变换的时频分辨率更高，并且适用于兰姆波信号分析。赵振宁等[16]采用双重时间尺度对比对薄板兰姆波模态进行分析，结合二维傅里叶变换以及希尔伯特黄变换等信号分析方法对实验数据进行分析，证明了这些方法可以识别兰姆波导波模态并获得较高的时间分辨率。

采用超声周向导波检测蜗卷弹簧表面的轴向缺陷，可以得到包含缺陷和端面回波的导波信号，然而对于非平稳的导波信号，传统的信号分析方法无法解决信号的时间和频率同时表达的问题，从而不利于识别导波模式和定位缺陷。针对此问题，本研究首先基于超声周向导波检测方法对蜗卷弹簧表面的轴向缺陷进行检测，得到包含缺陷和端面回波的导波信号。再利用连续小波变换对蜗卷弹簧导波信号进行处理，得到导波信号的小波系数图，进而确定信号各频率成分的分布特点。通过小波变换幅度分布图提取小波幅度包络图，计算蜗卷弹簧内导波传播的主要模态，并观察导波模态转换现象，对缺陷影响导波模态及变化进行辨识。

1 连续小波变换局部分析原理

(1)

则称ψ(t)为基本小波或者母小波。

将母小波ψ(t)进行伸缩和平移可得到一个小波序列

(2)

式中：a为尺度因子，b为平移因子，ψa,b(t)为参数a和b的小波基函数。对于a，b均为连续的情况，又称为连续小波基数，它们是由同母小波ψ(t)经伸缩和平移后得到的。

将L2(R)空间任意函数f(t)在小波基下进行展开，得到函数f(t)的连续小波变换

(3)

式中：a，b和t均为连续变量；Wf(a,b)为小波变换系数。

由连续小波变换的原理可知，小波变换属于一种积分变换。小波变换对函数f(t)在小波基上的展开具有多分辨率的特性，这种特性正是通过尺度因子a和平移因子b得到的。根据a和b的不同，可以得到小波变换下不同时、频宽度的信息，从而实现对信号f(t)的局部化分析。

2 蜗卷弹簧周向导波检测实验

蜗卷弹簧周向导波检测实验系统如图1(a)所示，主要由RAM-5000-SNAP系统、计算机、示波器、负载电阻、衰减器和一个超声导波斜探头组成。为了降低实验误差和环境影响，采用一个探头自激励自接收的方式检测，斜探头中心频率为1 MHz，角度为64°，通过具有一定频率和特定角度的探头可在弹簧中激励出特定的导波模态，以降低信号分析的难度。探头方向沿着蜗卷弹簧周向，从外端面向内端面方向激励周向导波。实验对象为有两个轴向预置缺陷的蜗卷弹簧外圈结构，如图1(b)。探头布置如图1(c)所示，蜗卷弹簧外圈周长900 mm，轴向宽120 mm，厚度10 mm，距离外圈端面周向400 mm和600 mm处分别有两个轴向长3 mm、宽1 mm、深0.5 mm的预置缺陷，两个缺陷距离弹簧同一侧面的距离都是40 mm。为降低周向导波的频散，采用10个周期的正弦波作为激励信号，如图2。蜗卷弹簧材料为51CrMoV4，属于中碳合金钢，其横、纵波速分别为3 230、5 920 m/s。通过其尺寸和材料参数可以计算得到蜗卷弹簧导波传播的群速度频散曲线，如图3，图中按出现的先后顺序标出了前10个模态的周向导波。

(a) 实验系统示意图

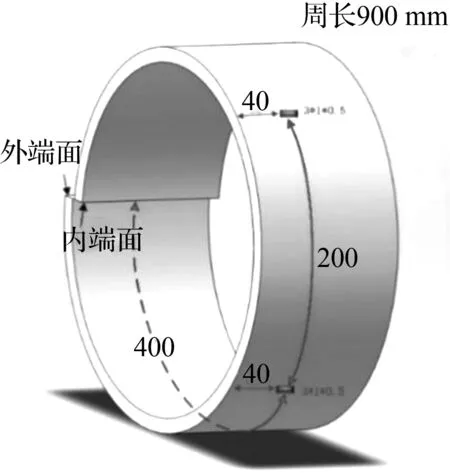
(b) 蜗卷弹簧外圈缺陷分布

(c) 探头布置图

(a) 激励信号时域图

(b) 激励信号频谱图

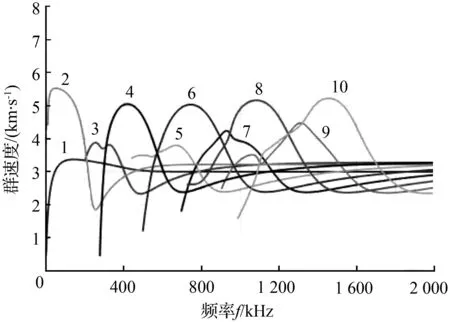
图3 蜗卷弹簧外圈群速度频散曲线Fig.3 Outer lap dispersion curve of coil spring

实验中，将探头分3个区域放置，分别对600 mm处单个缺陷区域的检测、400 mm和600 mm处两个缺陷区域的检测以及对非缺陷区域的检测，对3个区域检测都通过改变探头与缺陷的距离来分析导波回波信号。探头的分布如图1(c)，对600 mm处单个缺陷的检测，将探头分别放置于距外端面周向距离400 mm和500 mm位置处。对于400 mm和600 mm两个缺陷的检测，将探头分别放置于距外端面周向距离200 mm和300 mm位置处。对于蜗卷弹簧非缺陷区域的检测，将探头分别放置于与缺陷轴向距离为40 mm，与外端面距离为400 mm和700 mm的两个周向位置处。

对于600 mm处单个缺陷的检测，400 mm和500 mm位置处探头接收的导波回波信号波形如图4。对于两个缺陷区域的检测，200 mm和300 mm位置处的探头接收的回波信号波形分别如图5。对于非缺陷区域的检测，在400 mm和700 mm位置处传感器接收的回波信号波形分别如图6。通过两个位置处的传感器接收回波信号的时间差和两传感器的距离即可计算出导波在蜗卷弹簧中的传播速度，将其与导波群速度对比即可以确定在弹簧中传播的主要的导波模态。通过该模态群速度和缺陷回波时间可以计算出缺陷和激励传感器的距离，由此来实现周向导波对蜗卷弹簧缺陷的定位。但由接收信号波形图可看出，回波时域信号尤其是端面回波时域信号频散程度很大，难以确定端面回波时间，这会导致计算得到的群速度误差很大，不利于导波模式的识别和缺陷的定位。

(a) 400 mm处接收波形

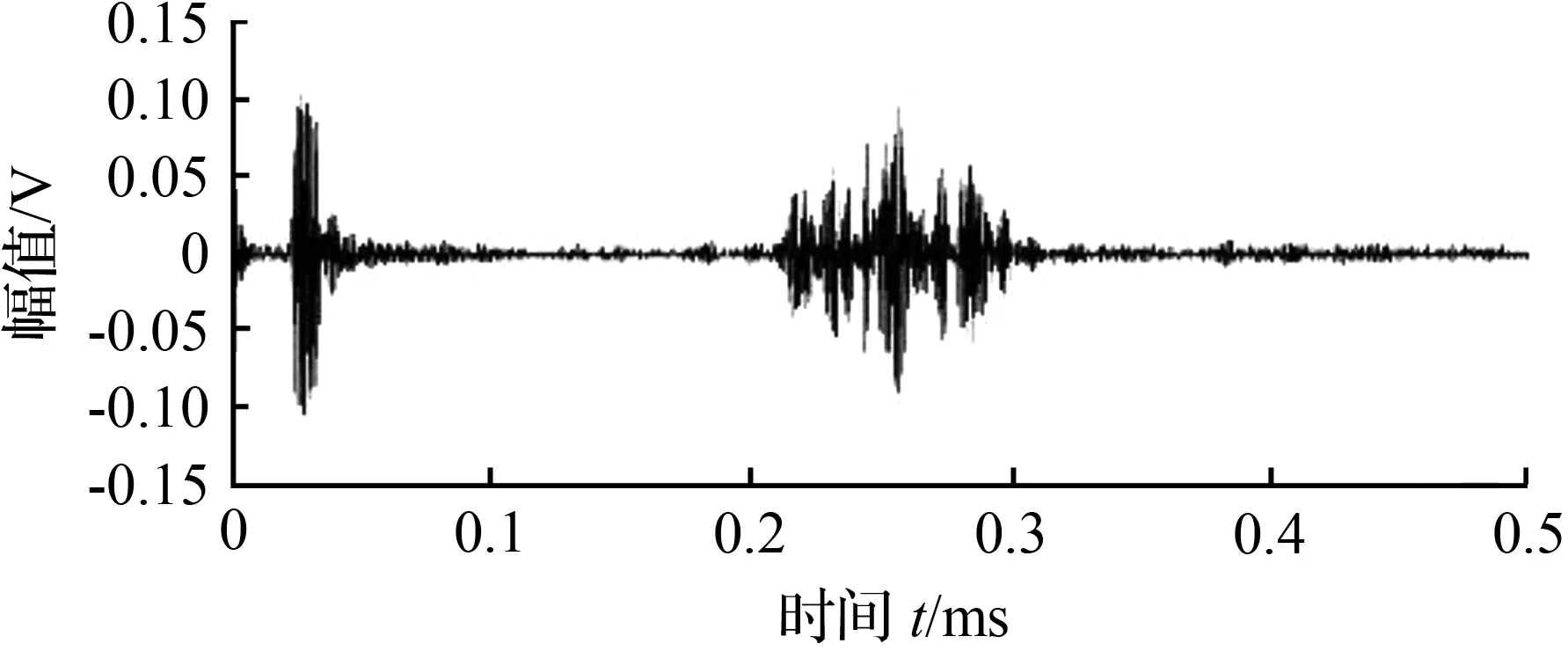
(b) 500 mm处接收波形

(a) 200 mm处接收波形

(b) 300 mm处接收波形

(a) 400 mm处接收波形

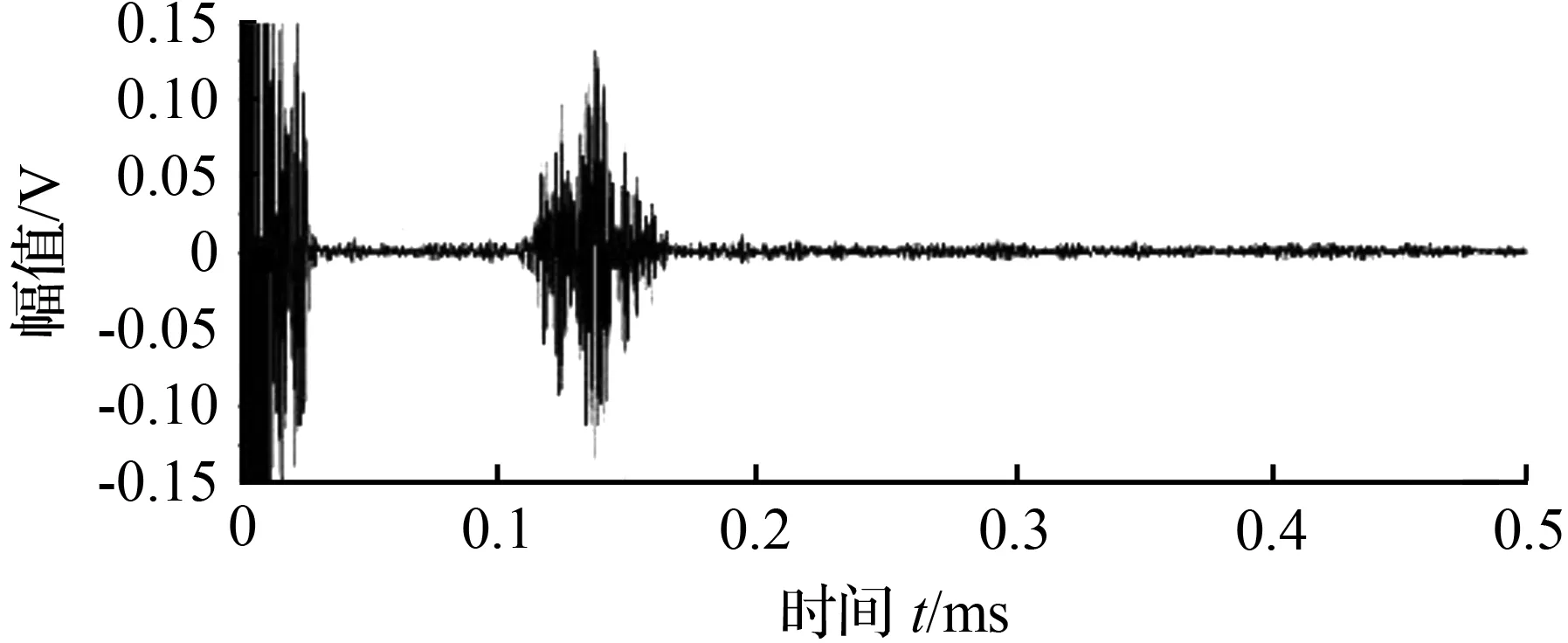
(b) 700 mm处接收波形

3 基于连续小波变换的模态识别方法

时域信号只能反映信号的幅值随时间的变化关系，很难明确信号的频率组成和各频率分量的大小，利用傅里叶变换对导波时域信号进行频谱分析可以得到时域信号的主要频率信息。以一个缺陷区域550 mm探头接收波形为例，利用傅里叶变换对该时域波形进行分析得到其频谱图如图7。通过傅里叶变换求得其他区域接收信号的频谱图与550 mm处的频谱图相似，在此不一一列举。由图7可以看出，对比激励信号频谱图，接收信号在3 MHz处产生了一个新的高频信号。由此可知导波在蜗卷弹簧中传播的信号频率成分除了1 MHz主模态的频率外，还产生了一个新的频率成分，由此可推断导波在传播过程中由于导波的频散特性发生了模态转换的现象，从而产生了一个具有新频率的模态。

图7 550 mm处接收信号频谱图Fig.7 Spectrum of received signal at 550 mm

傅里叶变换只能从频域上观察导波的频率，而小波变换具有同时在时域和频域表征信号局部特征的能力。针对研究的导波信号，需要小波母函数具有良好的频域特性。dbN小波系是工程上应用很多的小波函数，其特点是随着序号N的增大，时域集变长，时间局部性变差；同时正则性增加，频域局部变好。但是当N增大到10以后，dbN小波在频域内的分频表现与N=10时很接近，综合考虑在时频两域内进行分析的需要，以及导波具有频散特性的特点，选用db5母小波对蜗卷弹簧导波信号进行计算分析，小波尺度长度序列为256。选取每个区域中的一个时域信号计算小波变换结果如图8。从3个小波系数图可以定性看出，导波信号主要由2个时域分布不同的主成分组成，频率较低的成分1始终出现在整个信号段，是导波传播的主要成分，对应于傅里叶变换频率为1MHz的信号成分，频率较高的成分2是在导波传播遇到缺陷或者端面时出现，对应了傅里叶变换中产生的3MHz的高频成分。由此可知，通过频谱图和小波变换系数图可以确定缺陷信号的主要频率成分以及各成分的分布特点。

(a) 550 mm处小波系数图

(b) 350 mm处小波系数图

(c) 750 mm处小波系数图

连续小波变换包络图是导波回波信号能量在频率、时间和模态的分布，通过分析小波变换包络图可以计算导波传播的主要模态，观察导波的模态转换现象。

为了得到小波变换包络图，分别计算了各个接收信号连续小波变换绝对幅度的时频分布，以单个缺陷区域550 mm处导波信号的小波变换绝对幅度图为例，如图9(a)。图中可以清楚地观察到小波变换幅度随时间频率的空间分布情况，通过提取特定频率即斜探头中心频率1 MHz频率分量上的小波变换绝对幅度图可以得到该频率下小波变换的幅度包络图，如图9(b)。

(a) 550 mm处小波变换绝对幅度的时频分布

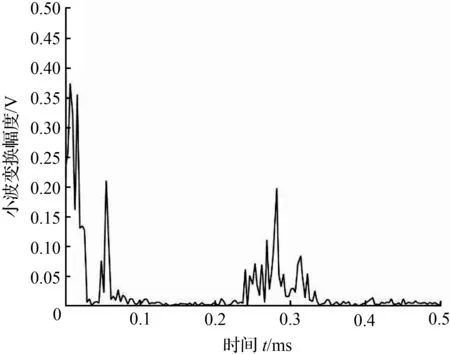
(b) 1 MHz频率下550 mm处小波变换幅度包络

由图9(b)可以得到波包1和波包2的传播时间分别为0.048 0、0.054 4 ms，结果见表1。通过计算波速和导波传播群速度对比可知，波包1和波包2分别对应导波的第2和第1个模态，同样的波包3和波包4也分别对应导波的第2和第1个模态。通过波包2和波包4的幅值可知导波信号在蜗卷弹簧中传播主要模态为第1模态。也说明了导波在传播过程中在遇到缺陷或者端面时，从第1模态转换为速度更快的第2模态，即在缺陷或端面区域产生了模态转换的现象。同理，对于其他点的导波信号也可以通过对比波包的理论群速度和实际群速度观察是否存在模态转换的现象。

表1 1 MHz频率下550 mm处信号波包速度Tab.1 Signal packet velocity at 550 mm at 1 MHz frequency

4 结论

① 本研究利用周向导波检测方法对蜗卷弹簧进行检测，通过改变探头与缺陷的距离获取和分析了600 mm处单个缺陷区域、400 mm和600 mm处2个缺陷区域以及非缺陷区域，这3个区域的导波回波信号。

② 采用连续小波变换法分别计算蜗卷弹簧3个缺陷区域回波小波系数，通过频谱图和小波变换系数图可以确定缺陷信号的主要频率成分以及各成分的分布特点。

③ 通过分析不同缺陷情况下小波变换幅度在时频空间的分布情况，截取1 MHz频率分量上的小波变换幅度图，通过对比波包的理论群速度和实际群速度可知，蜗卷弹簧内传播的导波存在模态转换的现象，且模态转换现象多存在于缺陷和端面等结构不连续处。