悬浮隧道波浪作用下弹振工程分析方法研究
周卓炜 ,林巍 ,刘傲祥 ,张宁川
(1.中交悬浮隧道结构与设计方法研究攻关组,广东 珠海 519000;2.大连理工大学,辽宁 大连 116024;3.中交公路规划设计院有限公司,北京 100088;4.大连元堃海洋科技有限公司,辽宁 大连 116000)
1 概述
拉锚式悬浮隧道在周期性环境荷载作用下,管体将产生相应的周期性往复运动,进而引起缆索伸长量的改变,可能发生缆索松弛。当缆索松弛态与张紧态相互转变时,可能使得缆索承受较大张力,对缆索造成不利影响,甚至可能导致缆索破断[1]。该现象称为弹振现象,对悬浮隧道安全影响大,悬浮隧道的设计应避免弹振的发生。
Seo等人在研究缆索弹振问题时,考虑八字形布缆方案(图1(a)),采用Morison方程求解波浪力,仅考虑静力作用,忽略缆索和管体的动力响应,通过判断缆索张力是否为0,从而给出简单快速的弹振判断式[2]。Lu等人考虑交叉四斜布缆方式(图1(b)),采用Morison方程求解波浪力,采用线形方法及小位移假定,解析求解了管体在波浪作用下的位移并转化为缆索伸长量变化,通过与缆索初始伸长量对比,判断缆索是否发生弹振[3-4]。Hong采用该判断模型给出了悬浮隧道浮重比和缆索弹振的关系图[5]。Budiman等针对交叉布缆方式(图1(c)),通过节段水槽试验给出了缆索发生弹振时的缆索张力变化以及缆索发生弹振的预测统计表[6]。

图1 悬浮隧道缆索弹振问题研究中的缆索断面布置形式Fig.1 Lineslayout in thestudy of slack and snap problems of SFT lines
本文针对悬浮隧道结构与设计方法讨论弹振问题研究方法,涉及悬浮隧道的初期净浮力设计(或浮重比取值)、后期结构验算以及锚固基础的强度设计等。本文与之前研究结果比较见表1。以下从弹振研究方法、悬浮隧道初期设计的净浮力快速计算以及结论与展望等方面展开。

表1 各弹振研究横向对比Table1 Lateral comparison of theslack and snap studies
2 悬浮隧道设计弹振研究构想
2.1 弹振研究思路
在环境荷载作用下,当缆索张力为0时(或缆索相对无应力状态伸长量为0时),缆索处于松弛状态,之后可能发生弹振。悬浮隧道缆索运动取决于管体运动。
悬浮隧道弹振研究流程及可选方法见图2。通过悬浮隧道管体动力分析,将获得的管体位移及缆索张力信息反馈到缆索上,当不考虑缆索垂度效应时,将管体位移和张力通过刚体运动关系转化为缆索信息代入缆索弹振判断条件,判断是否发生弹振;当需要考虑缆索垂度效应时,对缆索进一步开展动力分析,获取缆索详细信息进行弹振判断。判断弹振不发生时,认为悬浮隧道设计合理;判断发生弹振时,需要更改悬浮隧道设计并重新进行弹振分析。

图2 悬浮隧道弹振问题研究流程Fig.2 Research processof slack and snap problemsin submerged floating tunnel
2.2 管体动力分析方法
假定管体运动为小位移变化,运动过程中缆索刚度不变,研究管体动力的分析方法有[8]:
1)Ansys MFX全耦合分析。采用Ansys MFX模块建立悬浮隧道节段模型,进行全耦合求解,该方法精度高,但计算资源占用大、效率低。
2)Morison方程耦合Ansys动力计算。采用Morison方程求解波浪力,将波浪力信息加载到Ansys结构计算模型中进行动力计算。
3)解析方法。基于线形假定和节段真实刚度解析求解悬浮隧道节段位移。
2.3 缆索动力分析方法
缆索动力分析方法用于获取缆索张力信息或者获取缆索伸长量信息,判断缆索是否发生弹振。对于不考虑垂度的张紧线,缆索采用线形方法简单分析即可。针对悬链线和考虑垂度的张紧线,Vassalos等总结了4种分析缆索动力特性的主要方法[1]:
1)有限差分法。分析控制缆索运动的双曲方程,采用有限差分方法在时域范围内近似求解。
2)伽辽金方法。该方法假定解为一系列基模态的叠加,利用了缆索的光滑结构。
3)集中质量法。采用集中质量法后控制方程变为常微分方程,从而可以采用数值积分。
4)解析方法。由于非线性和控制方程的耦合特性,解析解仅适用于简化模型问题。
3 悬浮隧道缆索弹振判断方法研究
以图1(d)所示缆索布置形式为例提出适用于张紧式缆索的坐标转换弹振判断方法(坐标法),在设计流程中的作用见图2。假定锚固基础不变位,且管体运动位移较小。设管体水平向位移、竖直向位移、转角位移依次为δx、δz、δa,以顺时针为正。不考虑缆索垂度效应影响,以管体中心为原点建立坐标系xoz,A、F、G、E四点为锚固基础位置,假定运动过程中不变,B、D为缆索与管体的连接点。根据几何关系得到各点坐标如下:

根据各点坐标可以算出当管体发生δx、δz、δa运动时的缆索长度,分别记为LBA、LBF、LDG、LDE。记静水时(δx=δz=δa=0)缆索的初始长度为 LBA0、LBF0、LDG0、LDE0,各缆索静水时的初始伸长量为 Ti/ki。则各缆索不发生弹振的判断式为:

式中:TBA0、TBF0、TDG0、TDE0分别表示各条缆索的初张力;kBA、kBF、kDG、kDE分别表示各条缆索的刚度,并假定在管体运动过程中,缆索刚度不变。仅当式(1)至式(4)均满足时,缆索不发生弹振。
4 临界净浮力快速判断
除非另有物模研究支撑,悬浮隧道设计最初就需要通过弹振计算最小净浮力来指导横断面的拟定。作者推导了基于弹振判断的最小临界净浮力快速判断公式。
4.1 不考虑缆索垂度效应的临界净浮力计算式
以图1(d)中缆索BA为例,长度和初张力分别为:

记α为缆索分担的净浮力系数,H为锚固断面间距,ΔB为悬浮隧道管体净浮力,则有:

结合式(6)和式(7),可以得到临界净浮力计算式为:
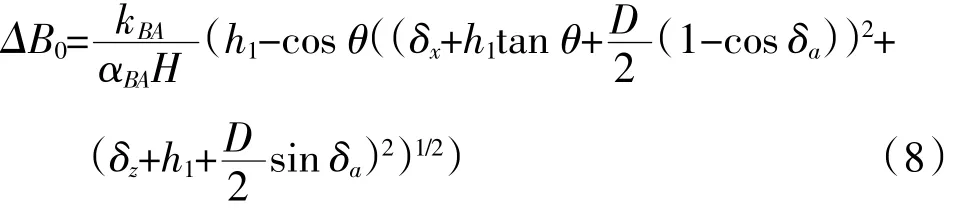
仅当悬浮隧道净浮力ΔB大于临界净浮力ΔB0时,缆索不发生弹振。
将式(8)进行扩展,得到任意缆索对应的临界净浮力计算式为:

式中:ΔB0i表示导致第i条缆索发生松弛的临界净浮力;ki表示第i条缆索的刚度;αi表示第i条缆索的净浮力分配系数;H表示锚固断面在悬浮隧道纵向上的分布间距;hi表示第i条缆索与悬浮隧道管体连接点到海底的距离;θi表示第i条缆索与竖向线的夹角;φi表示第i条缆索方向角(缆索方向角定义为以管体上锚点为圆心按逆时针方向旋转到竖直线上的角度,如图 3);δx、δz、δa分别表示管体在x、z方向的平动位移以及转角运动量;gix(δa)、giz(δa)分别表示由于管体转动位移引起的第i条缆索与管体连接点在x和z方向上的位置变化。
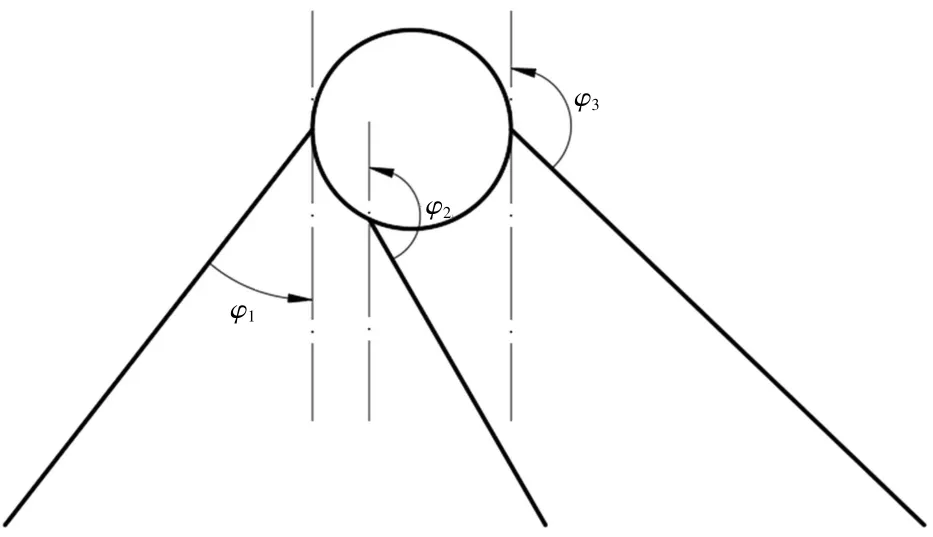
图3 缆索方向角示意图Fig.3 Cable direection angle
当δa=0时,gix(δa)、giz(δa)均为0。δa以顺时针方向为正。当悬浮隧道横截面为圆形(直径为D),且缆索与管体的连接点与圆心处于同一高度处时,gix(δa)、giz(δa)形式如下:

当锚点位于图4(a)所示的管体上半区域(含左端点)时,式(10)取“+”计算;当锚点位于图4(a)所示的管体下半区域(含右端点)时,式(10)取“-”计算;当锚点位于图4(b)所示的管体左半区域(含下端点)时,式(11)取“+”计算;当锚点位于图4(b)所示的管体右半区域(含上端点)时,式(11)取“-”计算。

图4 扭转引起的位移正负判断图示Fig.4 Judgment of positive or negative displacement caused by torsion
4.2 悬浮隧道真实刚度
缆索刚度可以根据式(12)计算:

式中:EA为缆索的抗拉强度;li为第i条缆索的长度。由缆索引起的管体等效刚度为:

参数含义同前。
将悬浮隧道模型简化为弹性地基梁模型,对于两端固结的悬浮隧道,管体真实刚度为:

式中:Kh表示管体水平方向真实刚度;Kv表示管体竖直方向真实刚度;EIx、EIz分别表示悬浮隧道x、z向抗弯刚度;LS表示悬浮隧道长度,其余参数含义同前。
4.3 波浪作用下缆索临界净浮力快速计算式
当悬浮隧道环境荷载为波浪荷载时,忽略悬浮隧道扭转效果,采用线性化方法对波浪力和回复力进行简化,假定结构运动速度相比水体运动速度较小且可忽略,假定结构发生小幅度位移,缆索刚度考虑为定值,由此得到波浪作用下任意时刻管体在x、z方向运动位移增加量的解析表达式为[4]:

式中:各项参数详见文献[4],考虑管体真实刚度(式(15)和式(16)),推导得到波浪作用下管体在x、z方向运动位移的快速计算式(式(19)和式(20),推导过程略)。

将时间t等间距(间距为Δt)离散为一系列时间点。则波浪作用下任意时刻管体在x、z方向上的运动位移为:

式中:N表示总计算时间点数。在波浪作用下,取

式中:M为波浪周期倍数;Tw为波浪特征周期;为向上取整符号。对于规则波,Tw为波浪平均周期,建议取M=20;对于不规则波,Tw为波浪谱峰周期,建议取M=100。
将式(19)、式(20)、式(21)和式(22)代入式(9)中,得到波浪作用下不考虑缆索垂度效应的临界净浮力快速计算式为式(24)。

式中:ΔB0i为波浪作用下不考虑缆索垂度效应时导致第i条缆索松弛的临界净浮力;ΔB0it(t=nΔt)为任意时刻t下以第i条缆索参数计算的发生松弛的临界净浮力;kw为波浪特征波数;ω为波浪特征圆频率(如谱峰频率);m为管体每延米质量;CM为管体附加质量系数;ρw为水体密度;A为管体横断面面积;h0为管体横断面中心点到海底的距离;d为悬浮隧道安装位置特征水深;D为隧道轴向上每延米管体的过流断面面积(如横断面为圆形,则D为圆直径);CD为管体拖曳力系数;Hw为波浪特征波高(如有效波高);其余参数含义同前所述。符号MAX表示取一组数中的最大值,n=0,1,2,3,…,N,计算所有时刻的ΔB0it(t=nΔt),并将其中的最大值作为ΔB0i。
4.4 算例
以规则波及图1(d)所示缆索布置方案为例:图1(d)中各缆索从左到右依次编号为1、2、3、4,波浪平均周期Tw=13 s,平均波高Hw=20 m,水深d=70 m,波浪特征圆频率通过波浪周期计算,ω=0.483 rad,波浪特征波数按照线形色散关系求得kw=0.025 2,各缆索在隧道上锚点到海底距离hi=32.36 m,隧道总长LS=2 000 m,隧道x向抗弯刚度EIx=3.67×1013N·m2,隧道z向抗弯刚度EIz=3.81×1013N·m2,管体横断面中心点到海底的距离h0=hi,各缆索与竖直线的夹角θi依次为60°、0°、0°、60°,水密度 ρw=1 000 kg/m3,隧道外直径 D=15.28 m,流体拖曳力系数CD=1.2,流体附加质量系数CM=1,隧道横断面几何面积A=183.37 m2,隧道每延米质量m=107 744 kg,隧道纵向缆索布置间距H=100 m,各条缆索净浮力分配系数αi依次为0.25、0.25、0.25、0.25,各缆索方向角φi依次为 60°、0°、0°、120°。时间间隔 Δt=0.2 s,M=20,则 N=1 300。
将以上参数代入式(24)中,计算得到最大临界净浮力为ΔB0i=794 882.14 N。采用Ansys软件建立悬浮隧道整体动力验算模型,计算得到隧道运动位移,代入式(9)中进行弹振验算,得到悬浮隧道缆索发生弹振的临界净浮力ΔBANSYS=827 284.58 N。本文推导的快速计算方法得到的临界净浮力相比Ansys模型计算位移结果转换的临界净浮力偏小3.9%,偏差较小。因ΔB0i<ΔBANSYS,为保证设计安全,本算例需加大设计净浮力重新设计悬浮隧道。
5 结论与展望
本文提出悬浮隧道波浪力作用下弹振工程问题的研究流程构想,并以两竖两斜缆索横断面布置形式为例,推演了特定缆索是否发生弹振的判断式;并考虑设计实际问题,弹振判断式推广到任意悬浮隧道缆索是否发生弹振的快速判断式进而指导设计最初横断面拟定时的最小净浮力的参考值。
当前研究可覆盖单向规则波和不规则波作用下弹振问题,需要进一步研究多向不规则波对弹振分析结果的影响。
——垂度法

