悬浮隧道多锚固方案结构综合分析与评价研究
刘傲祥 ,林巍 ,尹海卿 ,刘凌锋
(1.中交悬浮隧道结构与设计方法研究攻关组,广东 珠海 519000;2.大连元堃海洋科技有限公司,辽宁 大连116000;3.中交公路规划设计院有限公司,北京 100088;4.中交第三航务工程局有限公司,上海 200032)
0 引言
悬浮隧道总体可分为浮筒式、锚索式、混合式以及自由式[1-2],前两者相对较常见。其中,自由式概念通常适用于较短悬浮隧道,也有通过拱式纵向线形实现数公里长无沿程锚固悬浮隧道的方案概念[3]。浮筒式悬浮隧道管体通过刚性竖向连接与水面上浮筒连接,如同倒置的浮桥[4]。锚索式悬浮隧道的管体通过柔性锚索与海床固定,类似安放中的沉管[5-6]。对后者的研究发展了众多锚索布置方案,包括两斜缆[7]、两竖缆[8-9]、两斜两竖缆[8-9]、一斜两竖缆[9]、两撇两捺四斜缆[7-9]、以及倒置索桥[10]等。此外还有竖缆与斜缆纵向混搭布置[11]以及锚索与浮筒组合方案[1,9]。本文设置1 km长直线形悬浮隧道模型,设置7种特征锚索布置,并进行定量结构分析与综合评价。
1 方法
1.1 计算模型、参数与假设
拟定6个锚索布置方案,见图1。所有方案隧道管体总长均为1 km,锚索垂向投影长度均为100 m。方案A~D锚索均与管体轴线垂直,每个锚固断面横向特征可描述为“两竖两斜”、“两撇两捺”、“一撇一捺”和“两竖”,后者似张力腿。方案E~F锚索为空间布置。方案E~F的正视图参考方案C。方案A~E锚固断面纵向间距及相应锚点的纵向间距均为100 m,而F的分别为50 m和500 m。

图1 锚索布置方案(m)Fig.1 Mooring layout options(m)
所有方案锚索参数均假设为一种材质和型号:直径0.08 m,有效面积0.005 03 m2,弹性模量210×109Pa,线质量密度 39.458 kg/m,泊松比0.3。假设缆索初始伸长量足够大,荷载作用下也不松弛。忽略锚索垂度效应,也即锚索对管体的约束刚度均由其自身伸缩弹性提供。
假设管体两端完全固结,管体横断面为圆管,外径10 m,内径8 m,且该尺寸沿隧道管体纵向不变,弹性模量36×109Pa、泊松比0.2,材料密度2 550 kg/m3,结构系统阻尼与水阻尼合计按计算阻尼比0.05考虑。
假设管体两端完全固结,锚点基础完全固定。
1.2 计算工况
本文提出用于悬浮隧道方案综合比选的锚索布置评价指标。
1)缆索工程量,包括长度与根数,前者主要影响水上施工设备,后者主要影响水上作业次数;
2)管体在水平或竖向均布静载作用下的响应,即挠度、转角、最大缆力和最大基础反力。水平与竖向荷载取值均为138 kN/m,该荷载可使管体跨中产生约2 m挠度;
3)管体在均布扭矩作用下扭角。扭矩荷载取值为600 kN·m/m,该荷载可使管体跨中产生约0.5°扭角;
4)管体水平基频、竖向基频和扭转基频;
5)管体跨中施加1 m强制位移再释放,通过自由衰减过程观察能耗规律。
1.3 计算方法
采用ANSYS-APDL命令流建模和分析,管体采用beam188梁单元,划分精度5 m。为考虑管体的扭转效应,在管体中心处建立与直径等长刚臂,缆索与管体通过刚臂连接,刚臂采用beam188梁单元建模,刚度设置接近无穷大。缆索采用link8杆单元建模。结构阻尼和水阻尼均采用瑞利阻尼施加。
静力荷载分析考虑几何非线性采用Newton-Raphson法。基频计算采用模态分析。能耗分析采用完全瞬态分析。
2 结果与分析
2.1 工程量与安装次数
图2总结了每个方案所需缆索总长度和总根数。方案F工程量最大,方案D工程量最小。值得一提的是,同等水深条件下方案D单根锚索长度最短为100 m,方案F锚索长度最长为256 m。

图2 缆索工程量统计Fig.2 Quantity of cables
2.2 管体响应
图3 是各锚索布置方案水平和竖向均布荷载作用下悬浮隧道管体挠度沿其长度分布值。可见:
1)水平和竖向最大挠度方案C和D、F出现在跨中,其它方案中间1/3~2/3段挠度相等;说明前者跨中位移仍受岸边约束影响,而后者跨中位移基本只受沿程锚固影响;

图3 各锚索布置方案静力均布荷载作用下沿程挠度Fig.3 Deflection along tube length under uniform loading of each mooring options
2)方案D水平挠度最大,方案B水平挠度最小;
3)方案F竖向挠度最大,方案A竖向挠度最小。
图4(a)为各锚固方案水平均布荷载作用下跨中转角,也即最大转角,可见方案A、C、E、F管体发生水平位移时锚索产生水平约束分力的同时也产生了扭矩,方案B产生约束分力却避免扭矩的产生(证明了文献[8]结论),而方案D只有竖缆索所以几乎无水平向约束分力,也不产生扭矩。
图4(b)为各锚固方案扭转均布荷载作用下跨中转角。可见方案跨中扭角几乎一样。也即所有方案抵抗扭转能力相同,这意味着尽管本算例隧道长1 000 m,管径10 m,也即长高比达到100∶1,管体抗扭绝大部分贡献仍来自其端部约束,前提是岸边接头对管体扭转为完全固结约束。

图4 各锚索布置方案均布荷载作用下跨中转角值Fig.4 Twisting anglein mid-section under uniform loading of each mooring options
综上,各锚索布置方案引起扭转能力差异大,抵抗扭转能力均可被忽略。
2.3 缆力与锚点力极值及位置分布
考察悬浮隧道均布静力荷载作用下最大缆力与最大锚点力及位置分布。
表1为竖向均布荷载作用下响应汇总表。可见:1)方案B、C、E最大缆力均发生在隧道正中锚固断面的斜缆上,而方案A最大缆力发生在邻近正中锚固断面的竖缆上;2)方案C缆力最大也最不均匀(也即缆力分布标准差最大),方案A缆力最小,方案B缆力最均匀;上述可见缆力在纵向上的不均大于横向的;3)方案F锚点力最大,方案B锚点力最小。

表1 各方案竖向均布荷载下最大缆力与锚点力Table 1 Maximum cable force and anchoring force of mooring optionsunder distributed vertical load kN
表2为水平向均布荷载作用下响应汇总表。可见:1)方案A~D最大缆力均发生在隧道正中锚固断面背流侧的斜缆上(注:前文已述缆力有足够大初张力,因此背流侧锚索通过收缩释放缆力来约束管体位移,也即本文所述“缆力”可理解为“缆力变化”)。方案E最大缆力发生在靠近中心处。2)方案C缆力最大且最不均,方案D缆力最小且分布最均匀;3)方案F锚点力最大,而方案D锚点力最小。

表2 各方案水平均布荷载下最大缆力与锚点力Table 2 Maximum cable and anchoring forcesof mooring optionsunder distributed horizontal load kN
2.4 自振与能耗特性

图5 典型锚固方案悬浮隧道结构模态分析一阶振型形态Fig.5 First vibration modal shape of submerged floating tunnel structure with typical mooring options

图6 各锚固方案相对基频Fig.6 Relative frequency of mooring options
对各锚索布置方案进行模态分析(图5为部分方案的第一振型位移形态),得到各自水平、竖向和扭转的自振基频。并且同样方法可求出去掉沿程锚索自由式悬浮隧道结构的水平、竖向和扭转基频,分别为0.04 Hz、0.04 Hz和1.21 Hz;将带有锚索布置的结果除以自由式的结果,见图6。可知,水平向基频最大的是方案B和E,而竖向基频最大的是方案A。各方案扭转基频基本相等,该规律与图4(b)一致。

图7 典型方案管体跨中位移时历衰减过程Fig.7 Typical optionsmid-point displacement-time decay process
2.5 多方案等工程量比较
上文分析比较的假定是所有锚索布置方案的锚索同材质、同面积。下面考虑所有方案同锚索工程量比较,也即所有方案的锚索长度乘以面积均相等。表3将方案C设置成基准方案,其它方案响应计算结果根据与方案C的工程量比值来进行换算。举例说明:根据图2(a),方案A与方案C工程量换算系数为4 346/2 546=1.707,则A响应计算结果中的挠度、缆力、锚力均乘以该系数,而频率除以该系数。其它方案同样处置。由表3换算结果可见,方案A、B总体性价比较高;当不需控制管体水平位移时,方案D性价比最高。
自振衰减结果见图7。当模型运动位移低于0.000 4 m时记录自振持续时间。发现方案A所需时间最短,自由衰减开始到静止的时间仅需要42 s,而方案F最长需要150 s。可见,对于本文算法而言耗能快慢主要由体系刚度控制,而非锚索质量,真实情况需通过物模试验更深入研究。
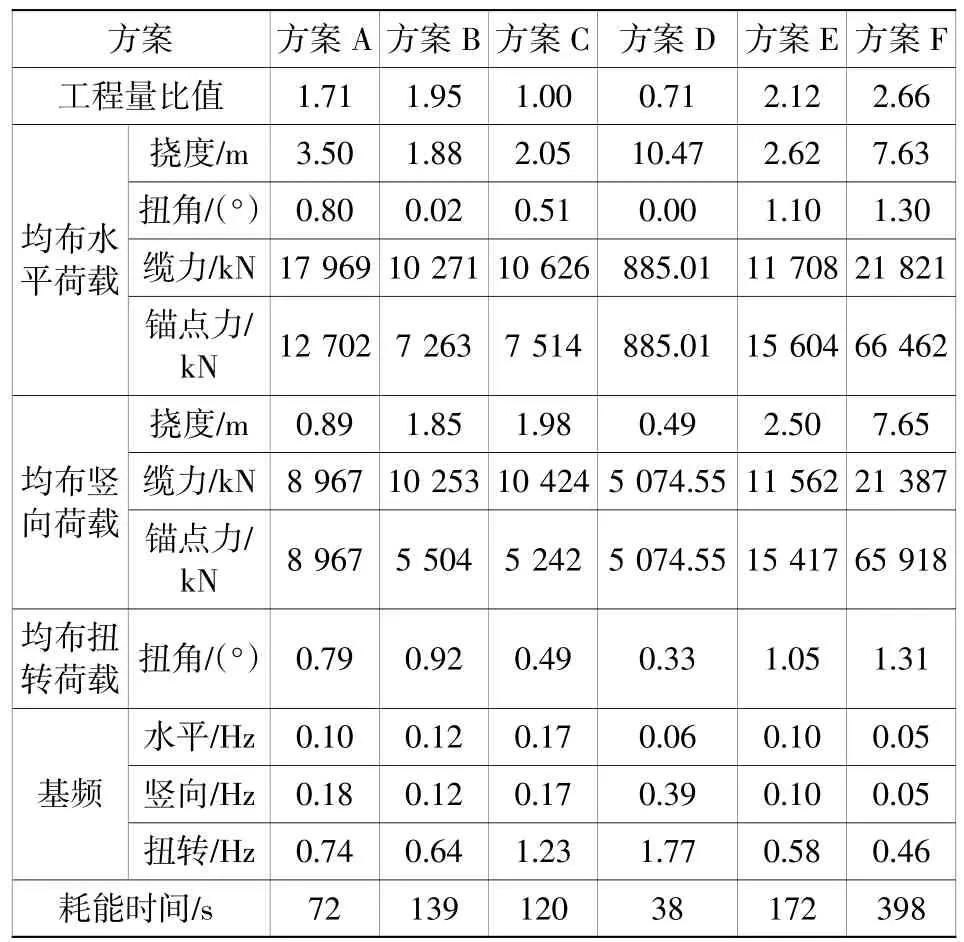
表3 等工程量各锚索布置方案响应换算结果Table3 Response conversion resultsof equivalent cable-quantity-mooring options
3 结语
1)空间缆索布置方案的缆索用量较大,约为横向缆索布置方案的1.1~1.3倍;2)“两竖”方案不约束管体平面位移,因而也不引起管体扭转;“两斜两竖”或“两斜”等方案约束管体平面位移的同时,引起管体扭转;“两撇两捺”方案既约束平面位移又不引起额外扭转;3)管体跨中区间沿程挠度有可能受制于沿程约束和端部约束,也有可能只受制于沿程约束;4)当管体端部完全固结时,其扭转刚度贡献主要由自身结构扭转刚度提供,沿程锚索系统刚度的贡献相比很小可忽略;5)缆力最大的方案通常也是缆力分布最不均的方案;6)锚索与管体垂直布设方案性价比普遍较高。

