悬浮隧道施工过程结构特征参数与设计关键参数研究

魏佳奇 ，林巍 ，杨自豪 ，张洁琼 ，邹威

（1.中交悬浮隧道结构与设计方法研究攻关组，广东 珠海 519000；2.西北工业大学数学与统计学院，陕西 西安 710072；3.大连理工大学，辽宁 大连 116024；4.中交公路规划设计院有限公司，北京 100088）

0 引言

悬浮隧道施工时的特点通常是其管体一端被约束，一端无约束，后者也可称为“自由”。管体总长度随施工进度而加长。悬浮隧道安装工艺有分段顶推法和水下连接法[1]；其最可能的安装顺序是从一端往另一端拼装或顶推，逐渐增长。对于较短的悬浮隧道或水动力较弱的施工环境，在拖轮等设备条件允许时，也可考虑一次安装（一次安装本文不再赘述）。当管体有锚固系统时，锚固系统也对管体起到约束作用。悬浮隧道锚固系统的形式有浮筒或锚索或两者组合。悬浮隧道完工后，或在更遥远的运营时期，其管体长度不再改变，且管体两端与岸边连接，连接方式可以被设计成刚性的固结[2]，柔性的铰接[3]，或介于其中的某种方式。本文仅比较前2种的“极端”形式对悬浮隧道施工时期结构体系的影响以及与完工后结构体系的比较。

本文通过设定管体与锚固系统的刚度贡献综合比较参数Õ；观察不同Õ取值时，悬浮隧道每个施工步数管体长度不同状态时第一阶自振周期、自由端挠度、约束端剪力和弯矩，为观察方便和指导设计分析，将这些值与隧道完工后同类值相除，即无量纲化，研究该值的变化规律以及与Õ的对应关系。

1 研究方法

设定悬浮隧道评价参数Õ；找出真实工程悬浮隧道结构可能参数范围；比选、确认并建立计算模型和假定，综合考虑大量计算工作、横向比较目的及计算出错风险，选择简单直观的计算模型和方法；将施工期的结构特征参数结果与运营期的相除（无量纲化），选取不同Õ值，进行横向比较与观察，并研究铰接和固结方式对悬浮隧道施工期的影响和规律。

1.1 悬浮隧道评价参数

悬浮隧道纵向结构计算参数涉及隧道（管体）长度L、横断面（弹性阶段）抗弯参数EI、隧道延米质量m和锚固系统对隧道在水平向或竖向提供刚度的沿着隧道管体纵向每米的等效值（又称“弹性地基梁刚度系数”）k。可见悬浮隧道参数组合之多，研究工作千头万绪，为了把握这4个参数的内在规律，在Sato系数的基础上[4]，进一步提出施工关键工况特征参数Õ，将Õ=1定义为该隧道两端固结时受到水平或竖向均布荷载时所产生的跨中挠度，与两端无约束时受到同样荷载所产生的跨中挠度相等。也即：

经试算发现，只要保证Õ数值不变，改变悬浮隧道的公式Õ中的其它结构特征参数，后述第1.4节中无量纲的研究对象的值不会发生改变，有量纲的研究对象之间的相对比例以及随着施工步骤管节长度变化曲线的特征也不会改变。

1.2 参数取值范围

考虑工程范围实际参数，管体和锚固系统结构参数取值假定：50≤L≤5 000；9×1012≤EI≤1.7×1015；50≤m≤5 000；0≤k≤1.3×106。其中：L为管体长度，m；m为悬浮隧道管体每延米质量，kg/m，假定附加水质量2倍效应；k为锚固系统垂直于隧道管体长度方向每延米平均刚度在水平向以及竖向的包络范围，N/m/m；EI为横断面抗弯刚度指标，N·m2；I为惯性矩；E为截面构造综合弹性模量。

EI及m取值范围来自图1中3个不同尺度和特征悬浮隧道横断面，图1（a）为内径4 m、外径5 m的圆管；图1（b）为宽30 m、高9 m的箱形；图1（c）为总宽52.6 m、高为12.6 m的分离式双圆管横断面。

图1 横断面参数取值参考图Fig.1 Cross-sections parameter reference sketch

1.3 计算模型假设、方法比选与局限性

悬浮隧道纵向结构需考虑的因素包括自振频率、挠度、约束端弯矩和剪力。从设计计算简化且不易出错的角度考虑，将悬浮隧道分为水平向和竖向2个2D平面问题。忽略锚固体系自身质量（也即忽略锚索的质量或忽略浮筒和竖向连接管的质量），进而锚固系统对悬浮隧道提供的水平或竖向刚度可进一步简化为弹簧。利用商业软件ANAYS建模、基于Matlab的二维结构编程，以及理论解编程3种方式进行横向比较与比选，从计算量以及分析结果风险角度考虑，本文选择了方便快捷的理论解作为本文的主要研究方法，其余两者作为验证比较手段。

假设1.2节参数均为常数，并假设锚固系统沿着管体长度方向的约束作用是连续的，可列出微分方程。结合4种不同边界条件：两端固结、两端铰接、一端固结和一端自由、一端铰接和一端自由，可求出方程沿着隧道长度里程的挠度精确解。精确解与数值解结果比较相符。挠度方程沿着隧道长度方向求2次和3次导数就得到管体的弯矩和剪力方程。

本文的研究方法是横向比较施工全过程与施工后（运营期）悬浮隧道的结构特征参数或响应，以及横向比较固结和铰接两种约束方式对于悬浮隧道施工全过程受力和自振周期的特点与优缺点，因此理想化的、有精确解的计算模型能达到本文目的，而对于悬浮隧道结构自身响应的研究，则应发展更真实的模型计算。

1.4 研究成果策划

为了上述横向比较目的，研究悬浮隧道施工阶段和完工后在相同均布荷载下的挠度和内力，前者对应施工悬浮隧道的管体自由端和完工悬浮隧道的跨中，后者对应施工及完工悬浮隧道约束端的剪力和弯矩。将施工时的内力或挠度分别除以完工后的内力或挠度，得到的数值如果小于1，代表施工期的悬浮隧道相对运营期同等荷载条件下偏安全，反之亦然。并研究结构体系主要自振周期。研究内容总述见表1。

表1 研究内容总述Table 1 Summary of research contents

2 结果与分析

2.1 结构响应分析

分析得到相对挠度、一阶自振周期、相对自振周期、约束端剪力、相对剪力以及相对弯矩随施工长度的改变，典型计算结果见图2～图8。

图2、图3为Õ=0.4时，不同接岸接头方式下相对挠度随施工长度的变化。可见施工过程悬浮隧道变形姿态特征始终在改变。当约束端采用固结或铰接时，悬浮隧道在施工期的最大挠度与运营期最大挠度的比值均随着施工长度的增大而不断增大；当施工长度大于1 000 m时，采用固结方式时该比值趋于稳定，采用铰接方式时该比值有下降的趋势。

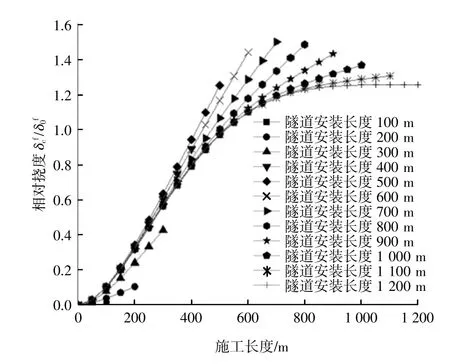
图2 一端固结一端自由时相对挠度随施工长度的变化Fig.2 Relative deflection varieswith construction length when one end is consolidated and oneend isfree

图3 一端铰接一端自由时相对挠度随施工长度的变化Fig.3 Relative deflection changeswith construction length when one end is hinged and one end isfree

图4 为采用不同接岸接头方式下，一阶自振周期随施工长度的变化。尽管铰接对悬浮隧道管体的约束弱于固结，但是由于其锚固体系支撑特征，铰接的自振周期反而更短一些；在施工全过程中一端固结的悬浮隧道的自振频率大约是一端铰接时的1～3倍；一端铰接的悬浮隧道全过程施工时自振周期随着管体长度几乎呈线性的增长；当Õ＜0.5时，一端固结的悬浮隧道完成一半管体的水下安装后自振周期趋于稳定。相对自振周期变化见图5。

图5可见，无论采用铰接还是固结的接岸接头方式，当Õ小于1时，相对自振周期均随着施工长度的增长先增大后趋于稳定；随着Õ的增大，相对自振周期均随着施工长度的增大而增大（不收敛）。

图4 一阶自振周期随施工长度的变化Fig.4 Variation of first-order natural vibration period with construction length

图5 不同Õ时相对自振周期随施工长度的改变Fig.5 Changeof relative natural vibration period with construction length under differentÕconditions

图6 为不同接岸接头方式下，约束端剪力随施工长度的变化。由图6可分析出，对于悬浮隧道任意结构，当接岸接头采用固结形式时施工时期约束端剪力大约为铰接形式的2～4倍；接岸接头采用固结形式时，当Õ＜4，隧道长度建设了一半或更短时端部剪力就不再发生改变（收敛至恒定值），反之则约束段管体剪力随着隧道长度一直增加（不收敛）；接岸接头采用铰接形式，当Õ＜0.5，隧道长度建设了一半或更短时端部剪力就不再发生改变（收敛至恒定值），反之则约束段管体剪力随着隧道长度一直增加（不收敛）。

图7为当Õ=0.4时，不同接岸接头方式下相对剪力随施工长度的变化。两种约束方式下的曲线均先增大后趋于稳定，当施工长度小于600 m时，固结比铰接的相对弯矩大，反之则相反。

图6 约束端剪力随施工长度的变化Fig.6 Changeof shear force at constraint end with construction length

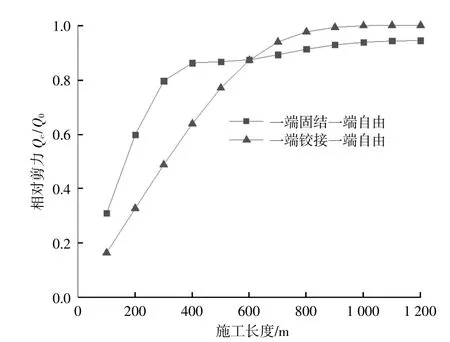
图7 相对剪力随施工长度的改变Fig.7 Relative shear force changeswith construction length

图8 为一端固结一端自由时，不同Õ取值情况下约束端弯矩与施工完成时同位置弯矩的比值随施工长度的变化。可以观察到在相同的施工长度下，相对弯矩随着Õ的增大而增大；不同Õ时，相对弯矩均随施工长度的增长先增大后趋于稳定，且随着Õ的增大，趋于稳定时的施工长度随之增大（即拐点后移）。

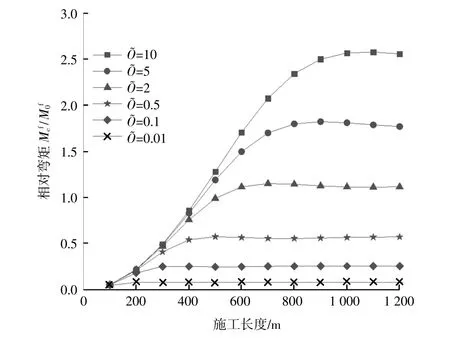
图8 相对弯矩随管体施工长度的改变Fig.8 Relativebending moment changeswith tube length

2.2 参数Õ对悬浮隧道施工期结构自振与响应特征的界定与指导

悬浮隧道在施工期随着其长度增加在均布荷载作用下的挠度变化、内力变化和自振周期的变化，相比其完工后或运营期的同等条件下的挠度、内力或自振周期的特征以及相对应的Õ的取值，见表2。

表2 参数Õ对悬浮隧道施工期结构自振与响应特征的界定Table 2 Classification of structural self-vibration and response characteristics during SFT construction to parameterÕ

由表 2可见：1）当Õ≤0.4或1时，约束端采用固结或铰接时的悬浮隧道在施工期的最大挠度和运营期接近，前者不超过后者的1.5倍，施工期相对不控制隧道的结构设计；其它情况时则需注意验算悬浮隧道整个施工期不同长度时的挠度，即施工期需要注意控制挠度；2）当约束端为固结时，悬浮隧道结构参数0＜Õ≤44时，其管体端部最大剪力不超过运营期同等均布荷载条件下的1.5倍，考虑施工期荷载条件比运营期较有利，这时施工期荷载条件可能不作为结构设计方案的控制因素；反之，当Õ＞44时，需要注意验算施工期管体约束端的剪力；3）当约束端为铰接时，任意悬浮隧道结构形式施工全过程的端部剪力均小于施工完成后剪力的1.5倍，较安全；4）当悬浮隧道施工时约束端为固结时，其管体的弯矩特点类似1）的特点，需要根据不同的Õ值分情况讨论；5）有关悬浮隧道施工期的固有周期和其运营期的固有周期的关联，当约束方式为固结和铰接分别对应0＜Õ≤0.3和0＜Õ≤2.5时，结构施工时期不同长度的固有自振周期与运营期的固有自振周期相近，范围在±20%之内，如果运营期的结构设置合理，施工期也较不易发生共振的风险；反之则需注意施工阶段悬浮隧道结构的共振问题。

3 结语

本文将悬浮隧道简化为弹性地基梁，利用理论解公式，分析了在不同工况下施工期间结构挠度、内力以及一阶自振周期的变化。主要研究结论如下：

1）尽管悬浮隧道在施工期暴露在不利工况下的概率较低，经受的各种荷载（如水流）相对运营期偏小，但本文计算结果表明施工时悬浮隧道结构安全有可能成为结构设计的控制工况。

2）本文通过简化模型方程找到基于理论解发展的一种快速判断悬浮隧道施工过程相对安全性的计算方法。

3）施工期间，结构挠度、内力及频率与管体刚度EI、锚固系统刚度k及约束方式关联较大。

4）当参数Õ相同情况下，采用铰接时约束端剪力以及结构一阶自振周期比采用固结时小。

5）悬浮隧道设计时可通过计算Õ值并对应查表2，加深对悬浮隧道施工期结构力学特征的认识。