悬浮隧道纵向结构受力工程规律研究
刘凌锋 ,刘晓东 ,林巍 ,刘傲祥 ,魏佳奇 ,3
(1.中交悬浮隧道结构与设计方法研究攻关组,广东 珠海 519000;2.中交公路规划设计院有限公司,北京 100088;3.大连理工大学,辽宁 大连 116024)
0 引言
悬浮隧道是悬浮于水面以下一定深度的管状结构,主要构成部分包括隧道管段、接头与锚固系统等[1],其纵向结构则主要关心其线形、锚索布置等问题[2]。本文基于中交悬浮隧道结构设计与方法研究攻关组工作内容,对包括水平线形、管节刚度、接头刚度、缆索刚度、基础沉降以及缆索失效等悬浮隧道纵向结构相关工程参数开展研究,并对部分参数进行敏感性分析。
1 总述
本文分析采用有限元软件ANSYS,并作如下假设:1)管体横断面沿纵向不变;2)两端接岸接头完全固结;3)不考虑中间接头刚度变化,管节两端固结;4)忽略锚索垂度;5)锚索不发生松弛;6)不考虑基础与缆索耦合作用。
如无特殊说明,各章节研究算例及参数如表1所示。

表1 方法总述表Table 1 Summary of methods
2 水平线形
将平曲线形悬浮隧道响应结果除以直线的,得图1。可见随着平曲率半径增大,管体扭矩减小(直线形悬浮隧道扭矩几乎为0),水平弯矩及挠度总体呈线性增大并逐渐趋向于直线形悬浮隧道。
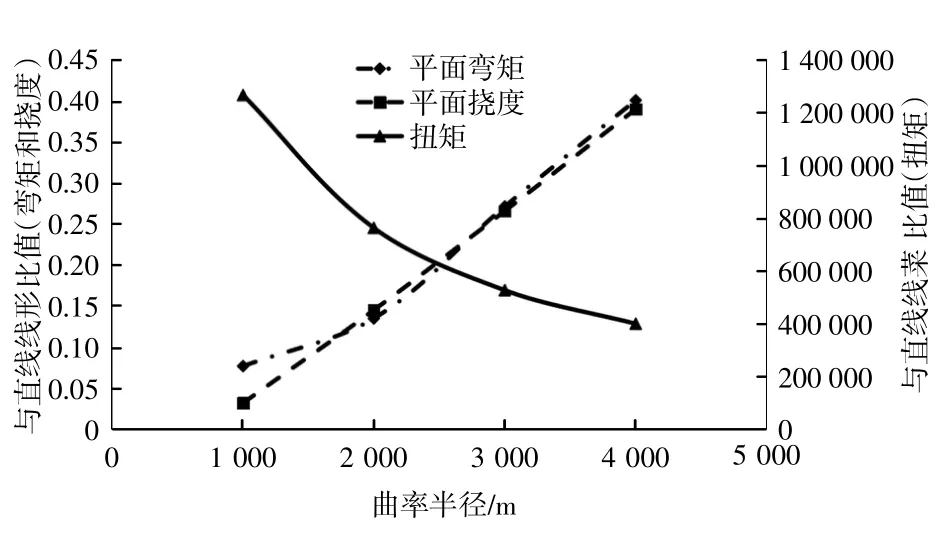
图1 均布荷载作用下不同水平线形隧道管体的响应Fig.1 Tunnel tube responseof different planealignment under uniform loading
显然,从抵抗水平荷载作用效应来看,圆曲线形比直线形悬浮隧道更优,且曲率半径越小,抵抗水流作用能力越强,管体所受水平弯矩也越小。但同时由于曲率半径减小时,管体所受扭矩增大,所以圆曲线形悬浮隧道的曲率半径应在管体挠度、弯矩和扭转的考量中取折中值。结合JTG D20—2017《公路路线设计规范》[3],当车速为120 km/h时,圆曲线最小半径取1 000 m。因此对于本算例,曲率半径在1 000 m以上且挠度和弯矩不超过承载力及规范要求时较好。
3 管节刚度
悬浮隧道结构设计时,管体不同抗弯刚度EI对悬浮隧道体系受力和变形影响较大。通过改变弹性模量E,将EI增大为其初始值的2~4倍,研究同等水平和竖向均布静力荷载作用下结构响应变化(见图2)。发现:随着管体弹模增大,管体挠度及缆索缆力线性减小,管体弯矩和剪力增大,且弯矩增加速率大于剪力增加的速率。原因易理解:管节刚度增大,隧道变刚,故挠度减小,而增大刚度的管体分担更多荷载,缆索分担荷载相应减小,故管体内力增大,缆索缆力变小。

图2 不同弹模时管体挠度和内力变化趋势图Fig.2 Variation trend of tube deflection and internal force under different elastic modulus
4 接头刚度
4.1 中间接头刚度
悬浮隧道可能有中间接头。通过在接头部位设置3个平动、3个转动共6自由度对应的6个弹簧模拟特殊接头刚度。将管体轴向刚度EA、抗弯刚度EI作为基准刚度,中间接头6个自由度的约束的弹簧刚度分别取为以上的0.001、0.005、0.01、0.05、0.2、0.4、0.6、0.8、1、2 及 10 倍。发现:随着中间接头刚度增大,管体挠度减小,内力增大,且水平响应比竖向更敏感。图3为管体挠度随中间接头刚度变化的曲线,当中间接头刚度达到基准刚度0.2倍左右时,管体挠度和内力趋于稳定。该发现在接头刚度设计取值时值得考虑。

图3 管体挠度随中间接头刚度变化规律Fig.3 Variation of tube deflection with stiffnessof segmental joint
4.2 接岸接头刚度
悬浮隧道接岸接头是管体与岸边的接头,通过假设不同的接头刚度组合,研究发现规律与中间接头相同。
5 缆索刚度
5.1 刚度整体升降
拉锚式悬浮隧道设计时,改变缆索的弹性模量、截面面积、锚固间距或缆索夹角,将引起锚固系统整体刚度的变化。为研究锚固系统刚度整体升降如何影响悬浮隧道体系的受力状态,固定其他参数不变,进行如下单因素变化分析:
1)假定缆索间距从50 m、100 m、150 m、200 m发生变化,在净浮力和水流力作用下,研究隧道体系的响应变化;
基于以上种种情况,高职院校培养的毕业生中,有不少人学业不精、业务不熟、做事浮躁。而用人单位所急需的是来则能战、战则能胜,专业知识熟记于心、业务娴熟干练、沟通能力强的财务人员。高职院校培养的毕业生依然走不出“三三制”的怪圈:三分之一毕业即失业、三分之一能找到工作、三分之一能找到会计工作(即使找到会计工作的,也大多数是最基础的收银员、出纳员之类)。据有关数据显示,目前我国持有会计从业资格证书人数约1600万人,其中,正在从事或曾经从事会计工作的约72%,没有从事会计工作的约占28%。
2)固定其他参数不变,假定斜缆与竖直线夹角 α 从 15°、30°、45°、60°发生变化,在净浮力和水流力作用下,研究隧道体系的响应变化。
结果见表2。

表2 缆索间距和夹角变化对结构响应影响的敏感系数表Table2 Sensitivity coefficient of cable spacing and cable angle changes to structureresponse
可见:1)缆索间距增大,隧道管体挠度、弯矩、剪力以及缆力均增大。原因在于在缆索间距变大,则锚固系统刚度降低,对管体的支持力度变小,因此结构体系的内力及挠度增大。此规律与第3节管节刚度研究结论吻合,锚固系统刚度与管节刚度存在此消彼长的关系;2)缆索夹角增大,隧道管体水平响应减小,竖向响应变大。原因在于缆索夹角增大时,锚固系统水平刚度增大,竖向刚度减小;3)对于本算例,缆索间距改变比其夹角改变对结构响应影响更大。
5.2 局部刚度降低
分析当隧道端部、1/4隧道长度位置以及隧道跨中分别发生单个锚固断面缆索刚度降低0%(原刚度)、降低10%、50%和100%(即完全失效)时,共12个工况下隧道体系的响应。获得隧道挠度及内力、缆索拉力对缆索局部刚度降低的敏感系数,刚度降低50%时的敏感系数见表3。
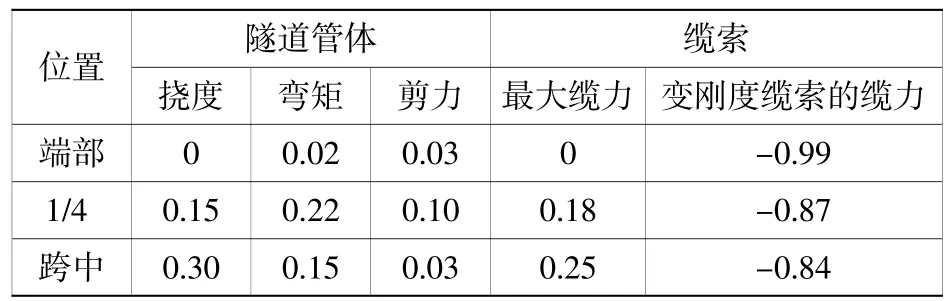
表3 缆索局部刚度降低敏感系数表Table 3 Sensitivity coefficient of local cable stiffness reduction
发现:1)缆索局部刚度降低,隧道管体挠度、内力以及最大缆力均增大;2)管体挠度和最大缆力在跨中位置变化最敏感;管体内力在1/4长度位置最敏感;3)任意位置的缆索刚度改变时,该缆索的缆力将发生剧烈变化。
5.3 斜缆与竖缆刚度分配
为探索斜缆与竖缆的刚度分配对悬浮隧道结构体系静动力响应的影响,建立拉锚式悬浮隧道有限元模型,控制竖缆刚度值,让斜缆刚度从0倍、0.2倍、0.4倍……1倍、2倍、4倍……10倍、1 000倍竖缆刚度进行变化,分别计算结构在相同水流力作用下的内力及变形,发现:
1)斜缆刚度/竖缆刚度=0时,隧道跨中转角为0(小变形计算前提);
2)随着斜缆刚度/竖缆刚度增大,管体最大弯矩、剪力均减小(图4),对接岸接头结构设计有利。但与此同时,隧道跨中转角增大;
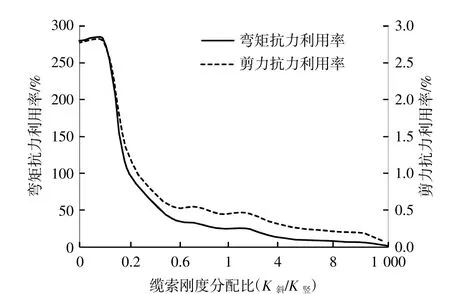
图4 横断面抗力利用率Fig.4 Cross-section resistance utilization rate
3)当斜缆刚度/竖缆刚度>4时,隧道端部弯矩、剪力及跨中转角均收敛。
上述发现可供拉锚式悬浮隧道缆索刚度分配比设计时参考。
5.4 海底形状
海底形状起伏将导致缆索长度变化,从而使缆索刚度产生变化。为探究海底形状影响,对悬浮隧道锚在特征海床形状与理想平底海床时进行典型动静力工况计算并比较响应结果,均布水流力作用下特征海床形状与理想平底海床计算结果见表4。
可见,地形变化对结果影响大。本算例中,特征海底形状的管体内力偏小32%,原因是隧道两端缆索长度短,刚度增大。作者通过改变海床凸凹进行其它计算计较。综上结论是,工程计算不应忽略海床面实际凸凹不平。
6 基础不均匀沉降
对于自由式悬浮隧道,不存在锚固系统沉降的问题(因为没有锚固系统);对于浮筒式悬浮隧道,其锚固系统可能随着水位变化而产生起伏,但可以通过浮筒内压载水量的变化进行调整;对于拉锚式悬浮隧道,其缆索与海底的锚固基础在运营期间可能出现不均匀沉降的问题。
考虑3种全断面缆索基础沉降类型共9种沉降工况(图5):1)4处缆索沉降:海中段3~6号缆索同时发生基础沉降;2)2处缆索沉降:3/6、4/5、3/5、3/4号缆索基础沉降;3)单处缆索沉降:1、2、3、4号缆索分别发生基础沉降。

图5 计算示意图Fig.5 Calculation schematic diagram
考虑4种同个锚固断面缆索的不均匀沉降:1)单根竖缆沉降;2)单根斜缆沉降;3)2根竖缆沉降;4)1斜1竖沉降。并认为悬浮隧道管体结构可以承受这些沉降工况,仅比较不同沉降类型和沉降位置引起的管体及缆索内力大小。
将不发生锚固基础沉降的工况定义为基准工况,计算得到所有沉降工况下的管体及缆索内力后,分别除以基准工况的相应内力值,从而将各内力无量纲化,如图6所示。

图6 基础不均匀沉降工况计算结果Fig.6 Calculation resultsof uneven foundation settlement conditions
可见:1)沉降工况引起管体响应及缆索内力的增大;2)全断面缆索基础沉降组合中,4处缆索沉降工况引起的响应最小,单处缆索沉降引起的响应最大,且靠近隧道端部的缆索沉降比跨中缆索沉降更为不利,1号近岸缆索基础沉降工况为所有沉降工况中的最不利工况;3)单根斜缆沉降引起的内力增量最小,2根竖缆沉降工况与1斜1竖沉降工况对管体及缆索内力影响近乎相同。
7 缆索失效分析
考虑图5(a)中的1断面、2断面、3断面或4断面发生缆索全断面失效。计算获得各工况隧道管体挠度及内力,并用与第3节同样的方法将各工况内力无量纲化,见图7。

图7 全断面缆索失效工况内力计算结果图Fig.7 Internal force calculation result of full section cable under failure condition
发现:1)缆索失效位置越靠近隧道跨中,则缆索失效引起的管体挠度越大;2)对于本算例,缆索最大拉力与缆索失效位置没有明显关系,缆索失效对缆力影响不大;3)从隧道管体最大弯矩和最大剪力来看,2断面缆索失效为最不利工况。
以横断面2斜2竖缆索布置形式为例,分析同个锚固断面中2种单根缆索失效工况:1)单根竖缆失效;2)单根斜缆失效。计算结果与基准工况比值见图8。

图8 单根缆索失效工况计算结果图Fig.8 Calculation results of single cable failure condition
可见:1)单根缆索失效对管体内力影响不大,对缆索拉力及管体挠度影响较大;2)单根竖缆失效比单根斜缆失效影响大。
8 结语
本文主要发现:1)悬浮隧道水平曲率半径应综合考虑管体挠度、弯矩和扭转并结合规范进行取值;2)管节刚度与缆索刚度对隧道体系的影响此消彼长,接头刚度变化与管节刚度变化影响规律类似;3)近岸缆索沉降或单根竖缆沉降是较不利的;4)跨中缆索失效引起管体挠度增量较大。

