对一道质量检测试题的探究
福建省宁德市高级中学
题目(2018年合肥高三第二次质检第20题) 已知点A(1,0)和动点B,以线段AB为直径的圆内切于圆
(1) 求动点B的轨迹方程;
(2) 已知点P(2,0),Q(2,-1),经过点Q的直线l与动点B的轨迹交于M,N两点,求证:直线PM,PN的斜率之和为定值.
本题的答案是:(1) 动点B的轨迹方程为:(2) 直线PM,PN的斜率之和为定值3.
对于本题(2),至目前笔者尚未发现有相关的探究文章.教学中,如果就题论题,解完即止,那就失去了一个很好的发现、探究的机会.我们可以引导学生对之进行分析,适当挖掘,提出有价值的问题进行探究,导出有意义的结论,从中培养和提升学生的探究能力、创新能力和数学素养.
1.特殊引路猜测结论
不难发现,本题(2)的定值3 取决于定点P(2,0)和Q(2,-1),其中点P(2,0) 为椭圆的右顶点,点Q(2,-1) 为过椭圆的右顶点P(2,0)且垂直于x轴的直线x=2 上的一个定点.本题(2)的结论表明:经过定点Q(2,-1)的直线l与椭圆M,N两点,P为椭圆的右顶点,则直线PM,PN的斜率之和为定值3.的右顶点P与过定点Q(2,-1)的直线l的内在联系,若把过椭圆右顶点P且垂直于x轴的直线x=2 上的特殊定点Q(2,-1) 换为直线x=2 上的任一个定点Q(2,n)(0),那么,直线PM,PN的斜率之和是否仍为某个定值?
探究1先以定点Q(2,1) 试验.设直线l的方程为y=k(x-2)+1,代入得3x2+4(kx-2k+1)2-12=0,整理得(4k2+3)x2-8k(2k-1)x+4(2k-1)2-12=0.设M(x1,y1),N(x2,y2).据韦达定理,得

又设直线PM,PN的斜率分别为k1,k2,则
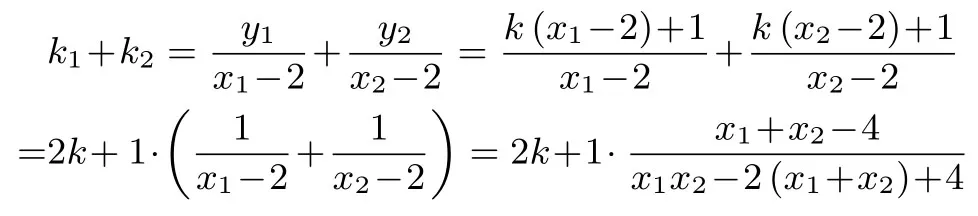

即直线PM,PN的斜率之和为定值-3.由于定值由此猜测:对于直线x=2 上的任一个定点Q(2,n)(0),直线PM,PN的斜率之和为定值
经探究,此猜测成立.其证明如下:
证明当直线l垂直于x轴时,直线l的方程为x=2.显然,直线l与椭圆相切,不合题意,故直线l不垂直于x轴.设直线l的方程为y=k(x-2)+n,以n代替上述探究中的“1”,可得进而可得

即直线PM,PN的斜率之和为定值可见,猜测成立.特别地,当n=-1时,直线PM,PN的斜率之和为定值3.这就是上述试题(2)的答案.
2.探究一般性结论
问题2由于椭圆的b2=3,故上述结论表明:对于椭圆右顶点P(2,0) 及定点Q(2,n)(0),直线PM,PN的斜率之和为定值那么,对于一般的椭圆右顶点P(a,0) 及定点Q(a,n)(0),直线PM,PN的斜率之和是否为定值
探究2经探究,对于一般的椭圆及其右顶点P(a,0),直线l过定点Q(a,n)(0) 时,直线PM,PN的斜率之和为定值反之也真,且对左顶点P(-a,0) 也有相应的结论.
结论1已知P为椭圆的右或左顶点,常
问题1上述结论揭示了椭圆数0,不经过点P的直线l与椭圆交于M,N两点,则
(1) 对于右顶点P(a,0),直线PM,PN的斜率之和为定值的充要条件是直线l过定点Q(a,n);
(2) 对于左顶点P(-a,0) 直线PM,PN的斜率之和为定值的充要条件是直线l过定点Q(-a,n).
证明先证明(1).充分性:若直线l过定点Q(a,n)(0),由直线l不经过点P(a,0) 知直线l不垂直于x轴.设直线l的方程为y=k(x - a)+n,代入得b2x2+a2(kx+n - ak)2- a2b2=0,整理得(a2k2+b2)x2+2a2k(n-ak)x+a2(n-ak)2-a2b2=0.设M(x1,y1),N(x2,y2),据韦达定理,得

又设直线PM,PN的斜率分别为k1,k2,则
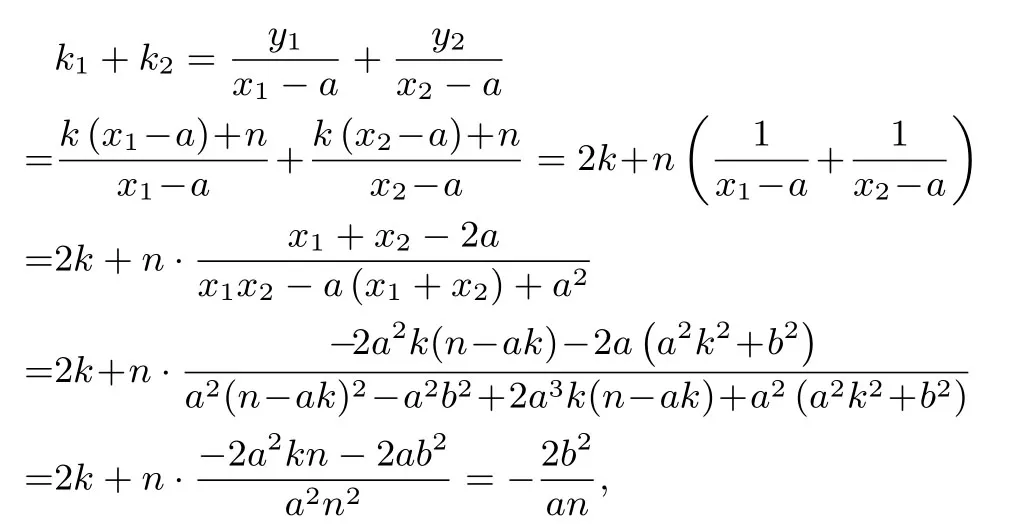
即直线PM,PN的斜率之和为定值
必要性:若直线PM,PN的斜率之和为定值显然当直线l垂直于x轴时,直线PM,PN的斜率之和k1+k2=0 与条件不符.故直线l不垂直于x轴,必与直线x=a相交.设其交点为(a,t)(显然0,否则点P与点M或N重合),即直线l过点(a,t).据充分性所证,得直线PM,PN的斜率之和又由直线PM,PN的斜率之和为定值由此得t=n,即直线l过定点Q(a,n)(0).综上,结论1(1) 得证.
类似地,对于结论1(2),只要把上述证明中的“a”换为“-a”,可得直线PM,PN的斜率之和为定值的充要条件是直线l过定点Q(-a,n).证毕.
3.探究结论的横向推广
问题3以上结论揭示了椭圆的右、左顶点P与相应定点Q的内在联系,那么,双曲线、抛物线是否具有类似性质?
探究3经探究,可得双曲线、抛物线的结论.对于双曲线只要把结论1 证明中的“b2”换为“-b2”,可得
结论2已知P为双曲线的右或左顶点,常数0.不经过点P的直线l与双曲线交于M,N两点,则
(1) 若P(a,0) 为右顶点,则直线PM,PN的斜率之和为定值的充要条件是直线l过定点Q(a,n);
(2) 若P(-a,0) 为左顶点,则直线PM,PN的斜率之和为定值的充要条件是直线l过定点Q(-a,n).
对于抛物线y2=2px(p >0) 可得
结论3已知O为抛物线y2=2px(p >0)的顶点,常数0.不经过点O的直线l与抛物线交于M,N两点,则直线OM,ON的斜率之和为定值的充要条件是直线l过定点Q(0,n).
证明充分性:若直线l过定点Q(0,n),由直线l不经过点O知直线l不垂直于x轴.设直线l的方程为y=kx+n(0),代入y2=2px(p >0) 得(kx+n)2=2px,整理得k2x2-2(p-kn)x+n2=0.设M(x1,y1),N(x2,y2),据韦达定理,得又设直线OM,ON的斜率分别为k1,k2,则

必要性:若直线OM,ON的斜率之和为定值显然当直线l垂直于x轴时,直线OM,ON的斜率之和k1+k2=0,与条件不符.故直线l不垂直于x轴,必与直线x=0 相交.设其交点为(t,0)(显然0 否则点O与点M或N重合),即直线l过点(t,0).据充分性所证,得直线OM,ON的斜率之和又由直线OM,ON的斜率之和为定值得由此得t=n,即直线l过定点Q(0,n).综上可得直线OM,ON的斜率之和为定值的充要条件是直线l过定点Q(0,n).证毕.
以上通过对一道教学质量检测试题的分析,提出有意义的数学问题,探究新的结论,这有助于学生初步了解数学结论产生的过程,体验创造的激情,建立严谨的态度和不怕困难的科学精神;有助于学生勇于质疑和善于反思的习惯,培养学生发现、提出、解决问题的能力;有助于发展学生的创新意识和创造能力.

