路堤荷载作用下斜坡地基侧向变形计算分析

刘晓华，韦彬，唐皓，戴智颖，赵炼恒

路堤荷载作用下斜坡地基侧向变形计算分析

刘晓华1，韦彬1，唐皓1，戴智颖1，赵炼恒2

(1. 深圳市综合交通设计研究院有限公司，广东 深圳 518003；2. 中南大学 土木工程学院，湖南 长沙 410075)

为探究斜坡地基在路堤荷载作用下的侧向变形，在Boussinesq和Cerruti集中力下半无限体侧向变形弹性解的基础上，运用积分思想，推导出斜坡地基在路堤荷载作用下的侧向位移。将路堤荷载分解为平行于斜坡和垂直于斜坡2个方向，分别推导出地基在平行和垂直于斜坡的各种荷载下的侧向变形理论解析解，最后依据叠加原理，将平行于斜坡表面和垂直于斜坡表面的荷载引起的侧向变形进行叠加，得出斜坡地基在路堤荷载作用下的侧向变形解析解。研究结果表明：对于斜坡上侧地基的土体，水平荷载引起的侧向变形可在一定程度上减小侧向变形的峰值，但对于斜坡下侧地基土体，水平荷载引起的侧向变形则会增大侧向变形的峰值。

斜坡地基；路堤荷载；侧向变形；解析解

近年来，我国对基础设施建设越来越重视，公路建设事业得到了迅速发展。截止2018年底，我国公路里程累计达到484.65万公里，其中，高速公路里程更是达到了14.26万公里，里程和规模都稳居世界第一位。公路里程增加的同时，公路灾害所造成的损失也越来越大。在造成公路灾害的众多原因之中，路基的沉降是其中重要的一个。一方面，路基沉降会引起路面凹陷，造成路面材料剥落，使路面出现坑槽，对行车安全性和行车舒适性带来危害，并且减少道路的使用寿命；另一方面，在山岭地区，修建在斜坡上的路基沉降还可能会引起地基变形，甚至诱发路堤沿接触面下滑，更严重的引起滑坡灾害，造成非常严重的后果。目前，对于地基变形工程中多以监测为主，这虽然能够较为准确地反映地基的变形状态和结果，但监测只能在施工过程中或者施工后，监测的结果也只能作为后续施工的指导或者评价安全性能的指标，若是能事先计算出其变形并以此为参考，从设计到施工，都能节省一大笔不必要的开支，带来巨大的经济效益。然而，在对其变形计算的研究中，由于计算理论的不足，国内外学者大都采用模型分析或数值模拟的方法，很少有通过理论推导出解析解，从而计算出土体变形的。地基在路堤荷载的作用下会产生沉降和侧向变形，目前采用的沉降计算方法和所采用参数大都基于太沙基一维固结理论。该理论认为，地基的变形只在垂直方向进行，从而忽略了土体的侧向位移对沉降的影响，这与实际情况明显不符且会带来较大的计算误差。另外，土体侧向变形的研究对象仅停留在水平地基，对斜坡形式的地基却鲜有研究。目前，随着地铁、高铁、大型建筑的大量建设，对沉降的监测和控制愈发重要，地基中土体的侧向位移引发的沉降不可忽视[1−4]。国内外研究人员从模型试验、工程实践、数值模拟、理论计算等方面入手对土体侧向变形进行研究取得了显著成果。曾国熙[5]基于Boussinesq竖向集中力下的解析解，在泊松比ν=0.5的条件下，推导出多种形式垂直荷载情况下土基在变形阶段侧向位移的解析式。Tavenas等[6]以多组路基侧向变形的实测数据为基础，将统计数据进行归一化处理，发现土体的侧向变形随深度呈弓形状。屠毓敏等[7]运用有限元的方法分析路堤沉降，发现土的侧胀性对土工结构的应力和变形影响较大，进一步证实了侧向位移沉降在路基的沉降分析中是不可以忽略的。刘增贤等[8]基于现场实测数据进行分析，发现侧向挤出产生的沉降在总沉降中占有相当大的比例，并讨论了影响侧向挤出的主要因素。陈晖[9]以工程实例为基础，针对固结沉降建立预测模型，对侧向位移沉降进行预测，提出计算侧向位移沉降的方法，并对常见路基处理方法进行评价。肖红兵等[10−11]基于Boussinesq竖向作用力下地基侧向位移的弹性理论解，采用积分方式导出了侧向变形弹性解析解。陶峰[12]针对侧向变形引起的沉陷，采用沉降修正系数对沉降量进行修正，通过工程实例分析表明修正系数具有较高的准确性。刘光秀等[13]基于Boussinesq弹性理论解，推导饱和黏土地基侧向位移计算公式，分析最大侧向位移的产生位置，并通过有限元探究土体泊松比与地基侧向变形的关系，理论解析解与模拟结果比较符合。刘光秀等[14]以平面应变的角度切入，推导出了路基荷载下地基的侧向变形理论解。然而，目前现有文献的研究对象大都是水平地基，鲜有对斜坡路堤荷载作用下地基的侧向变形规律及其对地基沉降的影响的研究。本文在已有研究成果的基础上研究斜坡地基的侧向变形，推导斜坡地基在各种作用力下的变形解析解，并分析理论解析解的正确性。研究成果可为相关实际工程提供理论依据。

1 斜坡路堤下地基变形分析坐标系建立

以中点为原点，建立坐标系，如图1所示。将路堤荷载划分为4部分，分别计算每部分荷载引起的地基侧向变形，然后利用叠加原理将侧向变形叠加，路堤荷载划分如图2所示。另外，将每一部分的荷载均分解为垂直于斜坡表面的分力(用表示)和平行于斜坡表面的分力(用表示)。

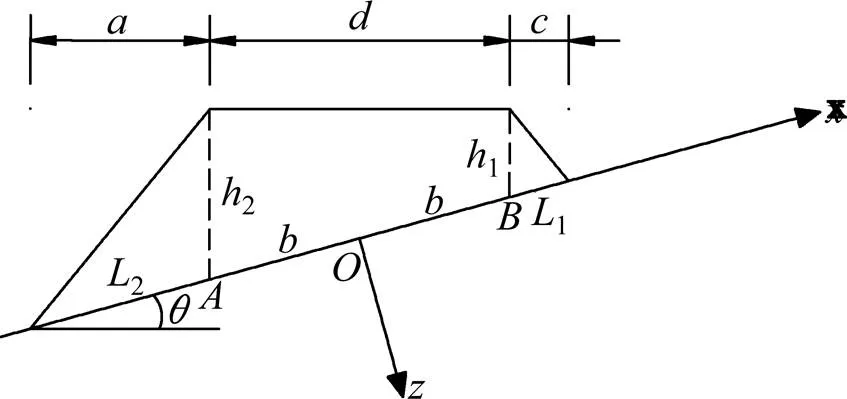
图1 建立坐标系

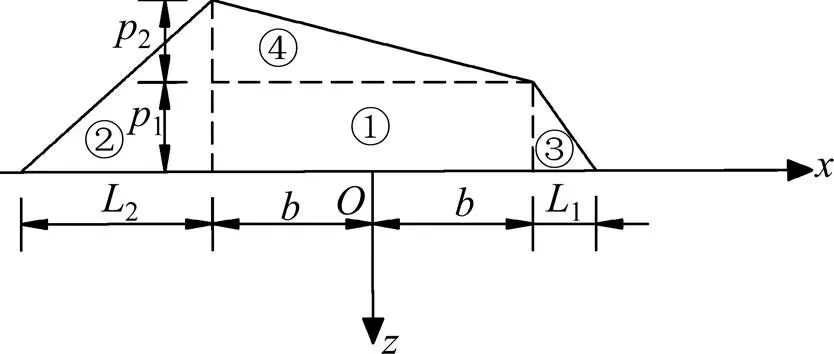
图2 荷载示意图

图2中，1和2表示荷载值；为半幅路面在斜坡上对应的距离；1和2分别为两侧边坡范围在斜坡上的对应距离。

各参数之间的关系为：

2 垂直斜坡方向分力作用下地基侧向变形

根据文献[15]，竖向荷载作用下土体的侧向变形可由布辛奈斯克解多次积分获得。

2.1 条形均布荷载作用下土体侧向变形

均布条形荷载(如图3)作用下土体中任意一点(,)处的侧向变形为：

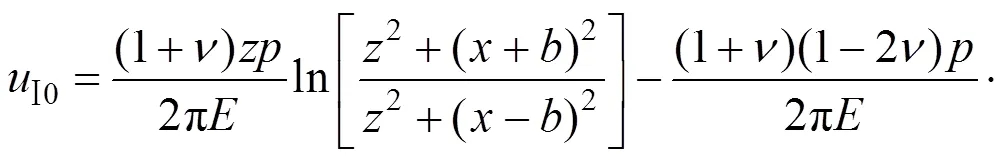
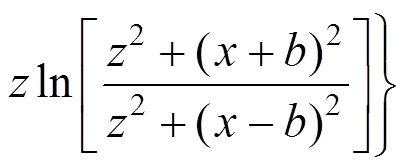
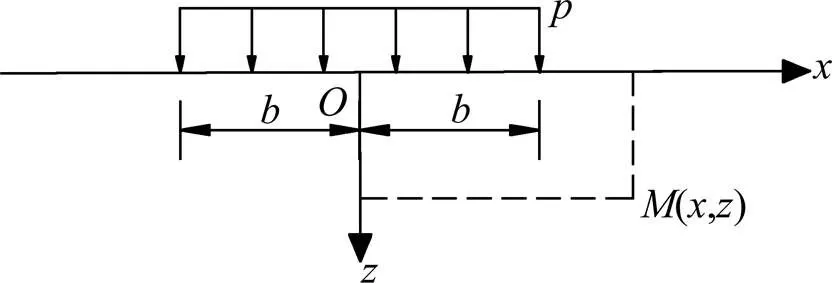
图3 条形分布荷载

2.2 三角形分布条形荷载作用下土体侧向变形计算

三角形荷载可分为Ⅱ型三角形荷载(如图4)和Ⅲ型三角形(如图5)2种情况。

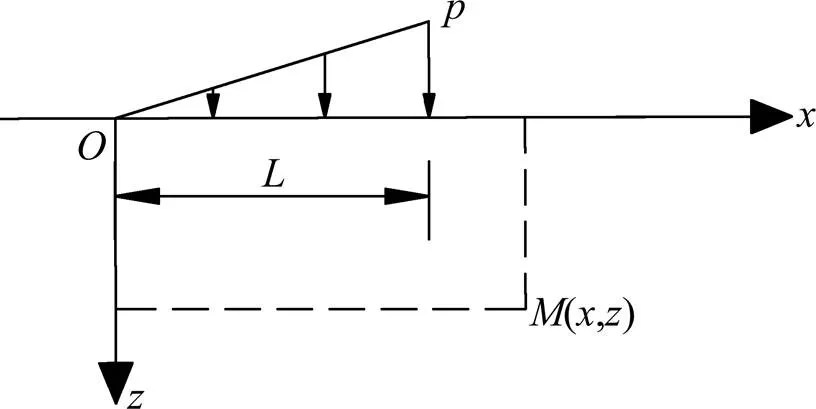
图4 Ⅱ型三角形分布荷载

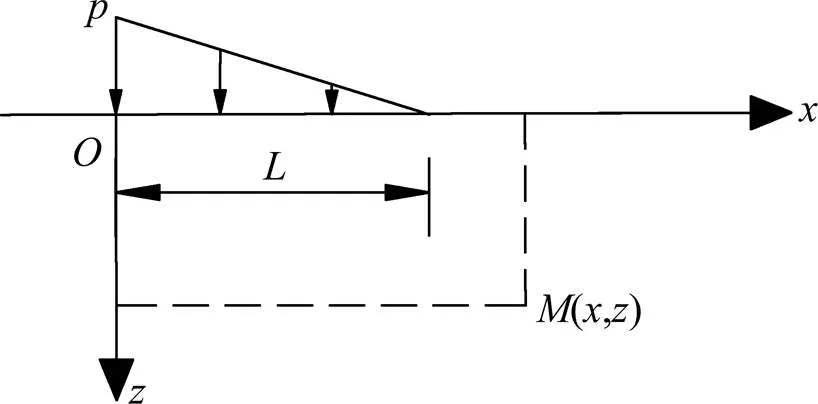
图5 Ⅲ型三角形分布荷载

Ⅱ型三角形分布荷载作用下土体中任意一点(,)处的侧向变形为：

Ⅲ型三角形分布荷载作用下土体中任意一点(,)处的侧向变形为：

2.3 垂直于斜坡表面的路堤分荷载作用下土体侧向位移计算

荷载①为均布荷载，相对图3所示的坐标系而言，坐标无变化，荷载大小为1。在荷载①垂直于坡面的分力的作用下地基土体中任意一点(,)处的侧向变形为：

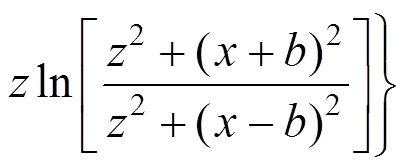
荷载②为Ⅱ型三角形荷载，相对图4所示的坐标系而言，坐标左移(+2)个单位，荷载大小为(1+2)。在荷载②垂直于坡面的分力的作用下斜坡地基土体中任意一点(,)处的侧向变形为：

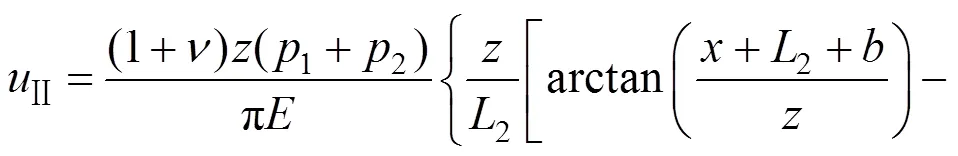
荷载③为Ⅲ型三角形荷载，相对图5所示的坐标系而言，坐标右平移个单位，荷载为1。在荷载③垂直于斜坡坡面的分力的作用下地基土体中任意一点(,)处的侧向变形为：

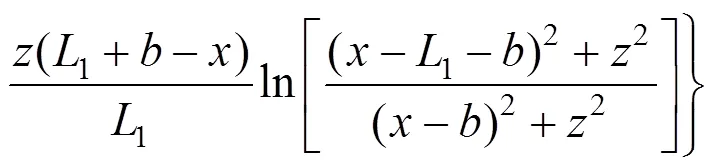
荷载④为Ⅲ型三角形荷载，相对图5所示的坐标系而言，坐标右移了个单位，荷载大小为2。在荷载④垂直于坡面的分力的作用下土体中任意点(,)处的侧向变形为：

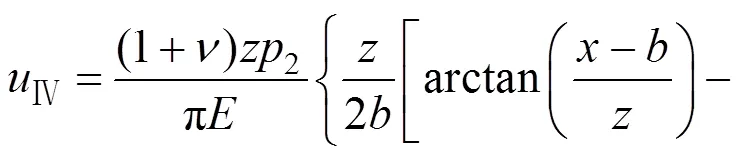
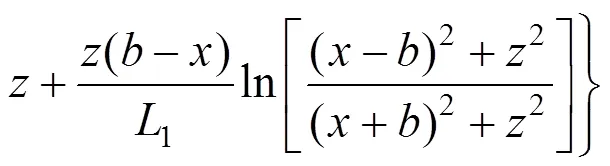
综上，由式(5)~(8)可得，垂直于斜坡表面的路堤分荷载作用下，地基的侧向变形如下式(9)所示：

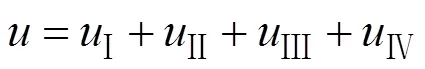
3 平行斜坡分力作用下地基侧向变形计算

3.1 线荷载作用下土体侧向应力、应变及侧向变形

如图6所示，半无限弹性体表面作用集中水平力，则任一点的应力按Cerruti解表达式如 下[15]：

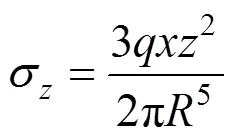
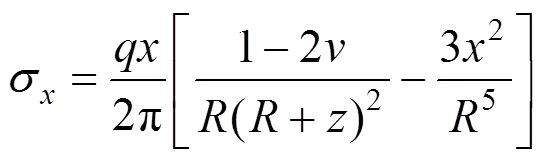
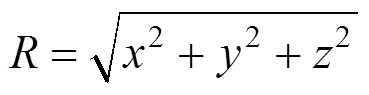
图6 水平方向集中力荷载作用示意图

在地基表面作用无限长均布线荷载时，荷载沿平面对称，对式(10)和式(11)进行积分可得平面内任意点(,)的竖向应力与侧向应力分别为：

根据广义胡克定律，且由=0知线荷载下点(,)处轴侧向应力σ=(+)，则点(,)处轴侧向应变为：

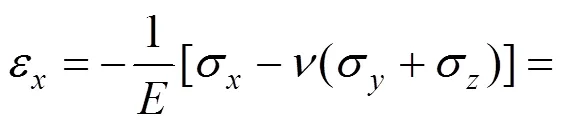
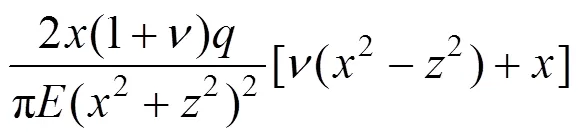
其中，是土体弹性模量，负号是指背离荷载方向的侧向应变为正值。

因此，(,)处的侧向变形x可由式(14)在轴方向上积分得到：

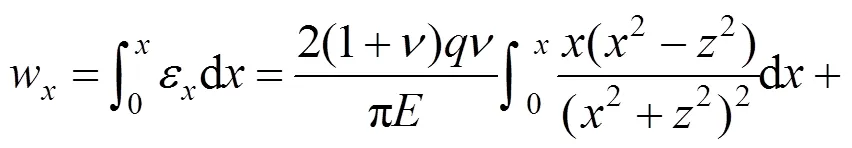
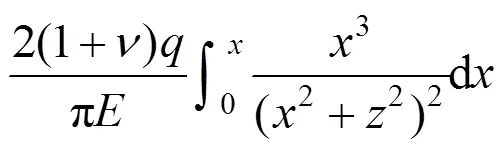
其中：

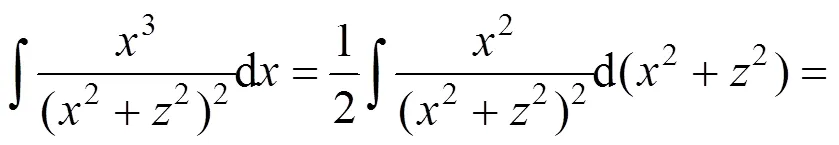
式中：0为任意常数。

将式(16)和(17)代入式(15)，并整理得：

式(18)为线荷载下土体任意点处侧向变形的解析解。

3.2 三角形分布条形荷载作用下土体的侧向应力、应变及侧向变形

三角形分布条形荷载有如图7所示2种情况(图中箭头仅表示应力大小，不表示方向)。

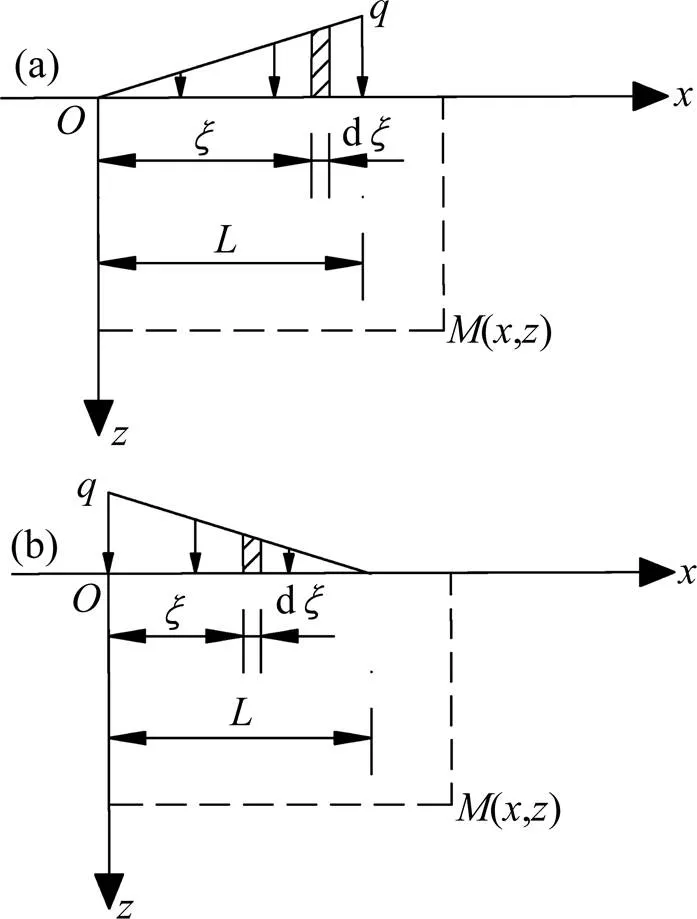
(a) Ⅱ型；(b) Ⅲ型

3.2.1 Ⅱ型三角形分布条形荷载作用下土体侧向应力、应变及侧向变形

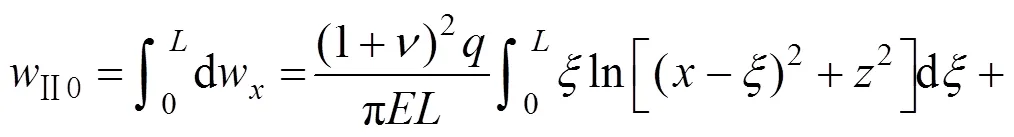
其中：

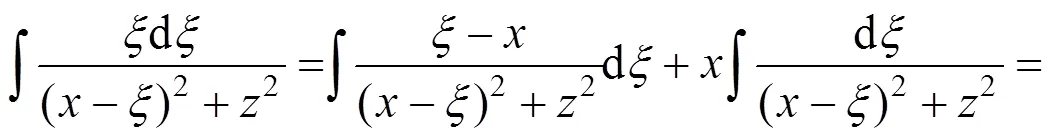
将式(20)~(21)代入式(19)并整理，得：

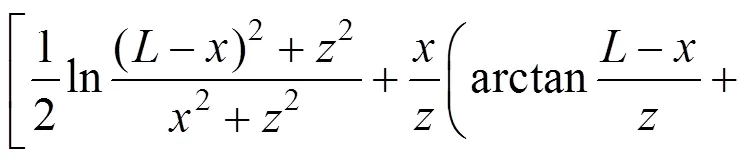
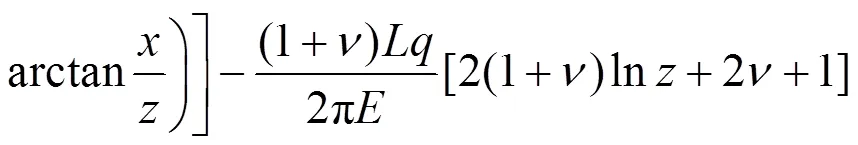
3.2.2 Ⅲ型三角形分布条形荷载作用下土体侧向应力、应变及侧向变形

对于Ⅲ型三角形荷载，用相同的方法可得：

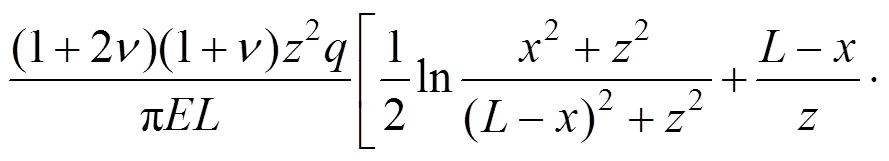
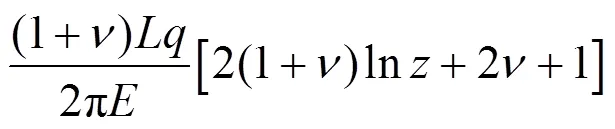
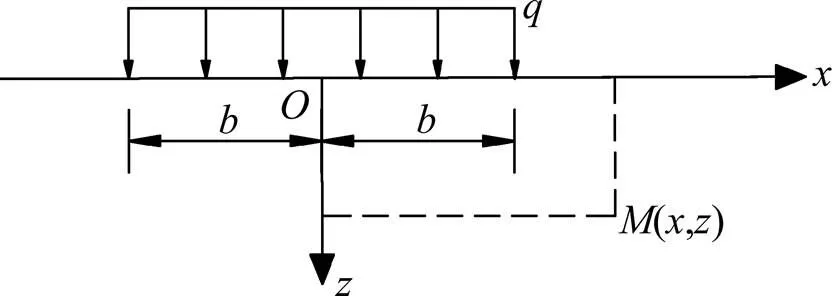
图8 条形水平均布荷载

3.3 条形均布荷载作用下土体侧向应力、应变及侧向变形

如图8(图中箭头仅表示应力大小，不表示方向)，地基表面作用条形均布荷载，基于式(10)和式(11)利用积分方法求解平面内任意点(,)竖向应力与侧向应力：

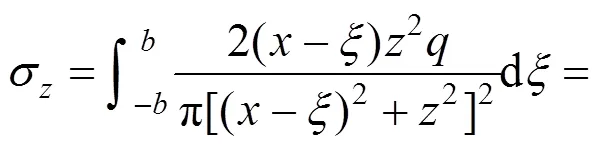
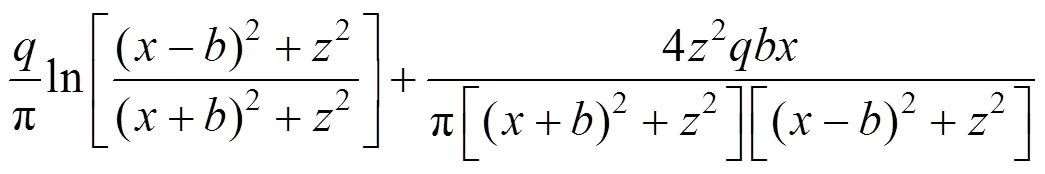
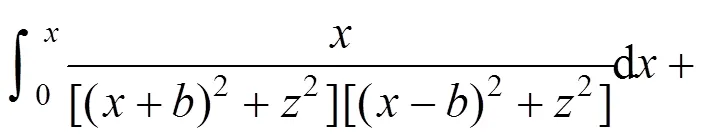
又：

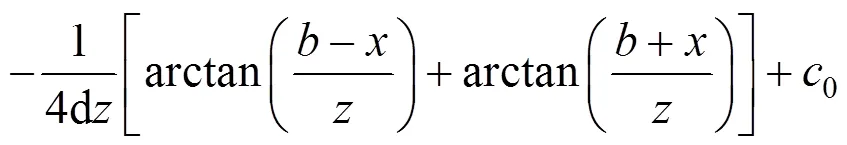
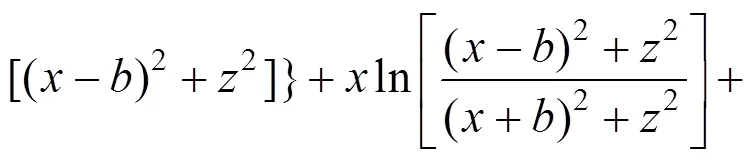
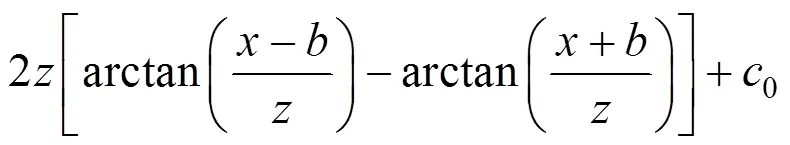
因此：

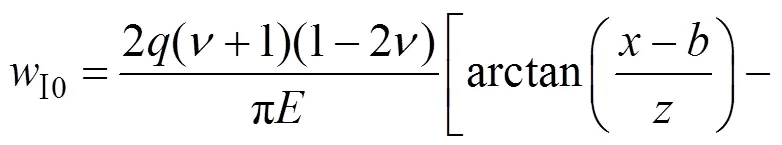
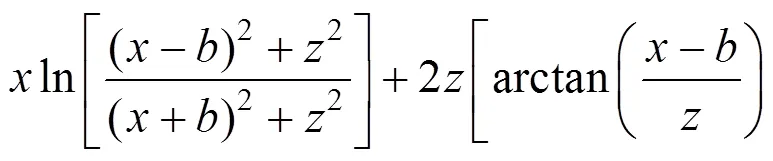
3.4 平行向分力作用下土体的侧向位移

荷载①为均布荷载，相对于原坐标系而言，坐标无变化，荷载大小为1。在荷载①平行于坡面的分力作用下地基任意一点(,)处的侧向变形：

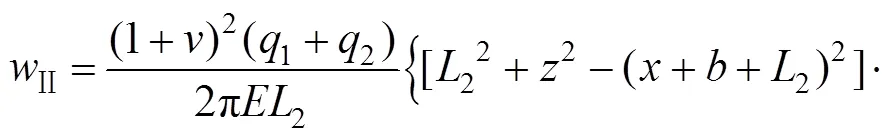
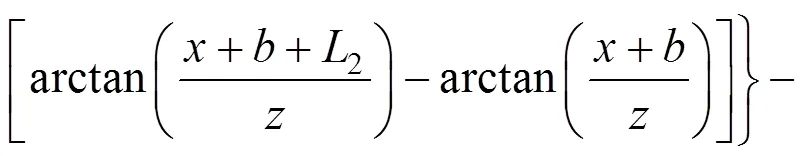
荷载③为Ⅲ型三角形荷载，相对原坐标系而言，坐标右移个单位，荷载为1。在荷载③平行于坡面的分力的作用下地基任意一点(,)处的侧向变形：

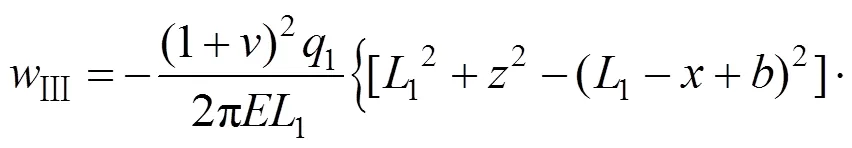
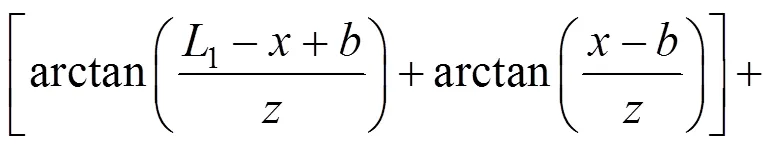
荷载④为Ⅲ型三角形荷载，相对原坐标系而言，坐标左移个单位，荷载大小为2。在荷载④平行于坡面的分力的作用下地基任意一点(,)处的侧向变形：

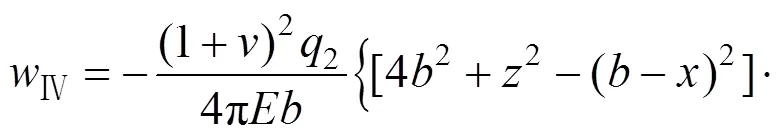
因此，平行向分力作用下地基的侧向变形为：

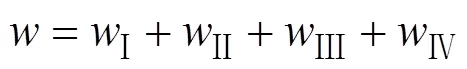
4 斜坡路堤荷载下地基的侧向变形求解

综上，斜坡路堤荷载下地基的侧向变形为平行于斜坡表面和垂直于斜坡表面的2个路堤分荷载分别作用下地基的侧向变形之和，即：

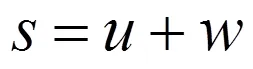
上面的公式叠加后会比较复杂，但由于表达式都为显式解析解，因此也很容易利用计算机编程进行计算。

5 实例验证

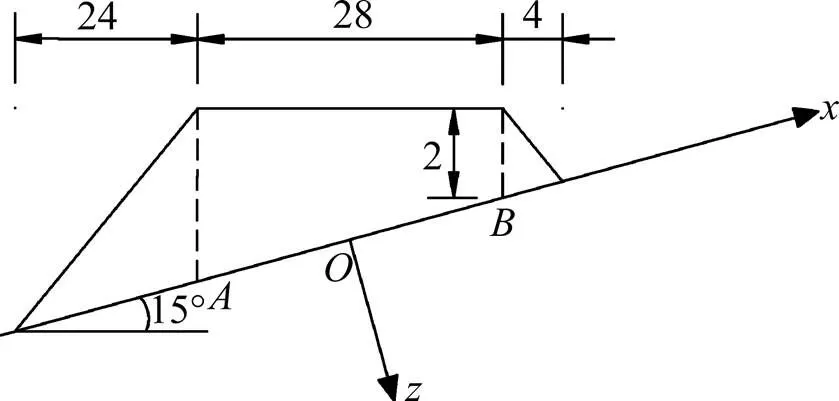
为验证式(37)计算结果的合理性，结合某高速公路软土路基段的侧向变形进行分析。设计路堤顶面宽度为=28 m，左边坡宽度为=24 m，右边坡宽度为=4 m，路堤右路肩与斜坡表面距离1=2 m，填土均重度=20 kN/m3，斜坡倾角=15°，地基土弹性模量=2.10 MPa，泊松比=0.4，路堤简图如图9所示。

分别取坡中、右坡脚、右坡肩处沿深度的土体水平位移计算结果进行分析，见图10。

单位：m

由图10可知，在路堤垂直荷载分力的作用下，地基某一竖直线上土体的侧向变形沿深度呈弓状，且侧向变形最大值在地表下土体某深度处，与已有研究结果吻合[6]。而路堤水平荷载分力作用下地基同一竖直线上土体的侧向变形沿深度逐渐增大，但增大速率逐渐减小，在深处逼近于某一固定值。路堤从右至左，水平荷载分力对土体侧向变形的影响越来越大，这是由于斜坡左低右高，路基表面右侧的水平分力所引起土体的侧向变形会改变左侧土体的应力状态，使左侧的土体产生更大的侧向位移，因此左侧的路堤下土体受平行荷载引起的变形更大。

另外可以看出，对于斜坡上侧路基的土体，水平荷载引起的侧向变形可在一定程度上减小侧向变形的峰值，但对于斜坡下侧路基土体，水平荷载引起的侧向变形则会增大侧向变形的峰值。因此，对于路堤荷载作用下的斜坡地基，处于斜坡下侧部分的土体更容易发生破坏，在实际工程中应采取工程措施对下部地基进行加固。

6 结论

1) 通过对半无限空间体的Boussinesq弹性解和Cerruti弹性解进行积分，分别导出了斜坡地基在垂直于斜坡表面和平行于斜坡表面的多种不同类型荷载下作用下的侧向变形的理论解析解。推导获得的显式解析式利用计算机编程很容易进行计算，工程实际应用价值较高。

2) 由于水平荷载分力的影响，斜坡下侧部分的路基土体的侧向变形受路堤荷载的影响更大，引起侧向变形峰值更大，更容易发生破坏。在实际工程中有必要加大对斜坡下侧路基土体的变形监测，同时对下侧路堤进行适当支挡结构设计以保障斜坡路堤的整体稳定性。

[1] 马时冬. 路堤下软黏土地基的侧向位移[J]. 华侨大学学报(自然科学版), 1995, 16(2): 165−167. MA Shidong. Lateral displacement of soft clay foundation under embankment[J]. Journal of Huaqiao University (Natural Science), 1995, 16(2): 165−167.

[2] 王峰, 金武, 王宏坤, 等. 考虑侧向变形影响的客运专线路基沉降的修正[J]. 岩土工程学报, 2010, 32(增2): 245−248. WANG Feng, JIN Wu, WANG Hongkun, et al. Subgrade settlement correction of passenger dedicated line considering lateral deformation[J]. Journal of Geotechnical Engineering, 2010, 32(Suppl 2): 245−248

[3] 杨武, 曹文昭, 董佳竹. 考虑侧向变形的客运专线路基沉降特性研究[J]. 土木工程与管理学报, 2012, 29(3): 99−103. YANG Wu, CAO Wenzhao, DONG Jiazhu. Study on subgrade settlement characteristics of passenger dedicated line considering lateral deformation[J]. Journal of Civil Engineering and Management, 2012, 29(3): 99− 103.

[4] 陶峰. 考虑侧向变形影响的路基沉降计算方法修正[J].山西交通科技, 2015(6): 28−30. TAO Feng. Correction of subgrade settlement calculation method considering lateral deformation[J]. Shanxi Transportation Technology, 2015(6): 28−30.

[5] 曾国熙. 垂直荷载下软粘土地基的侧向变形[J]. 浙江大学学报, 1962(1): 93−124. ZENG Guoxi. Lateral deformation of soft clay foundation under vertical load[J]. Journal of Zhejiang University, 1962(1): 93−124.

[6] Tavenas F, Leroueil S. The behavior of embankments on soft foundations[J]. Canadian Geotechnical Journal, 1980, 17: 236−259.

[7] 屠毓敏, 郑坚. 考虑土体侧胀性的路堤沉降分析[J]. 中国公路学报, 2002(1): 29−31. TU Yumin, ZHENG Jian. Analysis of embankment settlement considering soil lateral expansion[J]. Chinese Journal of Highway, 2002(1): 29−31.

[8] 刘增贤, 汤连生. 路堤荷载下软土侧向挤出沉降分析[J]. 工程勘察, 2003(2): 1−4. LIU Zengxian, TANG Liansheng. Analysis of lateral extrusion settlement of soft soil under embankment load [J]. Engineering Survey, 2003(2): 1−4.

[9] 陈晖. 侧向性位移对路堤的影响分析[J]. 山西建筑, 2016, 42(7): 161−162. CHEN Hui. Influence analysis of lateral displacement on embankment[J]. Shanxi Building, 2016, 42(7): 161−162.

[10] 肖红兵, 蒋关鲁. 考虑路基侧向变形的沉降计算方法[J]. 公路工程, 2014, 39(1): 69−72. XIAO Hongbing, JIANG Guanlu. Settlement calculation method considering lateral deformation of roadbed[J]. Highway Engineering, 2014, 39(1): 69−72.

[11] 蒋关鲁, 兰维维, 肖红兵, 等. 路基荷载下地基侧向变形的计算方法[J]. 重庆大学学报, 2014, 37(2): 89−97. JIANG Guanlu, LAN Weiwei, XIAO Hongbing, et al. Calculation method of lateral deformation of subgrade under subgrade load[J]. Journal of Chongqing University, 2014, 37(2): 89−97.

[12] 陶峰. 考虑侧向变形影响的路基沉降计算方法修正[J].山西交通科技, 2015(6): 28−30. TAO Feng. Correction of subgrade settlement calculation method considering lateral deformation[J]. Shanxi Transportation Technology, 2015(6): 28−30.

[13] 刘光秀, 曹海莹, 李玉根. 竖向荷载下饱和黏土地基的侧向变形性状分析[J]. 中外公路, 2018, 38(2): 31−35. LIU Guangxiu, CAO Haiying, LI Yugen. Analysis of lateral deformation characteristics of saturated clay foundation under vertical load[J]. Journal of China & Foreign Highway, 2018, 38(2): 31−35.

[14] 刘光秀, 李玉根, 曹艳妮. 路堤荷载下地基的侧向变形计算分析[J]. 岩土力学, 2018, 39(12): 4517−4526, 4536. LIU Guangxiu, LI Yugen, CAO Yanni. Calculation and analysis of lateral deformation of foundation under embankment load[J]. Rock and Soil Mechanics, 2018, 39(12): 4517−4526, 4536.

[15] 李婕, 顿志林, 张学民, 等. 横观各向同性弹性地基塞露蒂问题的解析解[J]. 工程力学, 2007(增1): 70−74. LI Jie, DUN Zhilin, ZHANG Xuemin, et al. An analytical solution to the seluti problem for transversely isotropic elastic foundation[J]. Engineering Mechanics, 2007(Suppl 1): 70−74.

Calculation and analysis of lateral deformation of slope foundation under embankment load

LIU Xiaohua1, WEI Bin1, TANG Hao1, DAI Zhiying1, ZHAO Lianheng2

(1. Shenzhen Transportation Design & Research Institute, Shenzhen 518003, China; 2. School of Civil Engineering, Central South University, Changsha 410075, China)

In terms of foundation form, the horizontal foundation is mostly studied, but there is little research on slope foundation. In order to research the lateral deformation of slope foundation under embankment load, based on the Boussinesq and Cerruti semi-infinite elastic body under the concentrated force of integral solution of lateral deformation, this paper has deduced the formula of the lateral deformation of slope foundation by using the idea of integration. Firstly, the embankment load was decomposed to be parallel to the slope and vertical to the slope, and then the theoretical solution of the lateral deformation of the foundation under various loads parallel to and perpendicular to the slope was derived. Finally, according to the superposition principle, the lateral deformation of the slope foundation under the embankment load was obtained by superposing the two deformations. The calculation results show that the lateral deformation caused by horizontal load can reduce the peak value of lateral deformation to a certain extent for the soil on the upper side of the slope, but for the soil on the lower side of the slope, the peak value will increase.

slope foundation; embankment load; lateral deformation; analytical solution

TU433

A

1672 − 7029(2020)03 − 0582 − 10

10.19713/j.cnki.43−1423/u.T20190893

2019−06−14

贵州省科学技术厅科技支撑计划重点项目([2018]2815)；贵州省交通运输厅科技项目(2017-123-033，2018-123-040)

赵炼恒(1980−)，男，湖南益阳人，教授，博士，从事道路与铁道工程、岩土极限分析理论与应用等研究；E−mail：zlh8076@163.com

(编辑 涂鹏)