八轮AGV转向及运动控制特性分析

上海振华重工(集团)股份有限公司

1 引言

AGV(Automated Guided Vehicle，自动引导小车)是集装箱码头岸边集装箱起重机到堆场设备之间水平运输的关键设备，具有自动化程度高、灵活性强、安全性好、效率高等特点[1-2]。

近年来，AGV的研究工作得到了广泛的开展。Danwei等主要开展了四轮转向车辆轨迹方面的研究，利用转向系统的灵活性，将轨迹规划分解为速度规划及转向规划，同时考虑到车辆机械和驱动力矩等约束的限制[3]。任孝平等基于阿克曼原理对轮式移动机器人的运动学特性，建立了不考虑滑行、刹车等的轮式移动机器人的运动学模型，给出了描述机器人运动状态的转向角、航向角和转弯半径等物理量的数学公式[4]。T Le-Anh主要从车辆调度角度综述了自动导引车辆系统的设计与控制[5]。

相比于物流行业传统的双轮差分驱动以及带阿克曼连杆的四轮转向车辆，本文所研究的八轮独立转向车辆除基本直行行驶、90°转向及蟹行运动外，还支持横行及原地转向模式，其灵活的运动方式可作为目前集装箱自动化码头自动引导车的一种扩展形式。八轮180°回转电差速AGV的8个轮子被分成4组，每组2个轮子靠短驱动桥连接在一起，由电机独立驱动，且最大可实现110°转向运动。本文主要探讨了车辆在各种运行模式下车轮转向角度及轮速分配问题，在系统给定轨迹基础上设计了前后控制点路径跟踪控制算法，阐述了前后轴控制点目标转向角度及轮速计算方法，最后通过选取几组常见运行工况，对所述方法进行了验证。

2 转向及运动学模型分析

AGV在不同速度、不同带载情况下运行时，其动力学特性同样很重要，但是考虑到转向及行走等驱动装置建模复杂，且建模精度有限，通常采用加大系统设计功率以及通过设置不同配载情况下使用不用的加减速度来减少动力学特性带来的影响[6-7]，本文只讨论运动学模型问题。

为简化车辆运动学分析，假设在车辆的中心线和车轴的交点上存在2个虚拟车轮，图1为车辆在反对称转向模式下的示意图，其中φfl和φfr分别为前轴左侧和右侧的转向角，Φrl和φrr分别为后轴左侧和右侧的转向角，O为车辆中心点，也即为车辆转向中心与车辆中心线的交点[8-9]。车辆转向运动学模型为：

(1)

式中，(x1,y1)为车头侧车轴虚拟中心位置；θ为AGV的朝向角(逆时针为正方向)；B为车头侧和车尾侧车轴虚拟中心之间的距离；φ1和φ2为前后虚拟车轮转向角；v1为前轴虚拟车轮中心的速度。

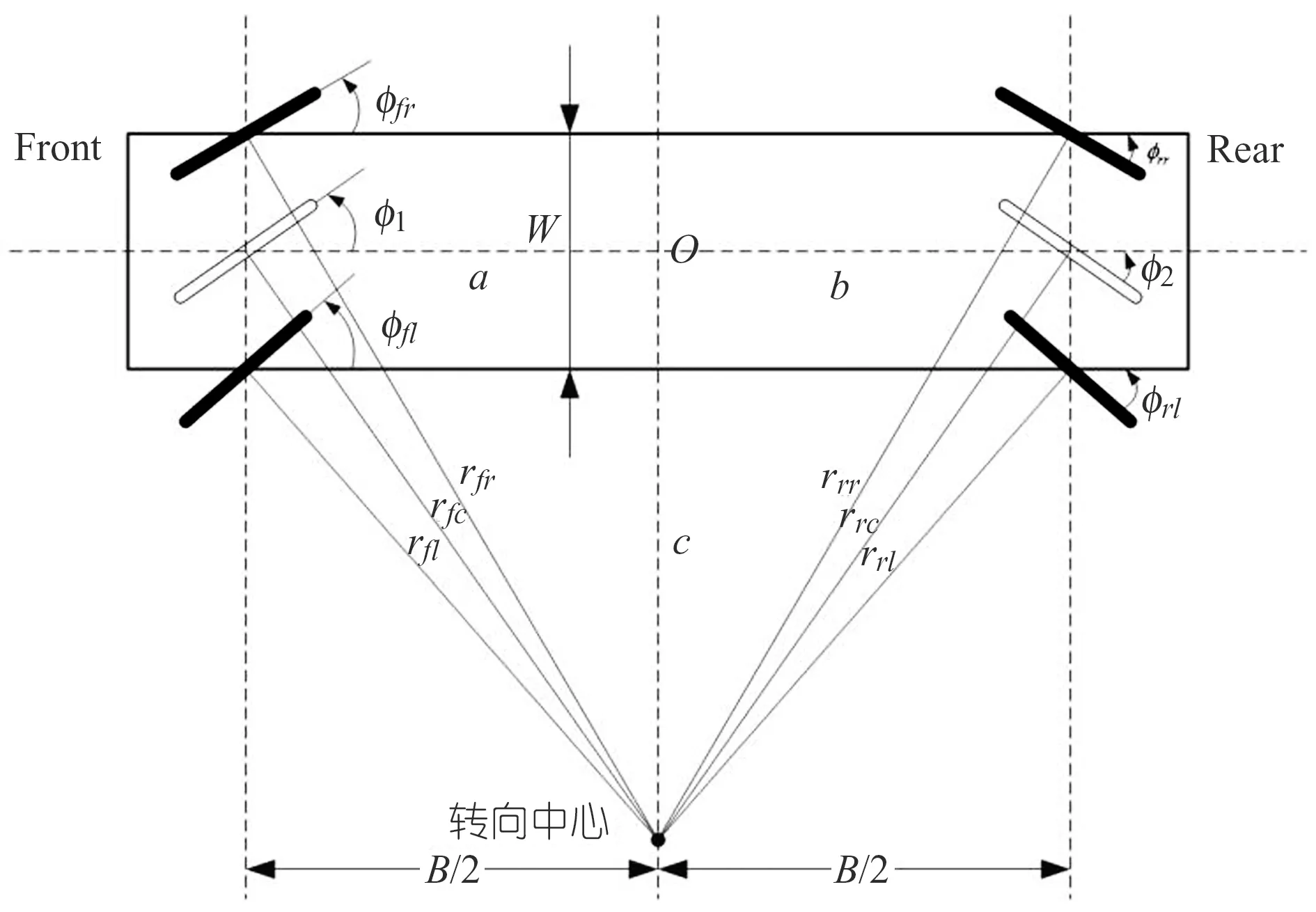
图1 反对称转向

假设前后车轴的虚拟合成角度和合成速度已经由运动控制模块计算得出，且分别为φ1、φ2、VF、VR，则四轮反对称转向模式下对应的4个轮子转角及转速分别如式(2)～(9)所示：

θfl_cmd=atan{Btanφ1/[B-0.5T(tanφ1-tanφ2)]}

(2)

θfr_cmd=atan{Btanφ1/[B+0.5T(tanφ1-tanφ2)]}

(3)

θrl_cmd=atan{Btanφ2/[B-0.5T(tanφ1-tanφ2)]}

(4)

θrr_cmd=atan{Btanφ2/[B+0.5T(tanφ1-tanφ2)]}

(5)

(6)

(7)

(8)

(9)

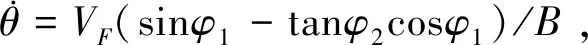
横行及蟹行模式下，4个轮子转向角度及轮子转速指令分别为:

θfl_cmd=θfr_cmd=θrl_cmd=θrr_cmd

(10)

Vfl_cmd=Vfr_cmd=Vrl_cmd=Vrr_cmd

(11)

原地转向模式下，4个轮子转向角度及轮子转速指令分别为：

θfl_cmd=-θfr_cmd=-θrl_cmd=θrr_cmd=atan(B/T)

(12)

Vfl_cmd=-Vfr_cmd=-Vrl_cmd=Vrr_cmd

(13)

各轮子转向角度经伺服驱动器控制的伺服电机带动转向机构转动，4组轮子独立转向。各轮子速度指令经过减速比和量纲转换后送入行走电机驱动器中。

3 前后车轴路径跟踪控制

考虑到车辆导航系统采用天线—磁钉系统测量AGV的绝对位置信息，即在AGV底盘的前端和后端，对称安装1对检测天线。为方便求取路径跟踪偏差信息，直角转弯以及蟹行运动模式下轨迹规划模块输出直接为前后天线目标路径，通过计算获得前后天线路径偏差信息，并将其输入运动控制单元，控制器输出经过折算后即为前后车轴的合成角度和合成速度，经过转向角度及转速分配后即可获得每个轮子转向角度及转速目标控制值。

运动控制的原理可以解释为斜行和反对称转向的组合。AGV在跟踪期望路径时，主要有2种误差：位置误差δd，即AGV中心点与期望路径垂直距离；航向角偏差δθ，即AGV方向角与期望路径垂足处切线方向夹角之间的差值。纠正横向路径偏差需要通过调整转向角进行修正，可采用斜行来补偿位置偏差，采用反对称转向来补偿航向角偏差，前后合成轮的修正量为：

δφ1=lim(δφ_min,Kcrabδd+Kturn1δθ

(14)

δφ2=lim(δφ_min,Kcrabδd-Kturn1δθ

(15)

式中，δφ_min为每次纠偏向右最大摆动值(负值)；δφ_max为每次纠偏向左最大摆动值(正值)；Kcrab、Kturn1,Kturn2分别为斜行及转向控制增益。

为实现小车精确定位，车轮速度采用分段减速控制方法。主动轮车轴目标速度由车辆加减速度特性，到目标点距离，环境及任务最大允许速度以及爬行距离决定，整个过程速度规划曲线见图2。其中adec为车辆减速度，Δs为到目标点距离(原地转向模式时也可作为到目标点的航向角偏差)，kp为比例控制增益，Vslow为爬行速度。

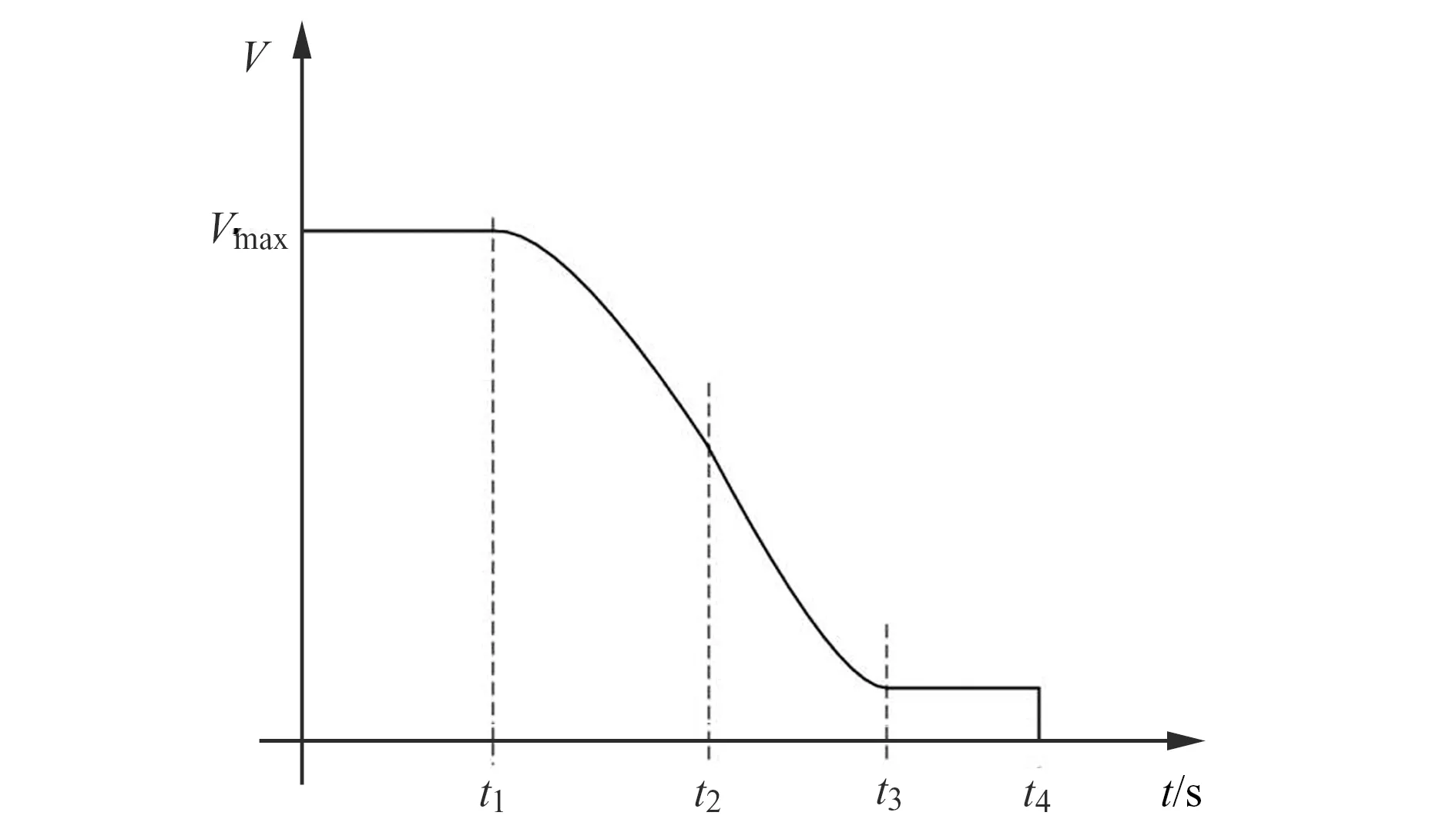
图2 减速控制曲线

首先根据AGV当前位置与目标位置之间的距离，匀速保持时间及驱动器加减速特性计算出本次行车指令AGV可能达到的最大运行速度Vmax。当Δs≤V2max/2adec时，采用匀减速控制策略，之后切换至比例速度控制模式。待车辆运行至距离目标位置为爬行距离后，保持为爬行速度，进一步到达制动距离时，给出制动命令。

考虑到运动过程中前后轴速度匹配问题，从动轮车轴给定速度为：

VR=VFcosφf/cosφr

(16)

车辆控制器根据导航控制器给定的电机转速参考值对前后电机进行协调控制，即通过监控电机的电流和电压实时计算车头车尾2台电机的输出功率。当两者输出功率之差大于一定阈值时，表明车尾输出力不足，这时电控控制器就在车尾电机转速给定参考值基础上，逐渐增大车尾电机的转速参考值，直到2台电机的输出功率之差小于阈值。

4 实验结论

为了验证所设计控制器有效性，选取几组典型工况进行测试。

4.1 工况一：直角转弯

AGV主要依靠90°直角转弯来改变路径行驶方向。给定条件为：最大转弯运行速度2.0 m/s，转弯半径16 m，采样周期10 ms。从图3～图8可以看出车桥给定速度及角度跟踪效果良好，整个行车过程中前后天线横向路径偏差保持在较小范围，停车时横向偏差10 mm左右。

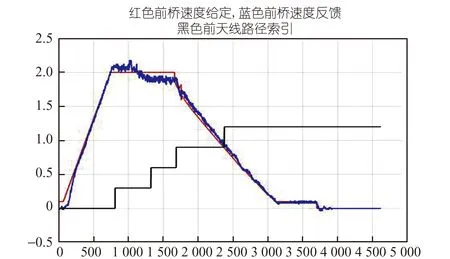
图3 主动轮速度给定及反馈

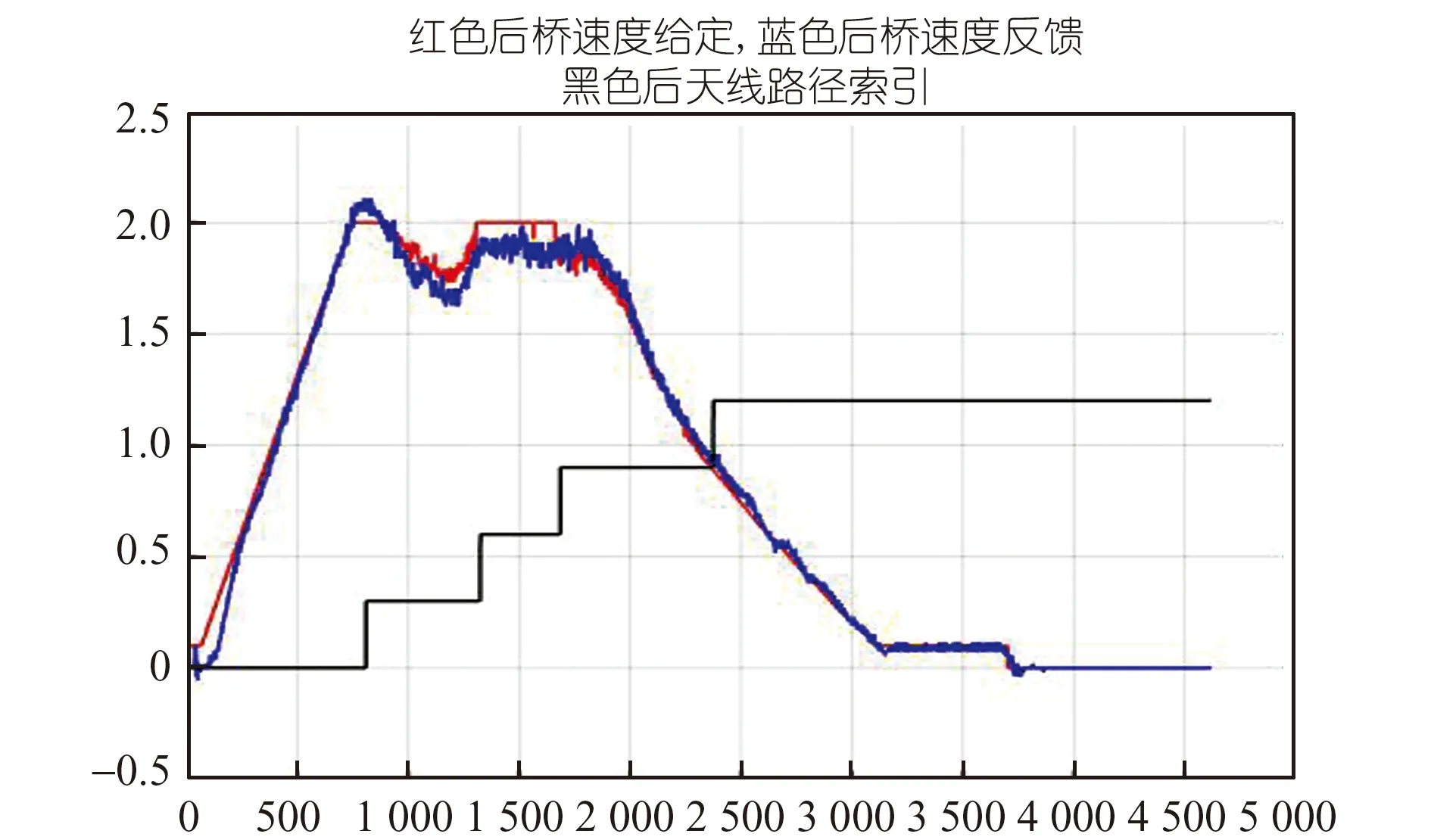
图4 从动轮速度给定及反馈

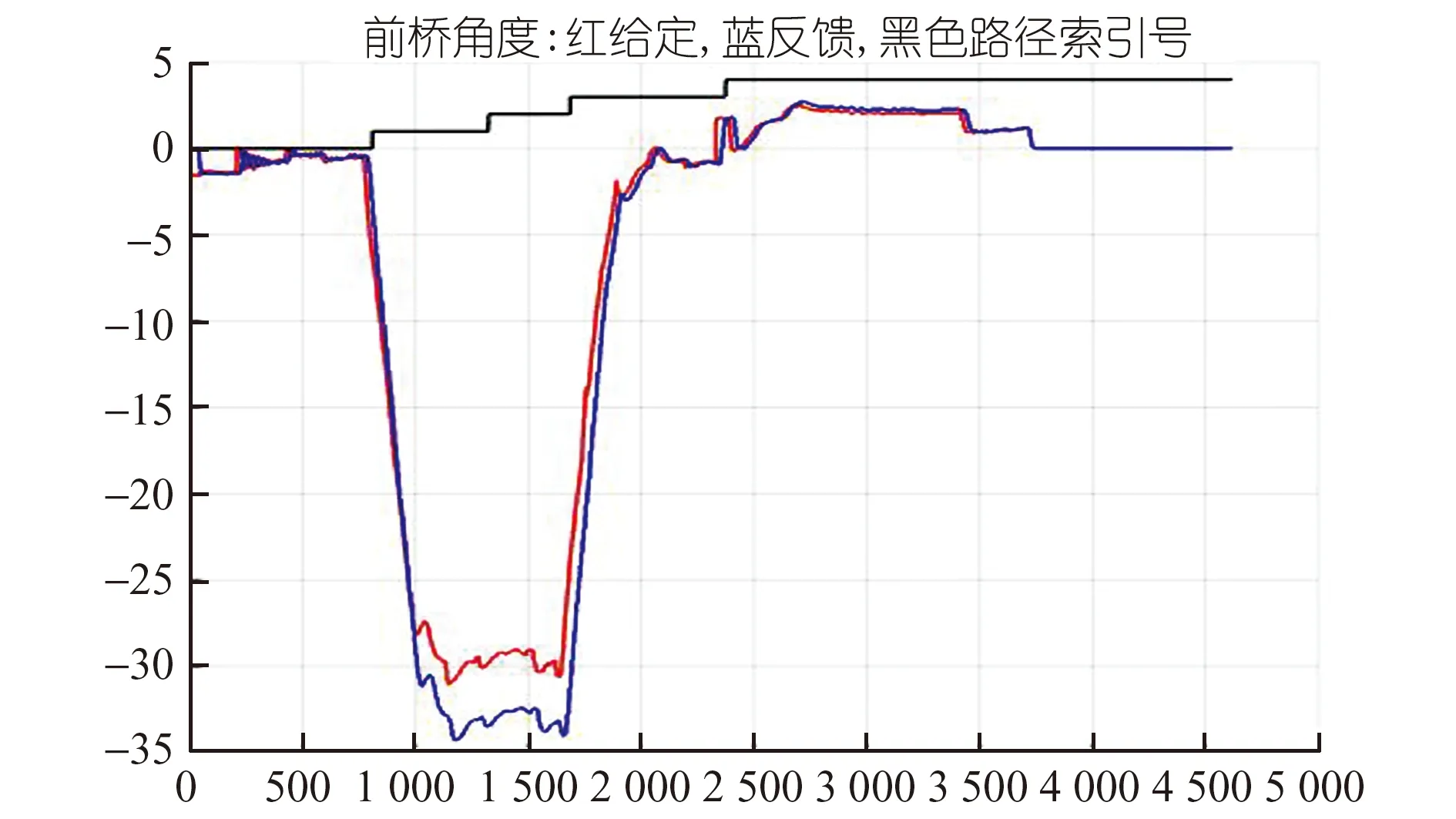
图5 主动桥给定角度

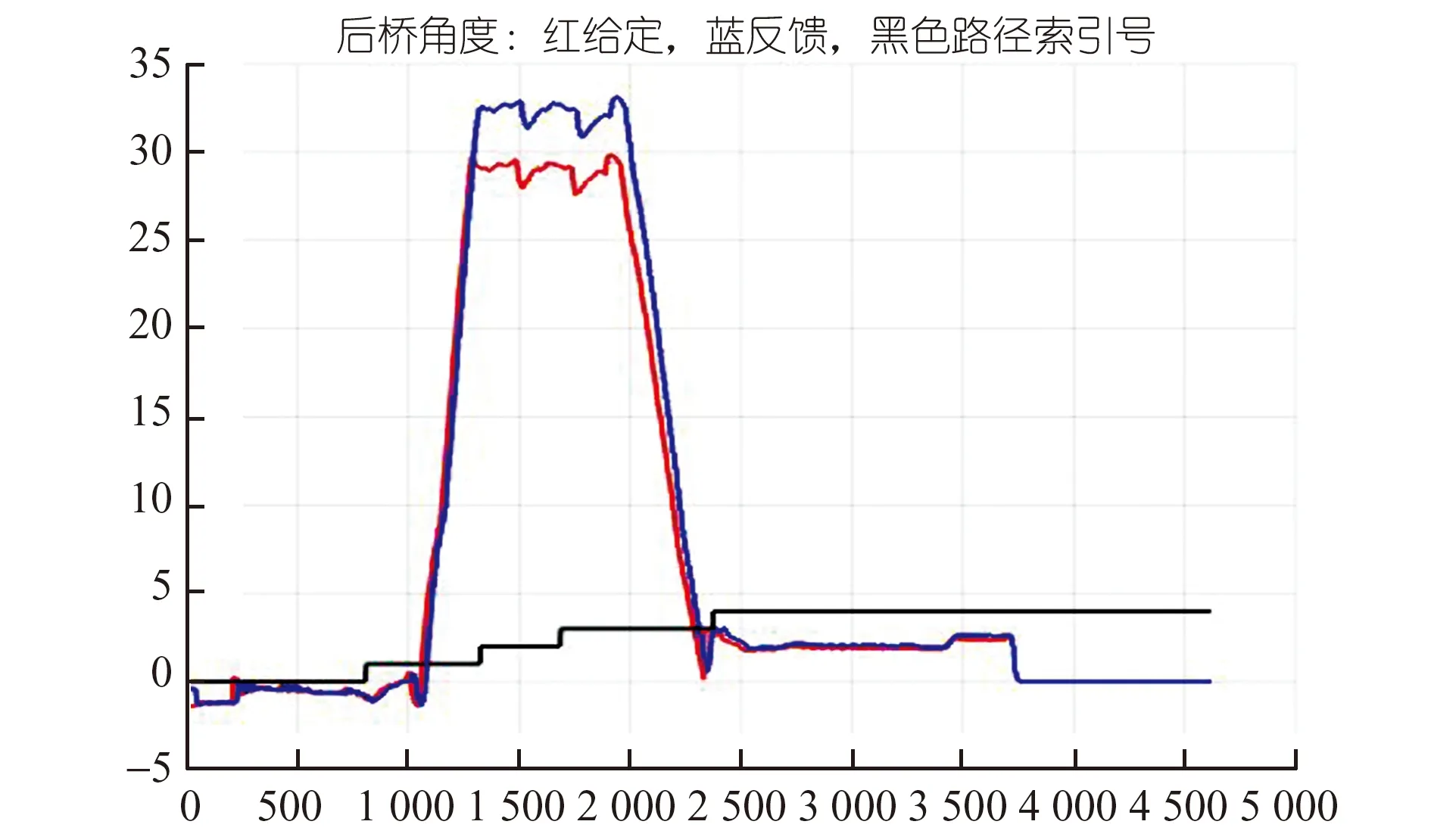
图6 从动桥给定角度

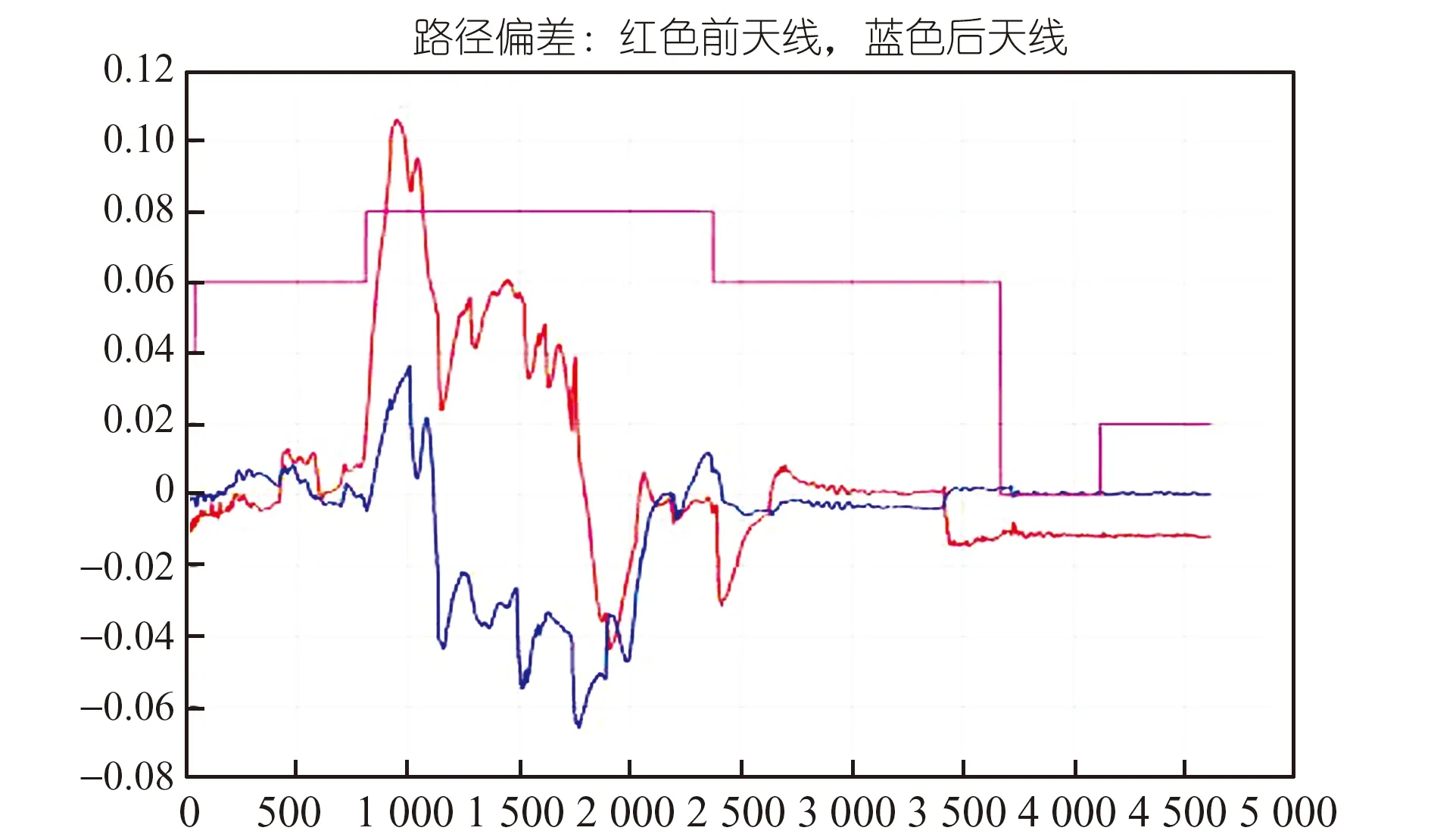
图7 前后天线横向路径偏差

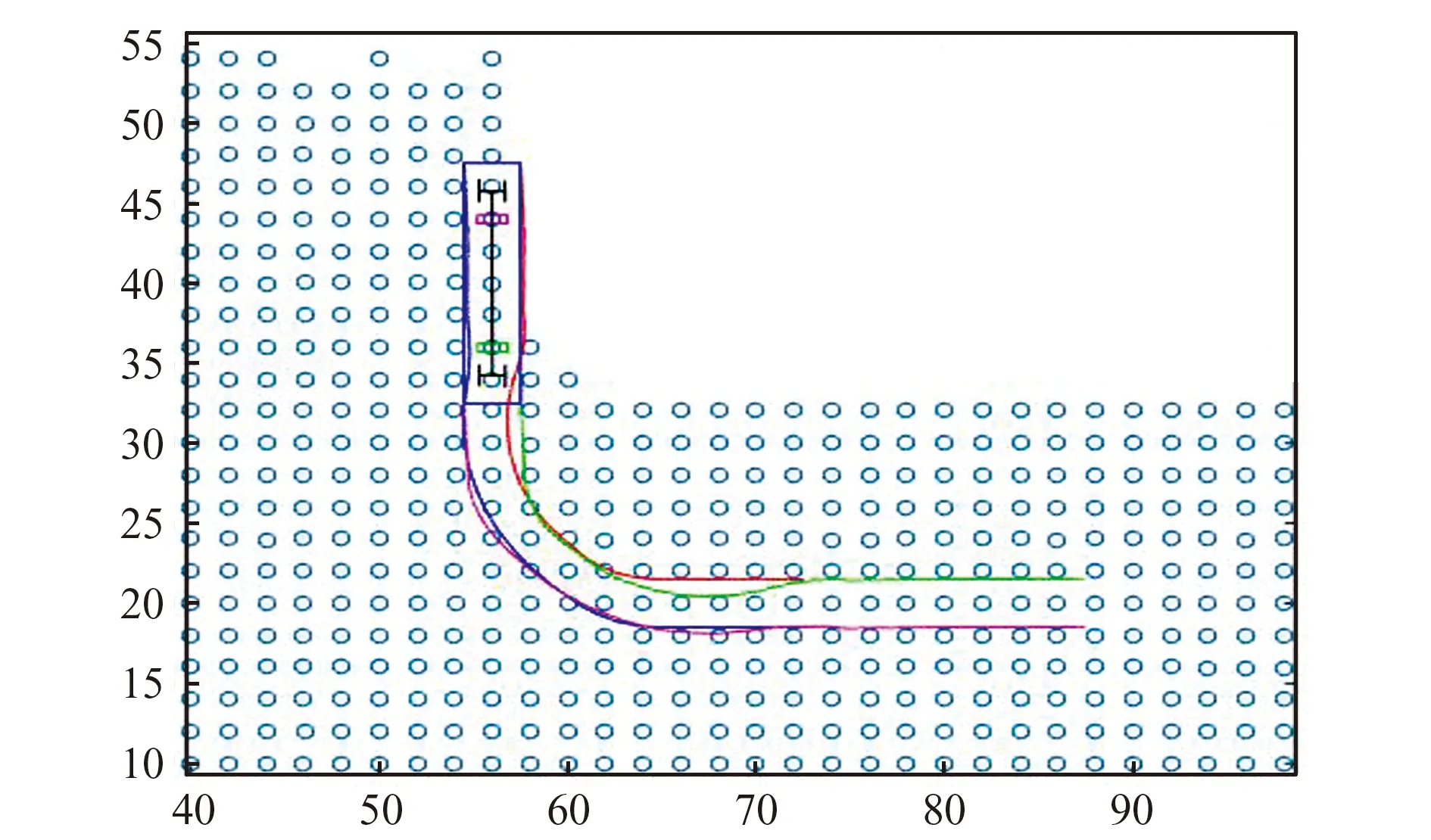
图8 直角转弯运行轨迹

4.2 工况二：横行模式

横行模式主要用于车辆在狭窄空间内进行变道作业，整个过程中车辆处于横向移动状态。最大横向移动速度1 m/s，变道宽度4 m。由图9～图12可以看出，在当前运行速度下，整个行车过程中车辆航向角变化较小，停车时行车方向(Y)位置偏差小，非行车方向位置偏差(X)为80 mm左右，和前后车桥一致性以及转向零位有一定关系。

图9 车辆中心点横坐标X

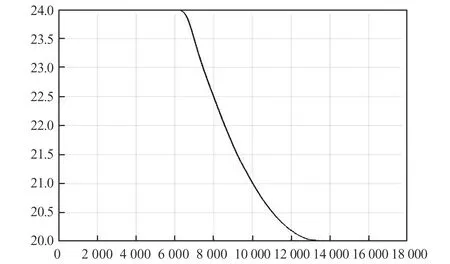
图10 车辆中心点横坐标Y

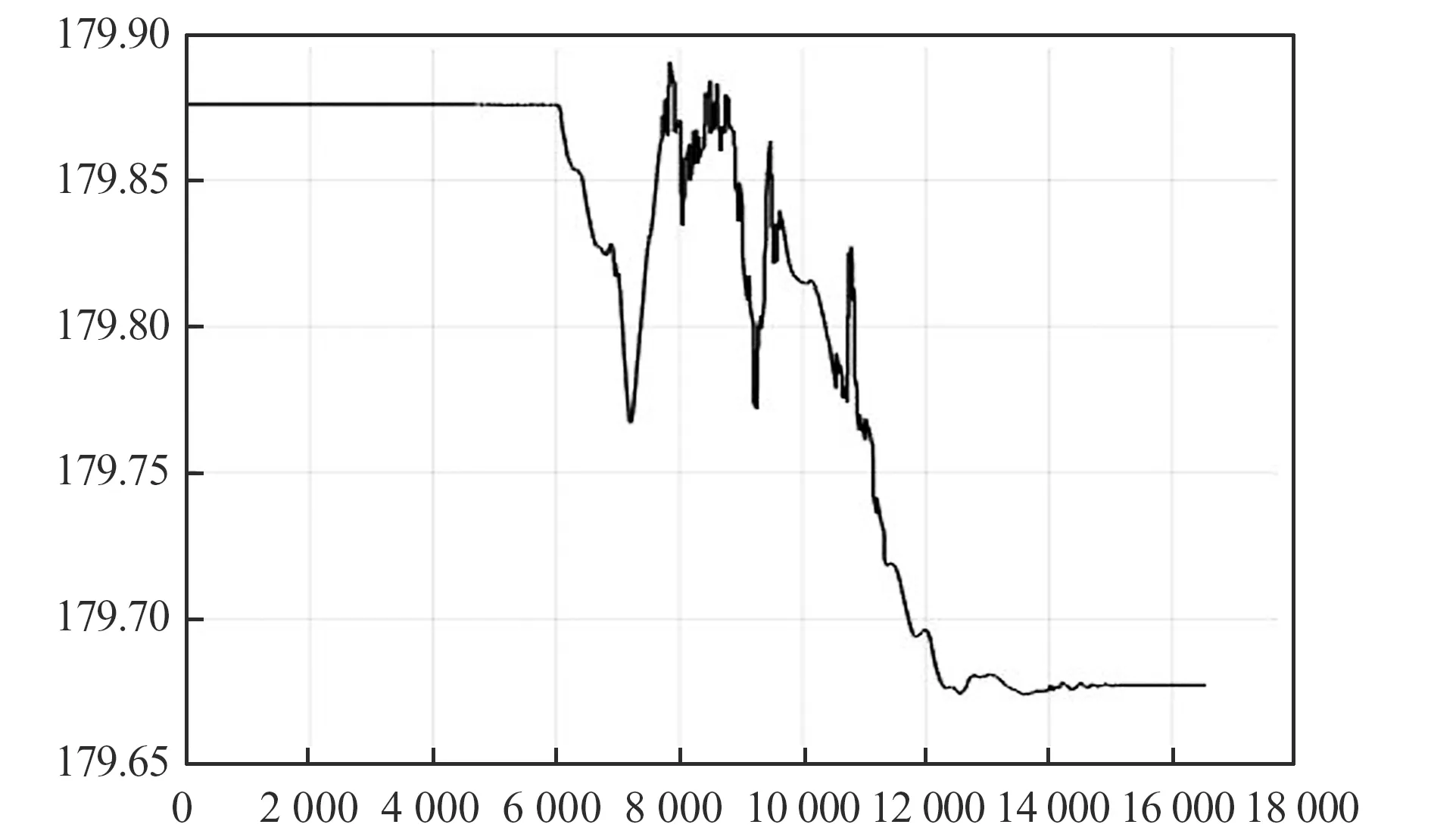
图11 车辆航向角

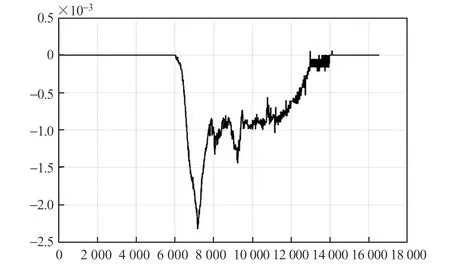
图12 行车方向前进速度

4.3 工况三：原地转向模式

原地转向模式主要用于车辆小范围内转向调头作业，整个过程中车身绕车辆中心点旋转运动，整个指令主要完成模式切换和转向运动，旋转角度以及旋转方向和单独设置，最大横向移动速度0.5 m/s，变道宽度4 m，转向速度控制采用与上述行走控制相同的控制方式。由图13～图16可以看出，在当前运行速度下，整个行车过程中车辆航向角变化平稳，停车时角度方向偏差较小，但是经过一次完整转向运动后，车辆中线点坐标偏离原来位置较大。主要原因为：①前后车桥机械安装不一致以及转向零位容易发生变化；②整个运行过程中由于很少或几乎没有探测到磁钉，无位姿矫正环节，连续转向中纯粹运动学估计带来了一定位置偏差。

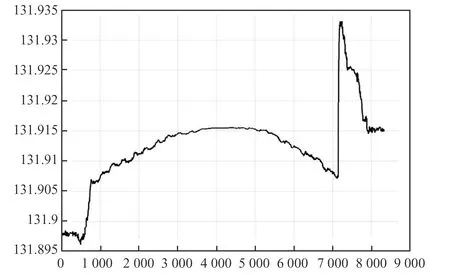
图13 车辆中心点横坐标X

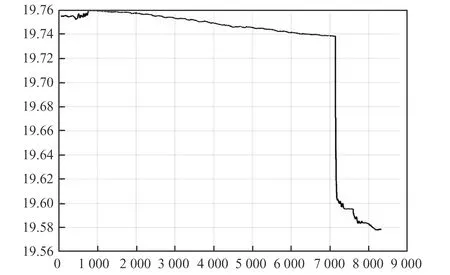
图14 车辆中心点横坐标Y

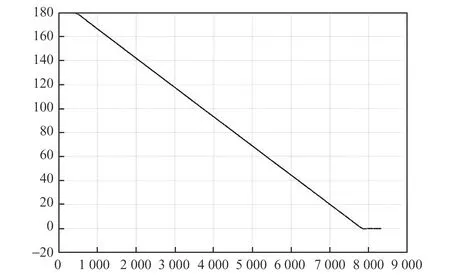
图15 车辆航向角

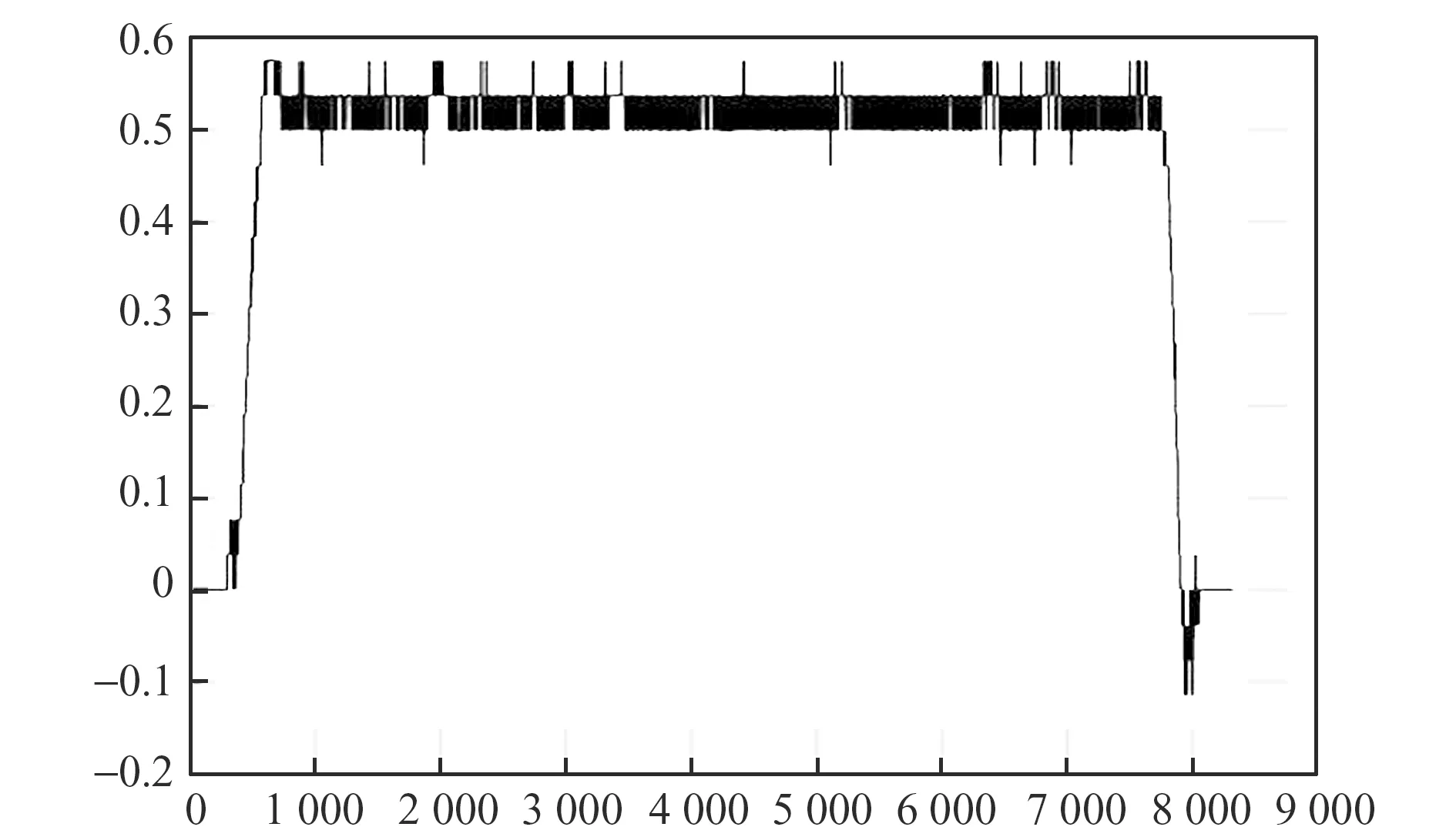
图16 后左轮速反馈值

5 结语

试验证明，车辆在各常见运行模式下的速度及转向角度跟踪控制效果良好，整个运行过程车辆运行平稳，前后控制点横向路径偏差较小，停车时位姿偏差较小，满足码头实际作业要求。但考虑到车辆前后车桥机械安装以及转向零位差异，原地转向效果还有待提高。基于车辆转向运动学的实时纠偏控制方法可作为后续优化的主要方向。