基于CEEMDAN-NAR-ARIMA组合模型的桥梁结构健康监测应变预测

朱利明， 卓静超， 邢世玲

(南京工业大学交通运输工程学院，南京 210000)

桥梁结构健康监测(structural health monitoring,SHM)系统近年来已经成为了特大桥、大桥，甚至中小桥必不可少的一部分。SHM系统采集了大量监测数据，而对这些数据的分析预测是对后续结构评估和安全预警的重要一步。

桥梁SHM的监测数据是以时间序列的形式存在的，因此对监测数据的分析预测即对时间序列进行分析。唐浩等[1]对西安白蛇峪大桥SHM系统的应变监测数据建立了自回归滑动平均(autoregressive moving average，ARMA)模型，预测误差基本小于10%，具有很好的预测效果。曾发明等[2]采用了乘积季节求和自回归移动平均(autoregressive integrated moving average，ARIMA)模型用准确地预测了桥梁拱座位移。在桥梁SHM领域，监测数据时间序列法分析预测大都还停留在经典时间序列分析理论的应用上，且多采用单一预测模型。由于外部或传感器自身的原因难免会产生很强的非平稳随机波动，并且存在模态混叠，此时采用经典时间序列分析理论进行分析预测就会产生比较大的误差。带自适应噪声的完全集成经验模态分解 (complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN)是目前最新的一种经验模态分解方法[3],可以自适应地按照不同频带将信号进行分解，非常适用于非平稳信号的分析处理。CEEMDAN方法由经验模态分解 (empirical mode decomposition,EMD)[4]、集成经验模态分解 (ensemble empirical mode decomposition,EEMD)[5]和互补集成经验模态分解 (complementary ensemble empirical mode decomposition,CEEMD)[6]发展而来，有效解决了模态混叠的问题并减小了重构误差，节约了计算时间。

针对经典时间序列分析理论在桥梁SHM监测数据分析预测上的不足，提出了一种基于CEEMDAN-NAR-ARIMA的组合预测模型，并通过上海市某斜拉桥SHM实测应变监测数据进行了验证。

1 预测理论分析

1.1 CEEMDAN信号分解方法

CEEMDAN是EMD方法的最新研究进展，其具体算法如下：

对原始信号x(t)添加服从标准正态分布的白噪声β0w(t)(i)，i=1,2,…,I，I为试验次数。

(1)对每一个x(t)(i)=x(t)+β0w(t)(i)，i=1,2,…,I都进行EMD分解，得到第一模态分量函数imf1及余量r1：

(1)

r1=x(t)-imf1

(2)

式(1)中，E为EMD分解运算符。

(2)对余量r1添加白噪声β1E1[w(t)(i)]形成新信号，再进行EMD分解得到新信号的第一模态分量函数作为原信号的第二模态分量函数imf2：

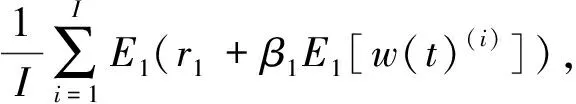
i=1,2,…,I

(3)

(3)对于k=2,3,…,K，计算第k个余量：

rk=rk-1-imfk

(4)

(4)在每一个阶段都加入白噪声形成一个新信号，并计算该信号的第一模态分量作为原信号新的模态分量，则第k阶模态分量函数：

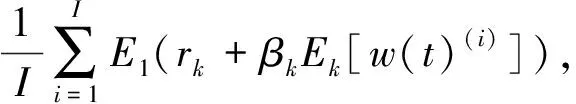
i=1,2,…,I

(5)

(5)重复(3)、(4)，直到余量不能被EMD进一步分解，或满足IMF条件或少于三个局部极值，此时即找出了所有的imf分量。

将所有分量进行重构得到原始信号：

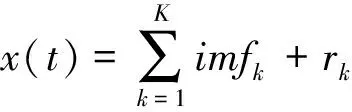
(6)

CEEMDAN在计算过程中，允许在每一个分解阶段添加的白噪声中选择合适的信噪比(signal-noise ratio，SNR)，所以计算过程是自适应的。

1.2 排列熵算法

通过信号分解有可能得到大量的信号时间序列分量，这些分量的实际意义通常很难进行判别。为了解决这一问题，引入了Bandt等[7]提出的一种算法—排列熵 (permutation entropy，PE)算法。PE算法可以很好地反映一个一维时间序列的复杂程度，具有计算简单、抗干扰能力强、对时间序列变化敏感、分辨率高的优点[8]。

PE算法的总体思路是计算时间序列的平均熵参数，熵值越大，时间序列的随机性越强；反之，时间序列越规则。其算法的计算步骤如下：

(1)对一个一维时间序列{x(t),t=1,2,…,n}进行相空间重构，得到重构矩阵：

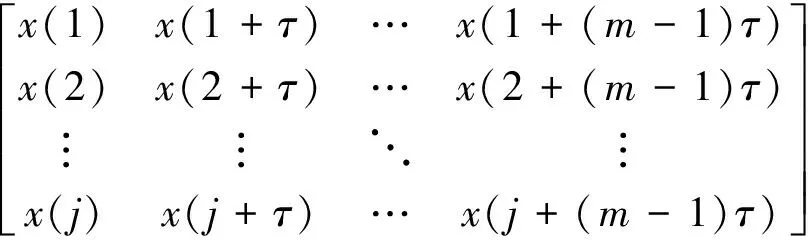
(7)

式(7)中，j=1,2,…,n-(m-1)τ;τ为延迟时间;m为重构维数。

(2)重构的行向量Yj=[x(j),x(j+τ),…,x(j+(m-1)τ)],j1,j2,…,jm为各个元素所在列的索引，将其元素根据数值的大小按照升序进行重新排序，如相邻元素数值相等，则按照索引的前后顺序进行排列，重构矩阵的每组行向量均可以得到一组符号序列S(r)=(j1,j2,…,jm)，r=1,2,…,l。显然符号序列S(r)排列数量l至多有m!种。

(3)计算每种符号序列S(r)出现的概率P1,P2,…,Pl，用Shannon熵的形式定义时间序列的排列熵Hp(m)为

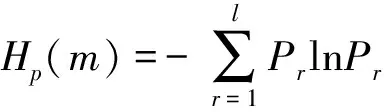
(8)

(4)为了方便，通常将排列熵Hp(m)进行归一化。从式(8)可以得出，当Pr=1/m!时，Hp(m)有最大值ln(m!)，因此对Hp(m)进行归一化：

(9)

归一化排列熵Hp显然在[0,1]范围内，Hp反映了时间序列的复杂程度，其值越小说明时间序列越规则，反之则越随机。将信号分解产生的大量信号时间序列分量利用PE算法计算出各个分量的熵值，可以定量判断各个分量的随机性程度，并以此为依据对各个分量进行分类，合并同类型的分量，来达到减少信号分量提高计算效率的目的。

1.3 ARIMA预测模型

ARIMA预测模型是时间序列分析最为经典的理论，可以对非平稳时间序列进行预测。ARIMA(p,d,q)表现形式为

Φ(B)dxt=Θ(B)εt

(10)

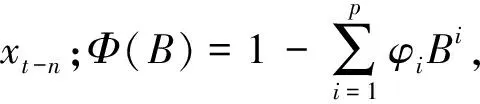
ARIMA预测模型的一般步骤为：时间序列的平稳性和纯随机性检验，模型识别，参数估计，模型检验和数据预测。其具体过程详见文献[9]。

图2 基于CEEMDAN-NAR-ARIMA组合模型预测流程Fig.2 Prediction flow based on CEEMDAN- NAR-ARIMA combination model

1.4 NAR动态神经网络模型

非线性自回归(nonlinear auto regressive，NAR)神经网络模型是一种用于分析时间序列的动态神经网络模型。之所以称之为动态神经网络是相较于静态神经网络而言的。一个神经网络包含输入层、中间层和输出层，如果在传递过程中信息只是单向的从输入层传递到输出层，中间信息没有任何反馈，则该网络是静态的，比如常见的BP神经网络；如果在传递过程中，输出信息作为输入信息反馈到上一层中，则该网络是动态的。动态神经网络的这一性质，在时间系列分析中非常的适用。NAR动态神经网络本质上就是静态神经网络结合输出反馈，其网络结构如图1所示。

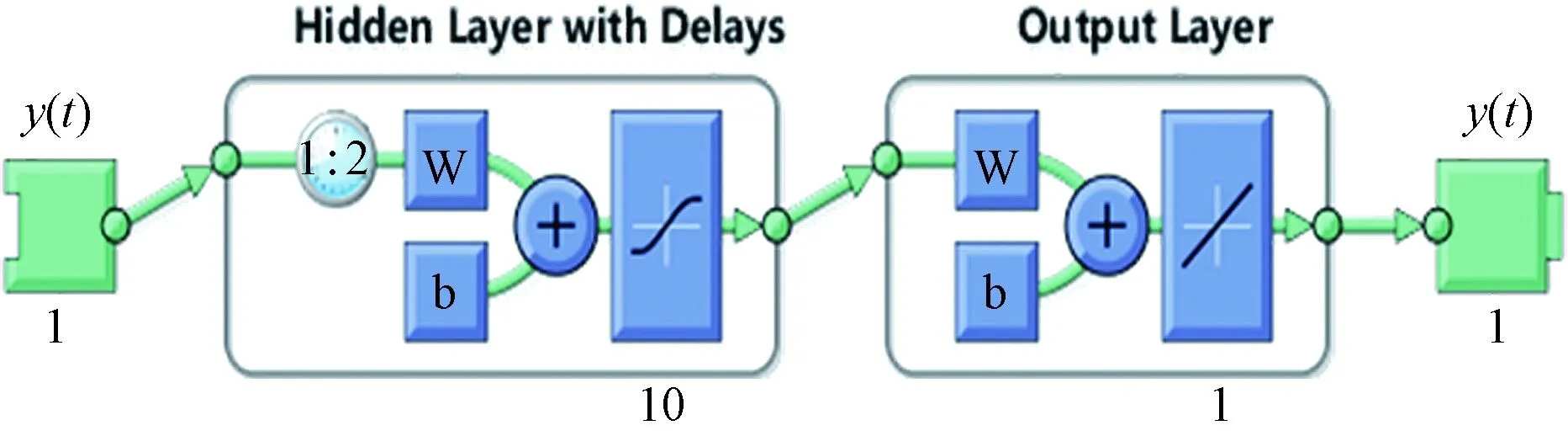
图1 NAR动态神经网络结构及工作流程Fig.1 NAR dynamic neural network structure and workflow

从图1可以看出，NAR动态神经网络由输入层(input layer)、隐含滞后层(hidden layer with delays)、输出层(output layer)构成，W为连接权值，b为阈值，这一过程可以表述为

y(t)=f[y(t-1),y(t-2),…,y(t-l)]

(11)

式(11)中，l为滞后阶数。从式(11)中可以看出，NAR动态神经网络是一个自回归过程，输出值取决于以往的值，而输入值为前一次的输出值。

2 组合模型的构建

综合上述的理论，将SHM监测数据利用信号分析方法进行分解与处理，然后用不同的模型对分解的信号进行预测，最后将预测值叠加，得到组合模型的预测值。提出的基于CEEMDAN-NAR-ARIMA组合模型的应变监测数据分析预测流程如图2所示。

3 工程实例

本案例选取了上海市某斜拉桥2017年7月1～5日的跨中腹板应变健康监测数据样本，共720期数据，每期间隔10 min。采用这些数据样本进行应变监测数据的预测并验证提出的组合模型的适用性。图3为某斜拉桥跨中应变监测数据时序图。

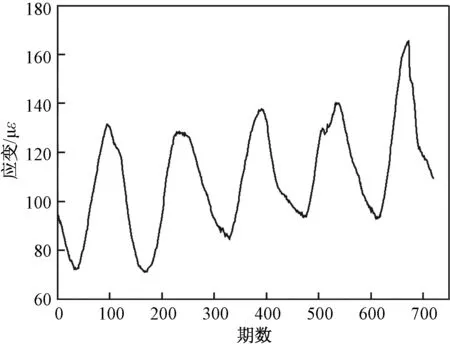
图3 应变时序图Fig.3 Strain sequence diagram

3.1 CEEMDAN信号分解

将应变监测数据看作为信号数据采用CEEMDAN方法对应变时间序列进行分解。图4为分解的结果，得到7个imf分量和一个余量r，其按照频率从高到低进行排列，通过观察亦可发现其随机程度也是按照从高到低排列的。

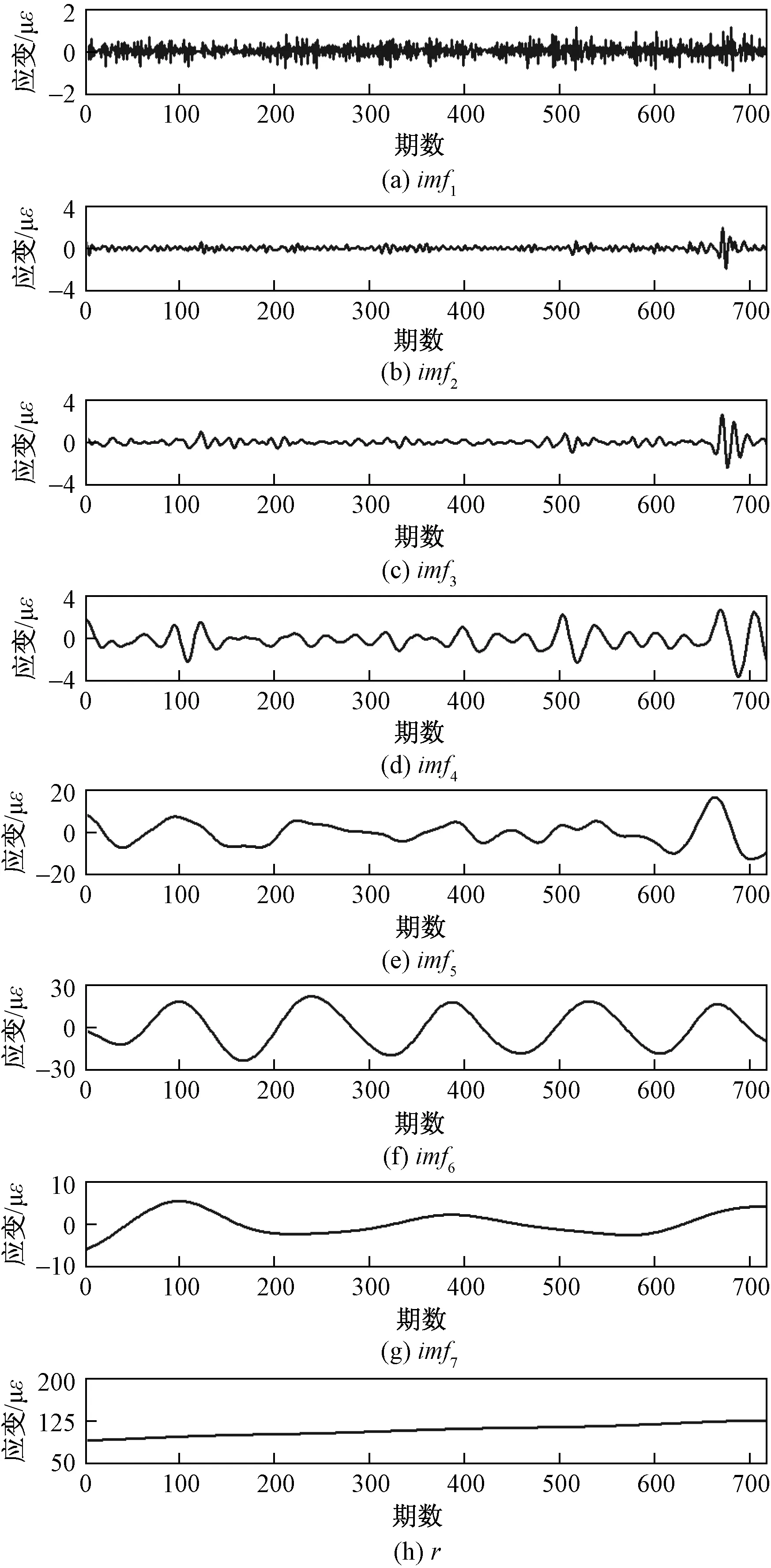
图4 应变数据CEEMDAN分解Fig.4 CEEMDAN decomposition of strain data

3.2 PE重组

经过CEEMDAN分解后得到的应变分量比较多，而且性质不够明显，只能够定性判断其随机程度的高低，直接进行数据预测会增加计算难度和降低预测准确性。因此，使用PE方法计算出各个分量的熵值，对其进行分类重组。

分别计算每一个分量的熵值。根据经验，PE计算参数重构维数m通常为3～7，延迟时间τ通常为1[10]。本例中，m=3，τ=1，PE计算结果如图5所示，各分量PE分别为0.995、0.863、0.692、0.535、0.463、0.430、0.408、0。

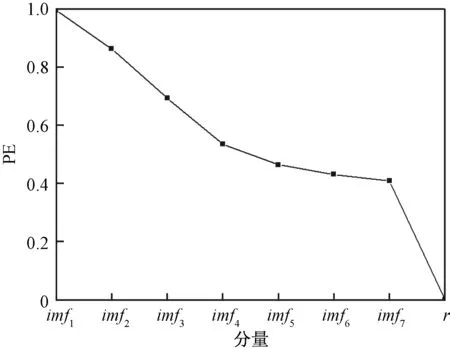
图5 各分量的PEFig.5 PE of each component

从图5可以看出，随着频率的减小，各分量的PE也逐渐减小，即随机程度越来越小。其中imf1分量随机程度最大，和imf2、imf3、imf4一同，PE呈现线性下降的趋势，因此，可以把这些分量归为一组进行合并重组为c1；从图5中可以看出imf5、imf6、imf7的PE呈现出一个较为平缓的平台，其随机程度较为类似，进行合并重组为c2；余量r的PE=0，从图4也能看出余量r为一组线性的序列，是十分平稳的序列，所以可以把余量r单独列为一组c3。进行PE重组后的情况如图6所示。

图6 经过PE重组后的新序列Fig.6 New sequence after PE recombination

从图6中可以看出，重组后的分量已从原来的8个分量减少到了3个分量，大大减少了计算分析的数量。并且根据桥梁SHM的工程经验，从图6中还可以推测出各个分量所代表的实际物理含义。分量c1代表了随机程度高的监测数据，可以近似地认为是车辆荷载、风荷载等一系列随机荷载的应变响应集合；分量c2有着明显的周期性，周期与日照一致，因此可以认为其代表日照变化导致的温度应变响应；而分量c3为线性的时间序列，显然可以认为其为季节性整体温度变化产生的温度应变响应。

3.3 组合模型预测

从图6中可以看出，分量c1的随机程度最强，分量c2呈现出比较明显的周期性，而分量c3则近似为线性。因此分别采用NAR动态神经网络模型、ARIMA模型和线性回归模型对分量c1、c2、c3进行50期长度的预测。

NAR动态神经网络建模参数如下：数据划分为70%训练数据、15%测试数据、15%验证数据；滞后阶数为7阶；隐含层神经元个数为13个；训练方法为Levenberg-Marquardt算法；训练次数为50次。ARIMA模型采用ARIMA(1,1,0)模型，自回归阶数p为1，差分次数d为1，移动平均阶数q为0。

基于CEEMDAN-NAR-ARIMA组合模型应变预测结果和实测值对比如图7所示。

为了验证基于CEEMDAN-NAR-ARIMA的组合模型的有效性，还同时分别建立了单一ARIMA模型、单一NAR模型和基于CEEMDAN的单一ARIMA模型对应变健康监测数据进行预测。4种模型的预测结果如图7所示。

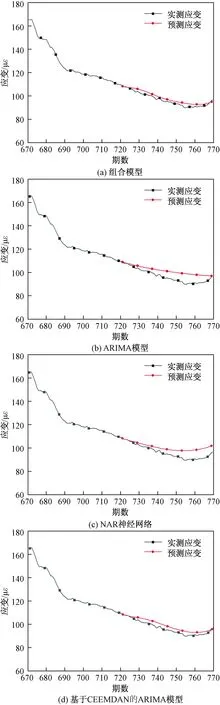
图7 各模型应变预测图Fig.7 Strain prediction of each model

3.4 预测结果分析

图8为4种预测模型的预测效果对比图。从中可以比较明显地看出，单一ARIMA模型、单一NAR模型的预测效果较差，经过CEEMDAN处理后的2个预测模型的预测效果较好，其中组合模型的预测效果最佳。

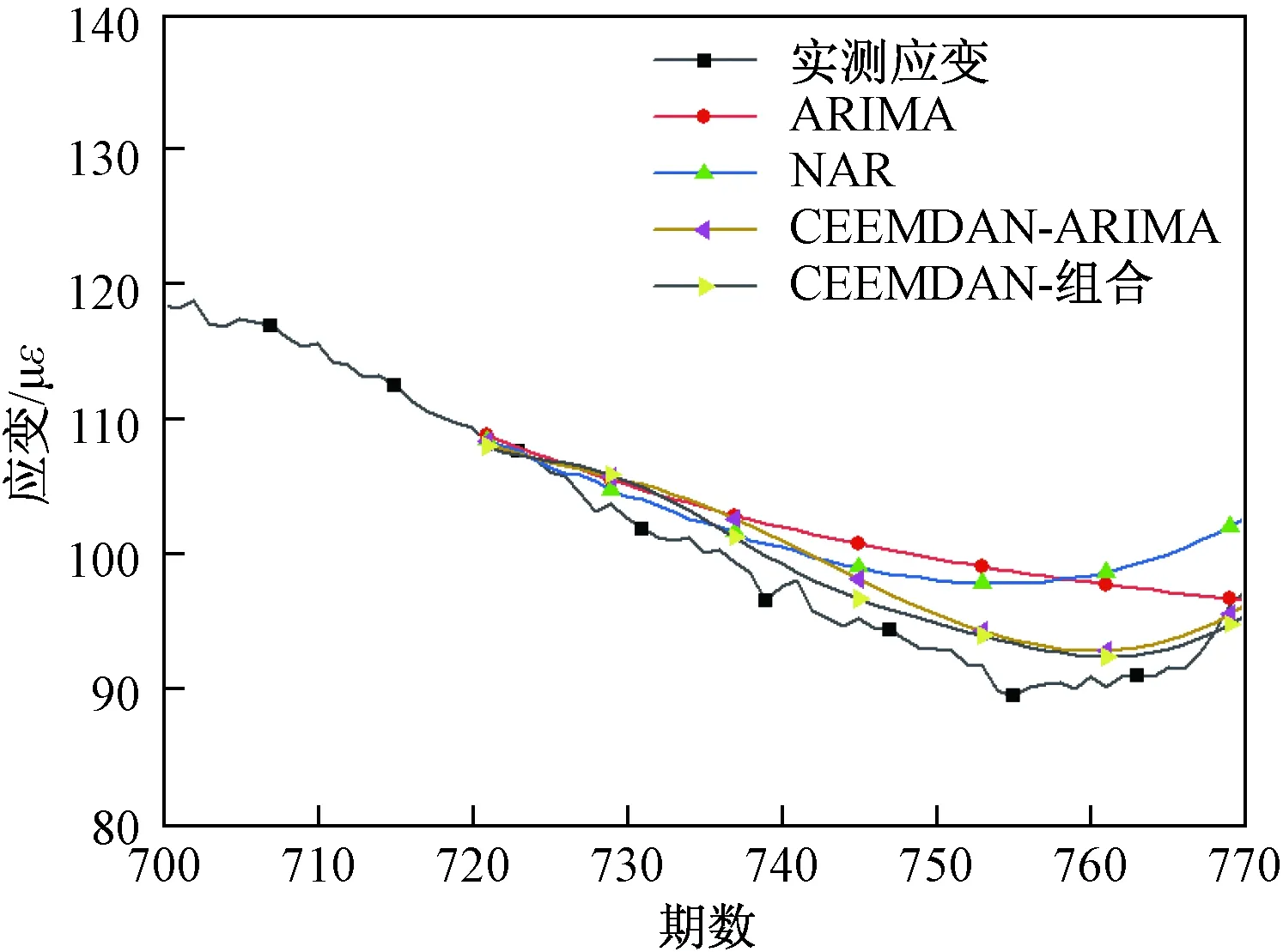
图8 4种预测模型应变预测图Fig.8 Strain prediction of 4 models

为了进一步定量的判断各个模型的预测效果，采用均方误差(mean square error，MSE)、平均绝对百分比误差(mean absolute percent error，MAPE)和可决系数(coefficient of determination，R2)三种统计学指标来评价模型的性能。MSE代表实测值与预测值点与点之间的误差，可以比较不同预测模型的稳定性，是应用最广的指标之一；MAPE不仅考虑预测值与真实值的误差，还考虑了误差与真实值之间的比例，是一个预测准确性的衡量指标；R2表示总离差平方和中可以由回归平方和解释的比例,代表回归效果的好坏。MSE、MAPE越小，R2越大，说明模型的预测性能越好。

表1为4种模型统计学指标的对比表。从表中可以看出，基于CEEMDAN-NAR-ARIMA的组合模型预测效果最好，基于CEEMDAN的单一ARIMA模型次之，而ARIMA模型、NAR模型性能最差，其R2统计指标为0.12左右，说明50期长度的预测是没有意义的。对比结果表明，在对桥梁SHM应变监测数据的预测中，经典的时间序列预测模型已经不能满足预测精度的要求，而组合模型能够更加精确地对非平稳的应变监测数据进行预测，具有明显的优势。

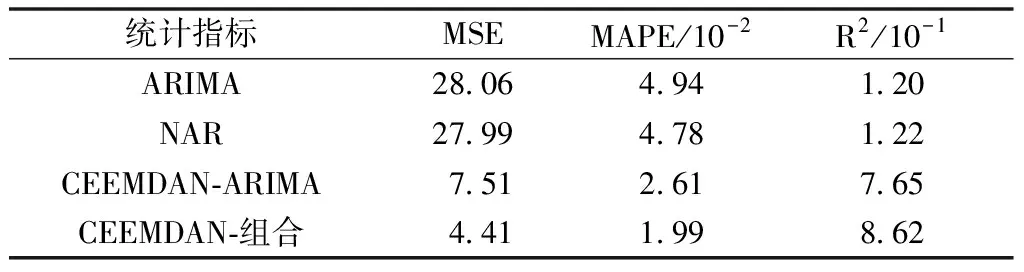
表1 6种预测模型的统计指标对比

4 结论

基于EMD方法的最新成果CEEMDAN方法，并结合NAR动态神经网络和经典时间序列分析理论的ARIMA模型组成组合了预测模型，应用于桥梁SHM应变监测数据的分析预测上，经过上海市某斜拉桥SHM系统实测应变数据验证，得到如下结论。

(1)CEEMDAN方法可以有效地分解出桥梁的随机荷载响应、周期性温度响应和整体升降温响应。

(2)通过PE算法可以有效地减少CEEMDAN方法分解出的imf分量，大大减小了计算量。

(3)将NAR动态神经网络与经典时间序列ARIMA预测模型进行组合，相比单一模型，有效地提高了预测模型的准确性。