基于花朵授粉算法的组合式风速预测
李 华, 任艺迪, 谷瑞政, 于 潇
(河北工业大学电气工程学院,省部共建电工装备可靠性与智能化国家重点实验室,河北省电磁场与电器可靠性重点实验室,天津 300130)
随着风力发电的大规模发展,风电场的数量迅速增多,风力发电比例持续上涨。但风力发电与天气状况密切相关,导致风速具有较强的波动性与间歇性,无法准确计算某一时刻的发电量,所以当大规模风电并网时,对电力系统的安全性和稳定性提出严峻挑战,严重限制了风力发电的发展。如果能有效地对风速进行预测,不仅可以为电网调度提供依据,还能有效地减少系统备用容量,安排风电机组的启停,从而降低电力系统的运行成本[1-2]。
目前,中外常用的风速预测方法主要为两类,分别为物理方法和统计方法。用物理方法进行预测一般会依据风速、风向、湿度和温度等气象信息并结合风电场周围环境等地理信息,通过计算得出最终的预测风速。如文献[3]中在数值天气预报(NWP)模型的基础上加入了卡尔曼滤波器,利用卡尔曼滤波器来修正NWP模型对风速与风力预测的最佳参数。此方法通常用作风电场的选址,且该方法计算量大,精度较差。统计方法一般不考虑风速产生的复杂过程,相对于物理方法过程较为简单,是近年来研究的热点。常用的统计方法为时间序列、人工神经网络、支持向量机等。文献[4]采用时间序列模型和人工神经网络模型对同一风电场进行了风速预测,实验结果表明,人工神经网络在短期风速预测方面要优于时间序列模型。文献[5]采用人工神经网络对印度山区进行风速预测,将风速、温度、气压、太阳辐射和海拔作为预测模型的输入,预测出日平均风速。文献[6]提出了一种混合智能算法优化最小二乘支持向量机(LSSVM)参数的方法,以提高脉动风速预测模型的性能。统计方法主要是通过提取输入的历史数据与输出之间的映射关系构建出预测模型,现选取BP(back propagation)神经网络为基础模型,并采用花朵授粉算法优化预测模型选取最佳参数以提高模型的预测性能和泛化能力。并针对风速数据的随机性和不稳定性从深度挖掘风速数据特性的角度出发,加入集合经验模态分解法,对风速数据进行处理降低其非平稳性, 以期进一步提高本文风速预测模型的精度。
1 集合经验模态分解
由于风能的间歇性、不可控性和随机性,风速数据一般具有较大幅度的波动。现主要利用EEMD(ensemble empirical mode decomposition)来深度挖掘风速序列的数据特性,降低风速数据的非平稳性提高预测的精度。集合经验模态分解法(EEMD)是在经验模态分解法(empirical mode decomposition,EMD)的基础上进行的一种改进。EMD是一种用来处理非线性、非平稳的自适应时频数据分析法[7]。EMD将原始信号逐级分解一系列不同特征尺度下的相对较平稳的本征模函数(IMF)。若任意一个信号的零点数和极点数的差值小于等于1并且由极大、极小值定义的上下两条包络线的均值为0,则称该信号为本征模函数。由于信号的间断性,经典的EMD在信号分解上存在一定的模态混叠现象,这一现象会使下文中建立的预测模型对IMFS的适应性下降[8]。为了改进模态混叠问题,提出了EEMD,在EMD的基础上添加了一组服从正态分布的高斯白噪声,有效改善了不同尺度下信号的混叠现象和信号的间断性,有效避免了EMD分解过程中造成的模态混叠现象[9]。EEMD具体实施步骤如下。
Step1在原始序列v(t)中加入噪声序列n(t),生成新的序列x(t)=v(t)+n(t)。
Step2找到x(t)中的极大值和极小值,采用三次样条插值函数拟合出上、下两条包络线即Imax(t)、Imax(t)。
Step3计算平均包络线m(t)=(Imin+Imax)/2,将加入噪声的新序列减去平均包络线构造新的差值序列y(t)=x(t)-m(t),判断y(t)是否满足本征模函数,若满足,则是一个本征模函数;若不满足,则作为一个新序列重复Step 1、 Step 2经过n次以后,所筛选出来的本征模函数称为IMF,记为h1(t)。
Step4对于原始序列x(t),减去IMF之后称为剩余分量r1(t),将r1(t)作为原始序列从第一步开始重复计算,可得到其余IMF分量,直到rk(t)为单调函数时停止。
2 花朵授粉算法
花朵授粉算法(flower pollination algorithm,FPA)是由Yang等[10]提出的一种新型启发式算法,该算法融合了蝙蝠算法和布谷鸟优化算法的优点,是一种非常有前途的算法。花朵植物已经进化了一亿年之久,在进化过程中,花植物繁衍过程中花朵授粉承担着举足轻重的作用。花朵授粉算法的实现是通过模拟自然界中的显花植物花朵传粉的过程,此算法结构简单、参数较少、无需梯度信息并易于实现。花朵授粉算法在实际应用中,一朵花对应优化问题中的一个解。根据植物种类的不同可分为自花授粉和异花授粉,自花授粉是指植物自身的花粉传播到自身的花朵上,在算法中将这种行为称为局部搜索过程;异花授粉是指异株、异花以及不同无性系之间的授粉,花粉通过传播者飞行很长的距离进行授粉,算法中将这种行为称为全局搜索过程。
假设FPA算法在理想条件下进行,假设如下:①生物的异花授粉为带花粉的传播者通过Levy飞行,达到全局授粉的效果;②自花授粉假设是局部授粉过程;③花的常性例如向阳性、向水性等可以被认为是繁衍概率,繁衍概率和所参与对比的两朵花的相似度成比例关系;④全局授粉和局部授粉之间的转换由转换概率p决定,由于受地理位置和风等其他因素的影响,局部授粉过程在整个授粉活动中是非常重要的部分[11-13]。基于上述阐述,花朵授粉算法的具体实现步骤如下。
Step1初始化FPA中的参数,如花朵种群数N,转换概率p,随机产生一个随机数rand∈(0,1)。
Step2计算每个解的适应度,并求解出当前的最优解和最优值。
Step3如果转换概率p>rand,按式(1)对解进行更新和越界处理。

(1)
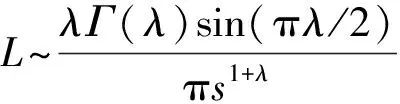
(2)
式(2)中:s≫s0>0,s为步长,s0为最小步长;λ=1.5;Γ(λ)是标准的Gamma函数。
Step4若转换概率p≤rand,按式(3)对解进行更新和越界处理。
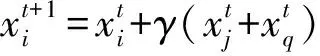
(3)

Step5计算由Step 3、 Step 4得出的新解的适应度,若新解的适应度最优,则用新解和新解的适应度代替当前解和当前解的适应度,反之则保留当前解和当前解的适应度。
Step6若新解对应的适应度的值比全局最优值优,则更新全局最优解和全局最优值。
Step7判断是否满足结束条件,若满足,则输出最优解和最优值;否则,从Step 3循环。
3 模型组合
3.1 花朵授粉算法优化BP神经网络

图1 组合模型预测流程Fig.1 Combination model prediction flow
BP神经网络是一种按误差逆传播算法训练的多层前馈网络。一般不少于3层,其网络拓扑结构由输入层、隐含层和输出层组成。使用这种算法时,无需提前知道输入与输出的映射关系,具有很强的自适应性和自组织能力。但BP神经网络存在收敛速度慢、不具有全局搜索能力和容易陷入局部极小值等问题[14-17]。FPA算法是一种新型的元启发式群智能算法,从该算法的优化原理上可以得知,该算法具有蝙蝠算法和布谷鸟算法的优点。具有良好的全局搜索性能。利用FPA算法优化BP神经网络可以大大减少陷入局部最优解的风险,提高全局搜索能力,鲁棒性强,在预测非线性的风速序列中有较大优势,预测精度较高。
FPA优化BP神经网络的基本思想:将FPA算法和BP神经网络的基于梯度下降的反向传播训练方法相结合,利用FPA算法对BP神经网络的权值和偏置进行优化。充分利用FPA的Levy飞行特性,进行全局搜索,将得到的一个初始的权值矩阵和偏置向量用于BP神经网络的训练,得到最终的神经网络结构。FPA-BP预测模型的基本流程如下。
Step1初始化BP神经网络,设置输入层、隐含层和输出层的节点数,网络权值和偏置。
Step2设置FPA算法的种群数N,变异因子的初始值和网络学习参数,并设置最大迭代次数或搜索精度作为网络训练结束的条件。
Step3BP神经网络的权值和阈值统一编码到个体花粉中,每个花粉个体代表一个BP神经网络结构。
Step4初始化所有花粉的速度和位置,计算各花粉的适应度函数值,并保留适应度值最小的个体。
Step5随机生成rand,计算转换概率p并进行全局搜索和局部搜索。并根据每个花粉的适应度函数值找出当前最优解。
Step6判断是否满足FPA结束条件,若满足,转Step7;若不满足,转Step 5。
Step7将最优值的花粉个体解码,作为BP神经网络的初始权值和初始阈值进行训练。
Step8判断是否满足BP网络训练结束的条件,若满足,则训练结束,得到最优的网络结构,可输入样本数据进行预测;若不满足,转Step 7。
3.2 组合模型实现
将获得的风速数据首先进行EEMD分解,把原本非线性、非平稳的复杂风速数据,分解为多个较简单的序列。将分解好的序列利用FPA-BP模型进行预测,并将结果组合得到预测结果。组合模型的基本预测流程如图1所示。
4 仿真分析
风速数据来源于西班牙加利西亚sotavento风电场。采用2018年3月1日—13日的风速数据作为样本,风速数据的采样间隔为10 min,风速数据如图2所示。对所有原始风速数据进行统计分析,如表1所示。
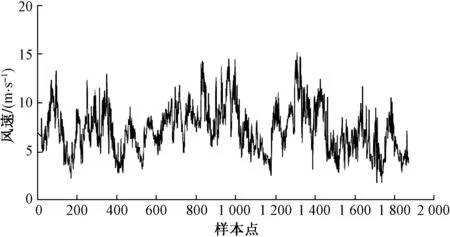
图2 风速数据Fig.2 Wind speed data

表1 风速数据统计Table 1 Wind speed data statistics m·s-1
由表1可以看出原始的风速序列具有较大的随机性和波动性。该风速序列通过EEMD分解为不同特征尺度下的相对较为平稳的若干序列,以便提高后续模型预测的准确性。经过EEMD分解后的风速序列如图3所示。
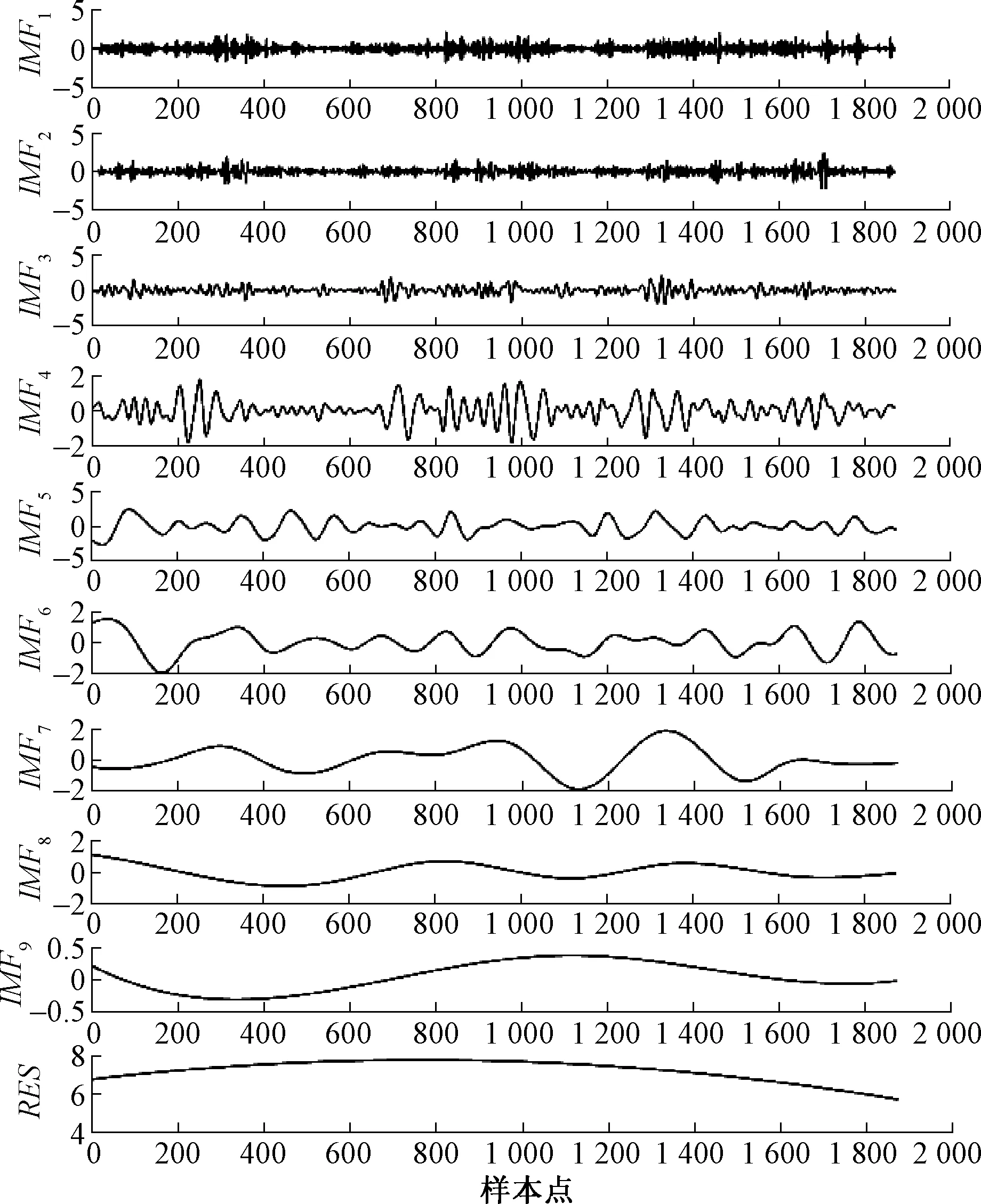
图3 经EEMD分解后的风速序列Fig.3 Wind speed sequence decomposed by EEMD
通过图3的分解结果可以看出,各个分量的频率依次由高到低,高频分量的波动性大是风速的随机影响部分;低频分量具有正弦波的特点,一般认为是风速的周期性分量;RES代表趋势分量,可以看出风速长期的变化趋势。
选取用样本数据中3月—13日12: 00共1 800个数据用于训练模型,3月13日从12: 10开始的12 h的72个数据点用于测试。根据上述的预测流程,输入FPA-BP模型进行预测,为了进一步探讨本文预测模型的性能,采用如下四种模型进行对比研究。第一种模型按照本文介绍的预测流程进行预测,称为EEMD-FPA-BP模型;第二种模型为先对原始风速序列进行EMD分解,再输入FPA-BP模型进行预测,称为EMD-FPA-BP模型;第三种模型对原始风速序列不进行处理,直接输入FPA-BP模型进行预测,称为FPA-BP模型。第四种模型为BP神经网络模型。图4为3月13日四种模型预测风速与实际风速对比结果。为了可以更加客观地评价这四种模型的性能,采用目前中外广泛使用的两个评价指标:平均绝对误差MAE和均方根误差(RMSE),定义分别为
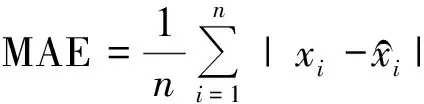
(4)
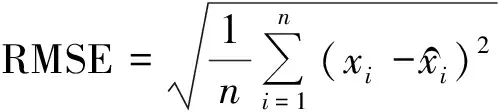
(5)
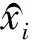

图4 3月13日风速预测Fig.4 Wind speed prediction on March 13
为了进一步验证本文提出的预测模型的泛化能力,同样分别选取了2月与4月的风速数据,对2月13日与4月13日12h的风速进行预测。图5为2月13日风速预测图。图6为4月13日风速预测图。各个模型的预测指标对比结果如表2所示。
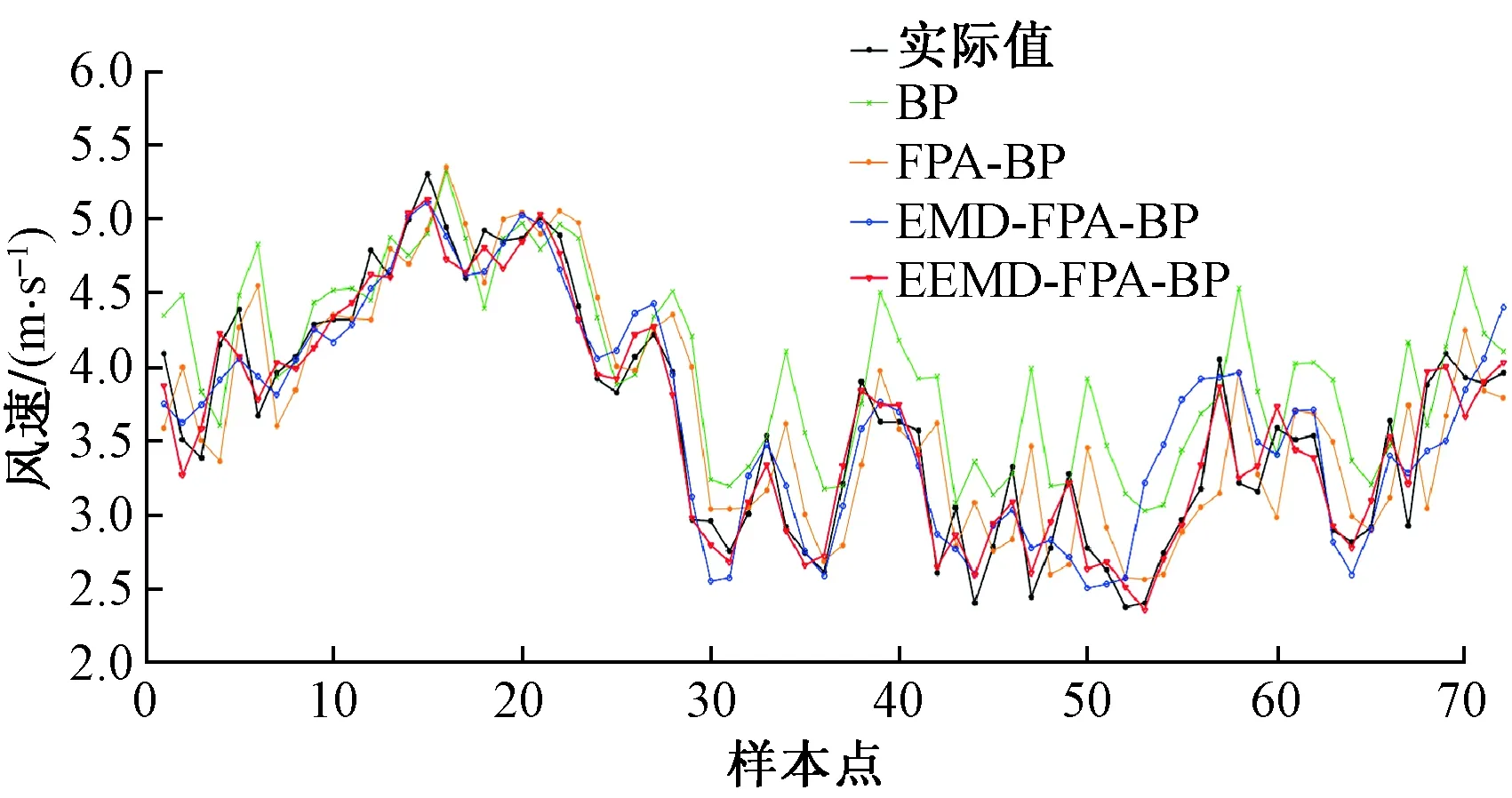
图5 2月13日风速预测Fig.5 Wind speed prediction on February 13

图6 4月13日风速预测Fig.6 Wind speed prediction on April 13

表2 模型误差分析Table 2 Model error analysis
从图5可以看出,2月风速数据较平稳,预测精度大大提高,可以看出风速序列的不稳定性是影响风速序列预测准确性的最大因素;由于风速序列具有一定的波动性与随机性,直接利用FPA-BP模型所预测的变化趋势往往滞后实际变化趋势,具有一定的滞后性。EMD-FPA-BP模型与EEMD-FPA-BP模型预测的风速序列与实际风速变化趋势大致相同,无滞后现象,说明基于数据分解的EEMD-FPA-BP模型与EMD-FPA-BP模型可以有效降低风速序列的非平稳性,提高预测精度。由表2的评价指标对比来看,FPA算法对BP神经网络的优化可以提高BP神经网络模型的预测精度,从三次预测结果可以得出,FPA-BP模型较BP模型的平均绝对误差降低了0.29 m·s-1,均方根误差降低了0.23 m·s-1。所提出的前三种模型的平均绝对误差均在0.5 m·s-1以内,均方根误差在0.8 m·s-1以内;所提出的EMD-FPA-BP模型在三次预测中两种误差的平均值为0.28、0.39 m·s-1,EEMD-FPA-BP模型在三次预测中两种误差的平均值为0.18、0.24 m·s-1,预测精度明显提高且较为良好稳定。主要是因为EEMD在EMD的基础上添加了一组服从正态分布的高斯白噪声,有效改善了不同尺度下信号的混叠现象和信号的间断性,有效避免了EMD分解过程中造成的模态混叠现象。
5 结论
通过对比进行仿真实验的四个模型得出花朵授粉算法对BP神经网络参数的优化可以提高全局搜索能力,避免陷入局部最小值,使BP神经网络模型的预测性能进一步提升。通过对风速数据的预处理可以提高预测模型的预测精度,证明集合经验模态分解法确实可以降低风速序列的非平稳性,集合经验模态分解法比经验模态分解法分解的更为彻底,降低了模态混叠现象。所以针对非线性、非平稳数据,可以采用基于数据分解的组合式模型进行预测,深度挖掘风速数据的特性,可显著提高模型预测精度,具有广阔的应用前景。

