基于面积划分的轨迹相似性度量方法
吕一可,徐 凯,黄振强
(1.上海海事大学交通运输学院,上海201306;2.上海海事大学上海国际航运研究中心,上海200082;3.上海海事大学信息工程学院,上海201306)
0 引言
随着大数据时代的来临,时空轨迹数据挖掘在越来越多的场景中被运用,包括动物的迁徙、行人的流线、运输载具行驶的轨迹,甚至是气象领域的气旋路径。这类的时空轨迹数据蕴含着大量的信息,而相关领域的分析研究也就显得尤为重要。在时空轨迹数据中,轨迹的相似性度量作为轨迹挖掘工作的关键步骤,在轨迹聚类、轨迹修复和预测等工作中起着重要作用。
时空轨迹的相似性对于移动对象分析来说是一个重要的指标,而这些工作大多面临着庞大而杂乱的数据,轨迹相似度量为相关数据的挖掘工作提供了保障。但对于不同的应用场景和实际需求,涌现出了一系列不同的相似度量方法,而各种轨迹相似度量方法对于轨迹相似及其程度有着各自不同的划定。
本文提出一种基于面积划分的空间轨迹相似的全局匹配度量的三角分割(Triangle Division,TD)方法,该方法适用于无路网结构轨迹,有着高效且在轨迹点缺失下有着更佳的鲁棒性的特点。本文的主要工作如下:
1)对面积划分的轨迹度量方法明确了相似属性的定义:两条轨迹间拥有着类似的运行趋势、位置与形状,且在非关键轨迹点数量缺失或者分布不均匀等特殊情况下仍然可判断轨迹相似。这一充要条件是很多轨迹相似方法中所未提及且容易遗漏的,而在实际应用中有着重要意义。
2)不同于基于轨迹点或段的度量方法,采用了面积划分的全新思路来度量轨迹的相似度。相较于传统根据轨迹点的相似度量算法,该方法将时间复杂度从T(n)=Ο(n×m)降低到了T(n)=Ο(n+m),且对于轨迹中非关键轨迹点缺失的情形有着更佳的鲁棒性。
3)提出了TD 的轨迹相似度量方法,建立了三角形面积分割规则,以计算轨迹间的面积。通过设置“指针”,有规则地将两条轨迹间的面积分割成若干不重叠三角形,并累加这些三角形的面积获得轨迹面积。再由此面积得到单位长度的轨迹间面积定义为轨迹距离,可与设定的阈值对比来确认此两条轨迹的相似性。
4)与传统方法提出的轨迹距离不同,本文方法是基于轨迹长度的相似度,使轨迹相似程度与轨迹的长度挂钩。该数值越大表明轨迹越相似,同时可设置对应于轨迹长度阈值的轨迹相似度下限。引入轨迹长度来得到轨迹相似度,而不是使用传统的轨迹点,该数值越大表明轨迹越相似。通过相似度,可设置对应于不同应用场景下的轨迹相似度下限来判断轨迹是否相似。
1 相关工作
轨迹相似度量的方法在实际的运用中,不同的相似性度量方法会对后续的轨迹挖掘工作产生较大的影响。因此,要具体根据所应用场景特点来选择合适的度量方法。
对于时空轨迹的相似度量方法,由度量对象的不同可分为基于轨迹点的相似度量方法和基于轨迹段的相似度量方法[1]。而对于轨迹点的度量方法,又可分为轨迹的全局匹配方法和局部匹配方法。
1)基于轨迹点的轨迹相似度量的全局匹配方法。欧氏距离(Euclid)[2]是较早提出的对于空间轨迹相似度量的方法,通过两条轨迹的轨迹点距离的累加来作为度量值。针对欧氏距离的不足,动态时间扭曲(Dynamic Time Warping,DTW)法[3]应运而生,该方法能将轨迹进行压缩,以找到两条轨迹间的最小距离。Chen 等[4]又提出了基于代价的编辑距离(Edit Distance on Real Penalty,ERP)的度量方法通过确定惩罚值来度量轨迹相似。而后刘坤等[5]对基于编辑距离的轨迹相似度量方法进行了运动物体的行为分析优化,使之更适用于空间移动轨迹。全局匹配的度量方法将空间轨迹整体考虑,以度量完整轨迹的相似性,此类方法对于轨迹点分布均匀轨迹有着较高的准确度,但缺点是时间复杂度过高。
2)基于轨迹点的轨迹相似度量的局部匹配方法。最长公共子序列(Longest Common SubSequence,LCSS)[6]是最早提出的轨迹相似度量方法,累加轨迹点间的判断值以度量相似。Chen 等[7]根据编辑距离又提出了实序列编辑距离(Edit Distance on Real Sequence,EDR)关注不相似的轨迹点距离。k-最佳连接路径(k Best Connected Trajectories,k-BCT)法[8]通过建立一些关键轨迹点来获取经过这些关键轨迹点附近的轨迹,适用于如旅游之类的模糊轨迹应用场景。弗雷歇距离(Fréchet distance)度量方法[9],即狗绳距离,走完两条路径过程中所需要的最短狗绳长度。朱进等[10]提出了多重运动特征编辑距离方法,以加权编辑距离作为相似性度量。局部匹配虽然解决了全局匹配方法无法度量轨迹部分相似的问题,但带来了时间复杂度的进一步增加,而同样通过轨迹点判断相似的做法,对于轨迹点的分布也有了较高的要求。
3)基于轨迹段的轨迹相似度量方法。最小边界矩形(Minimum Bounding Rectangle,MBR)法[11]则利用规则将轨迹分段并简化,再进行相似判断。豪斯多夫(Hausdorff)距离法[12]将轨迹分段并将轨迹的三种属性纳入考虑。结构相似距离法[13-14]在此基础上进行了长轨迹片段划分。而后,王培等[15]基于Hausdorff 距离又提出一种基于单位时间平均值的时空轨迹相似性度量方法。单向距离(One Way Distance,OWD)方法[16]通过判断两条轨迹匹配的轨迹段的距离积分作为轨迹的相似性。王飞等[17]提出了一种面向相似查询的轨迹索 引 方 法 GeoSAX (Geohash Symbolic Aggregate approXimation),依据数据量的大小对空间动态划分后做相似度量工作;室内空间的轨迹相似性度量方法[18]有效地减小了序列误差。先对轨迹段进行压缩的方法也有着很好的效果[19],梯形带相似聚类算法[20]的做法也是先压缩轨迹,并以梯形作判定区域。基于轨迹点的度量方法因为需要考虑每个轨迹点间关系,有着较高的时间复杂度。而基于轨迹段的相似度量方法将度量工作聚焦在了轨迹段上,多适用于有路网轨迹情形,虽提升了度量效率,但却增加了轨迹划分或是压缩等流程,增加了轨迹分析的工作步骤。
由于基于轨迹点的各种相似性度量方法的应用场景和对相似性的定义不同,也伴随着不同的性能[21]。针对上述方法,对于无路网轨迹,基于轨迹点的相似度量有着较高的时间复杂度,并且对于度量的对象通常为符合条件的轨迹点数的占比,极大地影响了方法的可行性。而基于轨迹段的方法的应用场景为以轨迹段为主要单位的轨迹曲线,如汽车的行驶轨迹的有路网结构的轨迹线路,此类的行驶轨迹多有着固定的轨迹段轮廓。所以,轨迹段的相似度量方法既增加了对轨迹段的划分或是压缩等预处理步骤,又只对以段为单位的轨迹作出判断,针对无路网轨迹网络的相似度量工作无法匹配。
本文聚焦于针对点轨迹的无路网结构的相似度量方法,提出了全新的基于面积划分的时空轨迹度量方法,该方法既解决了此类方法时间复杂度高的问题,同时增加了在缺失部分非关键轨迹点或轨迹点分布不均匀时的鲁棒性,这一点在现有方法中很少被提及并研究。
2 基于面积划分的轨迹相似度量算法
2.1 TD方法
2.1.1 TD方法的思路
本文基于轨迹间面积划分原理,提出了针对无路网轨迹全新的空间轨迹相似度量方法,该方法通过对轨迹间的二维空间进行划分的方式,透过一定的规则,连接两条轨迹点的线段形成互不重叠的三角形区域并累计作轨迹面积。同时,确定单位轨迹长度的面积阈值,通过轨迹面积和该阈值的对比来确定两条轨迹是否相似。
TD 轨迹相似度量方法的原理如图1 所示。轨迹PA和轨迹PB两条轨迹间的部分,由虚线分割面积,形成S1~S8到的8个互不重叠的三角形,累加此8 个三角形的面积得到轨迹面积用以相似度量。
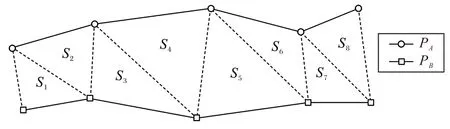
图1 面积划分示意图Fig.1 Schematic diagram of area division
2.1.2 TD方法的划分和累加规则
TD 方法通过构建规则分步确认三角形的三边,避免出现三角形面积重复累加。
划分和累加的循环思路如下:
步骤1 得到三角形边L1。连接a 与b 点得到三角形边L1。且在循环开始时,a与b分别为轨迹PA和PB的第一个点。
步骤2 确认三角形边L2。对比轨迹点a 与b+1 连线和轨迹点b 与a+1 连线的长度,即图中带箭头直线i 与j 的长度。并取较短者连接,得到此线段为L2。
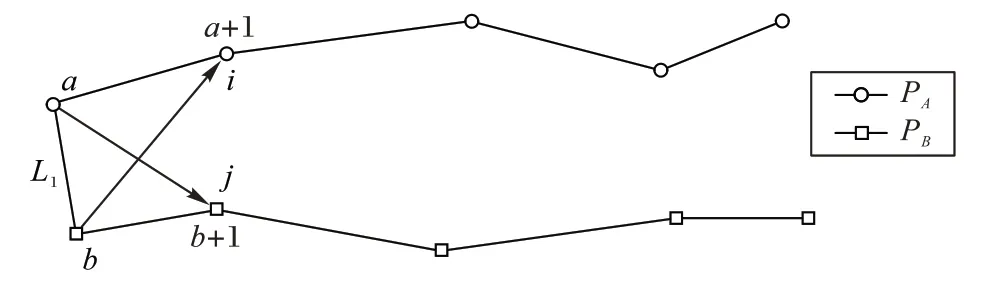
图2 “指针”法示意图一Fig.2 Schematic diagram 1 of“pointer”method
步骤3 得到L3和三角形面积的计算。由L1和L2确认的三角形,可以得到第三条边L3。计算该三角形面积,累加进轨迹间总面积sum。
步骤4 循环和终止。步骤2中连接较短直线后,对应的a 或b 将进入下一个轨迹点a+1 或b+1,并回到步骤1 继续计算。当a或b进入轨迹末点时,结束循环。

图3 “指针”法示意图二Fig.3 Schematic diagram 2 of“pointer”method
2.2 模型的构建
TD 方法使用的是轨迹间单位长度的面积作为轨迹距离。从两条轨迹的第一个点a1和b1开始,得到两条轨迹的面积SA(Sum Area)为:
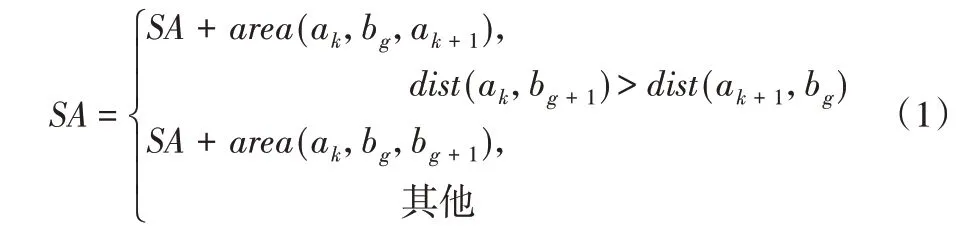
其中,area(ak,ag,ak+1)表示ak、bg和ak+1三点所围成三角形的面积。
得到两条轨迹的平均长度为:
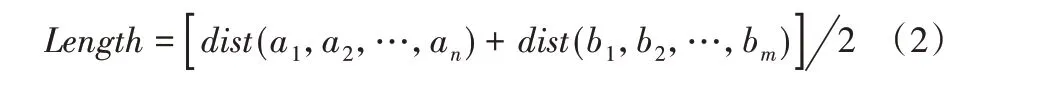
最后得到该方法下单位长度面积(Area Per Length,APL),即轨迹距离:

当使用APL 度量轨迹相似度时,需要设置轨迹距离的度量阈值γ,对比距离值是否超过阈值。
为了更好地与其他轨迹相似度量方法作对比,该方法引入了相似度(Similarity)的定义。同时,该相似度很好地去除了轨迹距离的单位,也能使不同长度范围的轨迹有着不同的度量敏感度,如长度量值大的轨迹间在轨迹距离相对较大的情况下也可判断它们为相似。相似度的计算公式为:
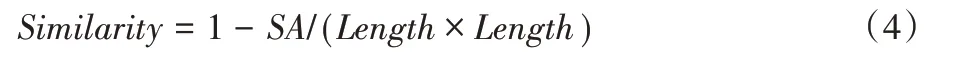
该相似度代表的是考虑轨迹总长的情况下考虑的轨迹相似程度,该数值越大表示轨迹越相似,而不同的应用场景和阈值设置下,应根据轨迹距离的阈值来设置相似度的阈值。
轨迹相似度量的TD方法的伪码描述如下:
算法 轨迹相似度量的TD方法。
输入 两 条 轨 迹 的 轨 迹 数 据PA={a1,a2,…,an}和PB={b1,b2,…,bm};轨迹间单位长度面积阈值γ;
输出 输出两条轨迹的单位长度面积APL 和相似度Similarity;输出两条轨迹的相似性,即是否相似。
1) for each ak∈PAdo //对点ak在轨迹集合PA中
2) if each akis the first point then
3) a ←0 //由元素a记录轨迹A的索引
4) b ←0; //由元素b记录轨迹B的索引
6) L1←distance(a,b) //计算a与b对应直线长度
7) L2_AtoB ←distance(a,b+1) //设置了“指针”
8) L2_BtoA ←distance(b,a+1) //设置了“指针”
9) if L2_AtoB ≤L2_BtoA then
10) L2←L2_AtoB //得到L2长度
11) b ←b+1 //元素b的索引进入B下一个点
12) L3←distance(b,b+1) //计算L3长度
13) SA ←SA+area(L1,L2,L3)//L1、L2和L3形成的三角形面积累加入sum
14) else //如果L2_AtoB更长
15) L2←L2_BtoA //使L2得到L2_BtoA的数值
16) a ←a+1 //元素a的索引进入轨迹A下一个点
17) L3←distance(a,a+1) //计算L3长度
18) SA ←SA+area(L1,L2,L3) //累加面积
20) if b is last point of the trajectory then
21) exit; //若b进入轨迹末端,则结束循环
23)end for
24)for each ak∈PAdo
25) L ←L+distance(a,a+1); //计算轨迹A的长度
26)end for
27)for each bk∈PBdo
28) L ←L+distance(a,a+1); //计算轨迹B的长度
29)end for
30)Length ←(LA+LB)/2 //计算长度平均值
31)APL ←SA/Length //计算轨迹间平均长度的面积
32)Similarity=1-SA/(Length×Length)
3 实验结果与对比
3.1 对照组设置
3.1.1 对照组的选择
本文选取了最具代表性的基于轨迹点的轨迹相似度量方法最长公共子序列(LCSS)方法和有着较高鲁棒性的弗雷歇距离(Fréchet distance)度量方法进行对比实验。
而由于基于轨迹段的相似判断方法主要针对有路网结构的轨迹使用,无法形成对比,所以在本节的实验中也不加以讨论。
定 义 两 条 轨 迹 点 集 合 为PA={a1,a2,…,an}和PB={b1,b2,…,bm},最长公共子序列方法的表达式为:

其中:LCSS(ak,bg)为轨迹PA在轨迹点ak和序列PB在轨迹点bg前的最大公共子序列长度;dist(ak,bg)为PA轨迹中的第ak个点与PB序列中第bg个点间的距离;γ 为设置的距离阈值。可以看出,该方法获取的是符合点间距离阈值的轨迹点数,用来衡量轨迹的相似。
弗雷歇距离度量方法表达式为:
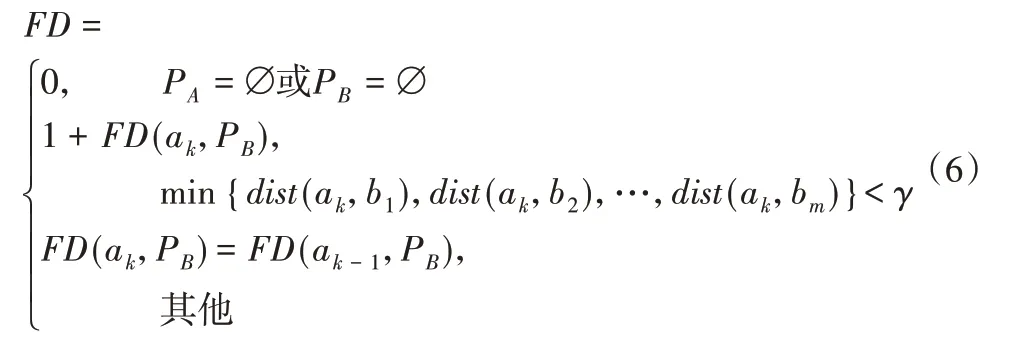
而弗雷歇距离度量方法将最长公共子序列方法中只关注点与点的距离转化成点与轨迹的距离,即dist(ak,bg)变为dist(ak,PB)从而增加了该算法的鲁棒性。
3.1.2 阈值与度量值
TD 方法中设置了单位长度面积为m km2的阈值;对应于两种基于轨迹点相似度量方法设置了m km 的轨迹点距离阈值,并使用了相似度来查看相似程度。
在对比实验中弗雷歇距离度量方法和最长公共子序列方法的度量值最大均为100%,表示相似度最高,度量值表达式为:

3.2 轨迹缺失下的敏感度
本节的实验对比数据使用了船舶轨迹应用场景下的AIS数据。选择了两条真实的船舶轨迹数据,PA轨迹有660 个轨迹点,PB轨迹有650 个轨迹点。同时,在分别随机删除200、300 和400 个轨迹点时的相似情况设置了20 个平行对照组取均值,所得到的各方法的相似度量如表1所示。
在表1和图4中可以发现,轨迹缺失后的度量值发生的变化。首先,LCSS 方法在轨迹点缺失后的度量值明显地降低了,在缺失后的相似度判断上有着明显的误差。而TD方法和Fréchet distance 度量方法在轨迹点随机缺失的情况下都有着很好的鲁棒性。
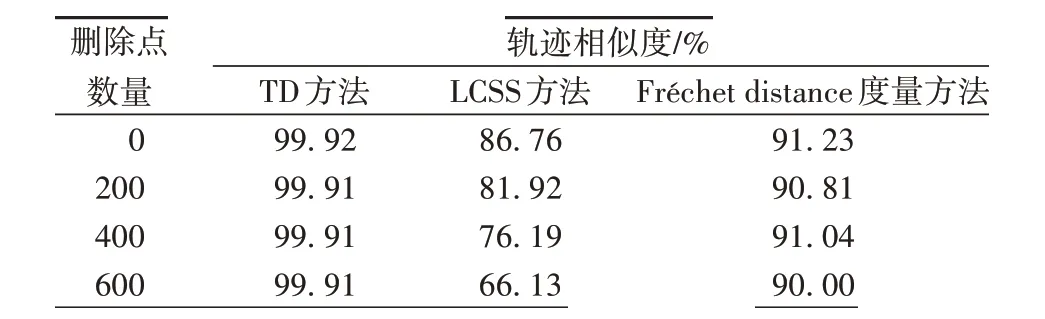
表1 轨迹点随机缺失的轨迹相似度量值Tab.1 Trajectory similarity measurement with randomly missing trajectory points
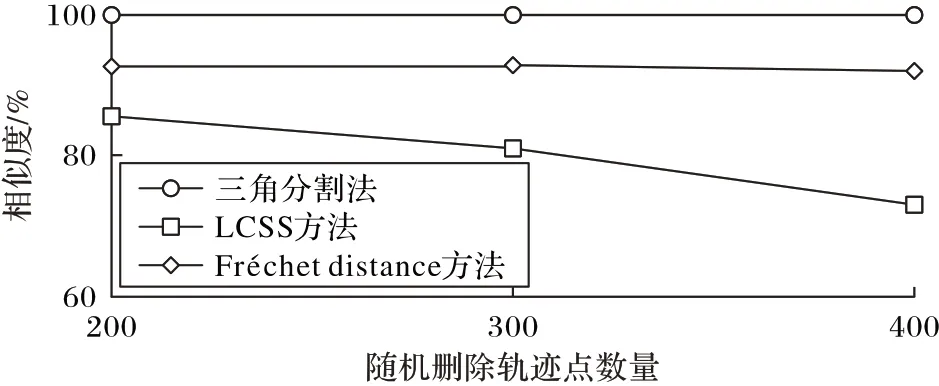
图4 轨迹点随机缺失的轨迹相似度量变化Fig.4 Trajectory similarity measurement change with random missing trajectory points
在表2 中,发现LCSS 和Fréchet distance 度量方法的耗时远大于轨迹划分的方法,且随着轨迹点数量的增加,时间复杂度T(n)=O(n×m)将呈指数级增长。而同样的轨迹点数量下,三角分割的轨迹相似度量方法则将时间复杂度大幅度减低。从表2 中可以看到,在此案例给出的轨迹中,TD 方法相对于两种轨迹点划分方法的耗时减小了接近90%。

表2 轨迹点随机缺失的轨迹相似度量耗时 单位:sTab.2 Trajectory similarity measurement time with randomly missing trajectory points unit:s
3.3 不同位置关系的空间轨迹相似判别
此节设置了4 种特殊的轨迹间关系进行对比,分边为绕圈、折返、轨迹相交、轨迹交叉且疏密不均的轨迹间关系。
4 种轨迹间关系代表了在各种轨迹应用场景下的特殊且不易判断相似的部分截取轨迹:绕圈是轨迹出现返回的圆周轨迹;折返是轨迹出现原路的折返;轨迹间相交是两条判断轨迹间的关系出现相交但仍然是相似轨迹的情况;轨迹间交叉且疏密不均是特殊的情况,指轨迹呈大角度交叉,完全不相似,但两个轨迹的轨迹点疏密分布非常地不均匀。
四种情况均采用了算法随机生成30 组数据,设置2 为轨迹距离阈值,如图5 为各种不同位置关系轨迹的一次随机生成数据绘制的图像。
对于相似度的判断,100%的相似度定义应指两条轨迹的完全重合。所以,由图5 可见,绕圈、折返和相交情况的两轨迹的相似度应趋近于100%,而不到达100%。而对于轨迹间交叉且疏密不均的相似情况,该截取段在如航空和海运中经常出现,这种相似情况下,相似度应较前三种情况低,但不应出现相似度过低的判断。
各方法下相似度的平均值如表3 所示。其中,TD 方法得到的结果包括相似度和轨迹距离。
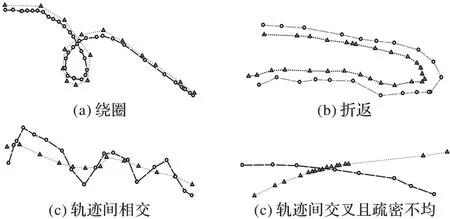
图5 不同轨迹间关系示例Fig.5 Example of relationship between different trajectories
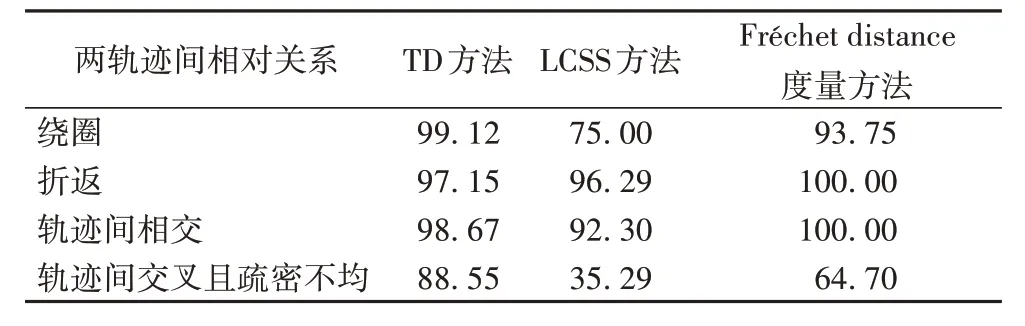
表3 不同轨迹间相对关系的相似度量值 单位:%Tab.3 Similarity measurement of relative relationship between different trajectories unit:%
由表3可知:
1)表中的前三种关系为两条空间轨迹相似,可以发现在出现复杂的轨迹间关系时,LCSS 方法在度量情况出现了误差,Fréchet distance 度量方法在绕圈轨迹情况下也出现了部分的段判断为不相似。
2)Fréchet distance 度量方法对于前三种情况是否相似的判断虽然准确,但在相似度数值的确定下同样体现了轨迹点判断方法的不足,该三种情况的度量值不应出现百分百的相似度。而第四种情况,该方法则出现了较大的误差,对于交叉却相似情况的轨迹,单纯依照轨迹点的判断使相似度在疏密不均下过低。所以,Fréchet distance 度量方法在后三种情况的判断上均差于TD方法。
3)轨迹交叉且轨迹点疏密不均匀的第四种情况暴露了基于轨迹点相似度量的通病,以轨迹点相似个数来度量轨迹相似度的可靠性在轨迹点疏密分布不均匀的情况下非常地不可靠。如64.70%的数据会产生两条轨迹有大部分轨迹段相似的误判,而这也非全局判断方法下的通病。而TD方法在此情况下依旧能够判断轨迹的相似情况。
3.4 实验结论
1)TD 方法的空间轨迹相似度量弥补了最大公共子序列方法对于轨迹缺失下判断误差的问题,同时也有着弗雷歇距离度量方法的鲁棒性。
2)TD 方法的空间轨迹相似度量方法相比基于轨迹点的相似度量方法有着极低的时间复杂度,使算法的执行速度得到了极大的提升。
3)对于复杂的轨迹运行情况下,不同的疏密情况对TD方法的空间轨迹相似度量方法影响很小,相比基于轨迹点的相似度量方法有着显著优势。这样的差异来源于度量方法的度量思路,基于轨迹点的度量方法对比每一个点的情况,再查看相似点所占比例来度量相似;而本文中提出的TD 方法,对单位长度的轨迹间面积设置阈值,是对轨迹间整体的考量。
4 结语
本文提出了TD 的轨迹相似度量方法用于空间轨迹相似度量,该方法有着相似度量准确、时间复杂度低的特点,在对船舶的AIS 数据进行不同情景下的实验中也取得了不错的效果,对比基于轨迹相似度量方法,发现该方法对于轨迹缺失和轨迹点分布不均匀下有着较好的鲁棒性。同时,不同于之前对于轨迹点和轨迹段的相似度量方法,本文提出的空间轨迹度量TD方法有着不错的适用性,也为轨迹相似度量方法提供了全新的思路,为进一步的轨迹挖掘工作打下了基础。在后续的工作中,可对时空轨迹的相似度量进行应用,增加时空维度来更加精确化度量以应用于更多的场景。

