基于HBase的多维索引查询机制的优化
徐江峰,谭玉龙
(郑州大学信息工程学院,郑州450001)
0 引言
随着无线和移动技术的进展,对移动性的需求日益增加,基于位置的服务(Location-Based Service,LBS)利用移动设备的能力,通过移动网络提供用户当前的地理位置。它们允许移动用户搜索他们的环境,并使他们能够立即访问个性化和本地化的内容。目前,移动用户可以使用各种各样的LBS,包括路由映射应用程序、交互式城市指南、位置感知营销、对象跟踪和监控,以及基于邻近[1]查找对象。LBS对底层支持平台提出了广泛的需求,包括对多维数据建模、处理数百万用户的高速更新以及对大量数据进行实时分析。
通过利用内置的索引功能和丰富的查询处理语言,传统关系数据库管理系统(Relational Database Management System,RDBMS)可以在多维数据上提供高效和快速的复杂查询处理。这些索引功能是通过在关系存储之上创建额外的索引层来提供的。例如,Oracle spatial 支持基于R-tree[2]和四叉树[3]的索引。然而,这些集中的系统会产生单一的故障点,实现起来成本很高,而且随着数据量和用户数量的增长,会遇到可伸缩性瓶颈。
分布式键值存储成为一种提供弹性数据管理服务的新范式,可以根据不同应用程序的需求进行伸缩。当前的键值存储(BigTable[4]、HBase[5]和Cassandra[6])被设计成高可用性、高容错性和保持高更新吞吐量支持数百万用户;但是,这些键值存储只能处理单个属性的高效精确匹配查询,因为它们缺乏访问多个属性的内置索引机制。对于查询多个属性,有两个设计选项可用:第一种选择是为每个属性创建单独的索引,但是,在管理大量数据时,创建多个索引表会给系统带来巨大的额外负载;第二种选择是使用MapReduce[7]范式的并行处理来扫描整个数据集,然而,LBS 需要实时的查询处理,因此,对整个数据集进行并行扫描并不是很有用。
本文提出了一种新的数据分布和多维索引框架New-grid来支持云平台上的LBS。由于键值存储的优点,使用它们作为存储后端是很自然的选择。然而,在键值存储之上开发这样的索引框架的关键挑战是:如何对多维数据进行有效建模,并为其提供高效处理复杂多维查询的能力。New-grid 采用基于Hilbert 曲线[8]的线性化技术解决前一个问题,然后将其与改进的覆盖网络P-Grid[9]进行集成。优化的New-grid 通过预先计算并将子空间分配给网络中的节点,成为一个静态网络。Hilbert 曲线在保持数据局部性的同时,将多维属性映射到一维。另一方面,P-Grid 以虚拟二进制形式呈现的节点进行排列,并将多维搜索空间划分为子空间。前缀结构充当底层键值存储之上的静态路由索引层,并充当多维搜索的入口点。因此,本文主要工作之一就是建立这个P-Grid覆盖网络,然后由New-grid 根据P-Grid 前缀的路由机制在集群中进行分布复杂的查询。综上所述,本文的主要工作如下:
1)提出一种新的数据分布和多维索引框架New-grid,它可以有效地索引和处理点、范围和K 最近邻(K-Nearest Neighbors,KNN)查询。
2)利用基于Hilbert 空间填充曲线的线性化技术将多维数据转换为一维数据,同时保持了数据的局部性。
3)提出一种利用改进的P-Grid 前缀路由机制动态处理线性化值上的点、范围和KNN 查询的算法,以消除创建和维护单独索引表的开销。
4)在Amazon EC2 上进行实验来测量insert 吞吐量以及点、范围和KNN 查询,以展示本文的框架相比MD-Hbase 的有效性。
1 相关技术
1.1 空间填充曲线的线性化
线性化是一种将多维属性映射到一维空间上的降维方法。空间填充曲线是一种线性化技术,它是在不重叠的情况下,通过访问n 维超立方体中的每个点来构造连续曲线。它们的优势是:在映射之后,在n 维空间中的相邻点在一维空间中也保持邻近。因此,空间填充曲线在图像处理[10]、科学计算[11]、地理信息系统[12]等需要顺序访问数据集的应用中得到了广泛的应用。在New-grid 中,本文使用Hilbert 空间填充曲线索引底层一维键值存储中的多维点,以提高查询效率。
Hilbert 曲线是一种连续的空间填充曲线,它在多维数据点上产生顺序排列。形式上,希尔伯特曲线是一个一对一的函数:

其中n 是2m×2m 空间维度的数量,n ≥2,m >1。这个函数决定了Hilbert 值(H 值)的原始坐标空间中的每个点的H值∈(0,2mn-1)。图1 展示了二维空间中的坐标及其一阶等效Hilbert 曲线。递归构造阶数i >1 曲线,将一阶曲线的每个顶点旋转或反射后,替换为i-1阶曲线,以适应新的曲线[13]。
递归构造过程也可以表示为一个树形结构(图3),用二进制符号[14]表示坐标点n 与H 值的对应关系。树的深度等于曲线的阶数,根节点对应图1 的一阶曲线。同时,任意树级的节点集合i 描述了i 阶曲线,以点(10,11)为例,用图3 所示的树结构来演示二维二阶H 值的计算。在第一步中,将点(10,11)坐标的顶端位串联起来,形成n点11。在根节点上,这个n点对应于子空间10。在下一步中,沿着根的子空间10,从树的第1 层下降到第2 层。把这个点坐标的后两位连起来形成n 点01。在树的第2 层,n 点对应于子空间01。由于没有更多的层可以下降,H 值的计算就结束了。点(10,11)的最终H 值由在每个步骤中从根节点开始的子空间的值串联而成,即1001。使用树结构生成点的H 值需要每个属性的基数相等。然而,在LBS 中,属性的基数可能是不相等的。因此,在Newgrid 中,使用文献[15]中给出的算法计算H 值,该算法使用逻辑运算高效地计算Hilbert 曲线上属性不相等的点的直接映射和逆映射。

图1 二维空间及其等效一阶希尔伯特曲线Fig.1 Two-dimensional space and its equivalent first order Hilbert curve
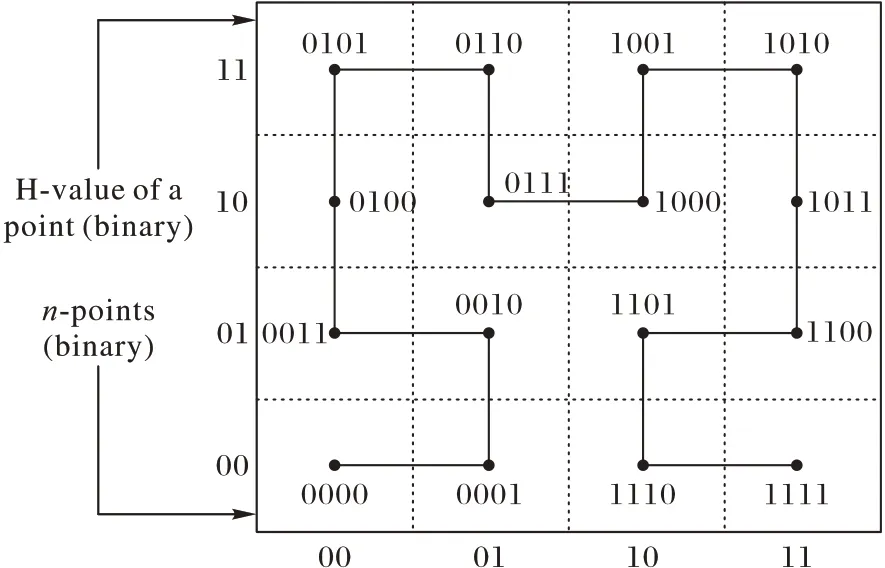
图2 二维二阶Hilbert曲线Fig.2 Two-dimensional second-order Hilbert curve
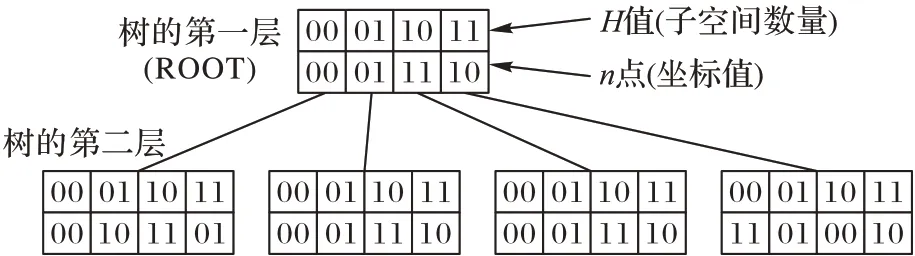
图3 二维二阶Hilbert曲线的树表示Fig.3 Tree representation of two-dimensional second order Hilbert curve
1.2 P-Grid
P-Grid[16]是一种基于分布式散列表的可伸缩自组织结构化覆盖网络,它的访问结构是基于虚拟二叉树的。二叉树结构用于为精确匹配和范围查询实现基于前缀的路由策略。P-Grid 为每个节点n 分配一个二进制位串,表示其在整个字典树中的位置,称为节点的路径(n),该路径包含从叶子到根的序列。图4 为P-Grid 二叉树的示意图。存储一个数据项,P-Grid 使用保哈希函数将数据项的标识符转换成一个二进制关键key(key ∈[0,1])。数据项被路由到该节点的路径与key最长公共前缀。例如,图4 中节点2 的路径为01,因此它存储了所有键值以01开头的数据项。

图4 P-Grid字典树示例Fig.4 Example of P-Grid trie
P-Grid 采用一种完全分散并行的构造算法,可以构造出延时较短的覆盖网络。构建过程严格基于本地对等交互,这种交互是通过在已有的非结构化覆盖网络上发起随机遍历来完成的。P-Grid 中的每个节点都维护一个路由表,该表存储关于网络中其他节点的路径的信息。具体地说,对于每个位置,它维护至少一个节点的地址,而且该节点的路径在该位置上具有相反的位。该信息以[path(n),FQDN(n)]的形式存储在路由表中,其中FQDN(n)是节点的全限定域名。具体构造算法见文献[17]。
2 New-grid数据分布和索引框架
New-grid 索引框架由从云端租用的无共享节点集群组成。New-grid 的主要目标是通过一个真正分散的P2P 架构来支持LBS,该架构可以相应地进行扩展。New-grid通过采用简单的两层架构来实现。上层是基于P-Grid 的覆盖网络,该网络负责路由查询并为计算节点分配子空间,而下层则根据数据模型的类型使用底层键值存储(HBase)来维护数据。Newgrid 中的节点有两个用途:一个节点是P-Grid 中的节点,因为它维护其路由表中所有其他节点的子空间信息;另一个节点是HBase 集群的一部分,它存储实际数据。New-grid 的体系结构将查询处理分为两个阶段:在第一阶段中,通过搜索路由表来确定存储子空间的节点。路由表包含所有其他节点的引用,这是通过将节点安排在一个虚拟二进制树结构中来实现的。在第二阶段,查询被转发到本地处理它的负责节点上。
New-grid 系统架构如图5 所示。本文使用自底向上的方法构造New-grid,其中节点首先被安排在HBase 集群中,然后加入覆盖网络。建设是在一个离线的过程中完成,并有一个小的一次性设置成本。数据插入可以在任何节点上完成。为了插入数据,首先计算多维点的H值,并根据给出的数据模型进行插入,底层使用Apache HBase[5]来存储多维点的H 值,将其用作唯一的行键。
2.1 数据插入和点查询
数据插入和点查询可以通过使用P-Grid的搜索机制来执行,将插入或查询请求转发到负责节点。本文的算法(算法1和算法2)利用键值存储提供直接数据访问的能力,各自高效地插入数据和处理点查询。在算法1 中,插入一个点,首先计算该点(第1)行)的二进制H 值(rowkey)。然后,对于每个节点模型的表,插入操作分为两个阶段:在第一阶段,搜索路由表ρ,找到名称为(FQDN)节点的路径的最长公共前缀行键(第2)行)。此模型将数据存储在一个表中,该表的名称设置为节点的名称,此步骤足以找到负责存储该点的表的名称。在第二阶段,按照标准的insert 操作在表中插入rowkey(第3)行),对于表共享模型,可以很容易地在预定义的共享表中插入rowkey(第5)行)。
Algorithm 1:Data Insert(point p,value v)
1) rowkey←compute H-value(p)
//Table per Node//
2) n.Table=PrefixMatchingBinarySearch(ρ,rowkey)
3) n.Table.insert(rowkey,value v)
4) return true
//Table Share//
5) sharedTable.insert(rowkey,value v)
6) return true
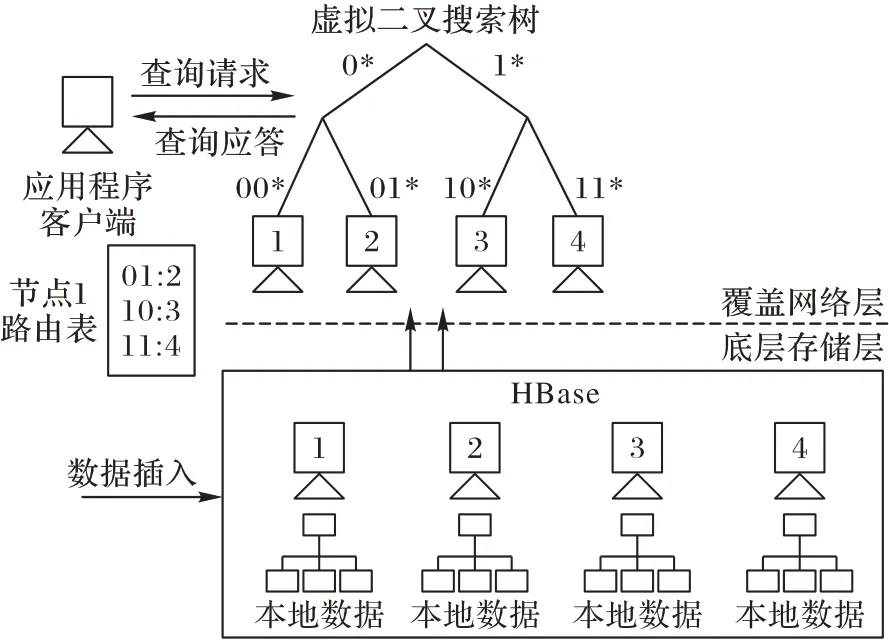
图5 New-grid系统架构Fig.5 New-grid system architecture
算法2 是查询处理算法,对于每个节点模型的表,查询处理分为两个阶段。给定d 维点p=(p1,p2,…),点查询策略试图识别与p 关联的值v。为了处理查询,首先计算该点的H 值来计算行键(第1)行)。在第一阶段,搜索路由表ρ,找到名称为(FQDN)的节点,这个节点路径与rowkey是最长的公共前缀(第2)行)。在第二个阶段,通过检索到v,在表上实现键查找操作。
Algorithm 2:Point Query Processing(p)
Input:query point p
Output:value v associated with p
1) rowkey←compute H-value(p)
//Table per Node//
2) n.Table=PrefixMatchingBinarySearch(ρ,rowkey)
3) return(v←lookup(rowkey,n.Table))
//Table Share//
4) return(v←lookup(rowkey,sharedTable))
2.2 范围查询处理
范围查询是检索某个属性位于上下边界之间的所有记录的查询类型,在形式上分为两种类型。范围查询是由上下边界坐标(l1,l2,…,ln)和(u1,u2,…,un)构成的超矩形区域,其中min ≤li≤ui≤max。LBS 中的另一个形式是“获取z 半径内(x经度,y纬度)附近的所有值”。P-Grid基于二叉树的分区将线性化后的空间划分为大小相等的子空间,并根据节点的路径将子空间分配给节点。范围查询区域与一个或多个子空间相交。一个简单的范围查询策略将通过在查询下限和上限相交的子空间之间搜索来检索查询区域中包含的所有点。本文算法将范围查询处理分为以下两个阶段:
1)在第一阶段中,将原始的范围查询划分为更小的子查询,每个子查询区域与之相交的子空间都有一个子查询,通过计算查询区域内每个子空间中点的最小H值来实现。将该点称为下一个匹配点,并将其计算为calculate-next-match()的函数。
2)在第二阶段中,根据P-Grid 的搜索机制处理每个子查询,该搜索机制将子查询转发给路径与子查询的上下界相交的所有节点。
例如,考虑图6 所示的范围查询Q1。它的下界和上界坐标是A(01,01)和F(11,10)。等效H 值范围这个查询的值是[0010,1011]。二进制树将空间划分为大小相等的四个象限,即00、01、10 和11。要搜索的第一个子空间由下界H 值确定,下界H 值为00。为了得到范围查询中包含的点,需要搜索位于上下子空间之间的所有后续子空间。例如,简单查询策略将搜索00、01 和10 个子空间。子空间11 虽然与查询相交,但是将被跳过。
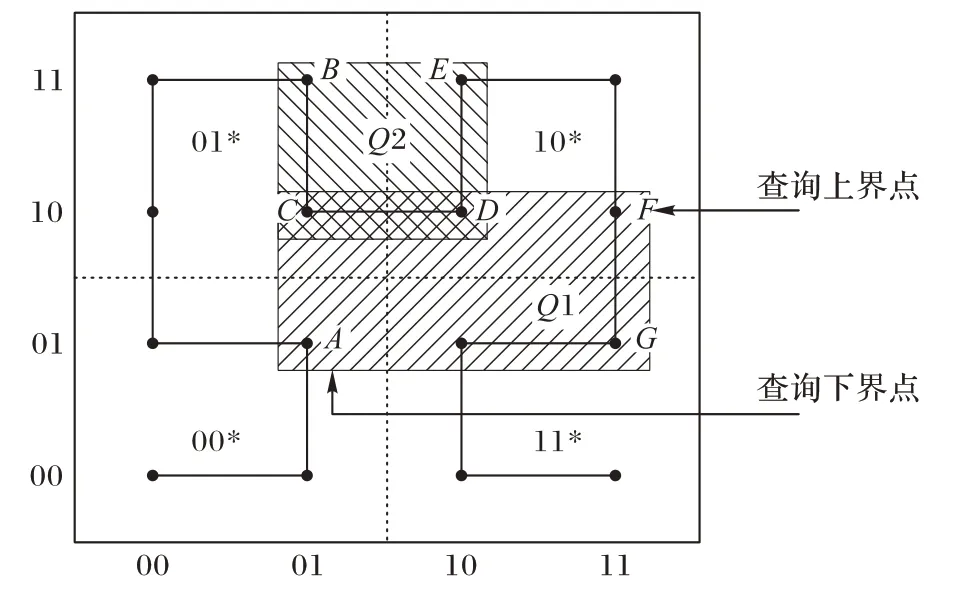
图6 映射到二维Hilbert曲线的二阶点的范围查询示例Fig.6 Example of a range query on points mapped to two-dimensional second order Hilbert curve
该算法迭代地确定在树的任意节点上与当前查询区域相交的最小子空间。在每次迭代中,将丢弃一半的子空间,并沿着树的正确分支下行,直到在叶级找到下一个匹配。同样,这种下降是一个迭代过程,在每次迭代中,都用搜索子空间的边界来限制用户定义的搜索空间。
Algorithm 3:Range Query Processing
Input:query lower point ql,query higher point qh
Output:result set Rq
1) Rq←∅
2) Sr←∅
3) Hl←compute
4) Hh←compute H-value(qh)
5) Sr←calculateSubRanges
6) for each s ∈Srdo
7) Rq←PGrid.Search(s)
8) end for each
9) return Rq
2.3 KNN查询处理
在一个d 维空间S,给定一组点N,根据一个距离函数,查询处理算法返回一组k ∈N 的点,这些点邻近于q。由于之前的结构对节点间的数据分布是不可伸缩的,而且基于MapReduce 框架对大量数据进行KNN 查询的解决方案会导致很高的查询延迟。为了缓解这些问题,提出了一个简单的查询处理策略。KNN 查询处理算法以递增的搜索区域迭代执行范围搜索,直到检索到k 个点为止。算法4 给出了KNN查询算法的步骤。在第2)行中,首先构造一个范围r,集中在查询点和初始半径δ=Dk/k,Dk表示查询点q 和它的K 最近邻点的估计距离。Dk可以用式(1)[18]估计:
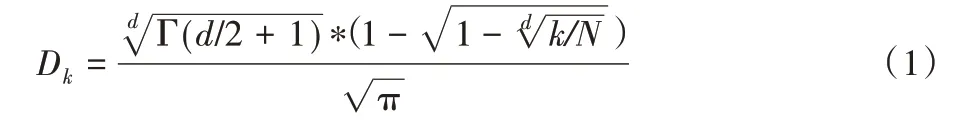
其中:Γ(x+1)=xΓ(x),Γ(1)=1,Γ(1/2)=π/2,d 是维度,N 是基数。
Algorithm 4:K Nearest Neighbors(q,k)
Input:query point q,number of nearest neighbors k
Output:k nearest neighbors
1) Qresult←∅
2) δ ←estimateRadius(k)
3) r ←δ
4) while true do
5) ql←q-r
6) qh←q+r
7) Qresult←RangeSearch
8) if|Qresult|≥k then
9) return top k results of Qresult
10) else
11) r ←r+δ
12) end if
13)end while
3 性能分析
在Amazon EC2 上实现了New-grid,集群大小为4、8 和16个节点。每个节点都是EC2 的一个中型实例,由4 个虚拟内核、15.7 GB 内存、配置为1 TB 硬盘和Centos 6.4 OS 组成;节点通过1 GB 的网络链路连接。数据存储层使用Hadoop 1.2.1和HBase 0.94.10实现。点、范围和KNN查询的实验是在一个包含4 亿个点的合成数据集上进行的。该数据集是使用基于网络的移动对象生成器生成的,该生成器模拟了旧金山湾区地图上40 000 个对象的移动。每个对象移动10 000步,并在连续的时间戳上报告其位置(经度、纬度)。该数据集遵循一个倾斜分布,因为模拟器使用真实世界的公路网。本文运行一个简单的MapReduce(MR)作业来计算数据集中点的最小值和最大值(区域边界),并根据这些点的H 值的公共前缀设置节点的路径。这有助于通过匹配预定义的子空间,使用行键在节点之间高效地分布数据集。行键将使用匹配的预定义子空间插入到正确的节点中。
在二维和三维数据集上进行了大量的实验,以证明Newgrid的TPN和TS数据模型的有效性。以没有覆盖层的Hilbert曲线(H 阶)作为索引层实现为基线。还针对MD-HBase[19]索引方案的TPB(MDH-TPB)和TS(MDH-TS)数据模型评估了New-grid 的性能。此外,还将范围查询的性能与MapReduce进行了比较。
3.1 插入的性能
LBS 不断增长的趋势,使其对可伸缩性的需求越来越明显。使用YCSB[20]基准测试工具评估了New-grid的可伸缩性。图7 将插入吞吐量的性能描述为包含4、8 和16 个节点的集群上的系统负载的函数。将工作负载生成器的数量从2 变化到96,其中每个工作负载根据Zipfian 分发版每秒生成10 000 个插入。在不同的节点上同时运行工作负载生成器并聚合结果。对于TS 模型,根据HBase 提供的水平可伸缩性,插入吞吐量几乎随工作负载生成器数量的增加而线性增长;但是,TPN 模型的插入吞吐量会随着插入趋势先增大后减小。对于位置更新60 s的间隔,TS模型达到峰值吞吐量约每秒840 000插入;然而,TPN 模型达到一个峰值吞吐量约每秒660 000 插入。两种设计的性能都超过了MD-HBase,并且随着节点数量的增加,差距也越来越大。
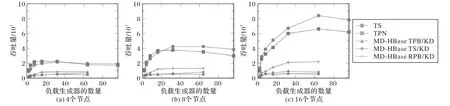
图7 更改工作负载生成器数量的效果Fig.7 Effect of varying the number of workload generators
3.2 点查询和范围查询的性能
多维点查询和范围查询是LBS 中最常见的查询。Newgrid通过直接查询HBase表来处理点查询。另一方面,范围查询的处理方法是首先将其划分为多个子查询,然后使用覆盖层将每个子查询同时转发到负责节点。图8 显示了改变节点数量会对TPN、TS和H阶模型的三维点查询性能产生的影响。当增加节点数量时,所有模型的平均响应时间都增加了,尤其是TPN 模型。TS 和H 阶模型的响应时间相同,因为它们都使用相同的查询策略;但是,TPN 模型的响应时间比其他模型要长,这是因为需要通过搜索路由表并找到相关节点的成本较高。
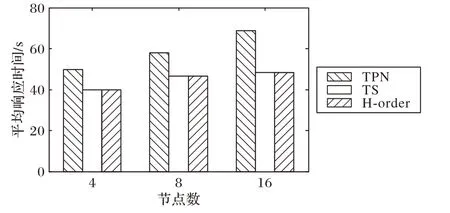
图8 点查询性能(D=3)Fig.8 Performance of point query(D=3)
图9 和图10 分别显示了不同选择性和节点数量的TPN、TS、H 阶和MR 模型的二维范围查询的性能。随着节点数量的增加,TPN、TS 和H 阶模型的查询响应时间几乎线性增加(图9);相反,MR 在对数据集进行全扫描以执行查询时,其响应时间是恒定的,因此其响应时间与选择性无关。TS 和TPN模型的性能优于其他模型,特别是对于选择性较大的查询,由于搜索区域较大的范围查询将与更多的子空间相交,从而产生多个子查询。从图10 中可以看出增加节点数量和同时保持10%的选择性对平均范围查询响应时间的影响。随着节点数量的增加,平均查询响应时间会减少,因为节点数量的增加会导致数据的有效分布。此外,TPN 模型的性能优于TS 模型,因为TPN 模型将所有数据本地存储在节点上,而TS 模型将数据分布在集群中。
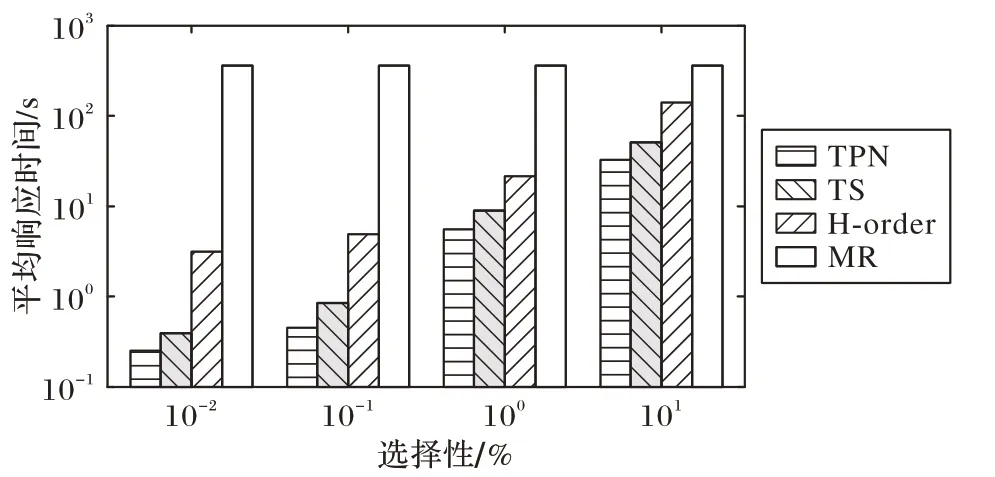
图9 范围查询的性能(节点数为4,D=2)Fig.9 Performance of range query(number of nodes is 4,D=2)

图10 范围查询的性能(选择性=10%,D=2)Fig.10 Performance of range query(selectivity=10%,D=2)
在三维数据集上进行实验的结果如图11 和图12 所示。图11显示了在4个节点集群上作为选择性函数三维范围查询的性能。当增加选择性时,TPN 和TS 模型的平均查询响应时间会增加。在本实验中,除了H 阶模型和MR 模型外,还将TPN 和TS 模型的结果与MD-HBase 的TPB 和TS 数据模型进行了比较。比较结果表明,即使在选择性较大的情况下,TPN和TS 模型的性能也较好。这是因为,在MD-HBase 中使用额外的索引层来修剪结果集,而在本文的方案中没有这样的开销。
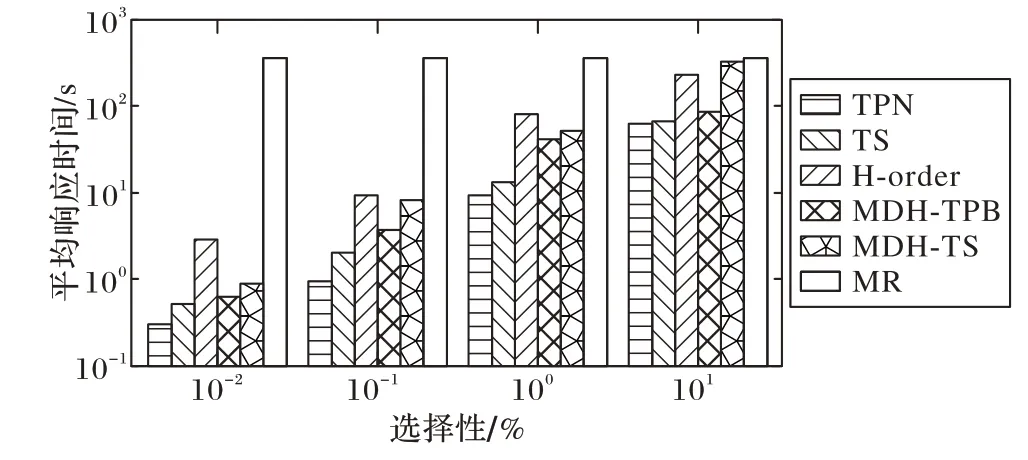
图11 范围查询的性能(节点数为4,D=3)Fig.11 Performance of range query(number of nodes is 4,D=3)

图12 范围查询的性能(选择性=10%,D=3)Fig.12 Performance of range query(selectivity=10%,D=3)
3.3 KNN查询的性能
New-grid 迭代处理k 个最近邻居(KNN)查询。首先利用式(1)估计查询点与其第k 个近邻之间的距离,即初始搜索半径;然后,执行范围搜索来检索k个结果,如果k个结果没有返回,通过增加搜索空间并再次执行范围搜索。图13 显示了通过在4 个节点集群中将k 的值从1 增加到10 000,KNN 查询在2 维数据集上对TPN、TS 和H 阶模型的性能。可以看出,随着k值的增加,所有模型的KNN 查询平均响应时间都在增加,因为随着k值的增加,查询空间也在增加。
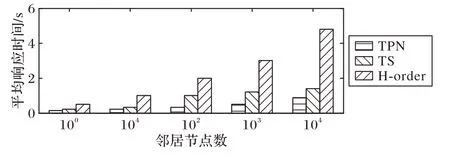
图13 KNN查询的性能(节点数为4,D=2)Fig.13 Performance of KNN query(number of nodes is 4,D=2)
当然,这种平均响应时间的增加并不是指数级的,因为具有更大搜索空间的范围查询会使用更多的节点进行处理。将k 的值设置为10 000,节点数量从4 增加到16,得到的结果如图14 所示。实验结果表明,随着集群中节点数量的增加,平均查询响应时间会降低,因为更大的范围查询会与更多的子空间相交,从而涉及到更多的节点。在这两个实验中,TPN 和TS 模型的性能都比H 阶设计的性能提高了4 到5 倍。在三维数据集上进行的一组实验的结果如图15 和图16 所示。图15显示了参数k 的变化对4 个节点簇的影响,与MD-HBase 和H阶设计进行对比,可以看出TPN 和TS模型的平均响应时间随着参数k的增大而增大。然而,与二维相比,三维KNN查询需要更多的时间来处理,因为执行范围查询的复杂性随着维数的增加而增加。

图14 KNN查询性能(k=10 000,D=2)Fig.14 Performance of KNN query(k=10 000,D=2)

图15 KNN查询的性能(节点数为4,D=3)Fig.15 Performance of KNN query(number of nodes is 4,D=3)
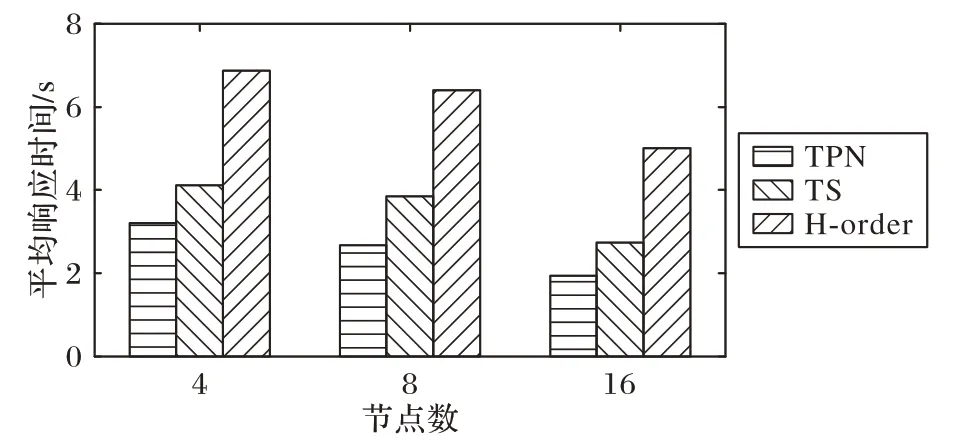
图16 KNN查询性能(k=10 000,D=3)Fig.16 Performance of KNN query(k=10 000,D=3)
4 结语
本文提出并评估了一个面向云平台上位置感知服务的多维数据分布和索引框架New-grid。New-grid是一个可伸缩的、完全分散的、独立于平台的索引框架,可以有效地处理点、范围和KNN 查询。New-grid首先在修改后的P-Grid覆盖网络中安排从云租用的节点,该网络实际上以二叉树结构划分整个空间。其次,为了有效地存储和检索多维数据,利用基于Hilbert空间填充曲线的线性化技术将多维数据转换为一维二进制键。这种技术允许我们根据对等点的路径将键映射到它们,同时保留数据局部性。我们还设计并开发了算法来动态处理范围和KNN 查询,从而消除了创建和维护单独索引表的限制。在Amazon EC2 上使用4、8 和16 个普通节点的集群进行了广泛的实验,结果表明,New-grid 的性能相比MD-Hbase更优。
在未来,我们希望通过提供以动态方式处理数据偏斜度的能力来扩展该框架,并支持更广泛的多维查询,包括skyline和spatial-join;还希望开发高效的子空间分裂算法来实现负载均衡,并开发高效的数据复制算法来提高New-grid 的容错能力;同时还想评估P-Ring P2P网络[21],看看它是否能够满足我们模型的所有要求,或者如何进行相应的修改,以及它与P-Grid在性能上的比较。

